联合调参随机共振在流量计测试中的应用
2014-08-22张莹赵歌王太勇
张莹 赵歌 王太勇
(1中国民航大学航空工程学院 天津 300300 2国家电网天津市电力公司 天津 300010 3天津大学机械工程学院 天津 300072)
联合调参随机共振在流量计测试中的应用
张莹1赵歌2王太勇3
(1中国民航大学航空工程学院 天津 300300 2国家电网天津市电力公司 天津 300010 3天津大学机械工程学院 天津 300072)
改变噪声、双稳系统或输入信号的特征参数可以在新的系统协同下诱发随机共振,统称为广义调参随机共振。对于工程中的大参数信号,噪声强度不易增减,联合调节二次采样频率和系统参数可促进系统行为的有序化。在恰当的频率尺度下,这一技术可实现对归一化后新频率与最优噪声量的均衡,产生类似绝热近似条件下的双稳随机共振现象。流量计系统的振动测试,验证了联合调参随机共振在提取噪声背景下微弱信息时的实用性和有效性。
双稳随机共振;噪声;联合调参;振动测试
1 引言
随机共振由Benzi等人[1]在研究古气象冰川演化问题时首次提出,解释了噪声在某些特定非线性系统中的积极作用。在信号处理领域,双稳系统作为一种典型的非线性系统,在与噪声作用的过程中增强了原本被噪声湮没的有效信息[2]。在经典的双稳随机共振理论中,对输入信号幅值、频率以及噪声强度的小参数限制[2],阻碍了随机共振技术在工程中的应用和推广。
针对工程中的非小参数信号,噪声调谐[3]、系统参数调节[4]和二次采样随机共振[5]分别通过改变噪声、双稳系统和信号频率的特性,以实现系统输出的最优化。基于上述三种方法各自的特点和应用,本文提出联合调参随机共振理论。该方法在流量计系统振动测试中的成功应用,验证了其更为普遍的推广意义。
2 联合调参随机共振
双稳系统作为一种非线性信号处理器[2],可表示为
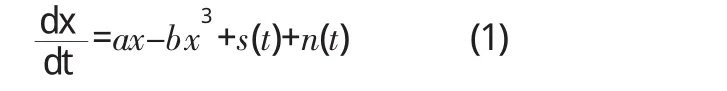
其中,系统参数a>0,b>0。s(t)为输入信号,为噪声,其强度为。研究发现[3-5],作为随机共振三要素的噪声、双稳系统和驱动信号,其特征参数的变化直接影响到双稳系统的输出结果。这三组参数可看作随机共振的广义参数,相对应的三种参数调节方法可统称为广义调参随机共振。
从实现方式上看,广义调参随机共振可看作是改变某一要素,使之与另外两要素协同作用,以达到随机共振最佳状态的过程。从微观层次来看,双稳随机共振可以用粒子在双稳势阱中的运动过程进行描述[2]。当粒子在双稳势阱中的平均跃迁频率(Kramers逃逸速率的一半)恰好等于周期驱动力的频率[6],随机共振发生,此时满足

上式中等号的成立可以双向实现。由于Kramers逃逸速率与参数a、b和D有关,系统参数调节、噪声调谐随机共振可视作改变等式右边的数值,使之趋近信号频率的过程。同时,二次采样随机共振实现了对f0的缩放,从而完成式(2)由左向右的逼近。
对实际采样信号,噪声强度D不能任意增减,由于系统参数b和噪声强度D在系统输出的建设过程中具有相同的贡献[2],可认为噪声调谐随机共振在某种程度上等同于参数调节随机共振。因此本文重点讨论系统参数调节和二次采样随机共振。这两种方法分别就噪声强度和信号频率处于大参数域时的随机共振问题提出了解决思路。
如果上述两广义参数均突破了小参数的限制,则仅靠某一种调参方法不能诱发随机共振。对此,可以首先根据预估的噪声强度进行二次采样随机共振,在噪声能量集中的低频区域对频率信息进行增强;然后调节双稳系统参数,寻找归一化后新频率产生共振所需要的噪声量,最终实现新双稳系统、新频率和原噪声强度的最佳匹配。该处理过程如图1所示,本文定义为联合调参随机共振,并通过工程实例进行说明。
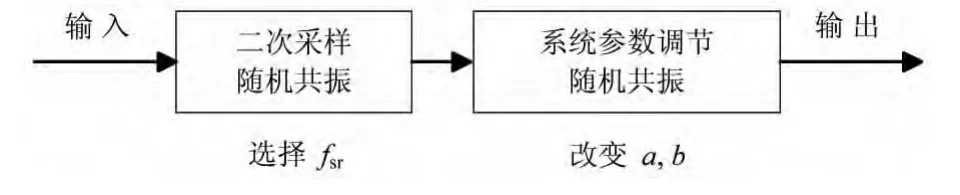
图1 联合调参随机共振的处理过程
3 流量计系统的振动测试
3.1 工程背景
实例中采样数据来自于对某日用品公司流量计系统的振动测试,其测试目的在于寻找导致流量计出现异常跳动的主要原因。图2为现场测试照片。图3给出了流量计系统的结构简图,该系统主要由齿轮泵、管道、支架和流量计组成。

图3 流量计系统结构简图
测试前,通过读取设备的特征数据确定各自的工作频率:齿轮泵驱动电机工作频率为24Hz(额定转速为1400r/min),齿轮泵工作频率为8Hz(额定转速为480r/min),流量计振动频率为105Hz。振动数据通过在所选测点布置加速度传感器进行拾取,并送入振动测试系统进行后续的显示、存储和分析。
3.2 联合调参随机共振的应用
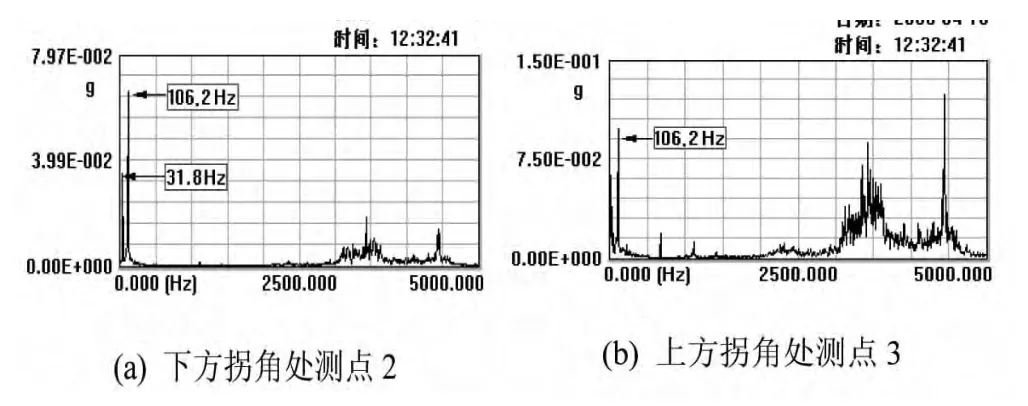
图4 正常工作时,采样信号的幅值谱
科技论文与案例交流
现场发现,流量计系统管道上方拐角处的振感强烈,据此选择测点3为研究对象,传感器垂直向下固定在管道外壁。同时,在与之对应的下方测点2处采集垂直方向的加速度信号进行对照。测试参数如下:采样点数4096,采样频率12800Hz,FFT谱线条数800,平均次数5。由测试系统得到两测点的振动加速度幅值谱如图4所示。此时系统为正常运行状态,即流量计和齿轮泵开启,管道内加载液体。
比较上面两图,图4(a)中测点2处振动信号中包含的频率成分较少,估计噪声强度得到。由谱图可以读取特征频率31.8Hz和106.2Hz。分析可知,106.2Hz对应流量计振动频率,31.8Hz为电机频率被齿轮泵频率调制后的上边带频率。
在振动明显的管道上方,测点3处的振动频谱结构较复杂,同时幅值也高于测点2。通过估计噪声强度,得到。由于图4(b)中,中高频区域具有突出的谱峰群,不能直接对特征频率进行判定。
为突出低频信息,采用联合调参随机共振的方法处理测点3的采样数据,选择二次采样频率Hz,系统参数,,得到图5所示的输出结果,其中图5(b)放大了0~500Hz的低频区域。
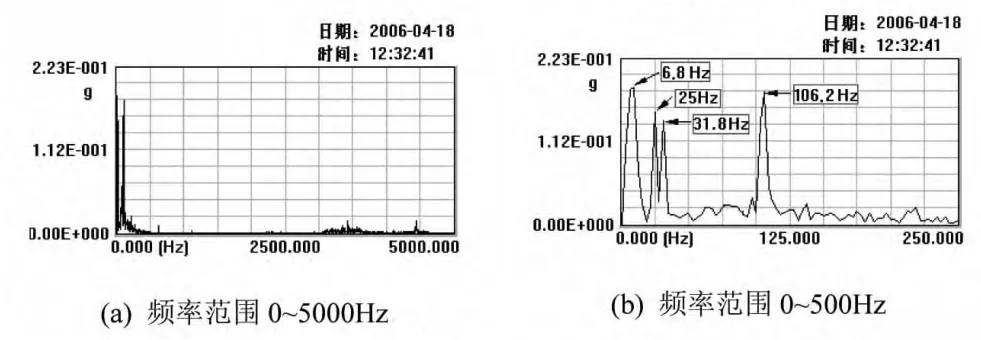
图5 正常工作时,测点3处随机共振输出的幅值谱
对照图4(b),图5(a)由于随机共振的发生增强了原始信号的低频能量,同时中高频干扰成分被压低。从拉开的低频谱图可以看出,在 6.8Hz、25Hz、31.8Hz、106.2Hz处都有比较明显的谱峰,可确定为测点3振动信号的特征频率。其中6.8Hz和25Hz分别对应齿轮泵和驱动电机的工作频率,而31.8Hz和106.2Hz也是由信号调制引起,解释同前。这一分析结果与实际工况相符,可排除其他外在因素对流量计正常工作的影响,因此考虑异常跳动由系统本身结构引起。
由于管道上方较下方振动显著,而观察流量计系统的结构发现,测点2附近的管道与地基有连接,这一支撑约束增强了该部分结构的抗干扰性,因此得到图4(a)中幅值较小,且其频率成分相对简单的谱图;而支架距离较远的测点3,则呈现出复杂而强烈的振动现象。为此,再次测试同一工况下流量计上测点1的振动情况,得到了与测点3类似的分析结果。
由此可知,管道上方拐角处的振动对流量计产生了较大的影响,从而成为导致流量计异常跳动的主因。综合考虑系统结构特点,建议对上方拐角进一步加固。
4 结语
在广义调参随机共振的定义下,本文将联合调参随机共振的方法应用于流量计振动测试的分析过程。对于工程信号,如果仅调节系统参数或二次采样频率不能达到随机共振状态,可以联合调节两组参数构建新的系统输出,具体操作时,二次采样随机共振先于双稳系统参数的调节。研究表明,相比传统随机共振,联合调参随机共振在噪声背景和信号频率方面具有更强的适应性。
[1]BenziR.,Alfonso S.,VulpianiA.Themechanism ofstochastic resonance[J].J.Phys.A,1981,14:L453-457.
[2]Gammaitoni L.,H?nggi P.,Jung P.,et al.Stochastic Resonance[J].Rev.Mod.Phys.,1998,70(1):223-285.
[3]Xu B.H.,Duan F.B.,Chapeau-Blondeau F.Comparison of aperiodic stochastic resonance in a bistable system by adding noise and by tuning system parameters in signal transmission[J].Phys.Rev.E,2004,69:061110.
[4]Xu B.H.,Li J.L.,Zheng J.Y..How to tune the system parameters to realize stochastic resonance[J].J.Phys.A:Math.Gen.,2003,36:11969-11980.
[5]冷永刚,王太勇,秦旭达,等.二次采样随机共振频谱研究与应用初探[J].物理学报,2004,53(3):717-723.
[6]冷永刚.基于Kramers逃逸速率的调参随机共振机理[J].物理学报,2009,58(8):5184-5188.
张莹(1983—),女,博士,讲师,研究方向为随机共振技术、航空发动机的故障诊断与健康管理等。
中国民航大学科研启动基金2010QD07S
