多卫星导航系统精密单点定位精度分析
2014-08-22付青
付 青
(武汉大学遥感信息工程学院,湖北 武汉 430079)
0 引 言
精密单点定位(PPP)是利用精密卫星轨道产品和高精度的误差模型消除GNSS接收机观测误差,并采用最小二乘平差或滤波推估方法,实现单台GNSS接收机的高精度定位技术[1]。PPP技术具有全天候、无需参考站和高精度定位的优点,一直为科研项目和民用工程提供高可靠、高精度的保障,譬如准实时GPS的气象研究、地壳形变研究等[2-3]。但其必须有一个较长时间的收敛过程才能得到高精度稳定解,正是该特点阻碍它在很多领域的进一步发展。
随着全球GNSS系统的不断完善,特别是北斗卫星导航系统于2012年12月27日正式服务亚太地区,研究GNSS组合定位再次成为很多学者的研究热点。截止目前为止,BDS的在轨工作卫星由5 GEO卫星+5 IGSO卫星+4 MEO卫星组成。现在对BDS关注热点集中在单系统PPP定位精度、BDS与GPS组合定位精度和BDS与GPS、GLONASS三星组合定位精度等方面。YANG[4]等分析了BDS公众用户的可视卫星数及其几何精度值(DOP)。施闯[5]等利用武汉大学GNSS中心提供的精密星历和精密钟差产品解算得到BDS静态PPP达到cm级,动态RTK可以达到5~10 cm.李伟[6]等分析了GPS单系统、BDS单系统、GPS与BDS组合系统三种定位模式,使用三个站两天的观测数据实验,得出GPS与BDS组合定位系统的收敛时间相比单系统明显减少,而在单系统本身卫星星座分布良好时,组合定位系统定位精度提高不大。这些实验都在单BDS系统或者BDS与GPS双星组合系统进行,对于BDS与GPS、GLONASS三星组合系统研究非常少。本文旨在分析三星组合系统的收敛时间变化以及其定位精度。由于多星组合系统必须在一定的时间和坐标系统进行,为此,本文统一了三星组合定位的时间系统和空间系统,利用武汉九峰站全天观测数据进行实验,验证三星组合定位能有效缩短PPP收敛时间以及提高在单GNSS系统卫星数较少或者卫星星座分布较差时的定位精度。
1 时空基准统一
1.1 时间基准统一
GPS的时间系统属于原子时系统,它的秒长和原子时秒长相同,但它和国际原子时存在着不同的原点,并且在任一时刻它们二者之间都存在一个常量偏差(19 s)。
北斗系统的时间基准为北斗时(BDT)。BDT采用国际单位制(SI)秒为基本单位连续累计,不闰秒,起始历元为2006年1月1日协调世界时(UTC)00时00分00秒,采用周和周内秒计数。BDT与UTC 之间的闰秒信息在导航电文中传播[7]。
GLONASS时间系统(GLONASST)属于UTC时间系统,它是基于GLONASS同步中心(CS)时间产生的,由于GLONASS控制部分本身存在的特性,使得GLONASST与俄罗斯维持的协调世界时UTC(SU)存在的整数差为3 h,此外它们之间还存在有1 ms 以内的系统误差τr[8].
三类卫星的时间系统详细描述如表1所示。
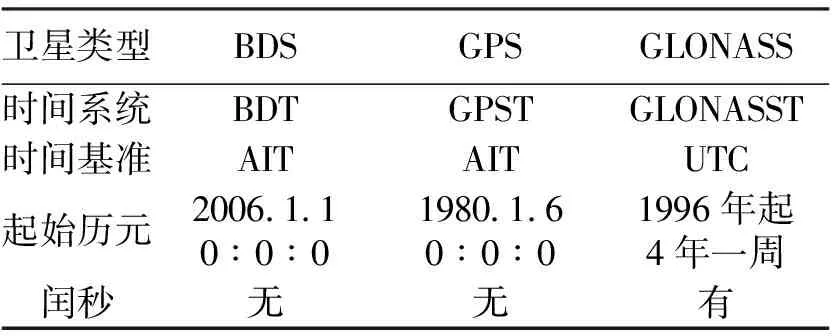
表1 三类卫星时间系统的比较
1.2 坐标基准统一
GPS坐标系统采用的是WGS-84坐标系。该坐标系是地心空间直角坐标系,它的原点为地球质心,Z轴指向国际时间服务机构(BIH)1984.0定义的协议地球极(CTP)方向,X轴指向BIH 1984.0的零子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系。BDS坐标系统采用的是我国2000大地坐标系统(CGCS2000),它的定义和国际地球参考系统(ITRS)相一致[7]。GLONASS坐标系统以前采用的苏联1985地心坐标系(SGS85),1993年以后改为使用PZ90.02[8-9]坐标系,该坐标系是由俄罗斯进行地面网与空间网联合平差后所建立的。WGS-84、CGCS2000和PZ90.02坐标系的参考椭球定义的基本参数如表2所示。

表2 GPS、BDS与GLONASS坐标系统参数
GPS与BDS两个坐标系的主要不同在于参考椭球的扁率f有微小的差异,而这种差异在当前的测量精度水平中可以忽略,对于在坐标系定义上的比较,可以认为在同一历元下CGCS2000和WGS-84在坐标系的实现精度范围内,两者的坐标是一致的[9]。
当前,大多数学者认为使用俄罗斯MCC计算得到的七参数作为二个坐标系转换参数的精度最高,该七参数是通过全球激光跟踪测轨数据计算得到,PZ90.02与WGS84之间的坐标转换公式[10]为
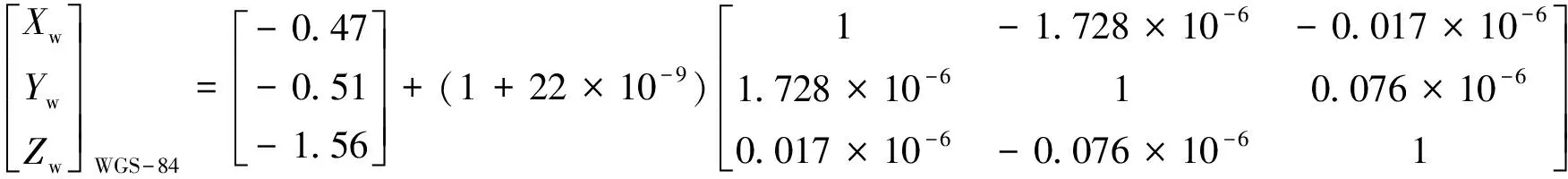
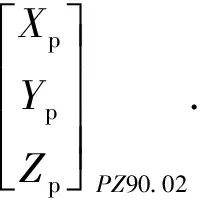
(1)
2 多星组合定位模型
2.1 原始观测量数学模型
在多卫星组合定位中,由GNSS接收机获取的伪距和载波相位观测量可以给出二者的观测方程[11]。其中,g表示GPS卫星,l表示GLONASS卫星,c表示BDS卫星。
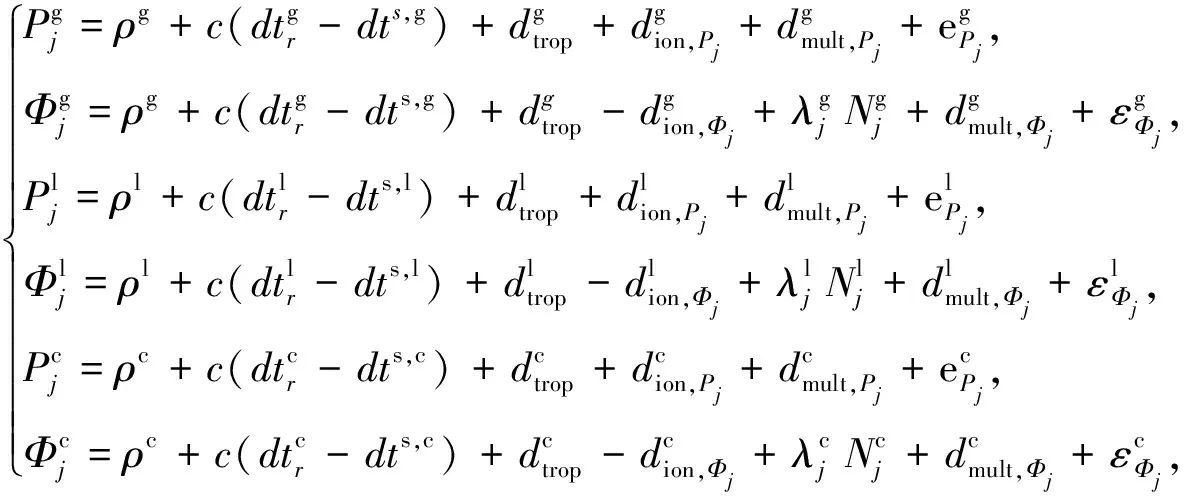
(2)
式中:下标j(=1,2)为卫星频率号;P为伪距观测量;Φ为载波相位观测量;dtr、dts分别为接收机与卫星钟差;c为光速;dtrop为对流层延迟量;dion为电离层延迟量;λ为载波波长;N为整周模糊度;ePj、εΦj分别为伪距与载波相位的观测噪声;ρ为信号发射时刻的卫星与信号接收时刻的GNSS接收机天线相位中心的几何距离。
2.2 PPP非差组合模型
通常情况,采用无电离层组合模型消除伪距与载波相位中的电离层延迟影响,其表达式为
(3)
2.3 扩展卡尔曼滤波
由于在组合定位中,观测方程是非线性的,故本文采用扩展卡尔曼滤波(EKF)[12]。其表达式为
(4)

当观测方程经过线性化后,状态量与其相关系数矩阵的时间更新为
(5)
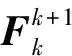
3 实验及其结果分析
实验数据来源于武汉九峰站2013年8月28日全天观测数据,该站接收机型号为TRIMBLE NETR9,它可以获取当前所有的在轨导航卫星系统的观测数据,并且设置它的观测时间为GPST,卫星高度截止角为15°.该数据采样间隔30 s,全天历元总数为2 880.对全天实测数据按照如下6种方案进行实验:①GPS单系统;②BDS单系统;③GLONASS单系统;④GPS与BDS组合双系统;⑤GPS与GLONASS组合双系统;⑥GPS、BDS与GLONASS组合三系统。
图1示出了六种方案中可视卫星数,从图1可以看出,全天时间中GLONASS可视卫星数最少,GPS可视卫星数最多,BDS处于二者之间。表3示出了6种方案中可视卫星个数情况,从该表可以看出全天时间中GPS平均可视卫星颗数7.7颗;BDS平均可视卫星数7.1颗;GLONASS平均可视卫星数6.0颗;三星组合定位的平均可视卫星颗数最高,达到20.4颗。可视卫星颗数越多,系统的定位精度亦更高。
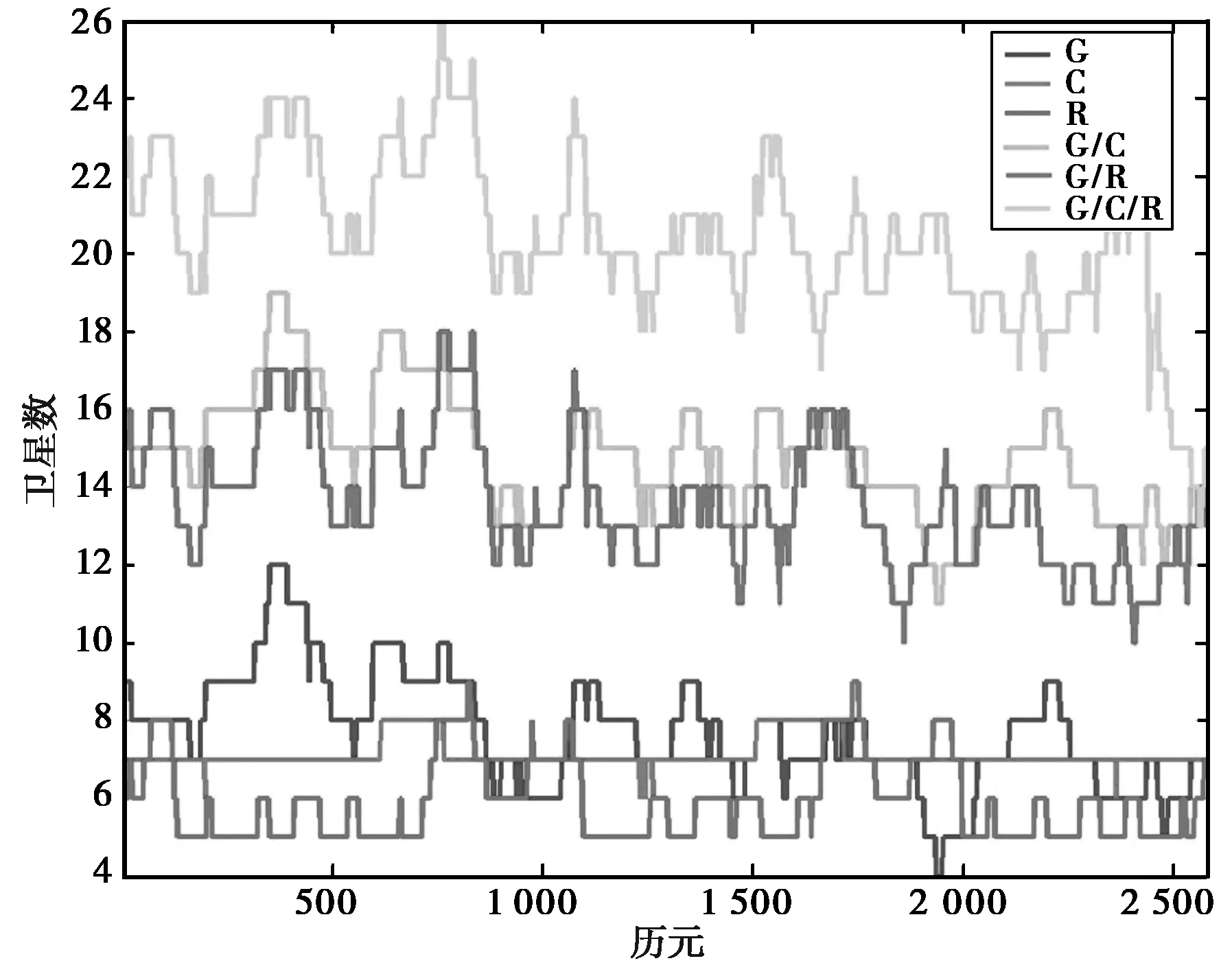
图1 可视卫星数曲线
表3可视卫星数
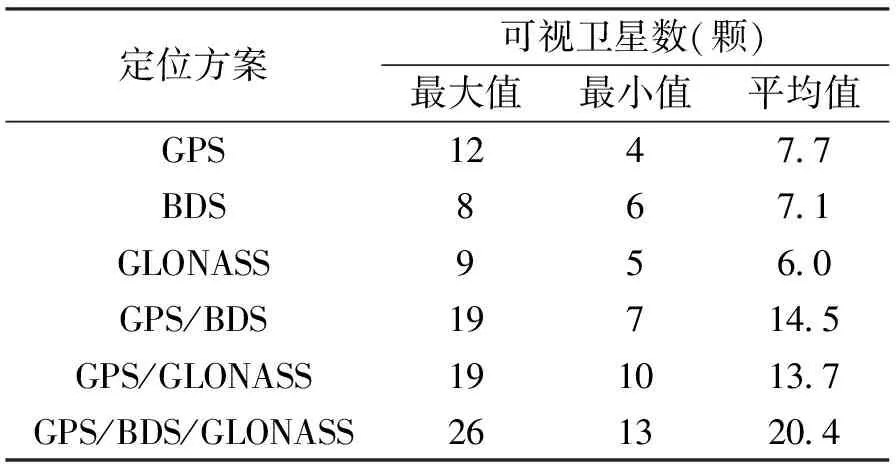
定位方案可视卫星数(颗) 最大值最小值平均值 GPS1247.7 BDS867.1 GLONASS956.0 GPS/BDS19714.5 GPS/GLONASS191013.7 GPS/BDS/GLONASS261320.4
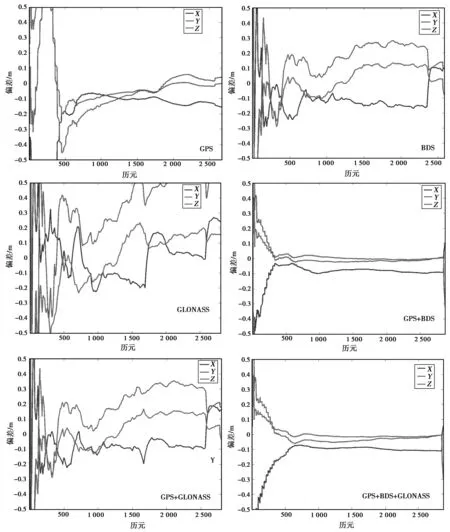
图2 6种方案X、Y、Z三个坐标偏差图
图2示出了6种方案X、Y、Z三个方向的偏差,从图2可以看出,GPS单系统定位性能较好,收敛后全天X、Y、Z三个方向都处于10 cm以内,主要是因为GPS系统建设较早,系统稳定,卫星已实现全球覆盖,星座空间分布较好。BDS单系统定位性能次之,收敛后全天X、Y、Z三个方向都处于20 cm以内,这是因为BDS系统建设正处于第二个阶段,卫星覆盖亚太地区,暂未实现全球覆盖。GLONASS单系统收敛后全天X、Y、Z三个方向处于40 cm以内,其定位精度受GLONASS卫星本身硬件延迟以及精密卫星轨道精度影响较大。从图2中还可以看出,GPS单系统收敛时间为180 min左右(采样频率30 s),BDS单系统收敛时间为200 min左右,GLONASS单系统收敛时间为240 min左右,而对于GPS与BDS组合定位的收敛时间为150 min左右,GPS,BDS和GLONASS三星组合定位的收敛时间只需要90 min左右,明显缩短单系统的收敛时间。所以,对于GPS与BDS双系统组合定位,能够有效的提高BDS单系统定位性能,有效的减少BDS单系统的收敛时间,该组合系统的定位精度优于5 cm,同样对于GLONASS与GPS组合定位,有效地提高了单GLONASS系统的定位精度。对于三星组合定位系统,与单系统比较,收敛时间最短,定位精度最高。
从表4可以看出,GPS单系统的X、Y、Z三个方向平均偏差分别为8.81 cm、6.10 cm和5.02 cm,BDS单系统的X、Y、Z三个方向平均偏差分别为8.90 cm、9.53 cm和5.39 cm,GLONASS单系统的X、Y、Z三个方向平均偏差分别为2.95 cm、18.62 cm和5.04 cm,三星组合系统的定位精度最高,X、Y、Z三个方向平均偏差分别为8.00 cm、1.40 cm和0.37 cm.三星组合定位精度的提高,主要是由于组合定位系统的空间可视卫星明显增加如表3所示,改善了单系统的卫星空间分布,尤其是在单系统出现遮挡,可视卫星较少,组合定位系统的精度要明显高于单系统。
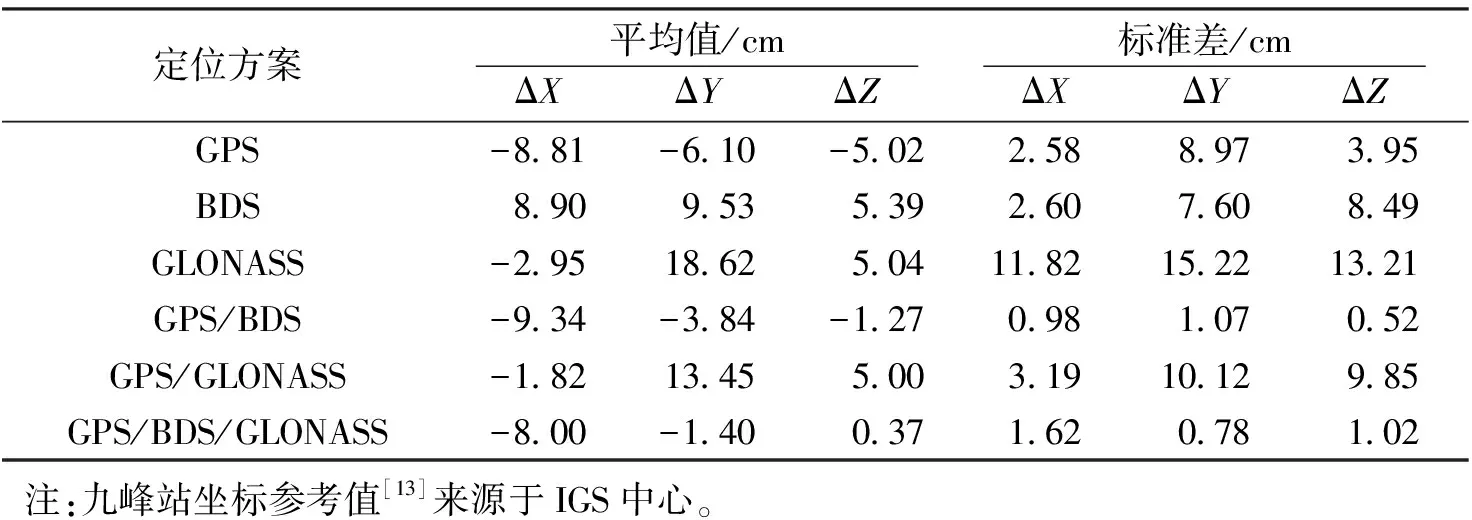
表4 统计6种方案X、Y、Z三个坐标偏差
4 结束语
随着我国北斗卫星导航系统加入GNSS行列,研究BDS与其他系统之间的组合定位尤为重要,特别是在单系统受所处环境影响导致可视卫星颗数较少时,组合系统能够有效的提高单系统的定位精度。本文在这个背景下,对BDS、GPS与GLONASS三类卫星的单系统定位、双系统组合定位以及三星组合定位6种情况进行实验分析,得到以下结论:
1)组合定位系统收敛时间相比单系统收敛时间有所减少,这对于改善单系统PPP需要长时间收敛时间具有重要意义。
2)组合定位系统能够有效的提高单系统的可视卫星颗数,改善组合系统的空间卫星分布,这也是组合定位系统能够提高单系统定位精度的前提保证。特别是在环境恶劣情况下,单系统卫星颗数较少时,组合定位系统能够发挥明显优势。同时,GNSS组合定位必将是未来定位技术的发展趋势,本文为GNSS定位提供一定的参考意义。
[1]KOUBA J,HEROUS H. Precise point positioning using IGS orbit and clock products [J]. GPS Solutions,2011,5(2):12-28.
[2]GENDT G,DICK G,REIGBER C,etal. Near real time GPS water vapor monitoring for numerical weather prediction in Germany [J]. Meteorological Society Japan,2004,82(1B):361-370.
[3]CALAIS E,HAN J Y,DEMETS C,etal. Deformation of the North American plate interior from a decade of continuous GPS measurements [J]. Geophysical Reserach,2006,111,B06402,doi:10.1029/2005JB004253.
[4]YANG Yuanxi,LI Jinlong,XU Junyi,etal. Contribution of the compass satellite navigation system to global PNT users [J]. Chinese Science Bulletin,2011,56(26):2813-2819.
[5]SHI Chung,ZHAO Qile,LI Min,etal. Precise orbit determination of Beidou satellites with precise positioning [J]. Science China: Earth Sciences,2012,55(7):1079-1086.
[6]LI Wei,TEUNISSEN P J G,ZHANG Baocheng,etal. Precise point positioning using GPS and Compass observations [C]//Proceedings of the 4th China satellite navigation conference (CSNC),Wuhan,China,15-17 May,2013.
[7]中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1 (2.0版)[R]. 2013.
[8]Russian Institute of Space Device Engineering. GLONASS interface control document(ICD)(version5.1)[R]. 2008.
[9]党亚民,成英燕,薛树强.大地坐标系统及其应用[M].北京:测绘出版社,2010.
[10]李鹤峰,党亚民,秘金钟,等.BDS与GPS、GLONASS多模整合导航定位时空统一[J].大地测量与地球动力学,2013,33(4):73-78.
[11]韩保民,欧吉坤.基于GPS非差观测值进行精密单点定位研究[J].武汉大学学报·信息科学版,2003,28(4):409-412.
[12]ARTHUR G. Applied optimal estimation [M]. The M. I. T. Press,1974.
[13]IGS. JFNG site information form international GNSS service [EB/OL].ftp://igscb.jpl.nasa.gov/pub/station/general/sitelog_instr.txt,2013.
