材料基因组计划简介

赵继成

材料基因组计划简介

赵继成

教授，美国俄亥俄州立大学材料科学与工程系，俄亥俄州 43210

材料基因组计划；材料设计；集成计算材料工程

美国总统奥巴马明确指出“材料基因组计划”(The Materials Genome Initiative, MGI) 的总目标是“将先进材料的发现、开发、制造和使用的速度提高一倍”。白宫科技政策办公室在2011年6月发布的相应的白皮书《具有全球竞争力的材料基因组计划》中阐述了材料创新基础设施的三个平台：计算工具平台、实验工具平台和数字化数据(数据库及信息学)平台。材料基因组计划/工程不仅仅是要开发快速可靠的计算方法和相应的计算程序，而且也要开发高通量的实验方法来对理论进行快速验证并为数据库提供必需的输入，还要建立普适可靠的数据库和材料信息学工具，以加速新材料的设计和使用。材料基因组计划/工程旨在材料领域建立一个新的以理论模拟和预测优先、实验验证在后的“文化”，从而取代现有的以经验和实验为主的材料研发的理念。

1 美国材料基因组计划简介

美国的“材料基因组计划”(The Materials Genome Initiative, MGI) 是白宫科技政策办公室召集国防部、能源部、商务部、国家科学基金、工程院、科学院等机构的代表组成的跨机构工作组拟定的国家性计划，由美国总统巴拉克·奥巴马于2011年6月24日在卡耐基·梅隆大学作的以“先进制造业伙伴关系”为主题的演讲中宣布。奥巴马明确地指出材料基因组计划的总目标是“将先进材料的发现、开发、制造和使用的速度提高一倍”。大约一年以后，2012年5月14日，白宫科技政策办公室和美国国家标准与技术研究院(NIST)共同召集了约170人在白宫开了一次以“促成一个全国性的运动”为目标的会议(本文作者应邀参加了这次活动)，要求广泛参与和大力促成。材料基因组计划作为一个国家性的“运动”正在美国积极地展开，想以此保持和提升美国新材料的技术优势，以促进其制造业的复兴。

白宫科技政策办公室在2011年6月24日发布的相应的白皮书《具有全球竞争力的材料基因组计划》中阐述了材料创新基础设施的三个平台：计算工具平台、实验工具平台和数字化数据(数据库及信息学)平台，如图1所示[1]。材料基因组计划提倡的并不只是开发和应用计算材料学，而是要集成计算工具、实验工具和数据库来加快材料的设计与应用。白皮书中强调材料创新基础设施是一个材料设计与制造的“加速器”。

图1 材料基因组计划中的材料创新基础设施的内涵[1]

在材料基因组计划之前，美国国防高级研究计划局 (DARPA) 曾在2000年开始资助美国通用电气公司(GE)、普惠公司(P&W)和波音公司 (Boeing) 开展了以 “加速材料应用”(Accelerated Insertion of Materials, AIM) 为题的项目。 要求这三大公司集成所能获得的模型与数据(不管是基于理论的，还是半经验的或纯经验的)来示范材料性能的优化或加工过程的优化，还要求把供应商的模型与数据也用网络连接起来用于整个优化过程。 这个项目还要求公司建立材料设计人员和产品设计师早期接触的机制。这些项目对美国材料快速设计与应用，特别是结构材料的设计与应用有长远的影响。笔者参加了在GE公司的 AIM项目，对它所产生的影响感受很深。

美国科学院和工程院共同设置的国家研究理事会 (National Research Council, NRC) 在2008年发表了题为《集成计算材料工程》(Integrated Computational Materials Engineering, ICME)的报告[2]。报告明确指出了当前材料设计的方法和系统面临的问题：①现代的计算工具已经从根本上大大缩短了新产品设计的时间，材料设计却没有相似的可靠而普适的计算工具，使材料设计主要靠试验，从而导致材料设计远远落后于新产品设计；②太长的材料设计周期和低成功率使得新材料在新产品中的使用越来越少，从而导致非最佳的材料被用在产品中；③用于产品的材料性能欠佳而成为制约产品性能设计的瓶颈，造成恶性循环。“ICME是一个新的学科，旨在把计算材料科学的工具集成为一个整体系统以加速材料的开发，改造工程设计的优化过程，并把设计和制造统一起来”，从而在实际制作之前就实现材料、制造过程和构件的计算机优化。要实现ICME必须：①把ICME作为材料科学与工程领域的一个新学科来建立从而导致教育、研究和信息共享方面的转变；②克服因材料计算工具变成广泛应用的工程工具后由于速度缓慢和缺乏训练有素的计算材料工程师而引起的工业界的不接受；③政府在ICME发展初期必须给予协调一致的支持来建立ICME工具、基础设施和教学方法[2]。

AIM项目和 ICME报告可以说是材料基因组计划的前奏。AIM项目让三个大公司和它们众多的供应商公司感觉到了ICME方法的可行性和将来可能引起的变革。ICME报告不仅对工业界有很大的影响，也把学术界和教育界的积极性调动起来了，所以，AIM项目和ICME报告为材料基因组计划的提出打下了基础。

在奥巴马提出材料基因组计划之前，美国宾夕法尼亚州立大学材料系刘梓葵教授于2002年率先注册了“材料基因组”的商业网站 ( http://www.materialsgenome.com ) 用来提倡相图计算(CALPHAD)方法及其数据库的应用。几年以后麻省理工学院 (MIT) 材料系的 Gerbrand Ceder教授开始建立材料基因组的非商业网站 ( http://www.materialsgenome.org ) 来提倡大规模快速的第一性原理计算在材料设计中的应用(主要集中在功能材料上)。直到奥巴马提出材料基因组计划之后，这个“运动”才在美国和其他国家展开。中国也在2011年12月开了一个相关的以“材料科学系统工程”为主题的香山会议[3]。

2 材料中的“基因”

严格地说，材料中并没有与生物中的基因相对应的“基因”，但是材料基因组计划与人类基因组计划还是有很强的类比性，如表1所示。人类基因中的DNA和RNA的排列(排序)决定人体的主要机能(性状)；与此类似，原子的性质和排列包括晶体结构和缺陷决定了材料的内在性能。比如，fcc和bcc结构通常比hcp结构有更好的延展性。又比如，fcc相的扩散系数通常低于bcc相扩散系数，因为fcc相是更紧密排列的。因此晶体结构(包括其中的原子)包含着材料性能的信息。人体中的大多数基因需要通过蛋白质“翻译”才能表现它们的特征；与此类似，大多数材料的性能(尤其是力学性能)需要通过微观组织(结构)去体现出它们的宏观性能(单晶应用除外)。人类基因组计划是建立DNA和RNA的排序和人体机能(性状)之间的关系；与此类似，材料基因组计划就是寻找和建立材料从原子排列到相的形成到显微组织的形成到材料宏观性能与使用寿命之间的相互关系。人类基因组和材料“基因组”之间的主要区别在于人类基因具有繁殖的信息并可以复制，这在材料中是不存在的(我们只能用相图预测不同元素融合/“结婚”在一起时会形成什么相/晶体结构)。另一个关键的不同之处在于人体基因是含有某个特征代码的最小重复单元，而材料的微观组织更加多样化，没有严格相当的“基因”(没有简单的双螺旋结构)。如果仍想寻求材料中的“基因”，我们可以调用“代表体积元(RVE)”这个概念：一个基因包含人体机能的密码；而一个RVE可以用来预测材料的宏观性能(当所有的成分－结构－性能关系都已建立之后)。我个人倾向于把原子和他们的排列(包括成分、晶体结构和缺陷)作为材料的“基因”。

总体来说，如同人的基因排列决定了人体机能一样，材料显微组织及其中的原子排列决定了材料的性能；因此，材料基因组工程就是寻找和建立材料从原子排列到相的形成到显微组织的形成到材料宏观性能与使用寿命之间的相互关系。这种把成分－结构－性能关系和数据库与计算模型结合起来就可以大大加快材料研发速度，降低材料研发的成本，提高材料设计的成功率。如何根据制造需求提出材料的性能需求，再根据性能需求来快速、准确地设计研发出所需材料是材料基因组工程的目标。在这里用材料基因组工程比用材料基因组计划更确切些。

3 计算工具

《集成计算材料工程》(ICME)报告中总结了材料计算的主要工具，可参考文献[2]。本报告将不重复描述这些工具，而是从结构和性能预测的角度介绍一些计算方法的发展。

3.1 第一性原理和分子动力学计算

通常我们讲成分－结构－性能关系是材料科学的基础，所以从成分直接预测晶体结构是最基本的，也是很重要的。近几年来开发的方法基本可以做到从成分直接预测晶体结构，特别是二元系和固定成分的化合物相的晶体结构。Ceder小组开发了把第一性原理计算与信息学(数据挖掘)相结合来预测晶体结构的方法[5-6]，其可靠性在80个二元系中得到了很好的验证[7]；Zunger和他的合作者也开发了一种预测晶体结构的基因算法[8]；中国最近开发的卡里普索(CALYPSO，Crystal Structure Analysis by Particle Swarm Optimization) 晶体结构预测方法也有很好的应用前景[9-10]；另外一种叫PEGS+DFT的方法已经被成功地用来预测复杂离子晶体的晶体结构[11-13]，这种方法最近甚至被用来成功地预测了一个非晶态化合物的局部晶体结构[14]。可以看出，最近几年从过去比较简单的用结构图(structure maps)[15-16]预测到现在更准确的晶体结构预测已有很大的进展，但是结构图在预测多组元合金中的相结构可能还是有它的用处[17]。

有了晶体结构的信息就可以用泛函理论(DFT)来计算一个晶体的很多性能，比如绝对温度(0 K)下的基态能、晶格常数、电子态密度、弹性模量等。最广泛应用的DFT计算程序是VASP(Vienna ab-initio Simulation Package)[18-19]。在多电子系统需要对DFT进行自相互作用修正[20]，强相关体系和磁性体系的计算会导致较大的误差。目前采用的对策主要包括局域密度近似结合动力学平均场 (LDA+DMFT) 方法[21-23]和局域密度近似结合Gutzwiller近似的(LDA+Gutzwiller) 变分法[24]。

对任意成分的固溶体进行DFT计算需要做些近似，以免采用过多的晶包从而导致太长的计算时间。特别是准随机结构(SQS, Special Quasirandom Structure)[25]、相干势近似(CPA,Coherent Potential Approximation)[26-27]和虚拟晶体近似(VCA, Virtual Crystal Approximation)[28-29]，是3种很有效的方法。团簇变分法(CVM，Cluster Variation Method)或集群扩展法(Cluster Expansion)也是计算固溶体性能需要常用的方法[30-34]，这种方法在一个已被广泛使用的叫ATAT(Alloy Theoretic Automated Toolkit：合金理论自动工具包)的开源程序中实施[35-39]。该程序有很强的普适性，因为它可以处理多成分、多点阵和张量化的体系，也已经包括振动(声子)和电子的贡献。计算非0 K温度的性能必须先计算声子振动的性能[40-44]。

用以上的方法可以计算0 K的形成焓和在不同温度下的Gibbs自由能、比热容、晶格常数、弹性模量、声子散射曲线、电子态密度 (从而预测能带隙)、热膨胀系数(CTE)等。从DFT计算的Gibbs自由能的误差范围大概在±(5～10) kJ/mol，所以可以用来预测不同的晶体结构(相互值的大小排序很可靠)，但是其绝对值还达不到相图计算方法(CALPHAD)所需的精度(通常要求在±(0.1～0.5) kJ/mol)。

扩散系数是动力学模拟特别是多元合金中的形核和长大过程模拟所必需的数据。第一性原理已经可以很好地计算自扩散系数[45]、杂质扩散系数[46-47]、互扩散系数[48-50]以及离子晶体中的离子扩散系数[51]。

第一性原理计算热膨胀系数并不太困难[52-53]，而且现在可以直接用ATAT程序来计算[37]。 离子晶体和共价晶体的硬度也可以用第一性原理计算，因为这时实际上只要计算有多少化学键被破坏[54]。这种方法对具有塑性的金属完全不适用。

用第一性原理来准确地计算材料的磁性或磁性材料的性能还有些困难。上面提到的局域密度近似结合动力学平均场(LDA+DMFT)方法[21-23]和局域密度近似结合Gutzwiller 近似的(LDA+Gutzwiller)变分法[24]比以前的方法[55-57]更可靠，但是计算量要大很多。

用第一性原理来计算半导体和绝缘体材料的热导率和电导率已有不少工作，例如文献[58-65]。金属材料(特别是任意成分的固溶体)的热导率和电导率的计算要困难一些，因为涉及其中的自由电子的运动[66]。

从分子动力学和蒙特卡洛方法(包括从头计算分子动力学[67-68])中可以获得的信息包括热力学性能、反应途径、结构、点缺陷和位错迁移率、晶界能和晶界移动性、析出相尺寸等[69-72]。这方面有很多小组在进行研究。

第一性原理计算可以直接用来设计功能材料，因为这时只需要计算某种或几种物理性能，而且大多数情况下不需要计算微观组织。很成功的例子有Ceder小组用第一性原理设计锂电池中的材料[73-75]。另一个例子是超硬材料的设计[76-79]。

3.2 CALPHAD方法

以上所提到的第一性原理计算的Gibbs自由能还达不到相图计算所需要的准确度。多元合金的成分和加工工艺的设计现在最常用和最可靠的方法是CALPHAD[80-83]。CALPHAD方法已经成为很多公司和研究机构材料设计的中坚。它不仅能计算多元合金在不同温度下的各个相的成分、体积分数、稳定温度范围、相变温度、热力学量(如Gibbs自由能、活度)等，还经常用来计算动力学模拟所需的相变驱动力、扩散过程的热力学参数(thermodynamic factor用来建立多元合金中的扩散系数矩阵)、凝固过程模拟所需的参数(潜热、元素偏析、比热、液相和固相温度等)。

CALPHAD中的各相的热力学参数是用实验结果(主要是二元相图和三元相图再加上形成焓、混合焓、比热、活度等)拟合/优化出来的，因此实验结果特别是三元相图是拟合可靠的热力学参数的重要输入。从第一性原理计算的热力学量虽然不能直接用来建立CALPHAD数据库，但可以用来作为拟合过程的参考值和上下限。这个上下限实际上对优化结果的可靠性很重要。

CALPHAD方法的框架已很成熟，现在的发展主要集中在建立可靠的数据库和扩展数据库中所包括的元素，未来的发展会从热力学、扩散迁移率、摩尔体积[84-86]等性能推广到其他性能以用于多种不同材料的设计。把CALPHAD计算与相场方法结合起来预测材料的微观结构和性能也是一些小组正在进行的工作。CALPHAD计算的应用例子多不胜举[81-83,87]。

3.3 显微组织预测

相场方法[88-93]是显微组织预测的主要方法。它最大的优点是不需要跟踪界面，从而不需要对显微组织的初始形貌进行提前设定，也不需要假定形貌不变，因此相场方法可以模拟复杂显微组织的演变。图2列出了两个例子[94-95]。另外一个重要的优点是相场方法可以把各种效应(弹性、磁场、温度场、电场、应力场等)都同时考虑进去，因此它经常用于机理性的研究。一个很好的例子是用相场方法预测和解释薄膜中的相和形貌的变化，从而建立其“相图”[96-97]。

相场方法的计算量比较大。常用的粗粒度的相场模型 (coarse-grained phase field model) 需要输入很多的信息，包括各相的Gibbs自由能、动力学参数(原子迁移率)、晶体结构、晶格常数、界面能和晶界能、各向异性的弹性模量、相界面的性能和缺陷，以及这些性能随温度和成分的变化。另外，还要对形核过程和界面厚度进行假设。CALPHAD方法能够提供各相的Gibbs自由能和原子迁移率随温度和成分变化的数据，其他数据现在需要从实验结果或第一性原理计算来获得。材料基因组工程的一项重要工作就是要建立各相的多种性能随成分和温度的变化关系，为材料设计和模拟提供数据和基础。

Kim-Kim-Suzuki (KKS)模型[98]，或叫多相相场模型[99-100]，把界面厚度与界面能完全分离开，从而使相场方法可以用来模拟任意尺度的材料体系，并且为多相体系和大规模的相场模拟奠定了基础。

微观相场模型(microscopic phase field model)只需要用第一性原理计算的广义层错能(GSF)和弹性模量来预测位错的核心结构和能量以及晶界的结构和能量，再用规则溶液模型和Cahn-Hilliard方法[101]就能预测平面型的异相界面的能量和结构以及临界核的形状和激活能[93]。

把位错也放到相场方法中进行模拟是一个很好的发展[102-106]，为以后从相场获得的显微组织中直接预测力学性能打下了基础。相场方法很早就已经用来模拟晶粒长大[107]，因此相场方法将来可能用来预测一些力学性能[93]。

把CALPHAD热力学数据库用到相场模拟中并不直截了当，通常需要对相场用的“有序参数”重新拟合一个函数。这种方法到多元系时困难特别突出。

在不考虑析出相的三维(空间)分布时，可采用TC-PRISMA[108-109]这样的程序来模拟析出相的形核和长大过程，这个程序直接调用Thermo-Calc和DICTRA的数据库，因此用起来时不需要像相场方法那么多的输入。但是要注意经典形核理论的局限性和所采用的界面能的大小。

3.4 力学性能预测和多尺度计算工具的集成

力学性能预测是一个非常复杂和困难的工作，因为它涉及位错的形成及其交互作用、位错与显微组织及其他缺陷之间交互作用、缺陷和裂纹的形成与长大、从原子尺度到微观尺度到介观尺度不同的机制作用、材料和缺陷与环境的交互作用等，而且力学性能包括很多性能：屈服强度、极限强度、延展性、耐疲强度、蠕变强度、断裂等。这方面的进展本文无法在此进行详细的描述。位错动力学方法[110-112]、晶体塑性理论[113-117]和微观力学方法[118-122]已被广泛采用。

有几种方法试图把从原子尺度到微观尺度到介观尺度到宏观尺度的模型和方法集成起来[123-129]，但还没有一种普适的、被广泛采用的方法和程序。材料基因组工程计划和ICME都希望这方面取得重大进展，结构材料的快速设计依赖着这方面的进步。

4 实验工具

材料领域已开发和使用了许多不同的实验工具用来研究材料的成分、晶体结构、缺陷、显微结构和各种性能[130]。由于篇幅的限制，本文不可能详细地介绍所有的实验工具，只能简要地介绍高通量的实验工具在建立材料成分-相-性能之间的关系以及对一些理论模型的验证方面的应用。

4.1 扩散多元节方法

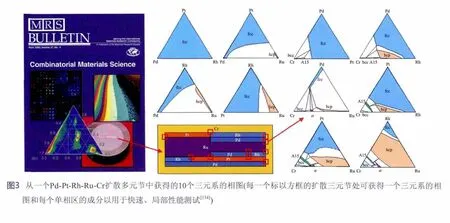
扩散多元节是一个把多个扩散偶和几个扩散三元节用热等静压方法结合在一起的样品[131-132]。在高温长时间退火后，元素之间会相互扩散并形成具有成分梯度的固溶体和中间相的扩散层。通过电子探针定量微区成分分析(EPMA)可获得穿越扩散区域的成分曲线，因为在两相界面处总是保持局部平衡，该处成分对应着两相平衡成分。这就是采用扩散偶测定相图的基础，已成功地用了几十年。扩散多元节中的三元节点区域(扩散三元节)可有效地测定三元相图的等温截面，这是金展鹏开创的方法[133]。这一方法可为建立多组元热力学数据库提供所需的大量的三元相图。 没有可靠的二元和三元相图的实验数据就不可能建立可靠的多组元热力学数据库。从一个Pd-Pt-Rh-Ru-Cr扩散多元节中获得的十个三元系的相图如图3所示[134]。要是用传统的平衡合金方法可能需要上百个不同成分的铸造合金才能测定这些相图，由此可见扩散多元节的高效率。 把从扩散多元节上测定的很多三元相图与平衡合金法测定的结果进行对比显示从扩散多元节上测定的相图很可靠，从而证实用扩散多元节来测定相图的普适性和可靠性[135]。

除了能够有效地测定相图以外，扩散多元节还可以用来有效地采集大量的二元系的扩散成分分布曲线，从而提取各个相的扩散系数随成分和温度的变化，以构建原子迁移率的数据库，用于材料析出长大及界面反应的模拟。作者的研究小组已开发了能从二元多相扩散成分分布曲线中快速提取出扩散系数的程序[136]。

4.2 高通量材料性能测试方法

扩散多元节的另外一个主要特征就是可以用来形成二元和三元体系中固溶体以及金属间化合物的完整的单相区的成分范围/梯度[131-132,134]。从这个意义上说，扩散多元节是一种有效的在单个试样上同时合成多种固溶体成分和化合物的方法。大约十几年前当本文作者开发扩散多元节的方法时，他有一个简单的想法：利用扩散偶和扩散多元节中形成的固溶体和化合物相的成分梯度来进行微区材料性能测试以快速获得成分-相-性能关系。从而不需要制备大批单个成分的合金试样就能建立成分-相-性能关系，这就大大地提高了性能测试的效率。要实现这一想法就必须开发一套新的具有微米级空间分辨率的材料性能测试工具。他和合作者们在过去几年中开发了一套新的基于飞秒激光表面反射的测量技术来准确扫描测试几个关键的物理性能，如热导率[137-138]、热膨胀系数[139]及比热容[140]。这些新的扫描性能测量工具与扩散多元节相结合能够数量级地提高材料性能测试的效率, 从而快速建立材料的成分-结构-性能关系以加速新材料开发和研究，为建立新的预测成分-相-结构－性能的理论体系提供大量的实验结果和理论验证。同时，这种系统、连续的测试可有效地发现异常效应，进一步采用聚焦离子束(FIB)提取微观样品进行分析，并结合理论计算快速建立新理论来解释异常效应，从而提高材料性能预测的精度和可靠性。

热导率的微区测试方法是基于双束飞秒激光的时域热反射技术(TDTR)[137-138]，其测量精度和空间分辨率可分别达到±8%和2～4 mm。该技术在一个小时内可以收集到100格点乘100个格点的热导率图，从而形成热导率像，就像扫描电镜(SEM)显示微观组织像一样。

金属和大多数金属间化合物主要由自由电子迁移来做热传导，因此，这些材料的热导率对元素替换、点缺陷的形成和有序转变特别敏感，从而可以用来研究这些现象。元素替换和点缺陷的形成都会增加电子散射，从而降低热导率；晶体结构的有序化则减少电子散射，从而提高热导率。一个Ni-Ni45.5Al54.5扩散偶的热导率像是一个很好的例子，如图4所示[141]。采用微区测试法从扩散偶中获得的热导率值与Terada等[142-143]采用20个铸造合金大块试样测量的值符合得很好。这一结果明确显示精确的热导率-成分关系可通过在扩散试样中的成分梯度上进行微区测量来获得，而不需要制备多个单成分的合金试样。图4也清楚地显示了固溶度对fcc相、有序—无序转变对Ni3Al相，以及点缺陷对b-NiAl相的热导率的影响[141]。

充分利用这一新的热导率测试技术，通过对多个扩散多元节中的很多个扩散偶进行测量，我们收集到了大量与成分相关的热导率数据，多于前人研究结果的总和。热导率图可以用来研究固溶体和金属间化合物中的点缺陷，也可以用来研究第三组元添加到二元金属间化合物中的元素替换方式(点阵优先取代)[141,144]。

把探测激光束移到离加热激光束几个微米的位置，再检测由加热激光束产生的微区表面热膨胀引起的探测激光束的偏转，进而用时域探测激光束偏转(TD-PBD)的方法可得到微区热膨胀系数(CTE)。该方法的精度可以达到±6 %[139,145]。从Fe-Ni和 Ni-Pt 两个扩散偶上获得的室温下CTE 随成分的变化如图5所示[139,145]。在没有制备任何单个合金样品情况下，这些数据清楚地揭示了成分Ni的原子数分数约为35%的扩散偶区域合金的因瓦(Invar)效应。微区测量的结果和Guillaume[146]利用很多个单成分铸造合金得到的结果符合得很好(Guillaume因为发现因瓦效应而获得1920年的诺贝尔物理学奖)。

图4 Ni-Ni45.5Al54.5 扩散偶及其热导率图[141]: (a) 扩散偶SEM图像；(b) 图(a)中虚线包围区域的热导率图；(c) 由扩散偶方法测量的与成分和相相关的热导率值与Terada等[142-143]采用单个合金大块试样的测量值的对比图；(d) 图(b)中热导率值的色标

图5 用时域探测激光束偏转(TD-PBD)微区CTE 测量方法从(a)Fe-Ni和(b) Ni-Pt 扩散偶上获得的CTE 随成分的变化[139,145-146]

Fe-Ni扩散偶形成的完整成分变化范围的样品可以用来系统地研究因瓦效应的机理[141]。低量的MeV氩离子(Ar+)照射后的测量发现Fe-Ni合金的CTE在因瓦区域(如Ni的原子数分数为30%～37%)随照射量的增加而升高；而其他成分的Fe-Ni合金的CTE 基本上没有变化。在因瓦成分为Fe65Ni35的合金中，在照射离子浓度达到1.2×1014ions/cm2时，CTE从照射前的0.5×10-6K-1增加到4.3×10-6K-1。这个结果表明原子间的短程有序在因瓦效应中起到了重要作用[147]。

在Ni-Pt扩散偶中用PD-PBD测量的CTE结果是另外一个很好的例子，它清楚地显示当完整的成分范围与微区性能测量相结合时，研究更有系统性[143]。从图5(b)中可以清楚地看到，成分Pt的原子数分数在32%～63%的范围内，CTE有小幅度的增加。假如用一些(比如10个)单个合金来测量CTE随成分的变化，这个小幅度增加的趋势可能在测量误差中丢失。需要强调的是，我们报道的热导率和热膨胀值并不仅仅是一种趋势，而是可以存档的实验值，和用单个大块样品测量的结果一样好。

热膨胀系数测量的两个例子(图5)可用来说明实验测量的另一个重要作用：系统地揭示异常效应。在Fe-35%Ni成分附近的因瓦效应通过测量一个Fe-Ni扩散偶的微区热膨胀系数就清楚地显示出来[139]；同样Ni-Pt扩散偶的热膨胀系数测量结果表明在Pt成分处于32%～63%范围时热膨胀系数有异常的增加[145]。利用在成分梯度上进行微区测量的系统性来从实验中发现这些异常行为是非常重要的，而与理论分析相结合可以帮助解释这些行为(有序、磁性转变、点缺陷……)，再用FIB提取扩散样品中的特定位置的微区/局部样品进行更详细的机理研究来验证理论的结果。这样一个集成研究能够更有效地建立预测的理论和模型，实验和理论研究的紧密结合将会导致实质性的快速的进展。

上面的例子显示了高效率测量相图、扩散系数、热导率和热膨胀系数的方法，其他的性能如弹性常数[148-149]、比热熔(CP)[140,150]和居里温度[144]随成分的变化关系也可以高效地测量出来。纳米压痕可以用来测量微尺度下的硬度和弹性模量[131-133,148-149,151]；光学椭圆偏振技术可以用来精确地测量微尺度下的光学性质[152-153]；消逝微波探针(EMP) 可以用来测量陶瓷材料的介电常数[154-155]；微尺度四点探针可以用来测量电导率[156-157]，不过当空间分辨率降低到几个微米时，这种方法还不够方便。关于这些先进的工具的详细综述可以在文献[144]中找到。

值得一提的是，最近也开发了一种叫频域热反射测量CP的方法[150]。它的精度还没有详细的报道，估计和时域热反射测量CP的精度相当[140]。这些工具可广泛地用于研究相变的热力学和测量建立热力学数据库所需的CP值。

Uchic及其合作者开发了一种用FIB制作微米尺度的柱子、薄片和拉伸试样的方法[158-159]，如图6所示。在这些微尺度样品上进行微尺度压缩、弯曲和拉伸可以得到材料强度和延展性的信息。只有达到临界直径时(取决于不同的材料和微观结构)，在圆柱压缩和拉伸试样上获得的微观测试结果才和大块材料的数据相符合；在低于临界直径时，位错受到限制并且数目有限，再加上一些随机现象和其他因素一起控制着变形过程，因此结果和大块样品有时相差很远。要得到有用的、可靠的强度、延展性和弹性数据，仍然需要做很多工作。

这些工具结合具有成分变化和不同相的样品，如扩散多元节或材料芯片[160]，能够高效地建立成分-相-结构－性能关系，从而加速材料信息学的发展和材料模型的检验以及新材料的设计。

4.3 数字化三维微观结构的表征与分析

近年来，数字化三维微观结构表征和数字化重建取得了长足的进展。早期的工作是用机械抛光获得一层一层的二维图像[161]，再把二维图像用数学方法在计算机上形成数字化的三维结构。最近的进展包括采用不同的方法来进行连续切片，其中包括FIB[162]和飞秒激光烧蚀[163]。每种方法都有其优缺点，这些方法和三维原子探针一起可用于不同尺度的三维微观结构的表征与分析。背散射电子衍射(EBSD)[164-165]是取向成像和评估晶粒尺寸的重要工具之一。三维成像现在不仅包括微观组织信息，也包含晶体结构和微区成分等三维信息，因此三维信息变成多模式信息。

材料性能(尤其是力学性能)的准确预测需要知道微观结构的细节，包括成分不均匀、组织分布和各向异性。 三维微观结构可以用来有效地验证微观组织的演化模型并揭示机制，比如三维微观结构的研究已开始对困扰了材料学界几十年的疲劳裂纹萌生的问题提出新的机制[166]。

数字化的微观结构是预测结构材料宏观性能必需的信息，特别是相的分布和界面性能以及每个相在微观结构下的性能。 以上所描述的高空间分辨率实验工具不仅能建立每个相/晶体结构的成分与性能的关系，整个微观结构下的微区性能的空间分布都是可定义的。在开发高空间分辨率实验工具以前，大多数材料的性能只能用大块样品测量，因此得到的结果是整个样品的平均值或最低值(取决于测试哪种性能)。除非使用新的微区材料性能测试工具, 并且除非样品是完全均匀的单相，某个特定相/晶体结构的某个特定成分的微区性能以前是无法获得的。能够考虑微区性能的空间分布的模型才会更正确地预测材料的宏观性能。

除了高通量性能测量及数字化三维微观结构表征以外，另一组实验也是非常可取的：模型验证试验。用精心设计的严格的实验来验证和改进模型非常有效，一个很好的例子就是用渗碳实验来研究扩散引起的长大过程中的相变机制[167-168]。这种直接、有效的模型验证试验应该推广。材料基因组计划中所需要的和所发展的模型和理论需要得到快速、高效的实验验证。

4.4 组合材料学方法

大多数的功能材料是以薄膜的形式使用，因此以薄膜为主的组合材料学(combinatorial materials science)方法，或叫材料芯片技术[160]，在功能材料的研究与开发中有非常重要的作用。这个领域已经有很好的综述[144,169-175]，所以在这里不再重复。

实验工具平台的建设还需要继续开发新的微区材料性能测试方法来高通量地测试各种其他的性能，并大量采用这些方法来快速建立材料性能数据库；也需要开发多尺度的材料性能测试方法和材料显微组织及缺陷的快速测量方法，以满足材料基因组计划中的材料计算和设计的需求。这些实验工具可提高材料研究与开发的系统性，特别是可以高效地揭示与研究异常效应，从而对于理论模型的改进提出要求和依据。这些高通量的材料性能测试技术将有可能像扫描电镜一样被广泛使用，从而导致材料性能测试和研究从宏观到微观、从离散到连续、从分散到系统的变革。这些新的性能测量工具与扩散多元节或材料芯片技术相结合，能数量级地提高材料性能测试的效率, 从而快速建立材料的成分-结构-性能关系以加速新材料开发和研究，为建立新的预测成分-相-结构-性能的理论体系提供大量的实验结果和理论验证。

5 数据库及材料信息学

材料信息学[176-179]还处于启蒙阶段，显著地落后于生物信息学。生物学、生物医学和基因组研究领域发表的文章及其摘要的内容都有强制性的具体规则以方便检索和使用，相关的数字数据资料均要求以所需格式存放在指定的数据库中。相对来说，材料领域对数据沉积、原始数据保存、摘要的内容和文章内容的要求过于宽松。

结构材料通常需要经过很多道工序才能制造成部件。材料的最终性能(特别是对结构敏感的性能)通常与加工/工艺过程的细节有关，也与微观组织结构的细节相关。要最有效地使用这些材料的性能数据，必须详细地记录材料的整个制造和加工过程、样品制备、测试方法和条件等，最好把每一步的三维微观结构也记载下来。这个记录过程本身就太繁琐并费时费力，需要开发自动化的记录和储存的方式和软件。

建立对结构不敏感的各种物理和化学性能的数据库要相对简单一些，特别是如果采用上面介绍的计算与实验相结合的高通量的方法。CALPHAD 数据库的建立和广泛使用为其他性能数据库的建立提供了非常宝贵的先例。

现在材料数据库很分散，比如，美国NIST、日本NIMS、英国NPL的数据库强调的内容不一样，数据格式、存储程序、完整程度、开放程度等也不同。没有一个国际标准就很难把这些分散的数据库有机地集成起来，美国NIST正在积极促成一个国际通用的材料数据库标准。

大规模的高通量计算将会提供大量而系统的数据，对这些数据进行快速的验证是高通量实验方法最可发挥作用的方式之一。把计算数据与实验数据有效地集成起来，既可以相互补充又可以相互验证。这个过程中必须清楚地保留元数据(metadata)和每组数据的起源信息，让使用者可以判断数据的可靠性。

材料界对材料数据库开放程度应该有一个现实的态度，总是会有保密的数据和收费的数据库，在整个数据库的宇宙里商业数据库有它存在必要性。要政府机构几十年后仍然对所有的数据库进行维护和升级是非常困难的，商业数据库如热力学数据库和Granta公司的材料数据库对材料数据的收集、整理、维护、更新和升级有很大的贡献。

有了材料数据库还必须开发材料信息学以充分利用数据库来加速材料设计，材料信息学将是材料基因组工程非常重要的研究方向之一。它必须充分利用现代的计算机科学和信息学的方法并以生物信息学和天体信息学为榜样来快速发展，以满足材料设计的需求。

6 成功的例子

美国国家研究理事会(NRC)最近发表的报告《轻质化技术在军用飞机、舰船和车辆中的应用》中引用了两个成功的ICME合金设计实例[180]。 一个是由 Olson 领导设计由QuesTek创新公司开发的Ferrium S53飞机着陆架用齿轮钢[181-182]；另一个是GE开发的燃气涡轮机用GTD262高温合金[180,183]。作者作为共同发明人(江亮博士是主导发明者)参与了GTD262合金的设计和开发。它的设计和开发从概念到生产只用了4年时间，研发所用经费是以前同类合金的开发成本的1/5左右。通过把计算热力学相稳定性的预测与GE内部的材料性能模型和数据库的整合，我们设计GTD262的成分一次到位，没有像以前开发合金那样要经过几次来来回回的重复实验才能达到成分的优化。因为设计时考虑到了很多因素，如可铸性、可焊性和抗氧化等，中试和生产过程中也没有出现任何问题。

GTD262合金的设计是一个很好的ICME的例子。但希望它的成功不要给人一种错觉，以为现在就可以在把一个全新的合金的研发时间缩短到4年之内。GTD262是修改一个现有的合金(GTD222)而获得的。在GTD222的成分附近，GE有过去的经验数据库以帮助我们设计。如果是一个成分远离现有合金的全新的合金，我们现在还没有所需的以物理/机制为基础的模型和性能数据库来进行合金设计。材料基因组工程就是要建立这样的模型和性能数据库来实现快速设计新材料。

7 结语

材料基因组工程/计划不仅仅是要开发快速、可靠的计算方法和相应的计算程序，而且也要开发高通量的实验方法来对理论进行快速验证并为数据库提供必需的输入，还要建立普适、可靠的数据库和材料信息学工具，以加速新材料的设计和使用。因为材料成分－结构－性能关系(特别是结构材料)的复杂性，要实现计算机快速材料设计，计算工具、实验工具和数据库都缺一不可。

有一些材料性能，如弹性模量，可以通过第一性原理得到有效且可靠的计算值[184-185]。在这种情况下，实验测量的目的就偏重于验证所采用的理论与模型的正确性，以及发现一些理论模型中可能没有考虑到的异常效应。对于其他的如热导率这样的性能，由于目前还没有开发出可靠有效的计算方法，因此我们就需要通过实验测量获取大量的数据，从而建立/验证数学模型。总之，为了建立数字化关系的框架和某些物理性能的数据库，实验与理论研究相互结合是至关重要的。

计算工具这些年虽然发展非常快，但是还远远不能满足新材料设计所需。需要研发出一批普适的材料设计和优化的程序，就像其他工程领域广泛使用的程序一样(有限元、流体力学、计算机辅助设计等)，这样才能把材料设计的周期缩短到与产品设计周期相当或更短，使得开发的最佳材料能及时地用到产品中来提高产品的性能。

现在已建立的理论和方法基本可以从成分预测微观组织结构(图7)，但从微观组织结构预测材料宏观性能的理论和方法还有待建立。对结构材料来说，特别需要：①建立相的各种性能随成分和温度变化的科学理论和数据库，②建立从缺陷的形成和分布来预测材料宏观性能的理论基础，③建立和有效集成多尺度模型。没有这些支柱就无法建立从微观组织结构预测材料宏观性能的桥梁(图7)。

图7 结构材料设计现状的形象说明。现在基本可以从成分预测微观组织结构，但还需要建立几个理论支柱才能建立从微观组织结构预测材料宏观性能的桥梁 (右边的图借自Granta 公司)

前面提到，第一性原理计算可以直接用来设计功能材料，因为这时只需要计算某种或几种物理性能，而且大多数情况下不需要计算微观组织，所以情况与图7中描述的结构材料大不一样。 很成功的例子有Ceder 小组用第一性原理设计锂电池中的材料[73-75]。

材料基因组计划正在大力推动国际公认的数据库结构和材料信息学工具的建立。这样，材料基因组工程的三个技术平台的科学基础正在快速发展并达到了“临界点”，是材料科学从“炒菜”到设计的大好时机。国家需要建立支持工业界采用计算材料设计新技术的机制，并大力提倡以应用为背景的材料研究与开发。在开发重要实用材料的过程中大力促进材料设计方法和工具的发展。另外，各高校和研究院所在培养新一代材料工程师方面也有重大的责任，计算工具在他们的课程中应变得越来越重要。材料基因组工程和ICME旨在材料领域建立一个新的以理论模型和预测优先、实验验证在后的“文化”，从而取代现有的以经验和实验为主的材料研发的理念。

(2013年10月25日收稿)

[1]Materials Genome Initiative for Global Competitiveness [EB/OL].2001. http://www.whitehouse.gov/sites/default/files/microsites/ostp/materials_genome_initiative-final.pdf.

[2]National Research Council. Integrated Computational Materials Engineering: A Transformational Discipline for Improved Competitiveness and National Security [M/OL]. Washington, DC:The National Academies Press, 2008. http://www.nap.edu/catalog.php?record_id=12199.

[3]“材料科学系统工程”香山科学会议第S14次学术讨论会[EB/OL].(2011-12-07). http: //159.226.97.16/ConfRead.aspx?ItemID=1998.

[4]COLLINS F S, MORGAN M, PATRINOS A. The human genome project: lessons from large-scale biology [J]. Science, 2003, 300: 286-290.

[5]FISCHER C, TIBBETTS K J, MORGAN D, et al. Predicting crystal structure by merging data mining with quantum mechanics [J]. Nature Mater, 2006, 5: 641-646.

[6]CEDER G, MORGAN D, FISCHER C, et al. Data-mining-driven quantum mechanics for the prediction of structure [J]. MRS Bull, 2006,31: 981-985.

[7]CURTAROLO S, MORGAN D, CEDER G. Accuracy of ab initio methods in predicting the crystal structures of metals: a review of 80 binary alloys [J]. Calphad, 2005, 29: 163-211.

[8]HART G L W, BLUM V, WALORSKI M J, et al. Evolutionary approach for determining first principles Hamiltonians [J]. Nature Mater, 2005, 4: 391-394.

[9]WANG Y, LV J, ZHU L, et al. Crystal structure prediction via particleswarm optimization [J]. Phys Rev B, 2010, 82: 094116-1-094116-8.

[10]WANG Y, LV J, ZHU L, et al. CALYPSO: A method for crystal structure prediction [J]. Comp Phys Commun, 2012, 183: 2063-2070.

[11]MAJZOUB E H, OZOLIŅŠ V. Prototype electrostatic ground state approach to predicting crystal structures of ionic compounds:application to hydrogen storage materials [J]. Phys Rev B, 2008, 77:104115-1-104115-13.

[12]WOLVERTON C, OZOLIŅŠ V, ASTA M. Hydrogen in aluminum:first-principles calculations of structure and thermodynamics [J]. Phys Rev B, 2004, 69: 144109-1-144109-16.

[13]WOLVERTON C, OZOLIŅŠ V. Hydrogen storage in calcium alanate:first-principles thermodynamics and crystal structures [J]. Phys Rev B,2007, 75: 064101-1-064101-15.

[14]CHEN X, ZHANG Y, WANG Y, et al. Structure determination of an amorphous compound AlB4H11[J]. Chem Sci, 2012, 3: 3183-3191.

[15]PETTIFOR D G. A chemical scale for crystal-structure maps [J]. Solid State Commun, 1984, 51: 31-34.

[16]VILLARS P, GIRGIS K. Regularities in binary intermetallic compounds [J]. Z Metallk, 1982, 73: 455-462.

[17]SEISER B, DRAUTZ R, PETTIFOR D G. TCP phase predictions in Ni-based superalloys: structure maps revisited [J]. Acta Mater, 2011,59: 749-763.

[18]KRESSE G, FURTHMÜLLER J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set [J]. Comput Mater Sci,1996, 6: 15-50.

[19]KRESSE G, FURTHMULLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Phys Rev B, 1996, 54: 11169-11186.

[20]PERDEW J P, ZUNGER A. Self-interaction correction to densityfunctional approximations for many-electron systems [J]. Phys Rev B,1981, 23: 5048-5079.

[21]LICHTENSTEIN A I, KATSNELSON M I, KOTLIAR G. Finitetemperature magnetism of transition metals: an ab initio dynamical mean-field theory [J]. Phys Rev Lett, 2001, 87: 067205-1-067205-4.

[22]KOTLIAR G, SAVRASOV S Y, HAULE K, et al. Electronic structure calculations with dynamical mean-field theory [J]. Rev Modern Phys,2006, 78: 865-951.

[23]ANISIMOV V I, KONDAKOV D E, KOZHEVNIKOV A V, et al.Full orbital calculation scheme for materials with strongly correlated electrons [J]. Phys Rev B, 2005, 71: 125119-1-125119-16.

[24]DENG X, WANG L, DAI X, et al. Local density approximation combined with Gutzwiller method for correlated electron systems:Formalism and applications [J]. Phys Rev B, 2009, 79: 075114-1-075114-20.

[25]ZUNGER A, WEI S-H, FERREIRA L G, et al. Special quasi-random structures [J]. Phys Rev Lett, 1990, 65: 353-356.

[26]SOVEN P. Coherent-potential model of substitutional disordered alloys[J]. Phys Rev, 1967, 156: 809-813.

[27]FAULKNER J S. The modern theory of alloys [J]. Prog Mater Sci,1982, 27: 1-187.

[28]VELICKÝ B, KIRKPATRICK S, EHRENREICH H. Single-site approximations in the electronic theory of simple binary alloys [J].Phys Rev, 1968, 175: 747-766.

[29]BELLAICHE L, VANDERBILT D. Virtual crystal approximation revisited: application to dielectric and piezoelectric properties of perovskites [J]. Phys Rev B, 2000, 61: 7877-7882.

[30]KIKUCHI R. Superposition approximation and natural iteration calculation in cluster-variation method [J]. J Chem Phys, 1974, 60:1071-1080.

[31]SANCHEZ J M, DUCASTELLE F, GRATIAS D. Generalized cluster expansion of multicomponent systems [J]. Physica A, 1984, 128: 334-350.

[32]DE FONTAINE D, WOLVERTON C. Cluster approach to firstprinciples thermodynamics of crystals [J]. Prog Theor Phys, 1994, 115:115-130.

[33]CEDER G. A derivation of the Ising model for the computation of phase diagrams [J]. Comput Mater Sci, 1993, 1: 144-150.

[34]ZUNGER A. Statics and dynamics of alloy phase transformation [M].NATO ASI Series. Vol 319. New York: Plenum Press, 1994: 361.

[35]VAN DE WALLE A. Multicomponent multisublattice alloys,nonconfigurational entropy and other additions to the alloy theoretic automated toolkit [J]. Calphad, 2009, 33: 266-278.

[36]VAN DE WALLE A, ASTA M. Self-driven lattice-model Monte Carlo simulations of alloy thermodynamic properties and phase diagrams [J].Model Simul Mater Sci Eng, 2002, 10: 521-538.

[37]VAN DE WALLE A, ASTA M, CEDER G. The alloy theoretic automated toolkit: a user guide [J]. Calphad, 2002, 26: 539-553.

[38]VAN DE WALLE A, CEDER G. Automating first-principles phase diagram calculations [J]. J Phase Equil, 2002, 23: 348-359.

[39]VAN DE WALLE A. A complete representation of structure-property relationships in crystals [J]. Nature Mater, 2008, 7: 455-458.

[40]PARLINSKI K, LI Z Q, KAWAZOE Y. First-principles determination of the soft mode in cubic ZKD2 [J]. Phys Rev Lett, 1997, 78: 4063-4066.

[41]BARONI S, GIANOZZI P, TESTA A. Green's-function approach to linear response in solids [J]. Phys Rev Lett, 1987, 58: 1861-1864.

[42]KRESSE G, FURTHMÜLLER J, HAFNER J. Ab initio force constant approach to phonon dispersion relations of diamond and graphite [J].Europhys Lett, 1995, 32: 729-734.

[43]GIANNOZZI P, DE GIRONCOLI S, PAVONE P, et al. Ab initio calculation of phonon dispersions in semiconductors [J]. Phys Rev B,1991, 43: 7231-7242.

[44]YU R, SINGH D, KRAKAUER H. All-electron and pseudopotential force calculations using the linearized-augmented-plane-wave method[J]. Phys Rev B, 43, 1991: 6411-6422.

[45]MANTINA M, WANG Y, ARROYAVE R, et al. First-principles calculation of self-diffusion coefficients [J]. Phys Rev Lett, 2008, 100:215901-1-215901-4.

[46]MANTINA M, WANG Y, CHEN L-Q, et al. First principles impurity diffusion coefficients [J]. Acta Mater, 2009, 57: 4102-4108.

[47]HUANG S, WORTHINGTON D L, ASTA M, et al. Calculation of impurity diffusivities in α-Fe using first-principles methods [J]. Acta Mater, 2010, 58: 1982-1993.

[48]VAN DER VEN A, CEDER G. First principles calculation of the interdiffusion coefficient in binary alloys [J]. Phys Rev Lett, 2005, 94:045901-1-045901-4.

[49]SWOBODA B, VAN DER VEN A, MORGAN D. Assessing concentration dependence of fcc metal alloy diffusion coefficients using kinetic Monte Carlo [J]. J Phase Equili Diff, 2010, 31: 250-259.

[50]VAN DER VEN A, YU H C, CEDER G, et al. Vacancy mediated substitutional diffusion in binary crystalline solids [J]. Prog Mater Sci,2010, 55: 61-105.

[51]VAN DER VEN A, CEDER G, ASTA M, et al. First-principles theory of ionic diffusion with nondilute carriers [J]. Phys Rev B, 2001, 64:184307-1-184307-7.

[52]MORUZZI V L, JANAK J F, SCHWARZ K. Calculated thermal properties of metals [J]. Phys Rev B, 1988, 37: 790-799.

[53]MOUNET N, MARZARI N. First-principles determination of the structural, vibrational and thermodynamic properties of diamond,graphite, and derivatives [J]. Phys Rev B, 2005, 71: 205214-1-205214-14.

[54]SIMUNEK A, VACKAR J. Hardness of covalent and ionic crystals:first-principle calculations [J]. Phys Rev Lett, 2006, 96: 085501-1-085501-4.

[55]ANISIMOV V I, ARYASETIAWAN F, LICHTENSTEIN A I. Firstprinciples calculations of the electronic structure and spectra of strongly correlated systems: the LDA + U method [J]. J Phys Cond Matter, 1997, 9: 767-808.

[56]SANDRATSKII L M. Noncollinear magnetism in itinerant-electron systems: theory and applications [J]. Adv Phys, 1998, 47: 91-160.

[57]ROSENGAARD N M, JOHANSSON B. Finite-temperature study of itinerant ferromagnetism in Fe, Co, and Ni [J]. Phys Rev B, 1997, 55:14975-14986.

[58]VAN DE WALLE C G, NEUGEBAUER J. First-principles calculations for defects and impurities: applications to III-nitrides [J]. J Appl Phys,2004, 95: 3851-3879.

[59]SKOUG E J, CAIN J D, MORELLI T D, et al. Lattice thermal conductivity of the Cu3SbSe4-Cu3SbS4solid solution [J]. J Appl Phys,2011, 110: 023501-1-023501-5.

[60]YANG J, MEISNER G P, CHEN L. Strain field fluctuation effects on lattice thermal conductivity of ZrNiSn-based thermoelectric compounds [J]. Appl Phys Lett, 2004, 85: 1140-1142.

[61]ZHANG Y, SKOUG E, CAIN J, et al. First-principles description of anomalously low lattice thermal conductivity in thermoelectric Cu-Sb-Se ternary semiconductors [J]. Phys Rev B, 2012, 85: 054306-1-054306-6.

[62]BROIDO D A, MALORNY M, BIRNER G, et al. Intrinsic lattice thermal conductivity of semiconductors from first principles [J]. Appl Phys Lett, 2007, 91: 231922-1-231922-3.

[63]STACKHOUSE S, STIXRUDE L, KARKI B B. Thermal conductivity of periclase (MgO) from first principles [J]. Phys Rev Lett, 2010, 104:208501-1-208501-4.

[64]ADLER D, FEINLEIB J. Electrical and optical properties of narrowband materials [J]. Phys Rev B, 1970, 2: 3112-3134.

[65]HUANG B L, KAVIANY M. Ab initio and molecular dynamics predictions for electron and phonon transport in bismuth telluride [J].Phys Rev B, 2008, 77: 125209-1-125209-19.

[66]EBERT H, VERNES A, BANHART J. Anisotropic electrical resistivity of ferromagnetic Co-Pd and Co-Pt alloys [J]. Phys Rev B, 1996, 54:8479-8486.

[67]CAR R, PARRINELLO M. Unified approach for molecular dynamics and density-functional theory [J]. Phys Rev Lett, 1985, 55: 2471-2474.[68]CAR R, PARRINELLO M. Structural, dynamical, and electronic properties of amorphous silicon: an ab initio molecular-dynamics study[J]. Phys Rev Lett, 1988, 60: 204-207.

[69]BERENDSEN H J C, POSTMA J P M, VAN GUNSTEREN W F, et al. Molecular dynamics with coupling to an external bath [J]. J Chem Phys, 1984, 81: 3684-3690.

[70]KRESSE G, HAFNER J. Ab initio molecular dynamics for liquid metals [J]. Phys Rev B, 1993, 47: 558-561.

[71]SOLER J M, ARTACHO E, GALE J D, et al. The Siesta method for ab initio order-N materials simulation [J]. J Phys Cond Matter, 2002, 14:2745-2779.

[72]ANDERSEN H C. Molecular dynamics at constant pressure and/or temperature [J]. J Chem Phys, 1980, 72: 2384-2393.

[73]KANG B, CEDER G. Battery materials for ultrafast charging and discharging [J]. Nature, 2009, 458: 190-193.

[74]KANG K, MENG Y S, BRÉGER J, et al. Electrodes with high power and high capacity for rechargeable ltihium batteries [J]. Science, 2006,311: 977-980.

[75]CEDER G, CHIANG Y M, SADOWAY D R, et al. Identification of cathode materials for lithium batteries guided by first-principles calculations [J]. Nature, 1998, 392: 694-696.

[76]MATAR S F, BETRANHANDY E, NAKHL M, et al. Structural geomimetism: a conceptual framework for devising new materials from first principles [J]. Prog Solid State Chem, 2006, 34: 21-66.

[77]VEPŘEK S. The search for novel, superhard materials [J]. J Vac Sci Technol A, 1999, 17: 2401-2420.

[78]HAINES J, LÉGER J M, BOCQUILLON G. Synthesis and design of superhard materials [J]. Ann Rev Mater Sci, 2001, 31: 1-23.

[79]KANER R B, GILMAN J J, TOLBERT S H. Designing superhard materials [J]. Science, 2005, 308: 1268-1269.

[80]KAUFMAN L, BERNSTEIN H. Computer calculation of phase diagrams with special reference to refractory metals [M]. Waltham:Academic Press, 1970.

[81]SAUNDERS N, MIODOWNIK A P. CALPHAD (calculation of phase diagrams): a comprehensive guide [M]. Oxford: Pergamon/Elsevier,1998.

[82]LUKAS L H, FRIES S G, SUNDMAN B. Computational thermodynamics: the CALPHAD method [M]. Cambridge: Cambridge University Press, 2007.

[83]KATTNER U R. Phase diagrams for lead-free solder alloys [J]. JOM,1997, 49: 14-19.

[84]LU X-G, SELLEBY M, SUNDMAN B. Implementation of a new model for pressure dependence of condensed phases in Thermo-Calc[J]. Calphad, 2005, 29: 49-55.

[85]LU X-G, SELLEBY M, SUNDMAN B. Accessments of molar volume and thermal expansion for selected bcc, fcc and hcp metallic elements[J]. Calphad, 2005, 29: 68-89.

[86]HALLSTEDT B, DUPIN N, HILLERT M, et al. Thermodynamic models for crystalline phases. Composition dependent models for volume, bulk modulus and thermal expansion [J]. Calphad, 2007, 31:28-37.

[87]HACK K. The SGTE casebook: thermodynamics at work [M]. 2nd ed.Cambridge: Woodhead Publishing, 2008.

[88]WHEELER A A, BOETTINGER W J, MCFADDEN G B. Phase-field model for isothermal phase transitions in binary alloys [J]. Phys Rev A,1992, 45: 7424-7439.

[89]WARREN J A, BOETTINGER W J. Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-field method [J]. Acta Metall Mater, 1995, 43: 689-703.

[90]WANG Y, KHACHATURYAN A G. Three-dimensional field model and computer modeling of martensitic transformations [J]. Acta Mater,1997, 45: 759-773.

[91]CHEN L-Q. Phase-field models for microstructure evolution [J]. Annu Rev Mater Sci, 2002, 32: 113-140.

[92]BOETTINGER W J, WARREN J A, BECKERMANN C, et al. Phasefield simulation of solidification [J]. Annu Rev Mater Sci, 2002, 32:163-194.

[93]WANG Y, LI J. Phase field modeling of defects and deformation [J].Acta Mater, 2010, 58: 1212-1235.

[94]ZHOU N, SHEN C, MILLS M J, et al. Large-scale three-dimensional phase field simulation of γ’-rafting and creep deformation [J]. Phil Mag, 2010, 90: 405-436.

[95]JIN Y M, ARTEMEV A, KHACHATURYAN A G. Three dimensional phase field model of low-symmetry martensitic transformation in polycrystal: simulation of z2 martensite in AuCd alloys [J]. Acta Mater, 2001, 49: 2309-2320.

[96]HAENI J H, IRVIN P, CHANG W, et al. Room-temperature ferroelectricity in strained SrTiO3[J]. Nature, 2004, 430: 758-761.

[97]LU Y, WANG C P, GAO Y P, et al. Microstructure map for selforganized phase separation during film deposition [J]. Phys Rev Lett,2012, 109: 086101-1-086101-5.

[98]KIM S G, KIM W T, SUZUKI T. Phase-field model for binary alloys[J]. Phys Rev E, 1999, 60: 7186-7197.

[99]EIKEN J, BOTTGER B, STEINBACH I. Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application [J]. Phys Rev E, 2006, 73: 066122-1-066122-9.

[100]TIADEN J, NESTLER B, DIEPERS H J, et al. The multiphase-f i eld model with an integrated concept for modeling solute diffusion [J].Phys D, 1998, 115: 73-86.

[101]CAHN J W, HILLIARD J E. Free energy of a non-uniform system III:Nucleation in a two-component incompressible fluid [J]. J Chem Phys,1959, 31: 688-699.

[102]WANG Y U, JIN Y M, CUITIÑO A, et al. Nanoscale phase field microelasticity theory of dislocations: model and 3D simulations [J].Acta Mater, 2001, 49: 1847-1857.

[103]WANG Y U, JIN Y M, CUITIÑO A M, et al. Phase field microelasticity theory and modeling of multiple dislocation dynamics [J]. Appl Phys Lett, 2001, 78: 2324-2326.

[104]RODNEY D, LE BOUAR Y, FINEL A. Phase field methods and dislocations [J]. Acta Mater, 2003, 51: 17-30.

[105]SHEN C, WANG Y. Phase field model of dislocation networks [J].Acta Mater, 2003, 51: 2595-2610.

[106]ZHOU N, SHEN C, MILLS M J, et al. Modeling displacive-diffusional coupled dislocation shearing of gamma prime precipitates in Ni-base superalloys [J]. Acta Mater, 2011, 59: 3484-3497.

[107]FAN D, CHEN L-Q. Computer simulation of grain growth using a continuum field model [J]. Acta Mater, 1997, 45: 611-622.

[108]CHEN Q, JEPPSSON J, ÅGREN J. Analytical treatment of diffusion during precipitate growth in multicomponent systems [J]. Acta Mater,2008, 56: 1890-1896.

[109]CHEN Q, JOU H-J, STERNER G. TC-PRISMA users' guide and examples [M/OL]. Thermo-Calc Software AB, Stockholm, Sweden,2011. [2012-09-04]. http://www.thermocalc.se/Library.htm.

[110]ZBIB H M, RHEE M, HIRTH J P. On plastic deformation and the dynamics of 3D dislocations [J]. Inter J Mech Sci, 1998, 40: 113-127.

[111]MIGUEL M C, VESPIGNANI A, ZAPPERI S, et al. Intermittent dislocation flow in viscoplastic deformation [J]. Nature, 2001, 410:667-671.

[112]HORSTEMEYER M F, BASKES M I, PLIMPTON S J. Length scale and time scale effects on the plastic flow of fcc metals [J]. Acta Mater,2001, 49: 4363-4374.

[113]ASARO R J. Crystal plasticity [J]. J Appl Mech, 1983, 50: 921-934.

[114]LEBENSOHN R A, TOMÉ C N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: application to zirconium alloys [J]. Acta Metall Mater,1993, 41: 2611-2624.

[115]FLECK N A, MULLER G M, ASHBY M F, et al. Strain gradient plasticity-theory and experiment [J]. Acta Metall Mater, 1994, 42: 475-487.

[116]HUTCHINSON J W. Plasticity at the micron scale [J]. Inter J Solids Struct, 2000, 37: 225-238.

[117]GURTIN M E. A gradient theory of single-crystal viscoplasticity that accounts for geometrically necessary dislocations [J]. J Mech Phys Solids, 2002, 50: 5-32.

[118]ASARO R J. Micromechanics of crystals and polycrystals [J]. Adv Appl Mech, 1983, 23: 1-115.

[119]BUDIANSKY B. Micromechanics [J]. Comput Struct, 1983, 16: 3-12.[120]GAO H, RICE J R. A first-order perturbation analysis of crack trapping by arrays of obstacles [J]. J Appl Mech, 1989, 56: 828-836.

[121]RUGGIERI C, PANONTIN T L, DODDS JR R H. Numerical modeling of ductile crack growth in 3-D using computational cell elements [J]. Inter J Fract, 1996, 82: 67-95.

[122]WILKINSON D S, POMPE W, OESCHNER M. Modeling the mechanical behaviour of heterogeneous multi-phase materials [J]. Prog Mater Sci, 2001, 46: 379-405.

[123]WEINAN E, HUANG Z. Matching conditions in atomistic-continuum modeling of materials [J]. Phys Rev Lett, 2001, 87: 135501-1-135501-13.

[124]SHILKROT L E, MILLER R E, CURTIN W A. Multiscale plasticity modeling: coupled atomistic and discrete dislocation mechanics [J]. J Mech Phys Solids, 2004, 52: 755-787.

[125]ROTERS F, EISENLOHR P, HANTCHERLI L, et al. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: theory, experiments,applications [J]. Acta Mater, 2010, 58: 1152-1211.

[126]VAITHYANATHAN V, WOLVERTON C, CHEN L-Q. Multiscale modeling of precipitate microstructure evolution [J]. Phys Rev Lett,2002, 88: 125503-1-125503-4.

[127]HOYT J J, ASTA M, KARMA A. Atomistic and continuum modeling of dendrite solidification [J]. Mater Sci Eng R, 2003, 41: 121-163.

[128]LI J, NGAN A H W, GUMBSCH P. Atomistic modeling of mechanical behavior [J]. Acta Mater, 2003, 51: 5711-5742.

[129]BULATOV V, ABRAHAM F F, KUBIN L, et al. Connecting atomistic and mesoscale simulations of crystal plasticity [J]. Nature, 1998, 391:669-672.

[130]ROBERTSON I M, SCHUH C A, VETRANO J S, et al. Towards an integrated materials characterization toolbox [J]. J Mater Res, 2011,26: 1341-1383.

[131]ZHAO J-C. A Combinatorial approach for structural materials [J]. Adv Eng Mater, 2001, 3: 143-147.

[132]ZHAO J-C. The diffusion-multiple approach to designing alloys [J].Annu Rev Mater Sci, 2005, 35: 51-73.

[133]JIN Z. A study on the range of stability of sigma phase in some ternary system [J]. Scand J Metall, 1981, 10: 178-187.

[134]ZHAO J-C, JACKSON M R, PELUSO L A, et al. Overview: a diffusion-multiple approach for mapping phase diagrams, hardness,and elastic modulus [J]. JOM, 2002, 54(7): 42-45.

[135]ZHAO J-C. Reliability of the diffusion-multiple approach for phase diagram mapping [J]. J Mater Sci, 2004, 12: 3913-3925.

[136]ZHANG Q, ZHAO J-C. Extracting interdiffusion coefficients from binary diffusion couples using traditional methods and a forwardsimulation method [J]. Intermetallics, 2013, 34: 132-141.

[137]HUXTABLE S, CAHILL D G, FAUCONNIER V, et al. Thermal conductivity imaging at micrometre-scale resolution for combinatorial studies of materials [J]. Nature Mater, 2004, 3: 298-301.

[138]ZHENG X, CAHILL D G, ZHAO J-C. Thermal conductivity imaging of thermal barrier coatings [J]. Adv Eng Mater, 2005, 7: 622-626.

[139]ZHENG X, CAHILL D G, WEAVER R, et al. Micron-scale measurements of the coefficient of thermal expansion by timedomain probe beam deflection [J]. J Appl Phys, 2008, 104: 073509-1-073509-9.

[140]WEI C, ZHENG X, CAHILL D G, et al, Micron resolution spatiallyresolved measurement of heat capacity using dual-frequency timedomain thermoreflectance [J]. Rev Sci Instr, 2013, 84: 071301-1-071301-9.

[141]ZHAO J-C, ZHENG X, CAHILL D G. Thermal conductivity mapping of the Ni–Al system and the beta-NiAl phase in the Ni–Al–Cr system[J]. Scripta Mater, 2012, 66: 935-938.

[142]TERADA Y, OHKUBO K, MOHRI T, et al. Thermal conductivity in nickel solid solutions [J]. J Appl Phys, 1997, 81: 2263-2268.

[143]TERADA Y, OHKUBO K, MOHRI T, et al. A comparative study of thermal conductivity in alloys and compounds [J]. Mater Sci Eng A,2000, 278: 292-294.

[144]ZHAO J-C. Combinatorial approaches as effective tools in the study of phase diagrams and composition-structure-property relationships [J].Prog Mater Sci, 2006, 51: 557-631.

[145]CAHILL D G, ZHENG X, ZHAO J-C. Spatially resolved measurements of thermal stresses by picosecond time-domain probe beam deflection [J]. J Thermal Stresses, 2010, 33: 9-14.

[146]GUILLAUME C E. Discovery of the anomaly of the nickel steels [J].Proc Phys Soc London, 1920, 32: 374-404.

[147]ZHENG X, CAHILL D G, ZHAO J-C. Effect of MeV ion irradiation on the coefficient of thermal expansion of Fe–Ni Invar alloys: a combinatorial study [J]. Acta Mater, 2010, 58: 1236-1241.

[148]OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments [J]. J Mater Res, 1992, 7: 1564-1580.

[149]DOERNER M F, NIX W D. A method for interpreting the data from depth-sensing indentation instruments [J]. J Mater Res, 1986, 1: 601-609.

[150]SCHMIDT A J, CHEAITO R, CHIESA M. A frequency-domain thermoreflectance method for the characterization of thermal properties[J]. Rev Sci Instr, 2009, 80: 094901-1-094901-6.

[151]LEE T Y, OHMORI K, SHIN C S, et al. Elastic constants of singlecrystal TiNx(001) (0.67≤x≤1.0) determined as a function ofxby picosecond ultrasonic measurements [J]. Phys Rev B, 2005, 71:144106-1-144106-6.

[152]TAKEUCHI I, YANG W, CHANG K-S, et al. Monolithic multichannel ultraviolet detector arrays and continuous phase evolution in MgxZn1-xO composition spreads [J]. J Appl Phys, 2003, 94: 7336-7340.

[153]FUKUMURA T, OHTANI M, KAWASAKI M, et al. Rapid construction of a phase diagram of doped Mott insulators with a composition-spread approach [J]. Appl Phys Lett, 2000, 77: 3426-3428.

[154]WEI T, XIANG X-D, WALLACE-FREEDMAN W G, et al. Scanning tip microwave near-field microscope [J]. Appl Phys Lett, 1996, 68:3506-3508.

[155]GAO C, WEI T, DUEWER F, et al. High spatial resolution quantitative microwave impedance microscopy by a scanning tip microwave nearfield microscope [J]. Appl Phys Lett, 1997, 71: 1872-1874.

[156]BOGGILD P, GREY F, HASSENKAM T, et al. Direct measurement of the microscale conductivity of conjugated polymer monolayers [J].Adv Mater, 2000, 12: 947-949.

[157]CHUNG S-Y, CHIANG Y-M. Microscale measurements of the electrical conductivity of doped LiFePO4[J]. Electroch Solid-State Lett, 2003, 6: A278-A281.

[158]UCHIC M D, DIMIDUK D M, FLORANDO J N, et al. Samples dimensions influence strength and crystal plasticity [J]. Science, 2004,305: 986-989.

[159]UCHIC M D, DIMIDUK D M. A methodology to investigate size scale effects in crystalline plasticity using uniaxial compression testing [J].Mater Sci Eng A, 2005, 400-401: 268-278.

[160]XIANG X-D, SUN X, BRICEÑO G, et al. A combinatorial approach to materials discovery [J]. Science, 1995, 268: 1738-1740.

[161]DEHOFF R T. Quantitative serial sectioning analysis: preview [J]. J Microsc, 1983, 131: 259-263.

[162]UCHIC M D, GROEBER M A, DIMIDUK D M, et al. 3D microstructural characterization of nickel superalloys via serialsectioning using a dual beam FIB-SEM [J]. Scripta Mater, 2006, 55:23-28.

[163]ECHLIN M P, MOTTURA A, TORBET C J, et al. A new TriBeam system for three-dimensional multimodal materials analysis [J]. Rev Sci Instr, 2012, 83: 023701-1-023701-6.

[164]DINGLEY D J, RANDLE V. Microtexture determination by electron backscatter diffraction [J]. J Mater Sci, 1992, 27: 4545-4566.

[165]SCHWARTZ A J, KUMAR M, ADAMS B L. Electron Backscatter Diffraction in Materials Science [M]. New York: Kluwer Academic/Plenum Press, 2000.

[166]MIAO J, POLLOCK T M, JONES J W. Microstructural extremes and the transition from fatigue crack initiation to small crack growth in a polycrystalline nickel-base superalloy [J]. Acta Mater, 2012, 60: 2840-2854.

[167]ZUROB H S, HUTCHINSON C R, BRECHET Y, et al. Kinetic transitions during non-partitioned ferrite growth in Fe–C–X alloys [J].Acta Mater, 2009, 57: 2781-2792.

[168]HUTCHINSON C R, FUCHSMANN A, ZUROB H S, et al. A novel experimental approach to identifying kinetic transitions in solid state phase transformations [J]. Scripta Mater, 2004, 50: 285-289.

[169]JANDELEIT B, SCHAEFER D J, POWERS T S, et al. Combinatorial materials science and catalysis [J]. Angew Chem Inter Ed, 1999, 38:2494-2532.

[170]FUKUMURA T, YAMADA Y, TOYOSAKI H, et al. Exploration of oxide-based diluted magnetic semiconductors toward transparent spintronics [J]. Appl Surf Sci, 2004, 223: 62-67.

[171]KOINUMA H, TAKEUCHI I. Combinatorial solid state chemistry of inorganic materials [J]. Nature Mater, 2004, 3: 429-438.

[172]MAIER W F, STOWE K, SIEG S. Combinatorial and high-throughput materials science [J]. Angew Chem Inter Ed, 2007, 46: 6016-6067.

[173]XIANG X-D. Combinatorial materials synthesis and screening: an integrated materials chip approach to discovery and optimization of functional materials [J]. Annu Rev Mater Sci, 1999, 29: 149-171.

[174]POTYRAILO R A, MIRSKY V M. Combinatorial and high-throughput development of sensing materials: the first ten years [J]. Chem Rev,2008, 108: 770-813.

[175]AMIS E J, XIANG X-D, ZHAO J-C. Combinatorial materials science:what's new since Edison? [J]. MRS Bull, 2002, 27: 295-300.

[176]RAJAN K. Materials informatics [J]. Mater Today, 2005, 8(10): 38-45.[177]SUKUMAR N, KREIN M, LUO Q, et al. MQSPR modeling in materials informatics: a way to shorten design cycles? [J]. J Mater Sci,2012, 47: 7703-7715.

[178]ARNOLD S M. Paradigm shift in data content and informatics infrastructure required for generalized constitutive modeling of materials behavior [J]. MRS Bull, 2006, 31: 1013-1021.

[179]LE PAGE Y. Data mining in and around crystal structure databases [J].MRS Bull, 2006, 31: 991-994.

[180]National Research Council. Application of lightweighting technology in military aircraft, vessels and vehicles [M]. Washington, D.C.: The National Academies Press, 2012: 118～119.

[181]KUEHMANN C J, OLSON G B. Computational materials design and engineering [J]. Mater Sci Technol, 2009, 25: 472-478.

[182]OLSON G B. Computational design of hierarchically structured materials [J]. Science, 1997, 277: 1237-1242.

[183]JIANG L, ZHAO J-C, FENG G. Nickel-containing alloys, method of manufacture thereof and articles derived therefrom [P]. World Patent Application WO2005056852, filed on September 29, 2004, published on June 23, 2005; U.S. Patent Application 20100135847, filed on October 21, 2009, published on June 3, 2010.

[184]LIU Z K. First-principles calculations and CALPHAD modeling of thermodynamics [J]. J Phase Equili Diff, 2009, 30: 517-534.

[185]LIU Z K. A materials research paradigm driven by computation [J].JOM, 2009, 61(10): 18-20.

A perspective on the Materials Genome Initiative

ZHAO Ji-cheng
Professor, Department of Materials Science and Engineering, The Ohio State University, Columbus, Ohio 43210, USA

U.S. President Obama introduced the Materials Genome Initiative (MGI) and clearly stated that the goal of MGI is “to discover, develop, manufacture, and deploy advanced materials at twice the speed than is possible today.” The pertinent whitepaper“Materials Genome Initiative for Global Competitiveness” released by the White House Office of Science and Technology Policy in June 2011 outlines the Materials Innovation Infrastructure as consisting of three platforms: computational tools, experimental tools and digital data. The MGI will accelerate materials design and deployment by: ①developing effective and reliable computational methods and software tools, ②developing high-throughput experimental methodologies to validate theories and to provide reliable experimental data to the materials databases, and ③establishing reliable and widely applicable databases and materials informatics tools. The ultimate intent of MGI is to usher in a new paradigm/culture of materials research and innovation where materials design is conducted by up-front simulations/predictions followed by key validation experiments in contrast to the current practice that is heavily based on experimental iterations and experiences.

Materials Genome Initiative, materials design, integrated computational materials engineering (ICME)

10.3969/j.issn.0253-9608.2014.02.002

(编辑：沈美芳)