引入强跟踪滤波器的IMM算法在导航定位解算中的应用

刘宇玺,吴 鹏,刘文祥,王飞雪

(国防科学技术大学电子科学与工程学院卫星导航定位技术工程研究中心,湖南 长沙 410073)

0 引 言

目前,全球四大卫星导航系统逐步发展完善,已有的北斗系统(BDS)、GPS和GLONASS三个全球导航系统已经能够提供导航定位服务[1]。但是,随着导航终端产品应用范围越来越广,应用场景日趋复杂多样化,即便是比较成熟的GPS导航系统也会出现定位效果较差的时候。例如,对于导航终端大范围应用的城市机动载体,经常工作在多动态环境下,而且对导航定位系统的精度和可靠性要求也较高,运用单一运动模型已经不能有效的估计载体的运动状态。近年来,学者们开始尝试利用多个模型进行估计,最早出现的是变维滤波算法,用低阶模型估计非机动状态,用高阶模型估计机动状态,模型之间属于硬切换,这种方法往往带有机动检测与切换的滞后性[2]。交互式多模型[4](IMM)则是一种基于软切换的目标跟踪方法。交互式多模型方法根据载体不同的运动状态应用不同的运动模型,各个模型滤波器之间通过估计状态组合实现交互,而模型之间基于一个马尔科夫链进行切换。最后不同模型滤波器相互融合得到最终估计结果。

本文利用“CV”模型和“当前”模型作为载体状态估计的基础模型。两种模型分别可以有效应对载体低动态运动和高动态运动,考虑到EKF滤波自身鲁棒性较差,容易受到参数设置的影响,本文将强跟踪滤波器引入交互式多模型算法中。针对EKF的缺陷,文献[5]中提出的基于强跟踪滤波器(STF)的“当前”统计模型自适应算法具有更好的机动跟踪性能。强跟踪滤波器由于渐消因子的引入,与标准扩展卡尔曼滤波器(EKF)相比有较强的鲁棒性,极强的跟踪能力,适中的计算复杂性。由于渐消因子的作用,强跟踪滤波器保持了不同时刻滤波残差序列处处正交。当存在模型不确定性时,通过在线调整增益可以使得残差保持高斯白噪声的性质。

本文主要论述了交互式多模型的基本原理,将强跟踪滤波器引入交互式多模型并应用于导航定位解算中,可以应对城市机动载体复杂多变的运动状态。仿真结果证明：相比于单模型估计和标准的IMM算法,本文提出的引入强跟踪滤波器的交互式多模型算法能够提高定位精度。

1 引入强跟踪滤波器的交互式多模型原理

交互式多模型算法主要包括五个步骤:

1)输入交互

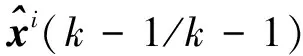
uk-1/k-1(j/i),

(1)

1)T)]uj/i(k-1/k-1)，

(2)

其中:

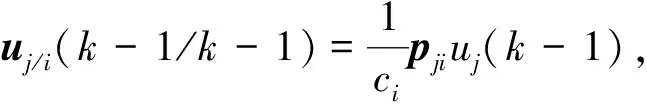
(3)

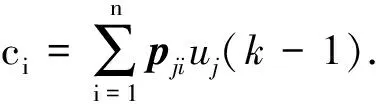
(4)

2)模型估计

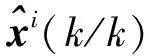
两个滤波器的似然函数为

Λi(k)=P[Z(k)/Mi(k),Zk-1].

(5)

由初始混合条件和协方差可以得到

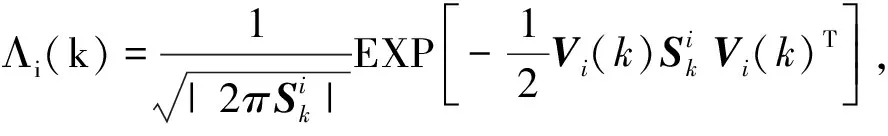
(6)

其中:

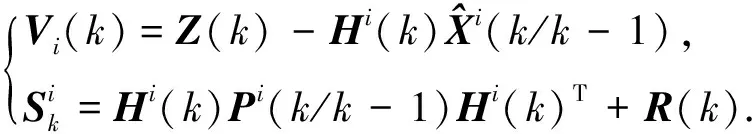
(7)

3)模型概率更新

(8)

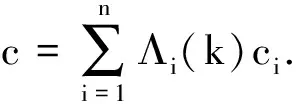
(9)

4)融合输出

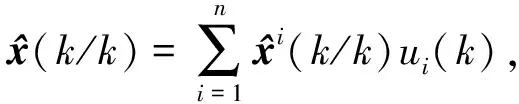
(10)

(11)

以上就是标准IMM算法的基本原理,标准IMM算法通常采用的都是扩展卡尔曼滤波器。这里类似于单个滤波器的卡尔曼滤波过程,不同的是需要计算两个模型。考虑到EKF跟踪强机动目标时鲁棒性较差的缺陷,本文在标准IMM算法的基础上引入强跟踪滤波器。

强跟踪滤波器具体过程为

(12)

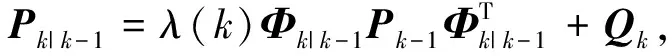
(13)

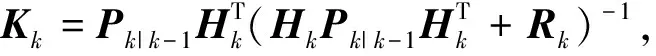
(14)

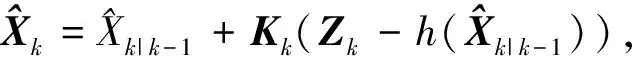
(15)

Pk=[Ι-KkHk]Pk|k-1.

(16)

由上式可以看出,相比于EKF滤波器,强跟踪滤波器在扩展卡尔曼滤波器的估计误差协方差阵中引入次优渐消矩阵,对不同数据通道进行渐消,使不同时刻的残差序列处处正交,使得滤波器能够较好的保持对强机动目标实际状态的跟踪。渐消因子的具体计算过程为

(17)

N(k)=Z0(k)-βR(k)-

H(k)Q(k-1)HT(k),

(18)

M(k)=H(k)φ(k-1)P(k)φT(k-1)HT(k),

(19)

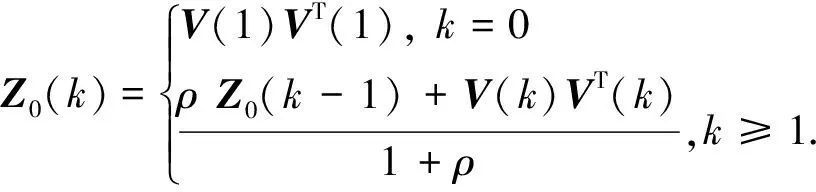
(20)

其中:ρ为遗忘因子,通常取值在[0,1]之间，本文中取值为0.9;β为弱化因子,根据经验取值,在本文中取值为1;而V(1)为初始残差值。从上述公式可以看出,当载体运动于一般机动时,预测值和估计值相差不大,此时渐消因子较小,强跟踪滤波器就退化为标准EKF滤波器;当运动状态发生突变时,滤波残差增大导致渐消因子增大,滤波增益得到自适应调节,迫使残差近似正交,从而提高状态变化时的跟踪性能。

2 滤波模型

本文所使用的IMM算法包含两个基础运动模型,“CV”模型和“当前”模型。

对于载体静止和低动态时,通常采用恒定速度模型,即“CV”模型,“CV”模型一般都进行匀速直线运动,因此可将运动载体的转弯、大气湍流而引起的加速度看作是匀速直线运动中的摄动,在运动模型中,将这种摄动作为随机噪声输入。以一维直线运动为例,CV模型的离散时间系统状态方程为

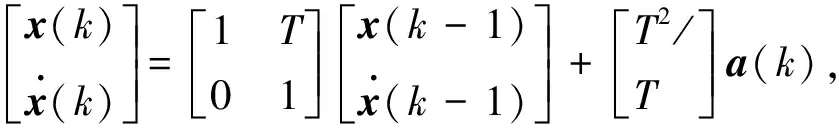
(21)

对于载体高动态时,通常采用“当前”模型匹配。由于在实际情况中载体的运动并不完全属于等速或等加速范围内,对此,Zhou和Kumar提出了一种“当前”统计模型[6],这种模型认为当目标以某一加速度机动时,下一时刻的加速度值是有限的,并且只能在当前加速度的某一邻域范围内。运动载体的加速度可表示为

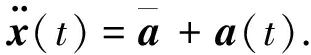
(21)

故系统状态方程可以表示为

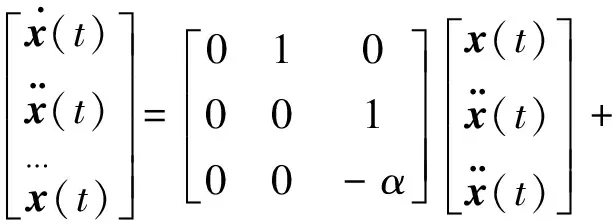
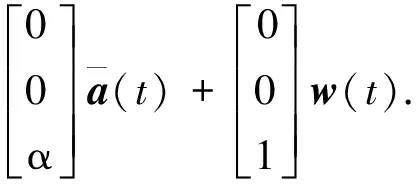
(22)

3 实验与分析

图1和图2是X轴和Y轴位置误差图,图3和图4是载体在机动阶段的局部仿真结果图。0～40 s,载体处于匀速运动状态;40～50 s,载体以加速度ax=-6 m/s2,ay=-4 m/s2做转弯运动;50～145 s,载体做匀速运动;145～160 s,载体再次做转弯运动,ax=4.5 m/s2,ay=3.7 m/s2;之后50 s内载体做匀速运动;在210～230 s和265～285 s载体再次进行两次加速转弯运动;之后载体一直保持匀速运动。由图示定位结果可以看出,本文提出的引入强跟踪滤波器的交互式多模型算法相比于CV模型在载体机动阶段定位误差较小,同时克服了“当前”模型在载体处于匀速运动等低动态下跟踪精度下降的缺点,强跟踪滤波器的引入使得载体对机动变化有了更好的鲁棒性。表1示出了利用不同方法得到的定位结果的位置误差方差值,在本组试验数据中,改进的交互式多模型算法相比于“当前”模型滤波和标准交互式多模型算法,分别可以将径向误差方差从19.11和16.78降低到13.24.

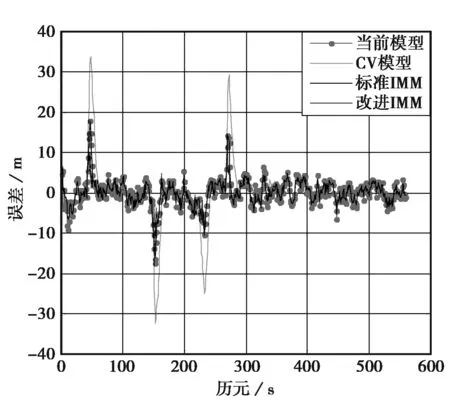
图1 X轴误差

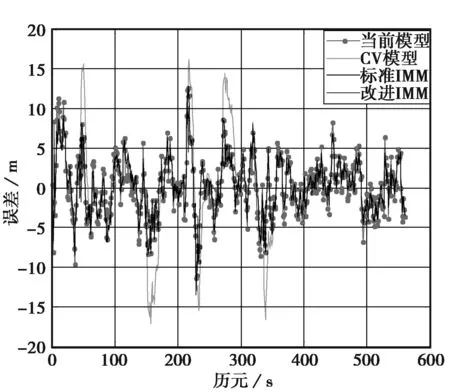
图2 Y轴误差

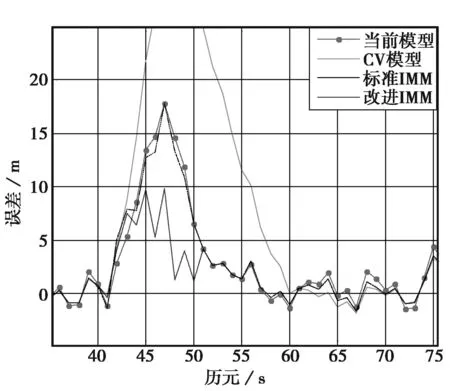
图3 机动局部放大图1

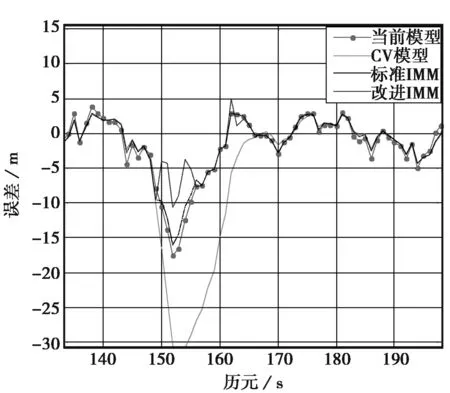
图4 机动局部放大图2

表1方差统计表

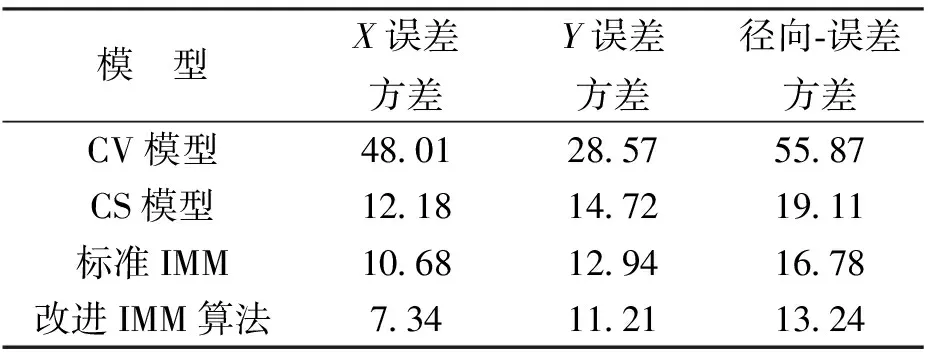
模 型X误差方差Y误差方差径向-误差方差 CV模型48.0128.5755.87 CS模型12.1814.7219.11 标准IMM10.6812.9416.78 改进IMM算法7.3411.2113.24

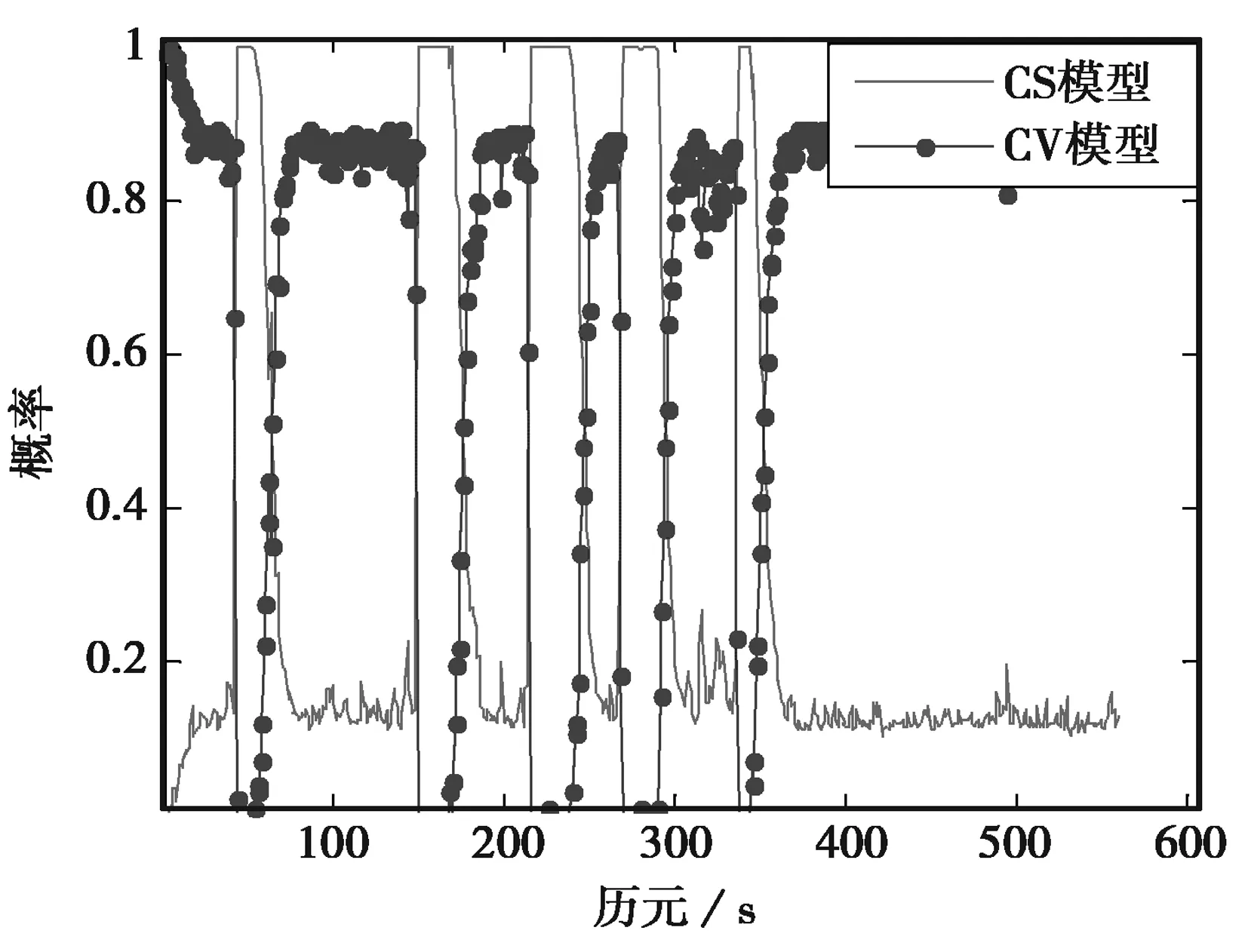
图5 模型概率图

图5示出了改进算法在处理过程中两种基础模型概率的变化曲线,从图中可以看出,根据算法原理,随着运动过程中载体机动状态的不断变化,不同模型匹配概率也随之自适应变化;图6示出了仿真实验中载体运动轨迹图,为了更加贴近载体实际运动状态,全过程融合了匀速、加速和转弯运动三种运动状态。

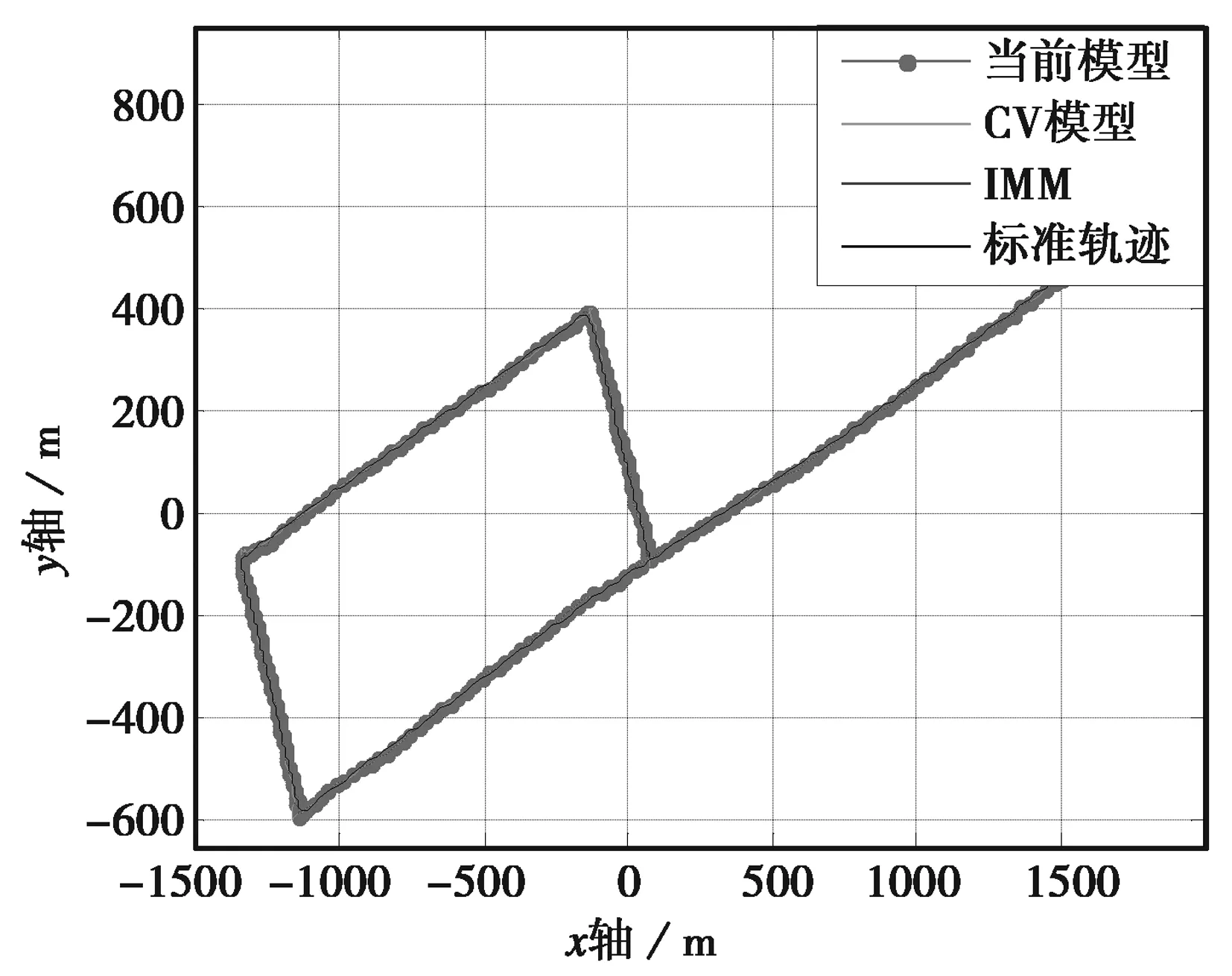
图6 载体运动轨迹图2

4 结束语

本文将机动目标跟踪领域应用广泛的交互式多模型算法引入到导航定位中,并结合Kalman滤波阐述了改进的IMM算法流程。利用信号源仿真机动载体运动轨迹对引进强跟踪滤波器的交互式多模型的定位性能进行分析,通过实验结果可以得到以下结论:

1)相比于单模型滤波,改进的交互式多模型可以在不增加较多复杂度情况下应对不同的动态场景,有效综合了两种基础模型的优点。

2)强跟踪滤波器的引入可以使得滤波器在载体处于高动态和动态转换阶段有着更好的鲁棒性。

3)交互式多模型算法中模型转移概率的获取是决定滤波精度的关键因素,如何更好的自适应载体运动状态实时更新模型转移概率是下一步研究的重点。

[1]KAPLAN E D. GPS原理与应用 [M]. 2 版. 寇艳红译,北京:电子工业出版社,2006.

[2]NDJENG A,GRUYER D,GLASER S.A Improvement of the proprioceptive-sensors based EKF and IMM localization[C]//The International IEEE Conference on Intelligent Transportation Systems,2008:900-905.

[3]刘贵喜,高恩克,范春宇.改进的交互式多模型粒子滤波跟踪算法[J].电子信息学报,2007,29(12):1009-5896.

[4]LI Rongx, JILKOV V P. Survey of maneuvering target tracking part v: Multiple-model methods[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1254-1280.

[5]范小军,刘 峰,秦 勇,等.基于STF的“当前”统计模型及自适应跟踪算法[J].电子学报,2006,34(6):981-984.

[6]JWO Dahjing, TSENG Chienhao.GPS navigation processing using the IMM-based EKF.[C]//3rdInternational Conference on Sensing Technology,2008.

[7]罗笑冰,王宏强,黎 湘.模型转移概率自适应的交互式多模型跟踪算法[J].电子信息学报，2005,10(10):1593-1595.

[8]ZHOU Hongren, KUMAR K S P. A current statistical model and adaptive algorithm for estimating maneuvering targets. AIAA.[J].Journal of Guidance, Control and Dynamics, 1984, 7(5):596-602.

[9]刘建书,李人厚,刘云龙.基于“当前”统计模型的交互式多模型算法[J].系统工程与电子技术,2008，30(7):1001-506.

[10]徐 敏,金以慧,杨瑞娟.基于强跟踪滤波器的多目标跟踪方法[J].传感器技术,2002,21(3):1000-9787.