高阶BOC调制信号无模糊跟踪技术性能比较

刘中伟,黄仰博,唐小妹,欧 钢

(国防科学技术大学电子科学与工程学院卫星导航定位技术工程研究中心,湖南 长沙 410073)

0 引 言

全球导航卫星系统最初采用的信号调制方式是BPSK-R(Binary Phase Shift Keying,二进制相移键控),为了满足应用精度和可靠性的需求,提升服务性能,现代化的导航信号和新增加的导航信号设计了新的调制方式[1]。其中,二进制偏移载波(BOC)调制广泛应用于GPS、Galileo、北斗等卫星导航定位系统。GPS现代化的军用信号采用BOCs(10,5)调制;Galileo E1 PRS信号采用BOCc(15,2.5)调制,E6 PRS信号采用BOCc(10,5)调制;北斗B1频点计划发射BOC(14,2)调制信号。与BPSK调制方式相比,BOC调制具有诸多优势:更好的信号跟踪性能、抗多径性能、良好的频谱分离特性,充分利用卫星导航分配的频率资源等[2]。BOC调制信号可以视为BPSK-R信号和方波副载波的乘积,它的一个重要特征是自相关函数的主峰较窄并有多个副峰,这给信号的接收带来了挑战。特别是对于高阶BOC调制信号,自相关函数副峰和主峰的幅值相差较小,在较强的噪声环境、严重的多径或干扰条件下,副峰的幅值甚至会超过主峰。副峰的存在可能造成错误锁定和模糊跟踪,给用户接收机带来不可接受的较大误差。为解决BOC调制信号自相关函数多峰特性对信号接收造成的错误锁定和模糊跟踪问题,目前提出的主要技术有:Bump-Jump算法[3],BPSK-like算法[4],

SCPC算法[5],双环路算法[6]。

本文首先说明BOC调制及其特征,指出高阶BOC信号跟踪面临的失锁和模糊问题,然后对常见的几种无模糊跟踪算法在高阶BOC信号跟踪时的有效性进行了分析,最后从硬件复杂度、计算复杂度、跟踪精度和跟踪稳定性多个方面对跟踪算法进行了比较,为接收机的设计提供了参考。

1 BOC调制及其特征

BOC调制信号可以视为BPSK-R信号和方波副载波的乘积,其原理图如图1所示。BOC调制表示为BOC(fs,fc),也简记为BOC(m,n),其中fs=m×1.023 MHz是方波副载波频率,fc=n×1.023 MHz是扩频码速率。BOC调制的阶数定义为一个扩频符号内的方波半周期数,即k=2fs/fc=2m/n,k一般选为偶数,并将k值较大的BOC调制称为高阶BOC调制,如BOC(14,2)。BOC调制根据方波副载波相位的不同分为BOCs(m,n)和BOCc(m,n),调制后的基带信号表示为

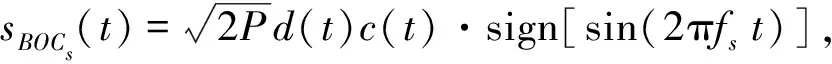
(1)

式中:P为发射信号功率;d(t)为导航数据码;c(t)为PRN扩频码;fs是方波副载波频率; sign为符号函数。

方波副载波的归一化能量谱密度表达式为:

(2i+1)fs),

(3)

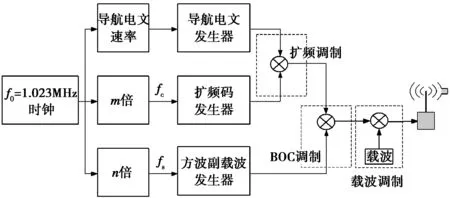
图1 BOC调制原理示意图

式中,i为整数,根据上式,Sg(f)可看作由一系列冲激信号组成,相邻冲激信号之间在频率上间隔2fs。功率在零频处为零,最大值在±fs处,各约占信号总功率的40.528%。因此,将主瓣以零频为中心的BPSK-R调制信号的频谱分裂到(2i+1)fs频率处即可得到BOC调制信号的频谱,i为整数。分裂的频谱有利于实现不同调制信号同时占用相同的载波中心频率并相互兼容。BOCs(10,5)、BOCs(14,2)信号功率谱密度如图2和图3所示:

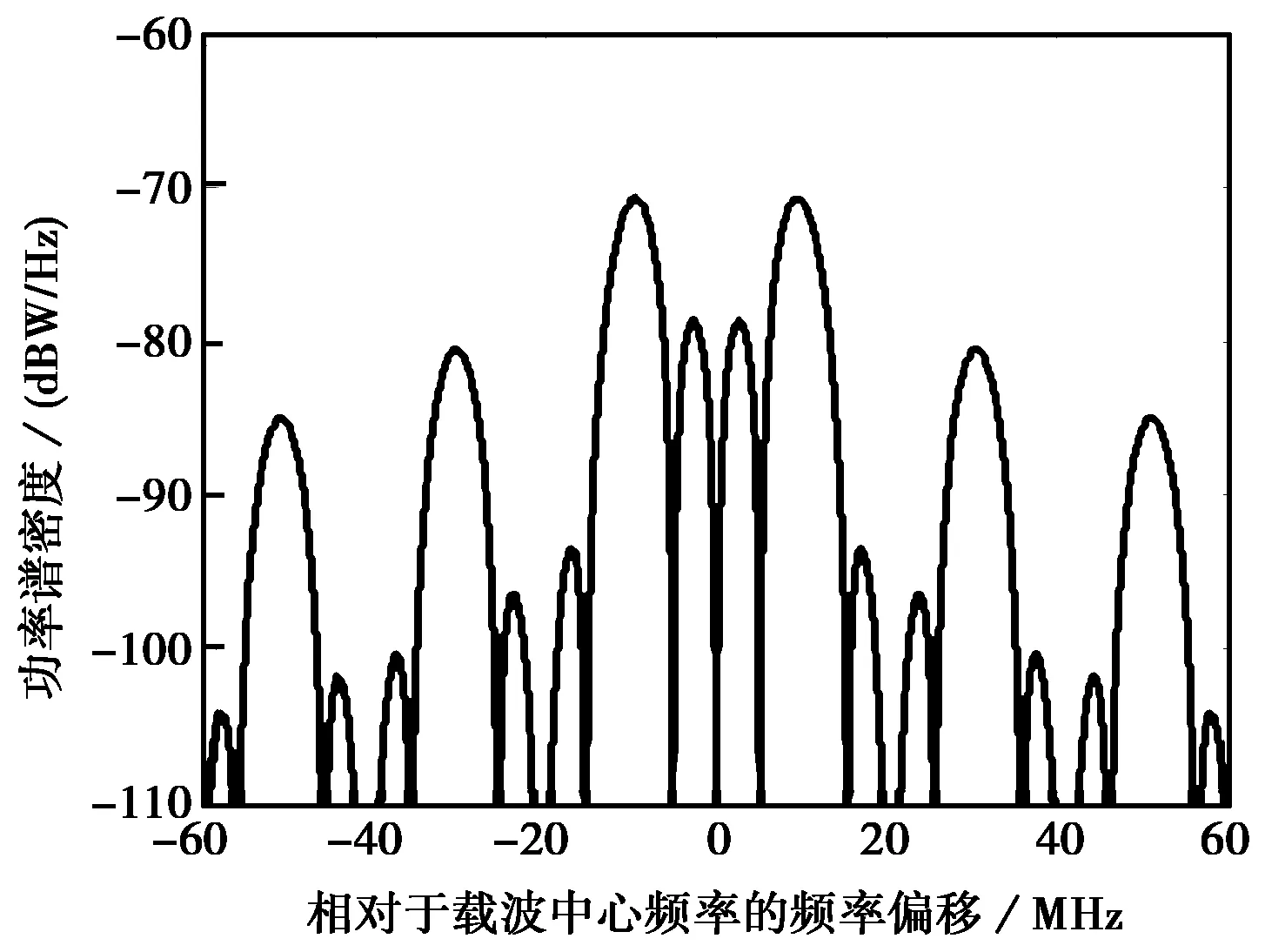
图2 BOCs(10,5)信号功率谱密度

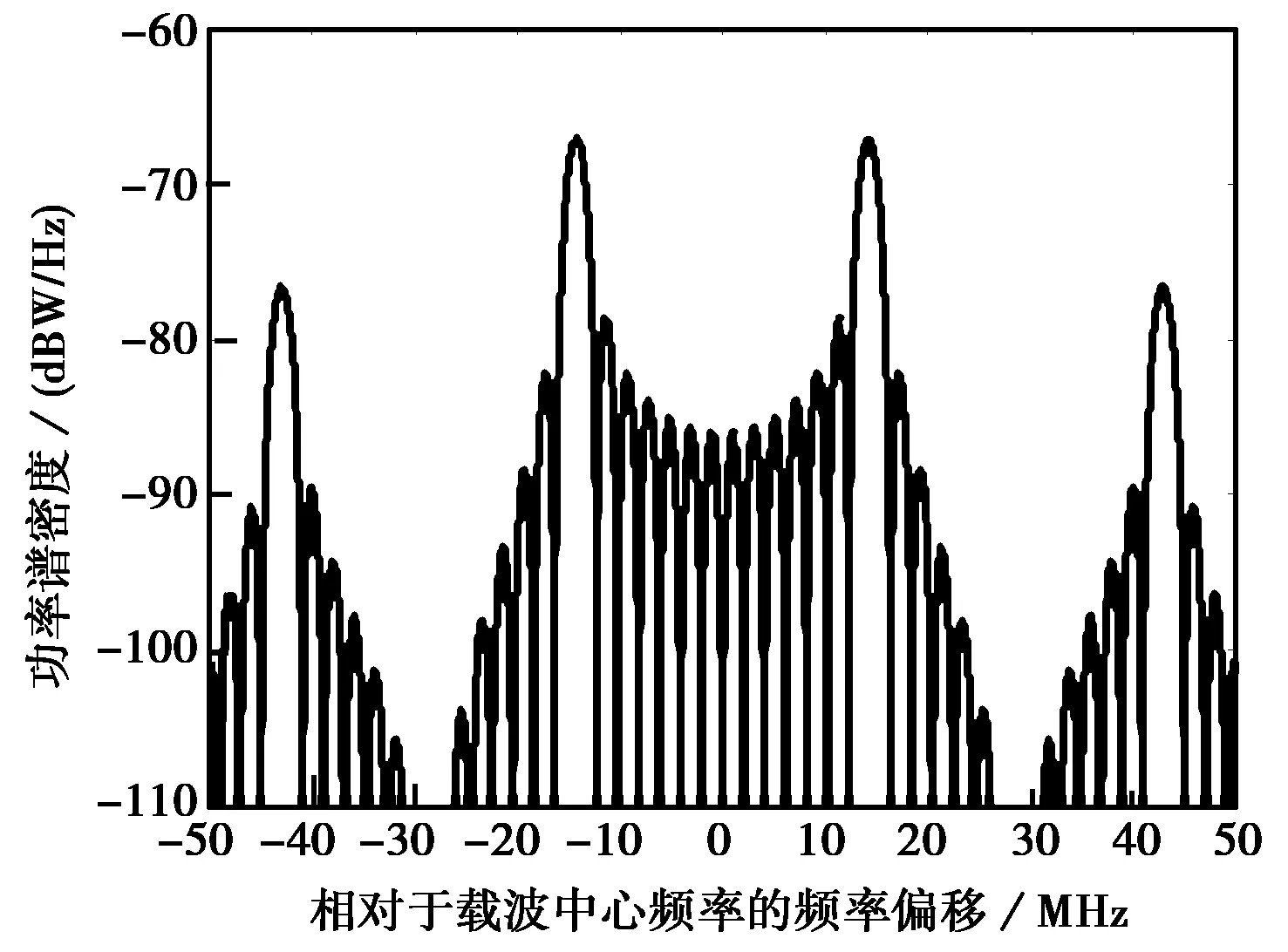
图3 BOCs(14,2)信号功率谱密度

可见,BOC调制阶数越高或副载波频率fs越大,则主瓣相对于载波中心频率偏移越远,各种调制信号功率谱特性如表1所示。

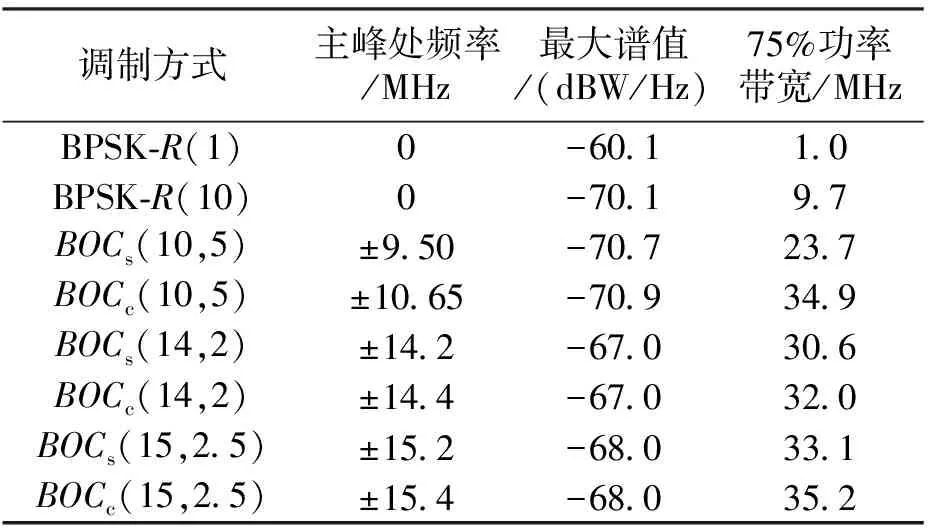
表1 几种调制信号功率谱特性参数

BPSK-R调制信号的自相关函数形状是三角形,主峰宽度为两个码片,但BOC调制信号的自相关函数却具有多峰特性。BOCs(10,5)和BOCs(14,2)的自相关函数如图4和图5所示,βr表示接收机预相关带宽。

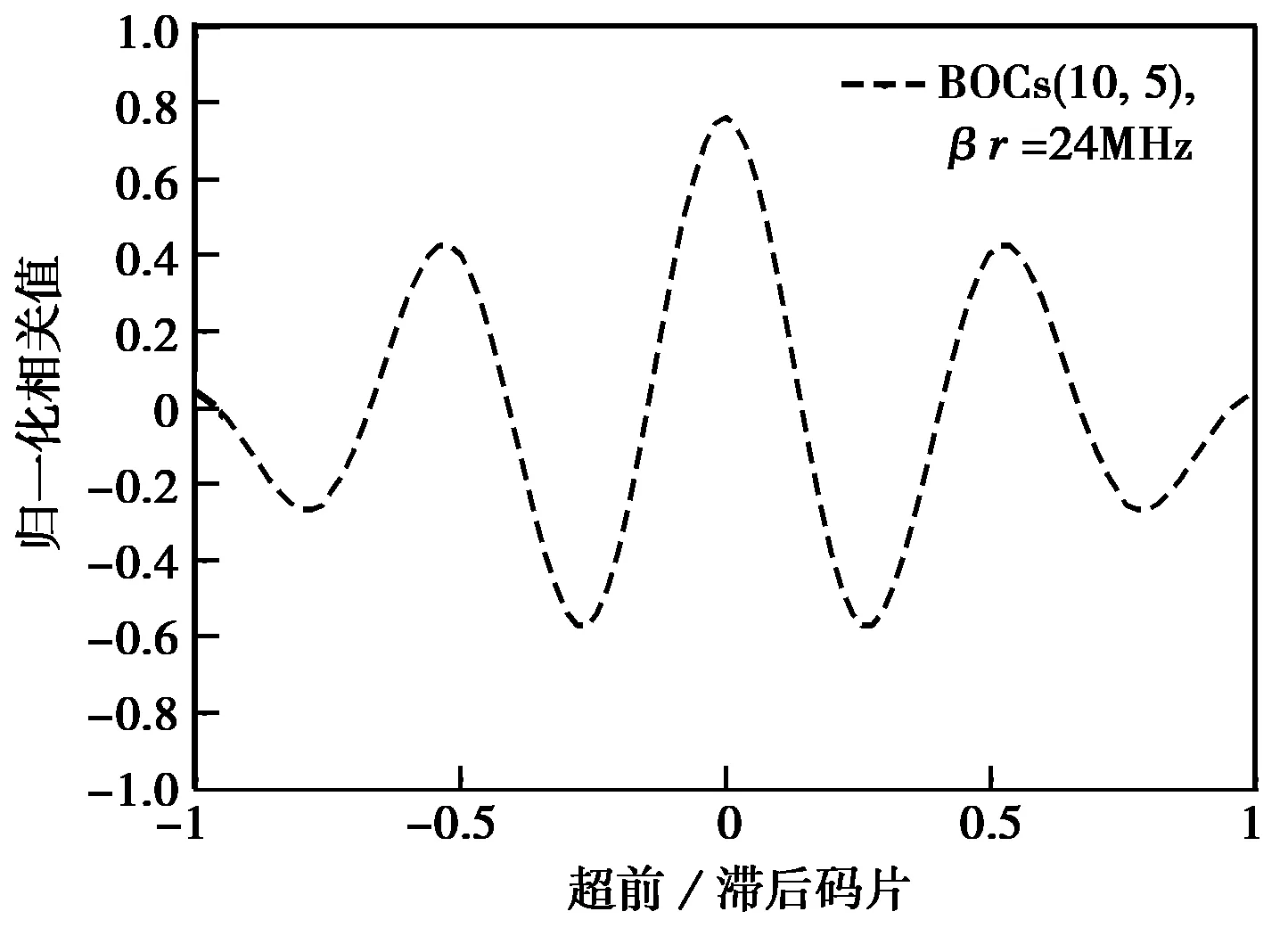
图4 BOCs(10,5)信号自相关函数

图5 BOCs(14,2)信号自相关函数

BOC调制信号的自相关函数正负峰的个数为2k-1,相邻峰之间的间隔为1/k码片,k为BOC调制的阶数。可见,BOC调制阶数越高,则相关函数副峰个数越多,相邻峰之间间隔越小,次峰与主峰幅值越接近。

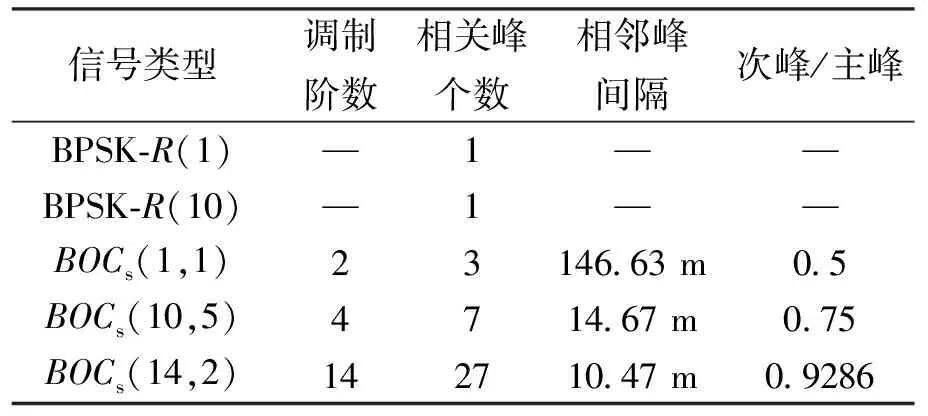
表2 几种调制信号自相关函数的参数

自相关函数的多峰特性给信号的接收带来了挑战,对于BOC(10,5)信号,采用非相干超前减滞后功率(EMLP)鉴别器得到的S曲线如图2所示,图中标记出6个错误锁定点,如果环路锁定在错误锁定点,会造成较大的测距误差。对于高阶BOC信号,采用传统跟踪算法面临的错误锁定点的数目更多。特别是在较强的噪声环境、严重的多径或干扰条件下,副峰的幅值甚至会超过主峰,更容易造成环路的错误锁定和模糊跟踪,给用户接收机带来较大测距和定位误差。

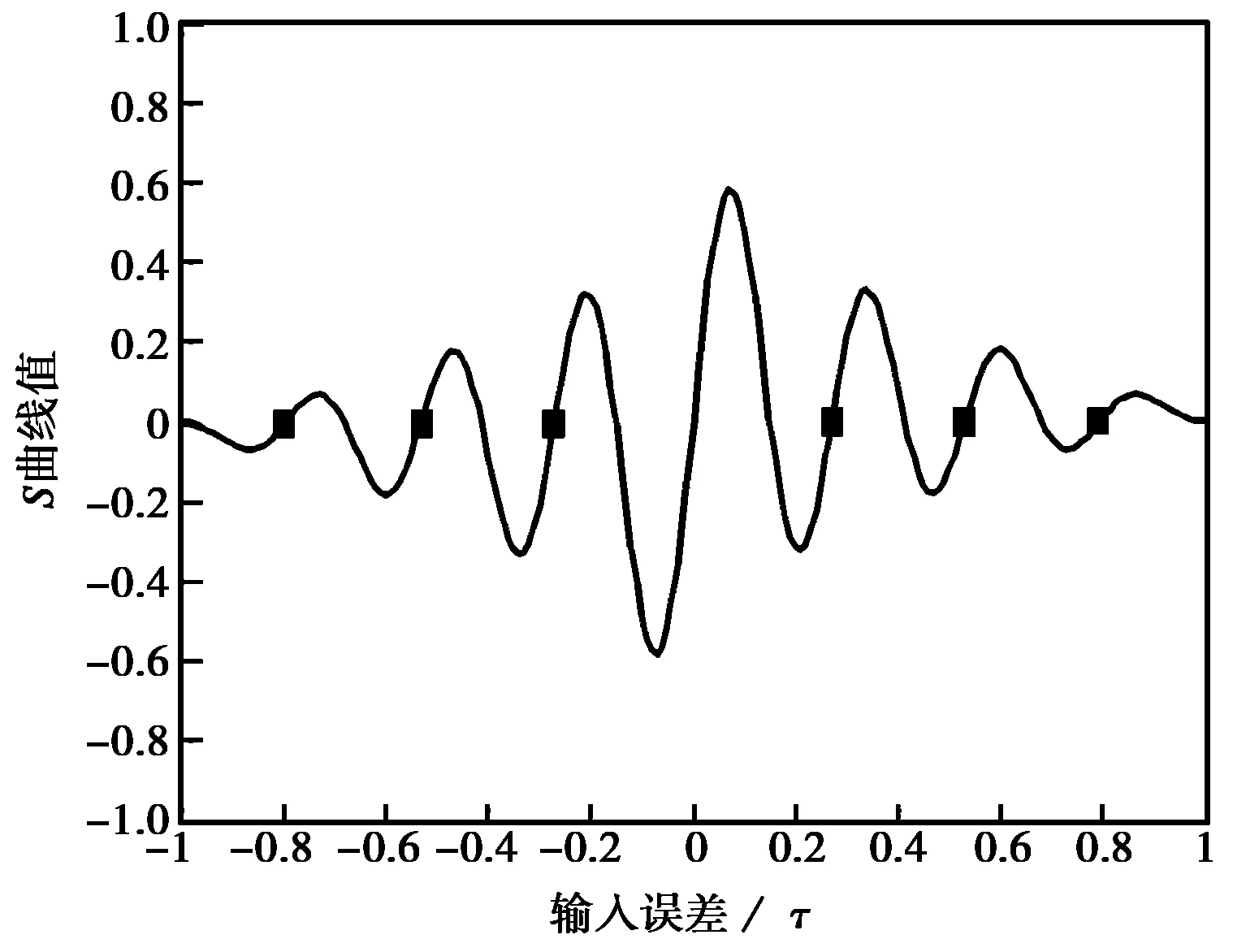
图6 BOC(10,5)信号EMLP鉴别器S曲线

2 高阶BOC调制信号无模糊跟踪技术

高阶BOC信号的的均方根带宽较大,具有较好的跟踪性能,但由于自相关函数存在大量副峰,极易出现错误锁定和模糊跟踪问题,目前提出的主要解决方法有:Bump-Jump算法[3],BPSK-like算法[4],SCPC算法[5]双环路算法[6]。

2.1 Bump-Jump算法

Bump-Jump算法最早由Paul Fine和Warren Wilson提出[3],通过在码跟踪环路原有的超前、即时和延时(E、P、L)支路的基础上增加了两路远超前(VE)、远滞后(VL)支路的本地码,通过当前跟踪的相关峰的幅值(P支路)与邻近的相关峰幅值(VE、VL支路)的对比,进行错误跟踪峰值检测,最终精确跟踪上BOC自相关函数的主峰。Bump-Jump算法的优点是能够充分发挥BOC调制信号主峰较窄,跟踪精度较高的性能优势。对于BOC(2n,n)调制信号,正确锁定主峰的跟踪状态如图7所示。

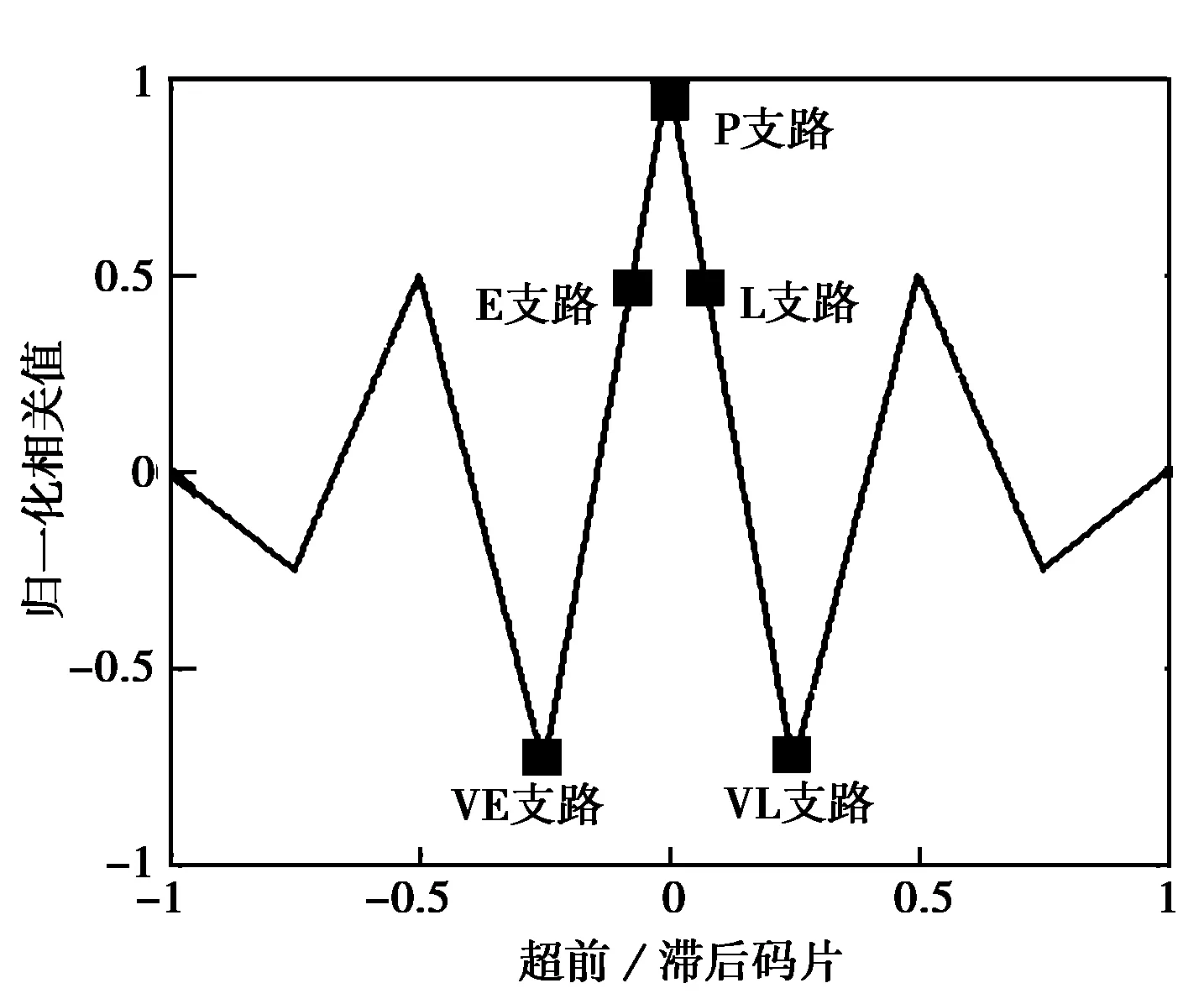
图7 Bump-Jump正确锁定主峰示意图

错误跟踪峰值检测方法为:设置三个计数器分别与VE、P、VL支路相关联。在每一次积分清零周期结束时,比较VE、P、VL三条支路跟踪相关峰的幅值。如果VE支路的值最大,则它对应的计数器加1,同时VL支路的计数器减1;如果VL支路的值最大,则它对应的计数器加1,同时VE支路的计数器减1;如果P支路的值最大,则VE、VL支路的计数器同时减1.计数器的值不小于0.当VE支路或VL支路的计数器超过指定的门限时,跟踪环路跳到该支路指示的相关峰值处。为了克服噪声对相关峰幅值造成的影响,防止把正确跟踪到主峰的状态判断为错误锁定,计数器设定的门限要足够高。

虽然Bump-Jump算法能够实现高精度无模糊跟踪,但因为它是基于相关峰幅值的大小进行检测,当信号载噪比较低、信号遭到破坏、或存在多径干扰的条件下,相关峰形状扭曲变形,将不能检测主峰和副峰。一般的,BOC调制阶数越高,相关函数主峰的幅值和副峰相差越小,相关峰幅值受到上述因素影响越大,同时也将花费更长的时间判断是否正确锁定主峰或者从错误状态调整到准确位置。因此,Bump-Jump算法的有效性仅限于BOC(n,n)、BOC(2n,n)等低阶BOC信号的无模糊跟踪,不适用于BOC(14,2)、BOC(15,2.5)等高阶BOC信号的无模糊跟踪。

2.2 BPSK-like算法

BPSK-like算法[4]是将BOC(m,n)信号近似视为两路中心频率在fcarrier+fs和fcarrier-fs的BPSK-R(n)调制信号的叠加,通过频移和滤波的方法得到仅包含单个主瓣的基带信号,然后与本地生成的BPSK-R(n)信号做相关运算,得到无模糊的相关函数。BOCs(14,2)调制信号视为两路BPSK信号叠加的频谱图如图8所示。

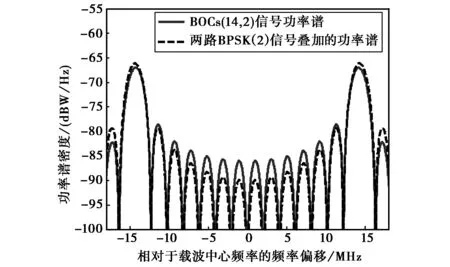
图8 BOCs(14,2)信号视为两路BPSK信号

BPSK-like算法处理后得到的BOCs(14,2)无模糊相关函数如图9所示,其形状与BPSK-R调制信号的自相关函数相似。图中显示了接收机只利用单个主瓣的能量和同时利用两个主瓣能量情况下的相关函数,只利用单个主瓣的能量将会造成至少3 dB的能量损耗,同时利用两个主瓣能量可以减少能量损耗。

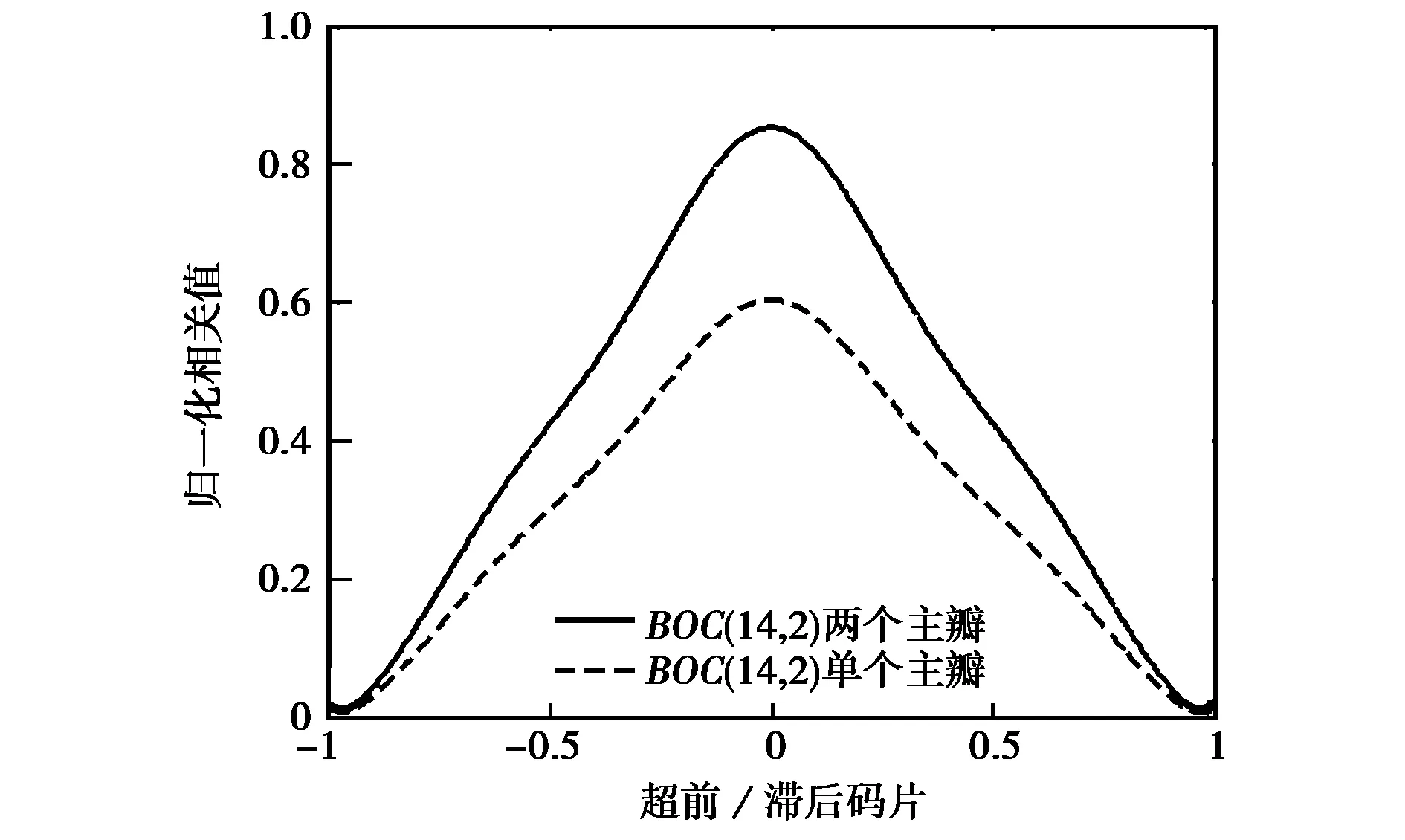
图9 BPSK-like算法得到的无模糊相关函数

BPSK-like算法展宽了相关函数,以削弱BOC信号的跟踪精度和抗多径性能为带代价实现了无模糊跟踪,与Bump-Jump算法相比,BPSK-like算法计算量低,能够快速锁定到主峰,实现简单并可以降低接收机的成本和功耗,适用于高阶BOC信号的接收处理。

2.3 副载波相位消除法

副载波相位消除法(SCPC)[5]使用相互正交的两路本地信号分别与接收信号做相关,利用BOC码与QBOC码的互相关函数的峰值对应于BOC码自相关函数的零点、BOC码自相关函数的峰值对应于BOC码与QBOC码的互相关函数的零点的特点,将两路运算结果进行平方相加,得到无模糊相关函数。BOCs(14,2)信号使用SCPC算法得到的相关函数如图10所示,其中预相关带宽为36 MHz.

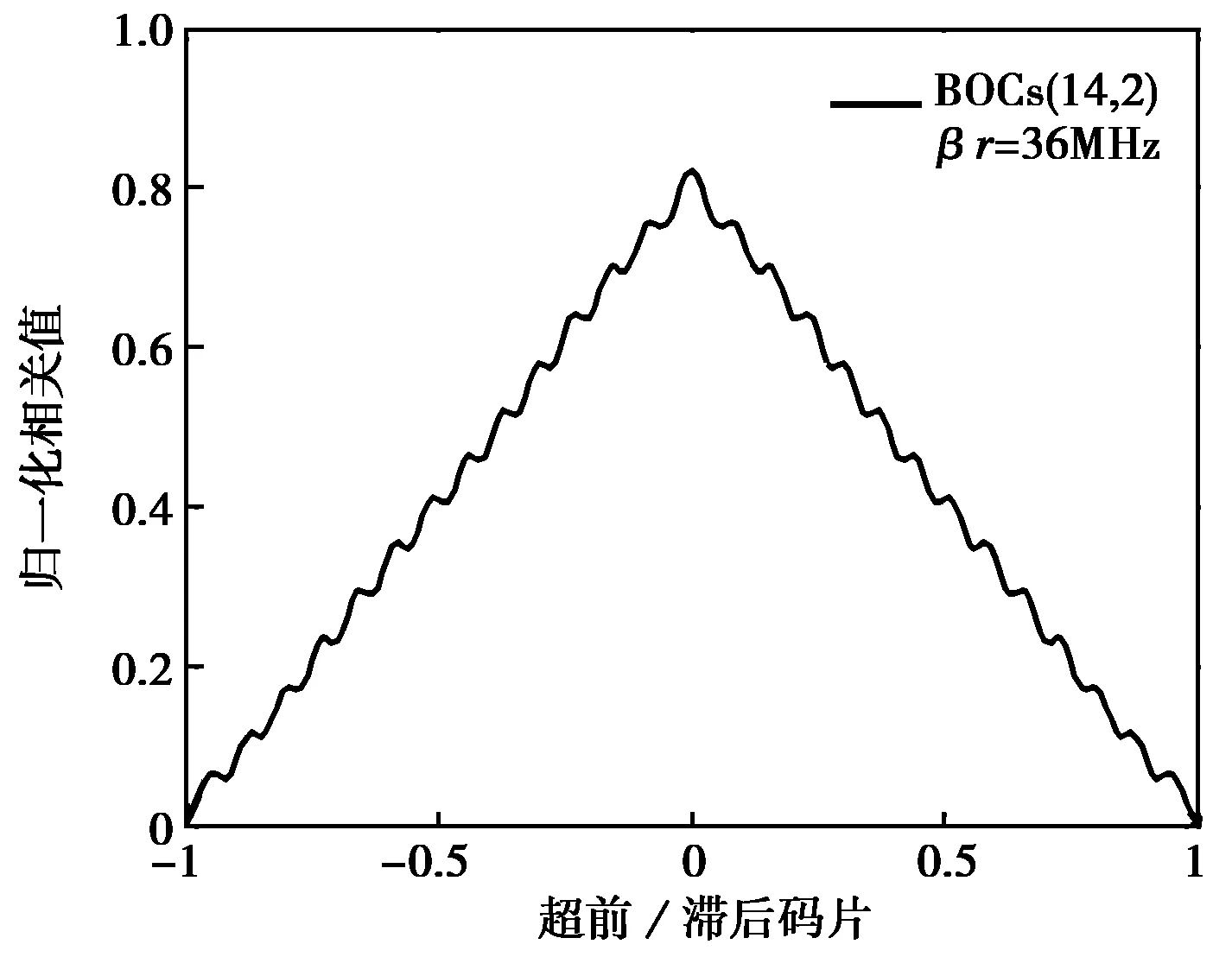
图10 SCPC算法得到的无模糊相关函数

与BPSK-like算法相比,SCPC算法不需要增加滤波器,同样得到的无模糊相关函数。

对于BOC(14,2)信号,预相关带宽为36 MHz,早迟码间隔为0.06码片条件下,使用归一化的非相干超前减滞后功率(EMLP)鉴别器得到的S曲线如图11所示。S曲线在稳定点附近线性区域内的斜率体现了码环对接收信号的码相位跟踪精度,斜率越大,码跟踪误差就越小。由图可知,SCPC算法得到的鉴相器曲线在稳定点附近的斜率比BPSK-like算法大,因此码环的跟踪精度更优。但是,与BOC信号自相关函数的主峰宽度相比,SCPC算法得到的无模糊相关函数顶部展宽,可知SCPC算法和BPSK-like算法一样,未能有效发挥BOC信号的性能优势。

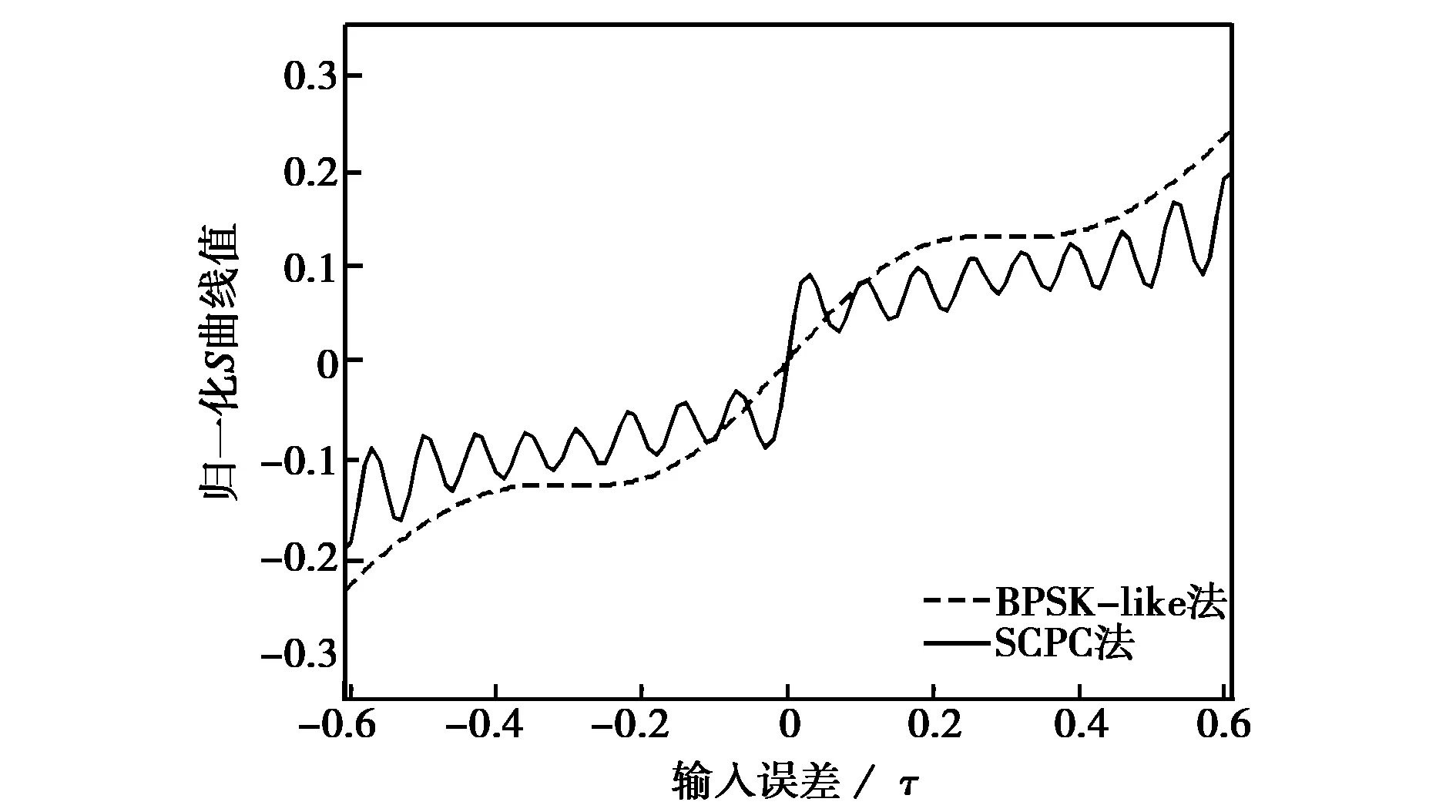
图11 SCPC算法和BPSK-like鉴别器S曲线

2.4 双环路算法

Hodgar和Blunt首先提出在使用延迟锁定环(DLL)跟踪伪码相位的基础上,增加副载波锁定环(SLL)跟踪副载波相位的BOC调制信号无模糊跟踪技术,称为DET或双环路算法[6]。一般认为接收到的BOC信号中调制的副载波和伪码之间的相位关系是确定的,副载波和伪码的相位延迟也是一致的。而使用双环路算法时,突破了这一约束,本地生成信号的副载波相位和伪码相位相互独立,使用SLL和DLL两个环路分别控制。

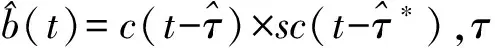
图12 双环路算法二维相关函数

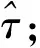
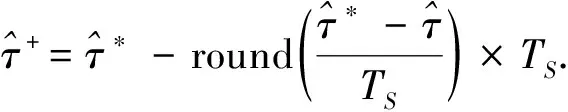
(4)

需要注意的是,当副载波相位没有对齐时,在伪码相位一维,相关函数形状不对称。此时如果DLL环路采用非相干超前减滞后功率(EMLP)鉴别器,得到的S曲线会偏离正常稳定点,如图13所示,其中早迟码间隔Dc为0.2码片,Δ表示方波副载波相位估计误差,TS表示方波副载波半周期长度。采用‘4-point’鉴别器可缓解相关函数不对称造成的S曲线偏离正常稳定点的问题,鉴别器输出可表示为:

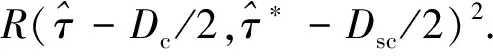
(5)

当DLL环早迟码间隔Dc为0.2码片,SLL环早迟码间隔Dc为0.4子码片时,不同副载波相位误差条件下‘4-point’鉴别器得到的S曲线如图14所示。

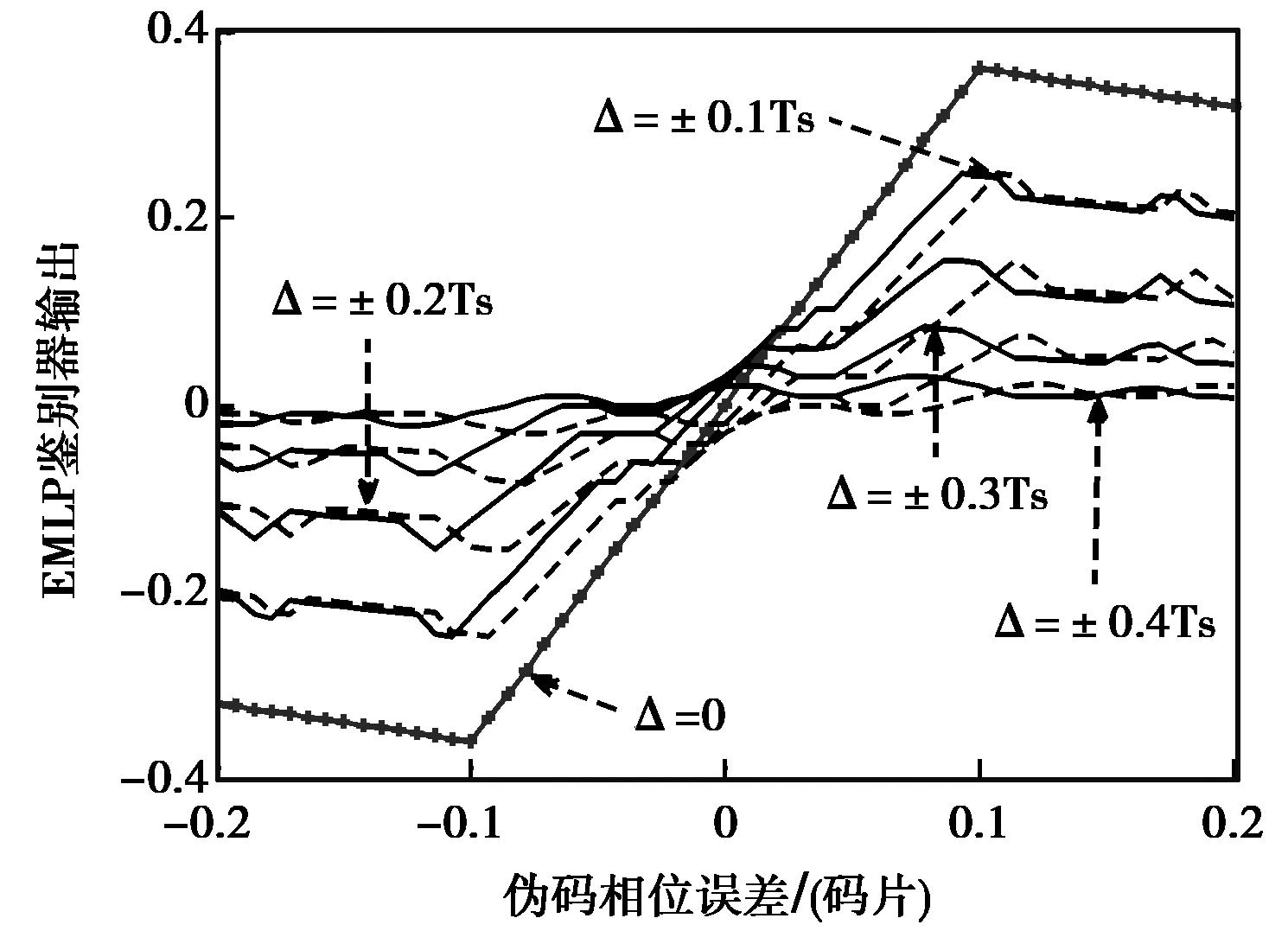
图13 EMLP鉴别器S曲线

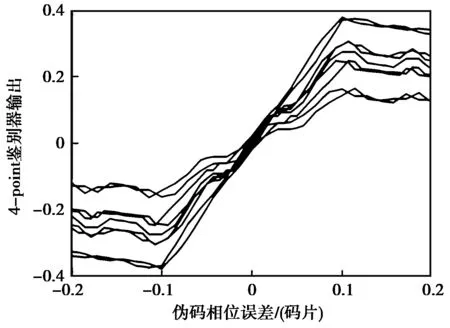
图14 ‘4-point’鉴别器S曲线

与SCPC算法、BPSK-like算法将BOC调制信号多峰的相关函数展宽为无模糊的相关函数不同,双环路算法将其转换为二维的相关函数,并在副载波相位一维保持了BOC信号相关函数主峰较窄的特征,实现了信号的高精度稳定跟踪,已被实际接收机采用[7-8]。

3 性能比较

1)硬件复杂度方面:BPSK-like算法上下两个边带相关运算时要有独立的载波剥离,需要在接收机相关器结构中添加一个本地晶振和增加滤波器资源;双环路算法需要为生成副载波添加一个本地晶振;四种方法所需的乘法器和积分器数量上近似相同。

2)计算复杂度方面:Bump-Jump算法、SCPC算法和双环路算法需要生成副载波,数据速率和计算复杂度高于BPSK-like算法。同时,Bump-Jump算法需要花费更多的计算和更长的时间判断是否正确锁定主峰或者从错误状态调整到准确位置。

3)跟踪精度方面:Bump-Jump算法没有改变BOC信号相关函数的主峰较窄的特征,能够实现高精度跟踪;SCPC算法、BPSK-like算法得到的是展宽的相关函数,削弱了BOC信号的跟踪精度;双环路算法将多峰的相关函数映射成二维相关函数,同样能够实现高精度跟踪。

4)跟踪稳定性方面:Bump-Jump算法跟踪稳定性差,对信号失真和信噪比变化较为敏感,当相关峰形状扭曲变形时,可能发生错锁,产生较大测距误差。双环路算法在信噪比较低或存在多径干扰时,仍能够经过校正保持稳定跟踪。

综上所述,双环路算法在跟踪精度方面接近理论性能,并且不会面临Bump-Jump频繁校正的问题,双环路算法的硬件复杂度和计算复杂度也较低,是较好的高阶BOC信号跟踪方案。另外,双环路算法的跟踪环路结构与传统接收机的环路结构相比,仅增加了副载波锁定环,经过调整后也可用于传统的BPSK-R信号的接收,应用灵活性强。

4 结束语

各大卫星导航系统广泛采用了BOC调制方式,本文主要描述了BOC调制信号的特征,对常见的几种无模糊跟踪算法在高阶BOC信号跟踪时的有效性进行了分析和比较。其中,Bump-Jump算法不适用于高阶BOC信号的无模糊跟踪;BPSK-like算法计算复杂度低,削弱了BOC信号的跟踪性能;双环路算法实现了无模糊跟踪,并且跟踪精度高、跟踪稳定性好。高阶BOC信号占用的频带较宽,上述跟踪算法在非理想条件下的有效性是下一步研究的重点。

[1]BETZ J. Something old, something new-signal structures for satellite-based navigation:past, present, and future[J].Inside GNSS, 2013,8(3):34-42.

[2]BETZ J W, Design and performance of code tracking for the GPS M code signal[C]//Proceedings of ION GPS-2000, Institute of Navigation, 2000.

[3]FINE P, WILSON W.Tracking algorithm for GPS offset carrier signals[C]//Proceedings of the National Technical Meeting of the Institute of Navigation, 1999: 671-676.

[4]MARTIN N, LEBLOND V, GUILLOTEL G,etal. BOC (x,y)signal acquisition techniques and performance [C]//Proceeding of ION 2003:188-198.

[5]WARD P W.A design technique to remove the correlation ambiguity in binary offset carrier (BOC)spread spectrum signals [C]//Proceedings of U.S. Institute of Navigation NTM Conference, 2004: 886-896.

[6]HODGART M S, P.D. BLUNT P D, UNWIN M.Double estimator: A new receiver principle for tracking BOC signals[J]. Inside GNSS, 2008,3(3):26-36.

[7]RUEGAMER A, SUBERVIOLA I, FOERSTER F, et al, “A bavarianInitiative towards a Robust Galileo PRS receiver[C]//ION GNSS 2011:3668-3678.

[8]HODGART M,ODGART S, SIMONS E. Improvements and additions to the double estimation technique[C]//Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), 2012 6thESA Workshop, IEEE,2012.