基于ASP逻辑的偏好多语境系统

王淑庆

（南京大学哲学系，江苏南京210046）

一、背景与动机

多语境系统（Multi-Context System，简写为MCS）的形式化研究始于1994年，当时Giunchiglia等人把它叫做多语言层级逻辑[1]。2001年，Giunchiglia等人针对MCS给出了一种不同于可能世界语义学的局部模型语义学[2]。2004年，Roelofsen等人从算法的角度研究了多语境系统的可满足性问题[3]；2005年他们又把非单调推理引入MCS，给出了非单调的MCS[4],并在2007年把它进一步发展为多语境缺省逻辑[5]。2007年，Brewka等人提出一种能刻画单调与非单调MCS的统一形式框架[6]。目前，MCS在各种分布式系统中得到了许多应用，比如自然语言分析、机器人、搜索引擎、CYC、语义网、多主体系统、常识推理……另外，它还被认为在下一代AI“普遍性问题”[7]的应用发展中起着重要作用，比如环境智能。

现有的MCS，不管是单调的还是非单调的，各语境之间的信息交流都通过桥规则这个“通道”。但是，现有的MCS很少考虑给出规则间或语境间的偏好关系及其语义。因此，在MCS中加入各种偏好关系并且给出严格语义，可以说是对MCS非常自然的扩充。

另一方面，现有的非单调MCS的桥规则“天然地”具有增加知识或信息的能力，而没有删除信息的功能。对于单调的MCS来说，已有的事实或信息当然是“不可动摇”的；但是，对于非单调的MCS来说，删除信息应该和增加信息一样具有“平等的地位”，而且正是因为删除信息而更能体现出它的非单调性。虽然Brewka等人通过托管的方法实现了命令式删除[8]，但过于复杂而且不是逻辑式删除（陈述式删除）。

受偏好ASP[9]和信念修正AGM[10]的启发，本文在MCS的桥规则的头部加入各种偏好关系，通过其偏好语义来阻止某些规则的使用，进而实现逻辑删除功能。这是一种比较自然的想法，之所以要删除某些信息，很大的原因就在于偏好及其变化。

二、预备知识

2.1 ASP逻辑

ASP（Answer Set Programming）是一种非单调逻辑编程，它的语法只是在Prolog的基础上增加了缺省否定和经典否定，语义则是基于极小厄布朗模型[11]。ASP虽然无法计算所有的递归函数，但足以对NP完全问题进行编码，而且它在许多复杂的组合计算问题上具有相当的表达力和推理能力。目前，ASP在密码分析、模型检测、AI规划、优先推理[12]、语义网、航天飞机的高水平控制等领域都有不少应用。

本文把用ASP语言写的程序称作ASP程序，具体有很多种，下面仅介绍一般逻辑程序GLP。

（1）GLP语法

定义2.1：GLP为形如规则R0的非空有限集合，R0形为：

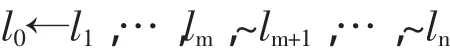
其中，l0∈Lit∪{⊥}，Lit为所出现的命题文字集，li∈Lit（i≥1），～表示缺省否定。head（R0）=l0，body（R0）=l1，…，lm，～lm+1，…，ln，body（R0）+=l1，…，lm，body+（R0）={ll，…，lm}，body-（R0）={lm+l，…，ln}。R0读作：如果有l1…且lm，而且没有lm+l…且没有ln，则有l0。显然，R0形式的规则就是“如果……，那么……”的形式，只不过它允许缺省文字作为前提，从而可以实现非单调推理。

（2）GLP语义

逻辑程序的语义在表现形式上主要有三种：模型论语义、不动点语义以及执行语义。下面给出GLP的模型论语义。

定义 2.2：设∏是一个 GLP 程序，令 X⊆Lit，∏的 X 归约程序∏X={head（R0）←body（R0）+|R0∈∏，body-（R0）∩XØ}，如果X等于∏X的极小厄布朗模型，则称X是∏的回答集。

下面介绍人工智能中的一个“逻辑”概念。

定义 2.3：一个逻辑 L=（KBL，BSL，ACCL），其中，KB 是一个知识库（公式集）的集合；BS 是可能的信念集的集合；ACC是从KB到2BS的一个函数，它把KB的每个元素对应到它的可接受的信念集的集合。

在上面的“逻辑”定义中，ACCL其实就是L的语义刻画函数[6]，它刻画了“某个逻辑”的“后承关系”。这种对“逻辑”的定义是基于“输入-可能的状态-输出”的模式，非常适用于多种应用逻辑。比如描述逻辑和ASP逻辑。

2.2 多语境系统MCS

下面介绍Brewka等人给出的非单调多语境系统[6]。非单调MCS在单调MCS上加入非单调推理的因素，包括非单调的逻辑和非单调的桥规则。

（1）语法

定义 2.4：设 L={L1，…，Ln）为 n 个逻辑的集合，L 的一个 Lκ-桥规则形如：

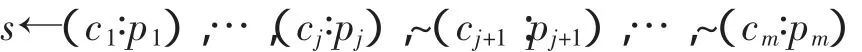
其中，1≤cκ≤n，表示第cκ个语境，pκ是Lcκ的某些信念集的元素，且对于每个 kb∈KBκ∶kb∪{s}∈KBκ。

定义2.5：一个非单调多语境系统MCS=（C1，…，Cn），其中Ci=（Li，kbi，bri），Li=（KBi，BSi，ACCi），kbi∈KBi，bri是{L1，…，Ln}的Li-桥规则的集合，其中的局部推理具有非单调性或者具有非单调的桥规则。

可见，多语境系统是多个语境的收集，其中每个语境抽象为包含逻辑和知识库以及桥规则的三元组，每个语境通过桥规则这个“通道”联系其他语境。

定义 2.6：设 M=（C1，…，Cn）是一个 MCS，它的一个信念状态 S=（S1，…，Sn），其中每个 Si∈BSi。

定义 2.7：一个桥规则r∈br在一个信念状态 S=（S1，…，Sn）中是可应用的，记为S ⊨body（r），当且仅当，body+（r）|cκ⊆Scκ，且body-（r）|cκ∩Scκ=Ø，即对1≤i≤j有pi∈Sci且对j+1≤k≤m有pκ∉Scκ。

（2）语义

MCS的语义即给出各个语境都能接受的知识或信息。从推理的角度上来说，一旦给定一个MCS，那么各语境都能接受的东西就是它能推出的东西，从而就可以把MCS的语义看作一个均衡。

定义2.8：一个信念状态S=（S1，…，Sn）是MCS的一个均衡，当且仅当，以下条件成立：

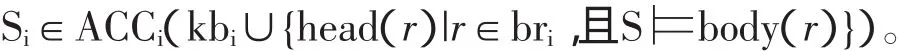
一般来说，任给一个多语境系统，它是否有均衡是要通过计算才能得出的。如果没有均衡，则认为它不一致，由此引出MCS不一致性的定义。

定义2.9：一个MCS是不一致的，如果它没有均衡。

例子 2.1：设 M=（C1，C2，C3，C4）是一个 MCS，它表示一个医疗决策的专家系统，其中：

C1∶L1=经典逻辑，kb1={小王对抗生素强过敏}，br1=Ø；

C2∶L2=经典逻辑，kb2={血标记者，X 射线诊断有肺炎}，br2=Ø；

C3∶L3=描述逻辑，kb3={典型性肺炎≡肺炎 血标记者}，br3={小王是血标记者←（2：血标记者），小王有肺炎←（2：X射线诊断有肺炎）}；

C4∶L4=ASP逻辑，kb4={给药∨打针←需要抗生素；给药←需要强的；⊥←给药，～允许强的；什么也不需要←～需要抗生素，～需要强的}，br4={需要抗生素←（3：小王有肺炎）；需要强的抗生素←（3：小王有典型性肺炎）；允许强的←～（1：小王对抗生素强过敏）}。

因为语境2中有“血标记者”和“X射线诊断有肺炎”，所以br3中两条桥规则都可用；同理易知，br4的前两条也可用，从而与语境1矛盾，所以M是不一致的。

三、基于ASP逻辑的偏好多语境系统

本文在MCS的桥规则头部加入两种二元偏好关系：从桥规则身躯有无条件上来看，分为条件偏好和绝对偏好；从偏好的本身属性上来说，又分为语境偏好和规则偏好。

3．1 PMCS 的语法

定义3.1（条件偏好）：MCS上的一个条件偏好是指如下形式的R1：

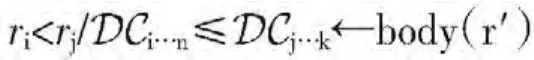
其中，ri形如R0，rj形如R0或为空串；表示任意不同语境的组合；r′∈b（r桥规则集）；/意指“要么”。

定义3.2（绝对偏好）：MCS上的一个条件偏好R1，如果body（R1）不存在，则称它为一个绝对偏好，记为R2：

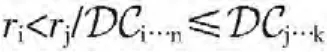
其中，ri＜rj叫做规则偏好，其实就是命题间的偏好；叫做语境偏好，也就是世界间的偏好。R1和R2统称为偏好桥规则，语境i中的偏好桥规则的集合记为pbri。把偏好桥规则的第一个头记为head1（R），第二个头记为head2（R），一般的头记为head（R）。

由此可见，偏好桥规则的身躯带有语境性的条件。在我看来，“偏好”多数情况下是具有条件性和语境依赖性的。

用Gi1表示局部非桥规则集，Gib表示局部桥规则集。在以上定义的基础上，就可以统一给出带偏好的多语境系统的语法。

定义3.3：一个偏好多语境系统PMCS=（C1，…，Cn），其中每个Ci=（Li，Gi，Pi），Li=（KBi，BSi，ACCi），Gi=Gi1∪Gib（局部非桥规则集和局部桥规则集的并），Pi=pbri。

显然，MCS可以看作是PMCS的每个Pi都为空集的情况，所以MCS在语法上就是PMCS的特例。

定义3.4：一个基于ASP逻辑的偏好多语境系统是一个PMCS，如果其中的每个Ci里的逻辑Li都为ASP逻辑。

由此可见，PMCS和MCS的区别就在于偏好桥规则集上，显然，这些桥规则集上的偏好关系有不同的层次。因此，要给出基于ASP逻辑的PMCS的语义，也只能区分对待不同层次的偏好关系。

3.2 PMCS的语义

要给出PMCS的完整语义，目前看起来是非常困难的，因为它既要考虑不同的逻辑对偏好的影响，又要考虑规则偏好和语境偏好对语义的影响，而偏好本身又不是一个单纯的概念。假定PMCS中各语境的逻辑都是ASP逻辑，则可以比较好地来处理PMCS中的偏好语义。下面用M表示任意基于ASP逻辑的偏好多语境系统PMCS。

一个偏好规则集的头组成的集合里不存在规则ri使得有ri＜rj＜…＜ri成立的情况，则称它是良性的。否则是非良性的。下面给出信念状态S相对于偏好桥规则集pbri上的偏好关系集pref（pbri）的定义。

定义3.5：设一个信念状态S=（S1，…，Sn），则相对于S的pref（pbri）={head（r′）|S⊨body（r′），且head（r′）组成的集合是良性的，r′∈pbri）。

此定义的直观意义是：如果S满足r′的躯干上要求的所有条件且不会导致非良性，则可以把r′的头部添加到pref（pbri）中去。在pref（pbri）的基础上，就可以分层次地给出PMCS的语义。

定义3.6：一个信念状态S=（S1，…，Sn），若相对于S的pref（pbri）={x|x∈pref（pbri），且x为规则偏好}，则S是M的一个均衡，当且仅当，对1≤i≤n，以下条件成立：

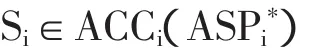
其中，ASPi*=ASPi-{ri|存在ri∈ASPi，存在rj∈{head2（r′）}或rj为空串使得ri＜rj，r′∈pbri}∪{rk|存在ri∈ASPi，使得ri＜…＜rk且无rk＜rk+1使rk+1所在的r″对 S 可用且良性，r″∈pbri，rj，rk，rk+1为空串或形如 R0}。

这里语义的直观思想是：若一个偏好桥规则r′对S可用，且没有比它的第二个头更优先的头所在的偏好桥规则r″对S可用，而且r′的第一个头属于ASPi，则可把r′的第二个头即规则rj添加到原程序中去；若有比rj更优先的链存在的话，则只需要把链的最后一个元素加进来；同时减去ri。这样就把有序的程序化为无序的ASP程序，化归后它的语义就和一般的ASP无异。因此，也很容易给出它的模型论语义或不动点语义，在此省略。

一个文字如果是由若干条可用的桥规则或偏好桥规则共同得到的，那么这些规则的躯体中语境位置出现过的所有语境的组合称为导出语境体（用表示），这个文字叫做此语境体的导出文字（用dl表示）；若这些规则有不可用的，则称这个文字为此语境体的可能导出文字。特别地，一个语境是它的任意回答集中的任一文字的导出语境体。一个文字lh依赖于文字li是指：无li则无lh。

定义3.7：设一个信念状态S=（S1，…，Sn），且相对于S的pref（pbri）非空，则信念状态S是M的一个均衡，当且仅当，以下条件成立：

可见，语境偏好对语义的影响与规则偏好有些不同，不过它最终也还是要通过删除某些文字来证明它的存在性。具体来说：假定M在无偏好时有均衡，且考虑语境偏好时，M并没有冲突，则语境偏好不起作用；若产生了不一致，则先寻找那些导致不一致的成对的导出语境体（不一致一定是因为两个语境体导出了相反的文字），再看它们有无可用的偏好关系——若无，则偏好不起作用，M没有均衡；若有，就只“相信”最偏好的那个语境体所导出的文字。

3.3 一个例子

下面举一个简单的例子来说明PMCS是如何进行推理的。

例子 3.1：设 M=（C1，C2，C3，C4）是一个 PMCS，四个语境分别表示有点敌对关系的两个员工以及他们的两个上司，其中：

C1：L1=ASP 逻辑，R1={高兴；去改变←不高兴}，P1={高兴＜不高兴←～（2：工作）；（去改变←不高兴）＜（不改变←不高兴）←～（2：工作）}；

C2：L2=ASP 逻辑，R2={可接受←不好，～不可接受；工作←（1：去改变）；不好←～（1：不高兴）；工作←（3：让 2工作），～（1：高兴）；不工作←（4：让 2不工作）；工作←（1：不高兴）}，3：让 2工作），（4：让 2不工作），～（1：高兴）}；

C3：L3=ASP 逻辑，R3={工作；让 2 工作}，P3=Ø；

C4：L4=ASP 逻辑，R4={不工作；让 2 不工作}，P4=Ø。

我们先来分析一下这四个语境。首先，1中有一个信息是“高兴”，但是有一条偏好桥规则又说了如果2“工作”则1会偏好于“不高兴”；1中还有一个规则是“去改变←不高兴”，但又有一条偏好桥规则说如果没有2“工作”则“不高兴则不用去改变”；2中第三条偏好桥规则是说如果3和4分别都让2“工作”和“不工作”且1中无“高兴”，则它偏好导出语境体的其他规则好理解；3和4基本上就是要求2和自己所做的事一样。

由以上分析，再根据PMCS的语义，则有：

1）假设1里确实接受“高兴”，则2中第三条偏好桥规则不可用，同时2中第4条桥规则也不可用；另外2里会接受“不好”，再接受“可接受”，这样易知此PMCS有以下一个均衡：

·E1=（{高兴}，{不工作，不好，可接受}，{工作，让 2 工作}，{不工作，让 2 不工作}）。

2）同理，假设2中有“工作”，则1中第一条偏好桥规则可用，从而“高兴”应该从1中删除而代之以“不高兴”；由于此时1中第二条偏好桥规则不可用，故根据“去改变←不高兴”，可得“去改变”也是1中应该接受的；另外，2中只有第二和第四条规则不可用；最后，3和4中的都是事实，所以此PMCS还有以下一个均衡：

·E2=（{不高兴，去改变}，{工作}，{工作，让 2 工作}，{不工作，让 2 不工作}）。

由此可见：

1）在E1中，语境1中第一条偏好桥规则通过规则偏好删除了1中的一个“事实”，但第二条桥规则没有发挥作用。

2）在E2中，语境2中的偏好桥规则通过语境体偏好删除了语境4流入的信息。

四、删除功能与处理不一致性

4.1 删除功能

4．1．1偏好桥规则的删除功能——通过规则偏好

通过规则偏好来删除某些信息比较简单，比如说，要删除某个语境中的规则ri，只需要在某个桥规则的头部中加入其他规则（比如要删除的文字或规则的否定）或者空串，然后在偏好桥规则的身躯加入一些应该满足的条件，根据PMCS的语义，就能够实现偏好桥规则的删除功能。具体来说，即加入以下形式的偏好桥规则于某个语境中：

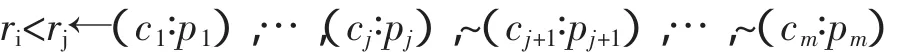
由PMCS的语义我们可以知道，rj或﹁ri可能会添加到某个语境的知识库中去，但如果rj是空串的话，则它只是起到阻止ri的作用。不管它们是加入到知识库中去，还是仅仅发挥了阻止作用，结果上都能实现删除的功能。

4．1．2偏好桥规则的删除功能——通过语境偏好

除了规则偏好能实现删除功能外，语境偏好也可以实现之：先看冲突文字在哪些导出语境体之间，再在桥规则的头中加入要删除的文字的语境体偏好，然后在偏好桥规则的躯体部加入一些应该满足的条件。即加入以下形式的偏好桥规则于某语境中：

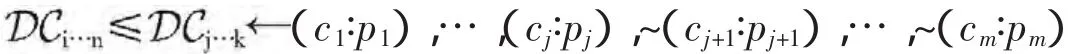
显然，语境偏好并不像规则偏好那样“比较直接地”实现删除，而是“转个弯”通过语境体的偏好而阻止了其他语境体导出文字的使用，从而实现删除功能。

例子 4.1：设 M=（C1，C2，C3）是一个 PMCS，三个语境分别表示两女一男，其中：

C1：L1=ASP 逻辑，R1={不愉快；去喝酒←愉快}，P1={不愉快＜愉快←（2：成功）；（去喝酒←愉快）＜（不改变←不愉快）←～（2：成功）}；

C2：L2=ASP 逻辑，R2={不愉快←（1：去喝酒）；不好←（1：愉快）；愉快←（3：让 2愉快）；成功←～（1：成功）}（3：回家），～（1：非常愉快）}；

C3：L3=ASP 逻辑，R3={回家；让 2 愉快}，P3=Ø。

“不愉快”是1中的“事实”，然而1中有一条偏好桥规则可能阻止它成为事实（即从愉快转变为不愉快）；同理可以分析1的另外一条偏好桥规则可能阻止1中的“去喝酒←愉快”的成立。但由于1的两条偏好桥规则只有一条可用，故只可以删除1中的一条信息。

另外，若无语境偏好关系，则M无均衡。但由于2中的偏好桥规则可以成立，故，后者阻止了前者的信息即“愉快”的流入，即相当于把本来要加入的东西删除了。所以，M有一个均衡：

·E=（{愉快，去喝酒}，{不愉快，成功}，{回家，让 2 愉快}）。

4.2 处理不一致性

MCS可能没有均衡，即各个语境之间可能出现不一致的情况。不一致产生的原因比较复杂，毕竟不同的语境中可以有不同的语言、不同的逻辑以及不同的知识和不同的桥规则。但是，我们可以通过诊断和解释的办法找到MCS的不一致之处[13]。

用pbrM表示一偏好多语境系统M的所有偏好桥规则的集合，R⊆pbrM，M［R］⊨⊥表示M在有R的情况下没有均衡，M［R］⊨/⊥表示相反。dl（R）表示R的导出文字对（增加的文字用正文字表示，删除的文字用负文字表示）的集合，M［R′+dl（R″）］⊨⊥表示M在有R′和dl（R″）作用于M（即把正的文字增加到M相应语境中去，把负的从M相应语境中删除）的情况下M没有均衡。

定义4.1：给定一个偏好多语境系统M，M的不一致性的诊断是一个有序对（D1，D2），其中D1，D2⊆pbrM，并使得对于所有的（R′，R″）（D1⊆R′⊆pbrM，且R″⊆pbrMD2），M［R′+dl（R″）］⊨⊥。用D±和D±m（M）分别表示M的所有不一致诊断和极小不一致的诊断的集合。

D1直观上就是说，M［D1］会导致和M相关的不一致；D2的直观意思是，D1并不能无条件地导致不一致，因为dl（D2）可能可以修复它的不一致。

定义4.2：给定一个偏好多语境系统M，M的部分一致的解释是一个有序对（E1，E2），且E1，E2⊆pbrM，并使得M［pbrME1+dl（E2）］⊨/⊥。用E±和E±m（M）分别表示M的所有部分一致的解释和极小部分一致的解释的集合。

部分一致的解释直观的意思是说，如果把E1去掉，且把E2的导出文字对集拿来，则会有均衡。也就是说，如果没有E1，且E2可用，则M有均衡。

M的部分一致的解释和不一致性的诊断之间，有以下定理：

定理 4.1：任意一个偏好多语境系统 M，有∪D±m（M）=∪E±m（M）。

证明思路：此证明非常复杂，具体和文献[13]中给出的证明思路类似。

五、结论与展望

为了在MCS中表达语境依赖性和条件依赖性的偏好信息以及实现MCS桥规则的删除功能，本文在现有的非单调MCS的基础上提出了一种偏好多语境系统PMCS：给出了PMCS一般的语法，并给出了基于ASP逻辑的PMCS的语义；然后运用PMCS处理了两个问题，即PMCS的桥规则的删除信息问题与PMCS的不一致性问题。

本文没有给出PMCS的一般语义，也没有对PMCS的元性质进行研究，同时也没有考虑动态MCS[14～15]的偏好问题，而本文所做的实际上就是在处理带偏好的MCS的动态均衡问题。因此，这些问题还有待进一步研究。

[1]F．Giunchiglia，L．Serafini．Multilanguage hierarchical logics，or：how we can do without modal logics[J]．Artificial Intelligence，1994，65（1）：29～70．

[2]C．Ghidini，F．Giunchiglia．Local Models Semantics，or contextual reasoning=locality+compatibility[J]．Artificial Intelligence，2001，127（2）：221～259．

[3]F．Roelofsen，L．Serafini，A．Cimatti．Many hands make light work：localized satisfiability for multicontext systems[M]//Proc．of the 16th Eureopean Conference on Artificial Intelligence．Amsterdam：IOS Press，2004，58～62．

[4]F．Roelofsen，L．Serafini．Minimal and Absent Information in Contexts[M]//IJCAI，2005，558～563．

[5]G．Brewka，F．Roelofsen，L．Serafini．Contextual Default Reasoning[M]//IJCAI，2007，268～273．

[6]G．Brewka，T．Eiter．Equilibria in heterogeneous nonmonotonic multi-context systems[M]//AAAI 2007，Menlo Park：AAAI Press，2007，385～390．

[7]J．McCarthy．Generality in Artificial Intelligence[J]．Communications of the ACM，1987，30（12）：1030～1035．

[8]G．Brewka，T．Eiter，M．Fink，A．Weinzierl．Managed Multi-Context Systems[M]//IJCAI，2011，786～791．

[9]K．Wang，L．Zhou，F．Lin．Alternating fixpiont theory for logic programs with priority[M]//Proc．Int’l Conference on Computational Logic，Springer-Verlag，2000，164～178．

[10]C．E．Alchourrän，P．Gärdenfors，D．Makinson．On the Logic of Theory Change：Partial Meet Contraction and Revision Functions[J]．Symbolic Logic，1985，50（2）：510～530．

[11]M．Gelfond，V．Lifschitz．The stable model semantics for logic programming[M]//R．Kowalski，K．Bowen．Proc．of the 5th International onference and Symposium on Logic Programming，Volume 2，Seattle，Washington：The MIT Press，1988，1070～1080．

[12]Z．Yan．Two results for prioritized logic programming[J]．Theory and Practice of Logic Programming，2003，3（2）：223～242．

[13]T．Eiter，M．Fink，P．Schüller，A．Weinzierl．Finding explanations of inconsistency in multi-context systems[J]．Artificial Intelligence，2014，216：233～274．

[14]M．Dao-Tran，T．Eiter，M．Fink，T．Krennwallner．Dynamic Distributed Nonmonotonic Multi-Context Systems[M]//G．Brewka，V．Marek，M．Truszczynski．Nonmonotonic Reasoning，Essays Celebrating its 30th Anniversary，volume 31 of Studies in Logic．London：College Publications，2011，63～88．

[15]G．Brewka．Towards Reactive Multi-Context Systems[M]//Pedro Cabalar，Tran Cao Son．Logic Programming and Nonmonotonic Reasoning．Berlin Heidelberg：Springer，2013，1～10．