基于Sheorey岩体强度准则对等效Mohr-Coulomb强度参数的推导

，

(中国电建集团 贵阳勘测设计研究院，贵阳 550081)

1 研究背景

为了定量描述岩体的强度从而更恰当地评价岩体的稳定性，许多学者都做了大量工作，提出了很多岩体强度准则[1-9]。这些强度准则在描述岩体强度方面各有利弊，总的看来，Mohr-Coulomb(M-C)准则由于其理论简单实用，原理清晰，所需参数不多，虽然更适宜于描述土体等散体介质的强度，但在描述岩体的剪切破坏即抗剪强度方面仍然具有很好的适用性，是工程界应用最为普遍的强度准则。因此，很多商业工程软件内置的强度破坏准则仍然是基于M-C准则，因此在应用其他强度准则时，常常需要获得相应的M-C准则等效强度参数。一些学者在非线性强度准则线性化及推求等效强度参数方面都做出了很有价值的工作[10-12]。本文在介绍Sheorey强度准则的基础上，应用最小二乘法推导了相应的等效M-C强度参数，给出了等效强度参数的通用表达式。

2 Sheorey强度准则

Sheorey准则是一个经验强度准则，由P.R.Sheorey等[13-14]根据煤的室内三轴试验总结归纳而来，也被广泛用于节理岩体的强度与稳定性分析。该准则基于Bieniawski于1976年提出的岩体分级系统(RMR)，通过对岩块的室内三轴试验强度参数进行折减来确定相应原位岩体的强度参数。Sheorey准则在σ1-σ3平面的关系为

(1)

式中：σ1，σ3分别为大、小主应力；σcm，σtm分别为原位岩体的单轴抗压及抗拉强度；bm为表征岩体级别的参数，受岩体的RMR值控制。σcm，σtm和bm可由以下3式确定：

(2)

(3)

bm=bRMR/100。

(4)

式中：σc，σt分别是完整岩块的抗压强度及抗拉强度；RMR是Bieniawski提出的岩体分级系统值；b是表征岩块强度的参数，其值由岩块的室内三轴试验结果统计得到。Sheorey准则是基于煤的室内三轴试验参数而提出来的，在将其应用于岩体时，需与1976年Bieniawski的岩体分级系统联系起来，首先必须取得岩体的RMR值以及完整岩块的室内力学试验参数，将岩块强度参数折减得到岩体强度参数从而应用该准则。

3 推求等效M-C强度参数

Sheorey准则和M-C准则在σ1-σ3平面上的图形如图1所示，根据文献[8]，推求相应于Sheorey准则的等效M-C强度参数,即等效黏聚力c′和等效内摩擦角φ′值应在确定的小主应力σ3区间内进行，其原理是用线性M-C强度包线拟合Sheorey准则，当M-C包线切取Sheorey准则包线所形成的上下部分区域面积相等时的M-C包线c′和φ′值,即为所推求的等效强度参数值。

图1 Sheorey准则和等效M-C准则大、小主应力关系

用于拟合的线性M-C强度包线可表示为

σ1=K0σ3+C0。

(5)

式中K0和C0均为常数，可将其表达为等效M-C强度参数c′和φ′的函数形式，即：

(6)

(7)

只要求出K0和C0的值，即可得到c′，φ′的值。为确定等效M-C强度参数，首先需要确定小主应力σ3的区间，在此区间内推求相应的等效强度参数。该区间的上、下限小主应力值分别记为σ3max，σ3min，一般来说，下限值σ3min取岩体抗拉强度σtm，即σtm<σ3<σ3max，而上限值σ3max应根据不同情况加以分别确定[8]。

使M-C包线切取Sheorey准则包线所形成的上下部分区域面积相等，应用最小二乘法理论，该条件等价于构造一差的平方和函数S，并使该函数取得极小值。在这里S为两准则关系式函数之差的平方在小主应力区间[σ3min,σ3max]的积分，即

(8)

式(8)可以进一步写为

(9)

又

(10)

进一步展开式(10)，可以得到

(11)

联立式(9)至式(11)，有

S=S1+S2-S3-S4+S5。

(12)

式S中仅含有未知变量K0和C0，为求得使S取得极小值的条件，将S分别对2个变量K0和C0求偏导数，并使导数为0。S对C0求偏导得到

(13)

其中：

(14)

(15)

(16)

(17)

(18)

将式(14)至式(18)代入式(13)，并使其等于0，简化后得到

K0+BC0=A。

(19)

式中A，B均为常数，其表达式如下：

(20)

(21)

将S对K0求偏导数，得到

(22)

其中：

(23)

(24)

(25)

(26)

(27)

将式(23)至式(27)代入式(22)，并使其等于0，简化后得到

(28)

式中C，D均为常数，其表达式如下：

(29)

(30)

联立式(19)与式(28)，即得到K0与C0的解:

(31)

K0=A-BC0。

(32)

将式(31)、式(32)代入式(6)与式(7)，得到等效M-C强度参数c′，φ′值：

(33)

(34)

4 不同准则等效强度参数对比分析

为验证上述推导过程以及Sheorey准则的可靠性，本节中列举一实例对等效强度参数进行计算，并将计算结果与Hoek-Brown准则的等效强度参数进行比较分析。

Hoek-Brown准则在最大、最小主应力平面上由下式给出：

(35)

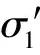
该例中岩体基本指标参数如表1所示。

表1 示例岩体破坏准则基本参数

Hoek-Brown准则等效强度参数的计算方法在文献[8]中已给出。示例中两准则等效过程的最小主应力区间下限值取σ3min=σtm，上限值σ3max按文献[8]中建议取值，示例中岩体为完整硐室围岩，埋深为20 m，得σ3max=224.5 MPa。等效参数计算结果如图2所示，可见，Sheorey准则在小主应力区间内的等效M-C强度参数为φS=20.4°，cS=33.0 MPa，而Hoek-Brown准则为φH=21.5°，cH=32.4 MPa，对应的强度参数相当接近。

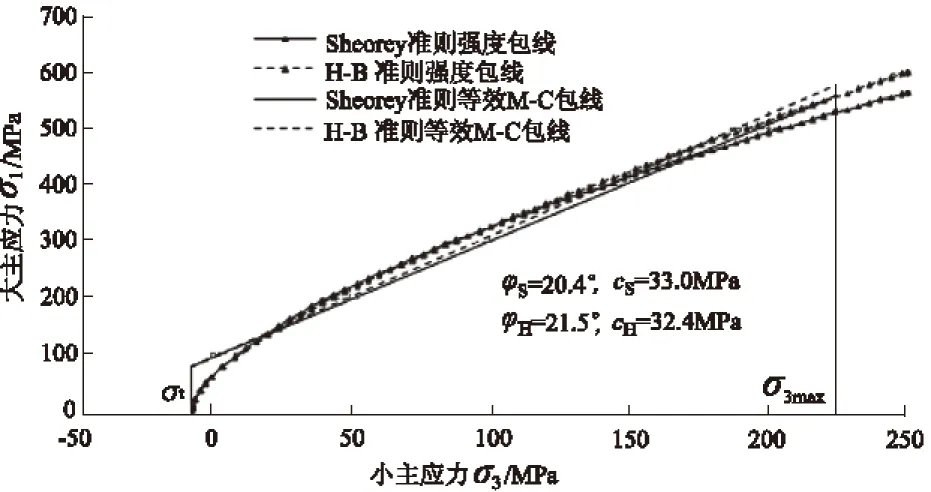
图2 Sheorey准则和Hoek-Brown准则等效M-C强度参数换算

5 结 论

本文从将非线性强度准则线性化的思想出发，根据一般的拟合原则，用线性M-C准则对Sheorey岩体强度准则进行了拟合，并推求出了等效M-C强度参数的通用表达式。在合理选取小主应力区间后，根据本文导出的结果能迅速求得相应的等效M-C强度参数，并方便地应用于计算分析。

从实例计算结果看来，在选定的小主应力区间内，Sheorey准则与Hoek-Brown准则的等效强度参数具有很好的一致性。且低围压下的Sheorey准则包线与Hoek-Brown包线几乎一致，而随着围压增大，两者偏差将增大。

参考文献：

[1] EDELBRO C.Evaluation of Rock Mass Strength Criteria[R].Sweden：Department of Civil and Mining Engineering, Division of Rock Mechanics，Lulea University of Technology, 2004.

[2] 李建林，陈兴周.岩体破坏准则及其参数研究[J].地下空间与工程学报, 2007, 3(5): 982-986.(LI Jian-lin, CHEN Xing-zhou.Study on Failure Criterion and Its Parameters for Rock Mass[J].Chinese Journal of Underground Space and Engineering, 2007, 3(5): 982-986.(in Chinese))

[3] 潘别桐.工程岩体强度的估算方法[J].地球科学：中国地质大学学报, 1985, 10(11): 63-67.(PAN Bie-tong.Estimation Method for Strength of Engineering Rock Mass[J].Earth Science: Journal of China University of Geosciences，1985, 10(11): 63-67.(in Chinese))

[4] 周小平, 钱七虎, 杨海清.深部岩体强度准则[J].岩石力学与工程学报, 2008, 27(1): 117-123.(ZHOU Xiao-ping，QIAN Qi-hu，YANG Hai-qing.Strength Criteria of Deep Rock Mass[J].Chinese Journal of Rock Mechanics and Engineering，2008, 27(1): 117-123.(in Chinese))

[5] 杨永兵.边坡岩石强度与岩体强度的工程变换[J].金属矿山，2004, (9): 10-12.(YANG Yong-bing.Engineering Transformation of Strength Between Rock and Rock Mass of Open-bit Slope[J].Metal Mine，2004, (9): 10-12.(in Chinese))

[6] 朱志明, 章广成, 朱娇燕, 等.基于广义 Hoek-Brown 准则的岩体等效强度[J].煤田地质与勘探, 2012, 40(4): 52-55.(ZHU Zhi-ming，ZHANG Guang-cheng，ZHU Jiao-yan，etal.Research on Equivalent Strength Rock Mass Based on Generalized Hoek-Brown Failure Criterion[J].Coal Geology and Exploration，2012, 40(4): 52-55.(in Chinese))

[7] HOEK E, BROWN E T.Empirical Strength Criterion for Rock Masses[J].Journal of Geotechnical Engineering Division，ASCE，1980,106(GT9):1013-1035.

[8] HOEK E, CARRANZA-TORRES C, CORKUM B.Hoek-Brown Failure Criterion(2002 ed)[C]// Proceedings of the 5th North American Rock Mechanics Symposium, Toronto, Ontario, Canada, July 7-10, 2002: 267-273.

[9] 吴黎辉.岩体经验强度准则研究[D].西安: 长安大学, 2004.(WU Li-hui.Study on Empirical Strength Criterion of Rock Mass[D].Xi’an: Chang’an University, 2004.(in Chinese))

[10] SOFIANOS A I, NOMIKOS P P.Equivalent Mohr-Coulomb and Generalized Hoek-Brown Strength Parameters for Supported Axisymmetric Tunnels in Plastic or Brittle Rock[J].International Journal of Rock Mechanics and Mining Sciences，2006，43(5): 683-704.

[11] FU W X, LIAO Y.Non-linear Shear Strength Reduction Technique in Slope Stability Calculation[J].Computer and Geotechnics，2011，37(3): 546-558.

[12] 杨 强, 陈英儒, 刘耀儒, 等.岩体等效强度参数确定的理论和方法[J].岩石力学与工程学报, 2008, 27(10): 1993-1999.(YANG Qiang，CHEN Ying-ru，LIU Yao-ru，etal.Theory and Method of Determining Equivalent Strength Parameters of Rock Mass[J].Chinese Journal of Rock Mechanics and Engineering，2008, 27(10): 1993-1999.(in Chinese))

[13] SHEOREY P R.Empirical Rock Failure Criteria[M].Rotterdam: Balkema,1997：176.

[14] SHEOREY P R, BISWAS A K, CHOUBEY V D.An Empirical Failure Criterion for Rocks and Jointed Rock Mass[J].Engineering Geology，1989，26(2)：141-159.