特高拱坝结构安全度再评价

王仁坤，张 冲，陈丽萍，钟贻辉

（1.中国电建集团 成都勘测设计研究院有限公司科技质量部，成都 610072；2.国家能源水电工程技术研发中心 高混凝土坝分中心，成都 610072）

1 研究背景

拱坝设计安全度并不代表拱坝实际安全度。水利行业规范［1］规定：容许压应力等于混凝土极限抗压强度除以安全系数，对于1级拱坝，基本荷载组合下，安全系数为4.0。水电行业规范［2］采用了分项系数法，将分项系数换算成单一安全系数后，要求1级拱坝抗压安全系数不低于4.4。

业界关于该安全系数的认识，存在不同的看法，其疑问在于：①是否偏高，国外一些发达国家，如美、欧、日、俄等，其结构设计表观安全系数［3］均小于我国；②是否偏低，目前全世界按照规范安全系数建设的拱坝，均存在普遍开裂现象。因此，如何认识拱坝的结构设计安全度，关系特高拱坝安全设计方法的严肃性，需要认真对待。本文尝试依托多拱梁法，分析探讨拱坝混凝土的实际强度以及拱坝结构的最大可能应力，从而论述拱坝结构的实际可能最小安全度，探讨当前规范安全系数取值的合理性。

目前，拱坝设计规范结构强度安全系数定义为

式中：fcu，k为大坝混凝土设计强度标准值，我国拱坝规范将其定义为90 d龄期、15 c m立方体试件、80%保证率的单轴抗压强度；S为多拱梁法计算出来的大坝主应力。

显然，拱坝混凝土实际强度并不等于实验室的设计强度标准值，由于尺寸、龄期、持久荷载、施工等各方面的影响，高拱坝混凝土实际强度要较设计强度标准值低。同时为安全起见，当前拱坝设计均要求拱坝工作在材料及结构弹性范围内，因此容许强度［Rc］的取值又进一步小于混凝土实际强度。

同样，拱坝结构的实际应力也并不等于由多拱梁法计算出来的应力，由于温度和水沙等荷载难以预测、地基和大坝混凝土材料参数估算误差、各类计算假定的影响、分级加载路径选择差异、分析方法本身不完备等，导致实际应力与计算应力差异较大。实际可能最大应力S′往往大于结构计算应力S。

因此，拱坝结构实际安全度K′可表述为

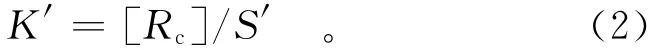
拱坝结构实际安全度K′＞1是确保拱坝长期稳定运行在拱坝材料弹性范围的必要选择。

2 拱坝混凝土材料容许使用强度

显然，容许强度［Rc］与设计强度标准值fcu，k并不一致，其可以表述为

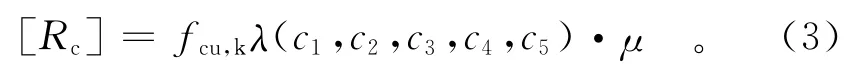
式中：λ（ci）为抗压强度修正函数，ci为抗压强度影响系数，i＝1，2，…，5，分别为尺寸效应、龄期效应、施工影响、多轴受力状态以及其他因素产生的影响系数；μ为材料的比例极限系数，其主要用于确保材料工作在弹性范围内。假定各修正因素相互独立，因此令

实际分析中应根据拱坝当时的运行状况，合理选择若干修正参数进行修正。

由于我国拱坝设计通常按照单轴强度进行设计，因此，本节暂不讨论多轴强度效应的影响，即取c4＝1.0，同时，其他因素影响效益取为c5＝0.95。

2.1 尺寸效应

通常工程现场难以直接测定大体积混凝土实际强度，因此需要依赖于室内小尺寸试件。小试件由于受试件尺寸、形状以及湿筛效应的影响，其测得的强度并不代表混凝土实际强度。因此，要获得混凝土的真实材料性能，必须对室内小尺寸试件的强度进行换算。研究［4］表明，当试件尺寸不小于3倍混凝土最大骨料尺寸的立方体或者圆柱体试件，可以近似代表大体积混凝土的强度特性，考虑到水工混凝土最大骨料尺寸通常在15 c m左右，因此本文采用45 c m圆柱体试件强度代表大坝混凝土实际强度。

2.1.1 形状

溪洛渡电站开展了大量混凝土抗压强度形状效应研究［5］，如表1所示。由表可见，试件形状对于试件试验强度存在重要影响，Ф450 mm×900 mm圆柱体试件强度通常低于450 mm立方体强度，其平均比值约为0.75。

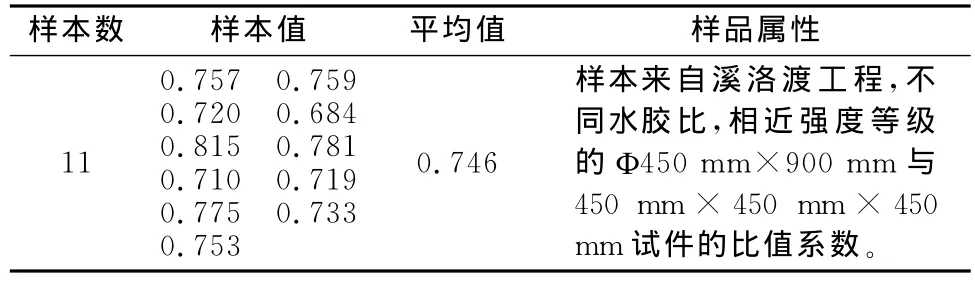
表1 形状效应试验统计表Table1 Statistics of speci mens with different shapes

《水工混凝土试验规程》［6］结合了七五、八五科技攻关［5］研究成果，提出形状系数值为0.775。《水工混凝土结构设计规范》［7］根据国内120组混凝土棱柱体与200 mm的立方体抗压强度的试验对比，两者的平均值比为0.76。其他研究表明各级尺寸的立方体试件与圆柱体（直径∶柱高＝1∶2）试件之间，均存在明显的形状效应，且比值系数均大致接近。

综合以上各成果分析，建议取形状系数为0.746。

2.1.2 尺寸

混凝土强度等多种性能都存在尺寸效应［8］。溪洛渡拱坝针对尺寸效应做了专门研究［5］，相关成果如表2、表3所示。从中可以得出3大结论：①混凝土尺寸效应明显，以90 d龄期混凝土受压试验为例，45 c m立方体与15 c m立方体试件强度比为0.83；②混凝土尺寸效应存在明显的龄期效应，28 d龄期以前，混凝土强度较低，尺寸效应亦不明显，90 d龄期以上，尺寸效应逐渐显性并趋于稳定。考虑到大坝受荷龄期均比较长，因此采用180 d龄期以上的尺寸效应系数是必要的；③混凝土的受拉尺寸效应和受压尺寸效应并不一致，以90 d龄期为例，受压尺寸效应为0.83，受拉效应为0.62。

表2 溪洛渡全级配混凝土试验配合比Table 2 Mix proportion of concrete in Xiluodu arch dam

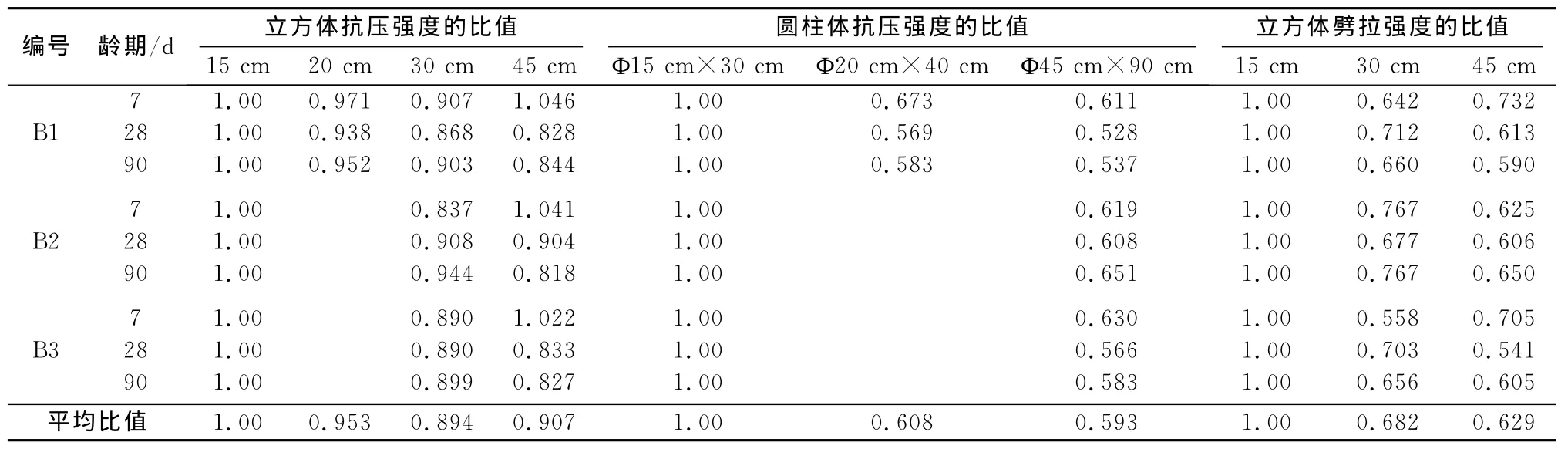
表3 溪洛渡水电站混凝土试件强度比值Table 3 Compressive strength ratios of concrete in Xiluodu arch dam

考虑到目前大量特高拱坝工程，均大量采用了180 d龄期85%保证率的混凝土，因此，本文收集了溪洛渡、锦屏一级、二滩、拉西瓦、小湾等300 m级特高拱坝大坝混凝土180 d龄期的相关尺寸效应资料，如表4所示。

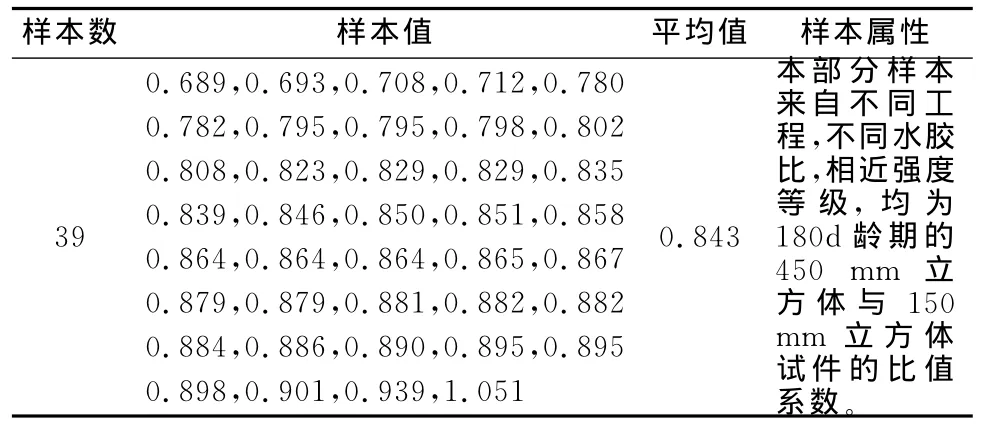
表4 尺寸效应系数试验结果统计Table 4 Statistics of size effect tests

收集到的样本数为39个，可视为有统计意义样本，其尺寸效应均值为0.843。

综上，考虑到特高拱坝的特殊性，本文推荐180 d龄期以上，受压尺寸效应系数取0.80。考虑形状效应、湿筛效应以及狭义上的尺寸效应后，整体的尺寸效应推荐值为c1＝0.61。

2.2 龄期效应

大坝混凝土设计采用设计龄期标准强度进行，一般采用90 d或180 d（美国采用360 d）作为设计龄期，但拱坝混凝土的运行至少也超过50 a，因此，相比于设计龄期，拱坝在运行期间其强度较设计龄期强度有较大幅度的增长，龄期效应不可忽略。

显然，大幅提升试件的试验龄期将急剧增加试验成本，因此利用现有资料，选取某合适的龄期强度代表大坝混凝土的长期龄期强度较为重要。

本文在收集溪洛渡等6座300 m级高拱坝工程试验数据的基础上，参考《水工混凝土结构设计规范》［7］、三峡大坝混凝土5a的试验成果［9］以 及George W.Washa等［10］给出了用几组混凝土50 a的试验成果，对大坝混凝土的强度发展系数进行统计（以180 d龄期强度为基准），如表5所示。

采用公式（5），以180 d龄期强度作为基准，对试验数据进行拟合。

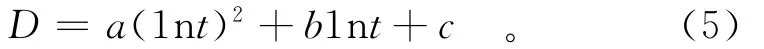
式中：D为强度发展系数；t为混凝土龄期（d）；a，b，c为拟合系数。

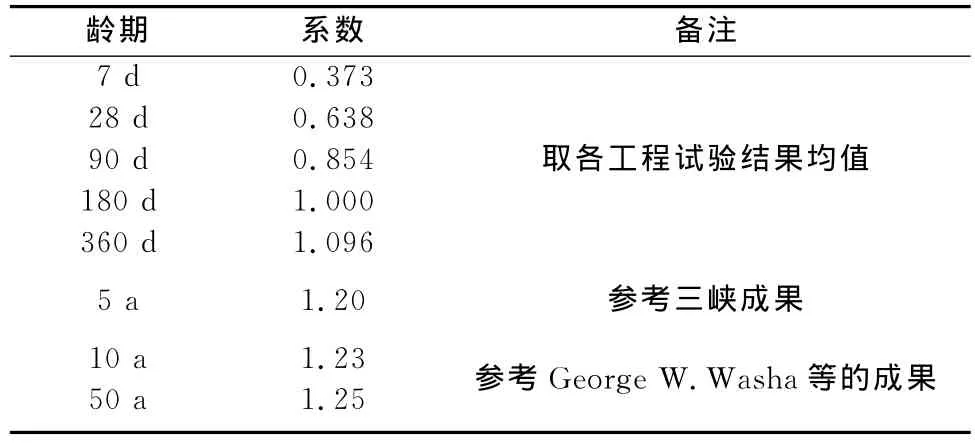
表5 大坝混凝土不同龄期抗压强度发展系数统计Table 5 Compressive strength coefficients of concrete with different ages

从偏安全角度，本文建议取结构最大应力出现时间作为参考龄期指标。目前国内多座特高拱坝工程，其结构分析最大应力点从浇筑到出现最大应力，通常在3 a左右。考虑一定富裕度，因此，选用拱坝混凝土2 a龄期作为最大应力出现的代表龄期是合适的。相应的抗压强度龄期增长系数为c2＝1.15。

2.3 施工影响

规范要求的室内小试件试验通常采用小型搅拌机、小型振动台等进行成型，然后标准养护并开展后续试验，从而获得试验强度；而现场通常采用大型拌和系统、运输系统（汽车、揽机等）、振捣设备（高频振捣器）进行混凝土生成、运输、振捣成型。这个过程必然对混凝土的强度产生影响，主要有：拌和系统影响因素、运输系统影响因素、浇筑过程影响因素、养护因素等4大因素。

显然，施工影响因素可以用最终的芯样强度与标准试件强度的比值来衡量。锦屏一级、溪洛渡等工程开展了大量的施工期影响因素研究，并钻取Φ290mm直径芯样进行抗压强度试验，成果如表6所示。

根据表6中数据估算出锦屏一级、溪洛渡等工程混凝土施工对混凝土强度的影响系数c3。

加权均值：c3＝0.96。

2.4 拱坝混凝土容许使用强度

表6 大坝混凝土芯样抗压强度Table 6 Compressive strength of concrete core samples from dam

混凝土是一种由水泥、沙子、骨料和水以及其他添加剂组成的既有物理反应又有化学反应的复合材料，在材料内部，骨料与砂浆之间、砂浆内部均存在大量原生的微裂隙。混凝土受压、应力逐渐增加最终破坏的过程，实际上就是微裂缝逐渐延伸、扩展并贯通的过程。

国内外曾有专家提出采用不连续点作为混凝土破坏的定义［5］。在不连续点上，混凝土的体积应变停止减小，泊松比开始急剧增加，混凝土的裂缝持续扩展，并开始出现不稳定。二滩试验结果表明单轴受压不连续点强度为极限强度的74%。在应力为极限强度的60%以内时，其应力-应变基本呈线性关系，混凝土内部即使存在微裂缝，也是稳定的。当应力超过60%的极限强度后，混凝土内部的微裂缝逐渐扩展。当应力超过74%极限强度后，裂缝严重扩展，逐渐进入塑化状态。随着应力的增加，裂缝互相连通，裂缝体系失稳而破坏。本文以二滩工程为例，暂时取不连续点系数为：μ＝0.74。

但显然，在不连续点范围内工作，能保证结构处于弹性范围内，当然会包含少量的塑性变形。鉴于上述讨论，为了获得混凝土相对真实的强度，同时保证混凝土能出于弹性工作状态，建议当混凝土受压时，采用表7的折减系数。

表7 拱坝混凝土实际容许强度折减系数Table 7 Reduction coefficients of concrete’s allowable strength of arch dam

上述分析表明，考虑以上影响因素后，拱坝混凝土实际强度约相当于试件强度的64%（考虑c1，c2，c3，c5）。但该强度尚未考虑混凝土的应力应变特性，大量混凝土试件试验揭示，混凝土试件受载小于单轴极限强度的50%时，基本可以确保混凝土工作在线弹性工作范围；当荷载继续增加，不超过试件强度的74%（统计意义上的不连续点）时，统计表明试件逐渐突破线弹性工作范围，出现少量的细观裂纹，但整体依然属于非线性弹性范畴。因此，要确保特高拱坝运行在弹性工作范围，其混凝土允许使用强度不宜大于试件强度的64%×50%＝32%；考虑到拱坝混凝土属于大体积混凝土，温度控制比较复杂，同时结构整体必须保证足够的刚度，混凝土强度标准不能无限提高，目前特高拱坝大量采用C18025至C18040。混凝土的容许使用强度不超过8～13 MPa。

需要注意的是，混凝土容许使用强度并不代表拱坝结构的容许应力，拱坝结构的容许应力应考虑应力成果的影响因素，考虑地质条件的复杂性以及抗震安全等要求，在允许使用强度的基础上进一步降低。目前二滩、溪洛渡等国内6座特高拱坝工程，容许应力标准均不超过8～10 MPa是较为合适的。

3 拱坝结构实际应力分析

如前文所述，拱坝实际可能最大应力S′往往大于结构的计算应力S，其可以表述为

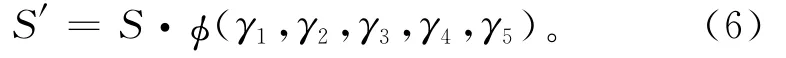
式中：φγi为应力修正函数，γi为相关修正系数，i＝1，2，…，5，分别为计算荷载修正、材料参数修正、计算方法修正、施工方法和加载路径修正、其他误差修正等；同样假定各修正因素相互独立，令

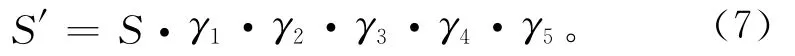
3.1 荷载变化的影响分析

作用在坝体上的荷载包括水压力、自重、温度作用、淤砂压力、波浪压力和地震作用等。由于设计是采用定值分析，上述各项作用均是确定的标准值，而实际上，这些作用都是随机过程，分析时必然存在取值的近似性，进而影响分析成果，其中尤其以水压力、温度等作用影响最大。但显然，由于拱坝是超静定结构，各荷载的作用效应之间不具备独立性，因此可采用包络的方法研究其最大可能的作用效应。监测显示，国内若干重大工程，正常运行时，存在水位突破正常蓄水位的情况，但频次普遍小于1%，超过幅度普遍小于50 c m，为安全起见，本文假定正常运行时，正常蓄水位会上下波动1 m，淤沙高程假定上浮5 m，其余参数上浮10%以及考虑对最大主压应力影响最大的温度荷载组合。以上述包络原则对溪洛渡、锦屏一级拱坝的分析成果如表8。计算显示，采用包络线方法分析各种作用不利因素组合下对坝体应力的影响幅度最大不超过5%。作用荷载不确定性修正系数主要来自水压、淤砂和温度荷载的不确定性。。综合考虑取作用荷载不确定性修正系数γ1＝1.05。

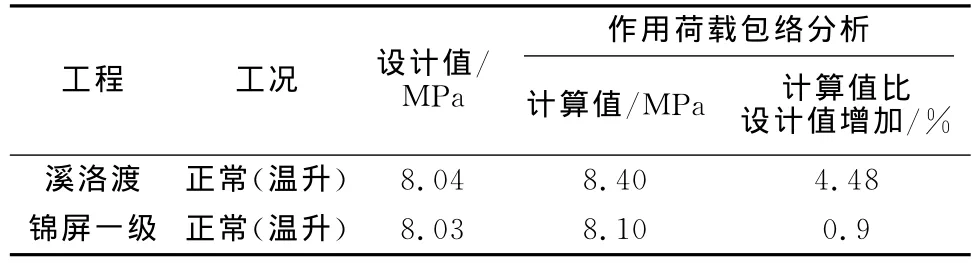
表8 坝面最大主压应力Table 8 Maxi mum principal compressive stress of dam surface

3.2 材料参数的影响分析

通常影响坝体应力的材料参数主要有：坝体及地基的变形模量、泊松比。

以溪洛渡等工程为例，考虑混凝土泊松比在设计取值±10%以内进行浮动取值，研究混凝土泊松比对坝体应力的影响见表9。

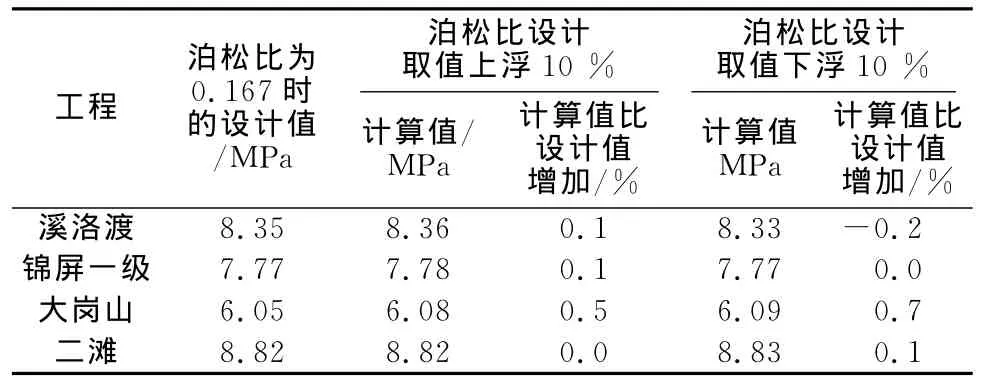
表9 基本荷载组合下泊松比对坝面最大主压应力的影响Table 9 I mpact of Poisson ratio on the maxi mu m principal compressive stress of dam under basic load combination

由表9可见，可能的最大控制压应力比设计工况控制性最大主压应力高出0.7%。因此混凝土泊松比变化的影响可忽略不计。虽然岩石的随机特性更强，泊松比的变化范围更为宽泛，但从宏观统计角度而言，目前我国所取的基岩泊松比是符合岩体特性的，对大坝应力的影响也不明显。因此本文不考虑材料泊松比对大坝应力的影响。

由于地基变形模量变化规律较为复杂，除了天然因素，施工过程中的地基置换、地层岩级变化、坝基开挖引起的岩体松弛、地基固结灌浆效果等也会影响地基变形参数计算取值。单纯的上下浮动敏感性分析难以穷尽最不利工况，其目的仅在于分析拱坝体形对地基条件可能发生变化的适应能力。实际最大应力可能会出现在单岸浮动，或者局部高程区段浮动中，因此难以采用包络方法对其进行研究。

二滩工程设计过程中，随着对建基面地质条件认识的不断深化，左右岸地基的综合变形模量不断进行了调整。记录显示，由于地基变模的取值变化，使二滩拱坝的计算最大主压应力大致比正常设计状况增加6%。

溪洛渡拱坝工程地质条件良好，未见断层发育，地基岩体中发育的不同规模的层间、层内错动带及基体裂隙控制了岩体结构，影响岩体的质量及力学特性。招标设计假定整体、一岸、或局部高程的变形模量浮动20%～30%。敏感性分析结果显示，当河床400.00 m高程以下地基变模下降20%时，最大主压应力变化最大，从正常设计时的8.35 MPa提高至8.83 MPa，提高5.7%。

小湾拱坝地基综合变形模量敏感对大坝应力影响不大。以设计变模、可能高值、可能低值、可能高值的1.1倍以及可能低值的0.9倍这5种条件进行分析，可能的最大控制应力为10.50 MPa，比设计工况控制性最大主应力10.37 MPa提高了1.25%。

锦屏一级拱坝地质条件复杂，建基岩体综合变形模量在10～19 MPa之间，岩体包含Ⅱ—Ⅴ1级岩体。假定左右岸地基变形模量不管是同时还是某一岸浮动15%，基础最大主压应力都将增加约2%；在极端情况下，仅仅将右岸局部Ⅱ级岩体的地基综合变形模量上浮15%时（相当于将Ⅱ级岩体提升至Ⅰ级岩体），加大了与邻近岩体综合变形模量的差距，最大主压应力将增加约6%。

大岗山拱坝分析结果显示，当右岸设计变模整体上浮20%时，最大主压应力变化最大，将从正常设计时的6.27 MPa提高至6.88 MPa，提高9.7%。

通过对上述5个特高拱坝的敏感性分析，基础边界约束条件不定性的影响，当地基变形模量整体浮动时，对坝体的影响较小，只有在局部地区地基变形模量变化很大时，加大了相邻控制拱圈高程地基变形模量的差距时，会导致应力恶化，通常情况下，对坝体的影响不超过10%。综合考虑取材料参数不确定性修正系数γ2＝1.10。

3.3 计算影响分析

多拱梁法根据拱梁杆件系统相同点变位一致原理，将拱坝视为由若干水平拱圈和竖直悬臂梁组成的空间结构，荷载由梁系和拱系分担，荷载分配由变位一致来确定，通过建立变位方程，一次求解外荷载在拱梁系统上的分配，从而分别计算出拱、梁杆件系统的内力、变位和应力。

在实际操作过程中，各家程序在算法实现上又存在若干不同的处理方式，如基础边界约束条件不定性、不同计算网格以及不同调整向数等等。在《混凝土拱坝设计规范》［1］修编时，对二滩等10个拱坝，按不同的拱、梁剖分网格数目进行了相对比较表明：高拱坝拱、梁剖分网格数目应不低于7拱13梁，当拱数达到9～10拱以后，控制压应力基本稳定，因此可不考虑该网格划分的影响。其余2大因素，规范并未限定具体的要求，各方法皆为可用。

“七五”国家科技攻关［5］采用浙江大学BEMS程序、中国水利水电科学研究院ADAS程序、河海大学ADAOP75程序以及成都勘测设计研究院有限公司ADSC-CK程序对基本荷载组合工况下的二滩拱坝招标体形进行了不同调整向数的多拱梁法坝体应力计算，见表10。考虑到拱坝通常设有横缝，且坝体边浇筑上升边封拱灌浆，因此竖向变位调整以及绕径向轴的角变位是没有意义的，计算时可以完全忽略。因此，以四向成果作为基准对成果进行整理。

由表10可见，不同软件之间的基础处理方式以及调整向数，计算压应力最大可能上浮约13.7%，综合确定不同计算方法对应力值的影响系数为：γ3＝1.14。

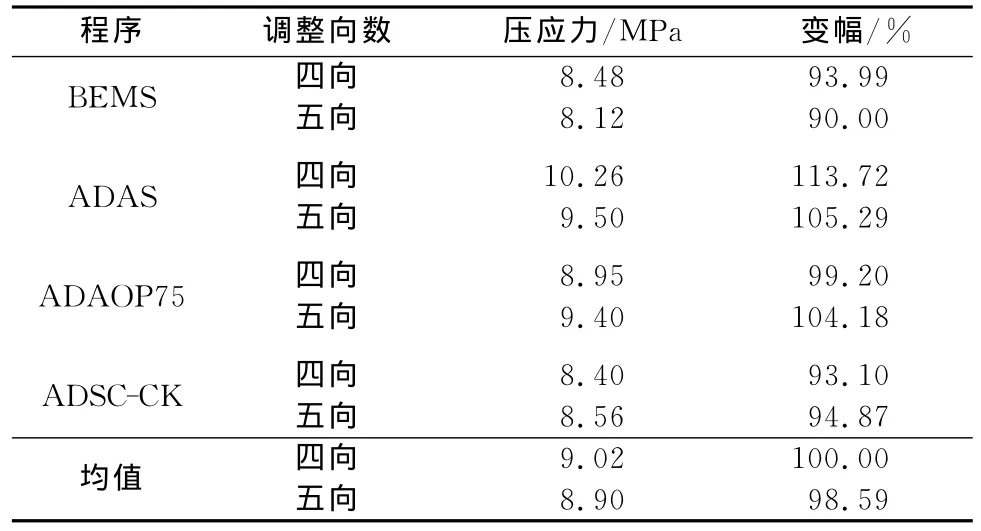
表10 各个计算程序控制压应力比较Table 10 Comparison of control compressive stresses of different calculation programs

3.4 分级封拱与加载路径的影响分析

由于施工过程不连续性以及接缝灌浆的影响，浇筑过程应力会积累到运行期大坝初始应力场中。因此不同施工过程对竣工后坝的整体应力有较大影响［11］。常规分析方法没有明确约定拱坝自重施加方式。通常将其分为整体自重和分缝自重。实际拱坝施工过程，通常是浇筑、接缝灌浆交替进行，封拱完成的区域，自重荷载在拱梁之间进行分配，未灌浆区域，自重有各自独立的梁承担，研究表明，真实模拟施工过程的拱坝自重应力状态介于整体自重与分缝自重之间。

溪洛渡计算显示，将施工及蓄水过程根据实际情况概化为13个阶段后，在组合温降条件下，下游坝面最大主压应力为8.69 MPa，比按正常设计情况的最大主压应力8.43 MPa增加了3.1%；在组合温升条件下，下游坝面最大主压应力为9.01 MPa，比按正常设计情况的最大主压应力8.75 MPa增加了3%；

同样，二滩概化为13个阶段后，在组合温降条件下，考虑施工工艺影响后的坝体最大主压应力为9.42 MPa，比按正常设计情况的最大主压应力8.82 MPa增加了6.8%。

锦屏一级拱坝将施工及蓄水过程根据实际情况概化为8个阶段后，组合温降工况，下游坝面最大主压应力，从正常设计7.77 MPa，增加到8.0 MPa，约增加了3%。组合温升工况，下游坝面最大主压应力，从正常设计的7.93 MPa，增加到8.15 MPa，增加了2.8%；

从上述3个工程的模拟分析，施工程序及蓄水过程对坝体应力重分布的影响不超过7%，随坝体的高度、拱坝形体（跨高比、厚高比）的不同、河谷形状的差异、以及施工程序和蓄水过程的不同，对坝体应力重分布的影响有很大的差异。从已建和在建工程模拟的结果分析，可暂定该项影响的修正系数为γ4＝1.07。

3.5 其它因素影响

除多拱梁法计算模型固有缺陷影响外，如U型、V型河谷形态对坝体应力的影响；坝内设置的孔口、闸墩等附属设施亦无法考虑，这些综合因素影响，可参照前述主要因素修正给出一定富裕值，定为γ5＝1.05。

综上，根据多拱梁法的计算，实际可能最大应力将在标准计算应力的基础上大幅提升，其提升幅度为

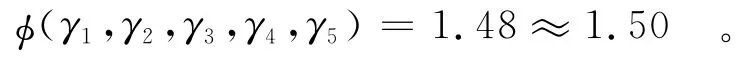
4 拱坝实际安全度

根据式（1）、式（2）、式（4）、式（7），大坝实际安全系数K′应为

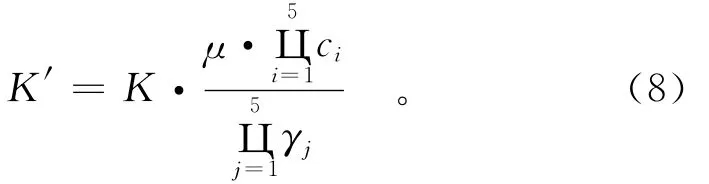
利用式（8）可以大致估算基于规范方法的拱坝实际安全度，当然由于各影响因素取值并不完全符合实际，甚至存在部分应该考虑但没有被考虑到的修正因素，因此最终的实际安全度并不一定体现大坝的真实安全度，但可以肯定的是，基于这种方法的安全系数较规范安全系数更接近于拱坝的安全状况。

根据式（8）的修正方法，对《拱坝设计规范》的表观安全系数进行修正，其对应的实际安全系数如表11所示。由于本文分析时仅针对特高拱坝进行了分析，未涉及中小工程，故不对中小工程的实际安全系数进行讨论。

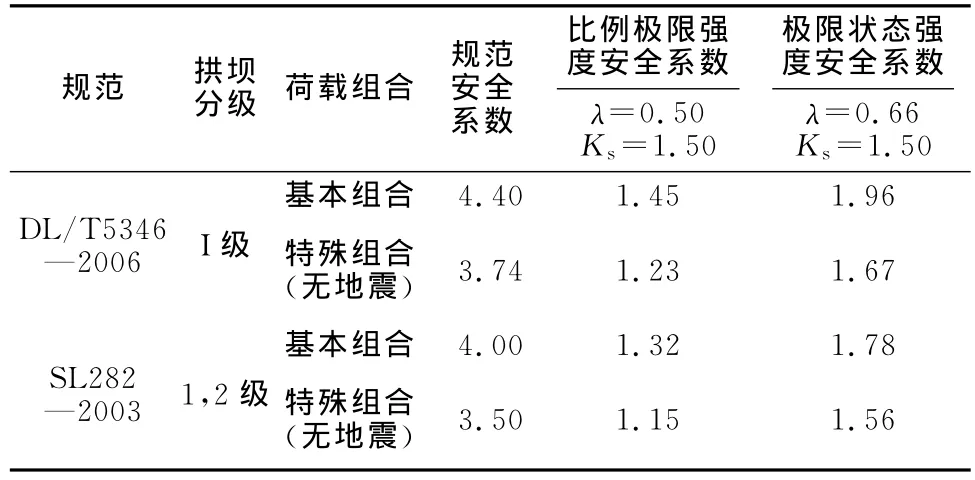
表11 拱坝规范坝体强度实际安全系数Table 11 Corrected actual safety f actors corresponding to safety f actors in Specification

实际安全系数的分析表明，按照规范设计方法设计的拱坝，尤其是中高拱坝，考虑各种不利因素之后，可以确保拱坝的实际最小安全度大于1.0，即可以确保拱坝在基本组合以及特殊组合（无地震）情况下工作在线弹性范围内。同时，数据也显示，拱坝实际安全度并没有过高的安全裕度，当前规范的安全控制标准是合理的。

5 结 论

（1）分析表明高拱坝混凝土由于存在尺寸效应、龄期效应、长期持荷强度影响、施工影响等，其实际强度与混凝土标准试件强度存在巨大的差异。已有的统计数据表明，考虑以上影响因素，同时要求拱坝应力不超过不连续点强度以保证拱坝工作在弹性范围内，拱坝混凝土的容许强度约相当于混凝土标准试件强度的48%。目前二滩、溪洛渡等国内6座特高拱坝工程，允许应力标准均不超过8～10 MPa是较为合适的。

（2）我国《拱坝设计规范》规定的拱坝安全控制标准并不代表拱坝实际安全度，考虑混凝土强度以及计算应力修正后，我国Ⅰ级拱坝实际安全度接近或略超过1.0，这充分说明规范安全控制标准是确保拱坝长期处于弹性工作状态的客观要求，当前规范的安全系数取值是相对合理的。

［1］DL／T 5346—2006，混凝土拱坝设计规范［S］.北京：中国电力出版社，2007.（DL／T 5346—2006，Design Specification for Concrete Arch Dam［S］.Beijing：China Electric Power Press，2007.（in Chinese））

［2］SL282—2003，混凝土拱坝设计规范［S］.北京：中国水利水电出版社，2003.（SL282—2003，Design Specification for Concrete Arch Dam［S］.Beijing：China Water Power Press，2003.（in Chinese））

［3］董福品，朱伯芳，沈之良，等.国内外高拱坝应力分析概况［J］.中国水利水电科学研究院学报，2003，1（4）：292-299.（DONG Fu-pin，ZHU Bo-fang，SHEN Zhi-liang，et al.A Survey of High Arch Dam Stresses in the World［J］.Journal of China Institute of Water Resources and Hydropower Research，2003，1（4）：292-299.（in Chinese））

［4］能源部、水利部成都勘测设计研究院.高混凝土坝设计计算方法与设计准则［R］.北京：能源部、水利部成都勘测设计研究院，1990.（Chengdu Engineering Corporation.Calculation Method and Design Rules for High Concrete Dam［R］.Chengdu：Chengdu Engineering Corporation，1990.（in Chinese））

［5］杨忠义.全级配混凝土强度的尺寸效应研究［J］.水电站设计，2008，（9）：11-14.（YANG Zhong-yi.St udy of Effect of Complete Grading Concrete Strength［J］.Design of Hydroelectric Power Station，2008，（9）：11-14.（in Chinese））

［6］DL／T 5150—2001，水工混凝土试验规程［S］.北京：中国电力出版社，2002.（DL／T 5150—2001，Specification f or Tests on Hydraulic Concrete［S］.Beijing：China Electric Power Press，2002.（in Chinese））

［7］DL／T 5057—2009，水工混凝土结构设计规范［S］.北京：中国电力出版社，2009.（DL／T 5057—2009，Design Standard for Hydraulic Concrete Structure［S］.Beijing：China Electric Power Press，2009.（in Chinese））

［8］朱伯芳，高季章，陈祖煜，等.拱坝设计与研究［M］.北京：中国水利水电出版社，2002.（ZHU Bo-fang，GAO Ji-zhang，CHEN Zu-yu，et al.Design and Research for Concrete Arch Dams［M］.Beijing：China Water Power Press，2002.（in Chinese））

［9］李文伟，郑 丹，陈文耀，等，三峡工程大坝混凝土长龄期性能试验研究［J］.水利发电，2009，35（12）：76-81.（LI Wen-wei，ZHENG Dan，CHEN Wen-yao，et al.Long Age Perfor mance Test of Dam Concrete of Three Gorges Project［J］.Water Power，2009，35（12）：76-81.（in Chinese））

［10］WASHA G W，SAEMANN J C，CRA MER S M.Fifty-year Properties of Concrete Made in 1937［J］.ACI Materials Jour nal，1989，86（4）：367-371.

［11］张国新，刘 毅，朱伯芳，等.高拱坝真实工作性态仿真的理论与方法［J］.水力发电学报，2012，31（4）：167-174.（ZHANG Guo-xin，LIU Yi，ZHU Bo-fang，et al.Theory and Method on Simulation of Actual Working Perfor mance of High Arch Dams［J］.Journal of Hydroelectric Engineering，2012，31（4）：167-174.（in Chinese））