基于改进粒子群算法的小波神经网络在变压器故障诊断中的应用

程声烽，程小华，杨 露



基于改进粒子群算法的小波神经网络在变压器故障诊断中的应用

程声烽，程小华，杨 露

(华南理工大学电力学院，广东 广州 510640)

针对变压器故障征兆和故障类型的非线性特性，结合油中气体分析法，设计了一种改进粒子群算法的小波神经网络故障诊断模型。模型采用3层小波神经网络，并用一种改进粒子群算法对其进行训练。该算法在标准粒子群算法的基础上，通过引入遗传算法中的变异算子、惯性权重因子和高斯加权的全局极值，加快了小波神经网络训练速度，提高了其训练的精度。仿真实验证明这种改进粒子群算法的小波神经网络可以有效地运用到变压器故障诊断中，为变压器故障诊断提供了一条新途径。

改进粒子群算法；小波神经网络；变压器；故障诊断

0 引言

电力变压器的安全可靠运行对于电力系统、国民经济起着非常重要的作用。能否快速准确地诊断和预测出变压器已有故障或潜伏性故障对电力系统稳定运行具有重要的现实意义。传统的变压器故障诊断方法中，以油中气体分析法（DGA）应用最为广泛，其主要通过油中溶解气体与变压器故障类型之间的对应关系，在已知气体组分的情况下对故障类型进行诊断，IEC三比值法和改良电协研法就由此而来，但其编码范围的边界及编码类型过于绝对，影响故障诊断的精度，因此寻求高精度诊断方法迫在眉睫。随着人工智能和计算机技术的发展，各种智能技术为变压器故障诊断提供了一个新思路，其中小波神经网络（Wavelet Neural Network，WNN）便是其中之一。传统的WNN以BP算法训练网络，而BP算法易出现收敛早熟、陷入局部极小值等情况，影响了网络训练的精度。为此，国内外专家学者提出各种改进算法来改善网络训练的精度，文献[10]将遗传算法应用于小波神经网络，构造了一个小波神经网络分类器，并成功应用于变压器故障诊断，但遗传算法编码和解码操作相对比较复杂；针对上述不足，文献[11]用改进粒子群算法取代遗传算法，利用粒子群算法的全局搜索能力优化小波神经网络，在变压器故障诊断中取代较好的效果；除此之外，文献[12]提出的加动量批处理小波神经网络算法，也极大地提高了变压器故障诊断效率，实用性较好。

本文在变压器故障诊断智能方法的基础上，首先构造了3层小波神经网络模型，然后通过在标准粒子群算法中加入变异算子、惯性权重因子和高斯加权的全局极值，构成一种改进的粒子群优化算法，并将其运用于小波神经网络参数优化，通过变压器故障诊断结果表明这种改进的粒子群算法比相同条件下的BP算法和标准粒子群算法具有更好的收敛性。

1 小波神经网络构建

小波神经网络是一种基于小波变换理论而构造的前馈神经网络，其充分利用了小波变换的局部化性质和神经网络的大规模数据并行处理、自学习能力，因而具有较强的逼近能力和较快的收敛速度，其主要可分为松散型和紧密型两种类型。本文采用紧密型结构来构造小波神经网络，构造出来的3层小波神经网络如图1所示。

图1三层小波神经网络结构

通过前向计算得到隐含层第个小波元的输入为

，（1）

通过小波基伸缩平移系作用，隐含层第个小波元的输出为

则网络输出层第个节点输出为

网络输出误差能量函数为

由此可知，在确定输入节点、隐层节点和输出节点后，构造一个合适的小波神经网络的关键在于确定网络中的各个参数{，，，}，而这些参数的选取是否恰当，依赖于小波神经网络训练算法的优化，因此找到一种合适的小波神经网络训练算法就显得尤为重要。

2 改进粒子群算法优化小波神经网络

传统小波神经网络多以BP算法进行网络训练，但BP算法存在收敛速度慢、易陷入局部极小值等缺点，难以满足网络高精度训练的要求。本文提出一种改进粒子群算法，即在标准粒子群算法的基础上加入遗传算法中的变异算子、惯性权重因子和高斯加权的全局极值，并将其运用于优化小波神经网络各个参数。

标准粒子群算法的思想为：先初始化一群随机粒子，然后根据对个体和群体的飞行经验的综合分析来动态调整粒子群的速度，在解空间中进行搜索，通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己，一个是个体极值，即粒子自身目前所找到的最优解；另一个是全局极值，即整个种群目前找到的最优解。假设在一个维的目标搜索空间中，有个粒子组成一个群体。其中用向量表示第个粒子的位置，表示其对应的速度。当第个粒子被迭代到到目前为止最好的位置（即具有最佳适应度）时，此时该粒子被称为个体最好粒子，记为pbest，而当全部粒子迭代到截止当前为止最好位置时被称为全局最好粒子，记为。各粒子可根据以下公式来更新自己的速度和位置。

（5）

对上述标准粒子群算法进行三个方面的修改，构成本文的改进粒子群算法，具体表现在：

①为了避免粒子群算法搜索精度低、后期迭代效率不高的现象，借鉴遗传算法中的变异思想，在粒子群算法中加入变异算子，即粒子每次更新之后都以一定的概率重新初始化粒子，变异操作拓宽了迭代中不断缩小的种群搜索空间，使粒子能够跳出先前搜索到的最优位置，保持了种群的多样性。其相应的伪代码如下所示：

if 随机数概率大于0.9

则随机初始化种群

else 保持种群数值大小不变

③为解决迭代后期全局极值不易向最优解方向收敛的问题，引入高斯加权的全局极值。首先把所有粒子的适应度函数的平均值作为高斯加权的均值，其方差作为高斯加权的方差，即

再将当前粒子群的最小适应度值min作为高斯加权的中心，即可得到高斯加权的全局因子为

最后将所有粒子的个体极值pbest和上述高斯加权的全局因子进行加权平均，并将此值作为所有粒子的全局极值，即

通过高斯函数加权，在算法迭代后期，越靠近最优解的个体极值其权重越大，它们的乘积有利于全局极值向最优解方向收敛。

改进粒子群算法训练图1所示的三层小波神经网络步骤如下。

步骤1：初始化粒子群。确定粒子的维数（即网络中的各个参数{，，，}，初始化个粒子的位置、速度；设定学习因子、惯性权重的最大及最小值，最大迭代次数及目标误差值，并置此时的迭代次数为1。

步骤2：计算目标适应度值。对于每个粒子，利用小波神经网络的前向计算公式计算网络的实际输出，再利用式（4）计算其适应度值，排序取出最小的适应度值min。

步骤3：评价每一个粒子。个体极值更新：如果粒子适应度优于当前个体极值pbest，则将pbest设置为新位置，否则pbest不变；全局极值更新：将由式（10）计算出的高斯加权的全局极值确定为粒子群的全局极值。

步骤4：粒子位置和速度更新。利用式（5）更新每一个粒子的速度和位置，并以一定概率重新初始化粒子。其中速度的更新引入了由式（6）计算的惯性权重因子。

步骤5：检验是否符合结束条件。若当前的迭代次数达到了预先设定的最大次数（或达到最小误差要求），则停止迭代，输出最优解，否则转到步骤2。

3 小波神经网络的变压器故障诊断

3.1 输入量的确定

将上述改进粒子群算法优化的小波神经网络应用于变压器故障诊断中，在DGA的基础上，选择H、CH、CH、CH、CH及总烃（CH+CH+ CH+CH）的体积分数作为小波神经网络的输入变量，故输入节点的个数为6。为了充分采集数据的有效信息，首先对原始输入值进行粗大误差处理，去除明显影响网络收敛精度的输入量，再求出剩下输入数据相对于其注意值的隶属度，最后将此隶属度作为小波神经网络的输入，即

（11）

3.2 输出量的确定

选择低温过热O（<300℃）、中温过热O（300℃<<700℃）、高温过热O（>700℃）、局部放电或受潮O、低能放电O、高能放电O这6种典型单一故障类型作为小波神经网络的输出变量；实际故障时的输出有可能是单一故障的复合形式，故也选择高能放电兼高温过热OO、低能放电兼低温过热OO和高温过热兼中温过热OO这3种典型复合故障。输出节点的个数也为6，输出故障包含了所有单一故障类型和多故障类型。

3.3 隐层节点数的确定

网络的隐层节点个数有文献指出根据经验公式而来，即对6输入6输出小波神经网络而言，隐层节点数在12左右最佳。本文通过改变隐层节点个数来对比网络收敛性能，从而确定最为合适的隐层节点个数。选取相关参考文献公布的84组故障类型数据（其中55组单一故障类型数据、29组多故障类型数据）进行网络训练，10组故障数据（其中6组单一故障类型数据、4组多故障类型数据）进行网络测试，训练次数设置为700次，对比不同隐层节点个数情况下网络的均方误差（Mean Square Error，MSE），如表1所示。从中可以看出当隐层节点数为12时，训练样本和测试样本的MSE最小，故本文的小波神经网络的隐层节点数选为12。

3.4 变压器故障诊断结果及分析

在确定小波神经网络输入、输出及隐层节点之后，输入同样的变压器故障训练样本，且网络最大训练次数设置都设为1 500次，最小误差都设置为10，分别用BP算法优化的小波神经网络(BP-WNN)、标准粒子群算法优化的小波神经网络(PSO-WNN)和本文提出的改进粒子群算法优化的小波神经网络(改进PSO-WNN)对其进行训练，取最好的一次训

表1不同网络结构下的小波神经网络MSE比较

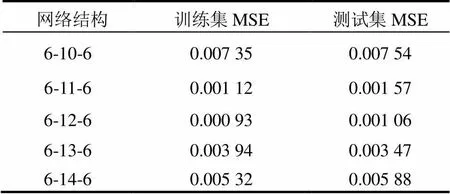
Table 1 Mean square error comparison of WNN under different network structures

练结果，由Matlab编程可得训练误差曲线如图2所示。

图2三种小波神经网络误差曲线比较

由图2可知，BP-WNN、PSO-WNN及改进PSO-WNN在变压器故障诊断中的平均误差、收敛时间及收敛精度等方面有显著差异。BP-WNN经过1455次达到预设精度，收敛时间长，主要原因为BP-WNN仅仅具有复杂的非线性映射能力，没有反馈，易陷入局部极小值，故不能较好地满足变压器故障诊断实时性的要求；PSO-WNN经过1119次达到预设精度，在迭代前期收敛速度快，迭代后期速度变慢，主要原因为在迭代后期粒子向自身历史最佳位置和群体历史最佳位置聚集，形成粒子种群的快速趋同效应，陷入了“停滞现象”，故也不能较好满足变压器故障诊断的要求；改进的PSO-WNN经过738次达到预设精度，收敛速度较前两者快，能够较好地满足故障诊断的要求。

训练完成之后，将训练好的小波神经网络用于变压器故障预测，由预测样本可以得到预测结果，然后再跟实际故障类型进行对比，以此评判故障预测的精度。为了检测改进PSO-WNN的诊断能力，将BP-WNN、PSO-WNN分别应用于变压器故障测试样本集，对单一故障和复合故障进行诊断，对各种算法在小波神经网络中诊断结果进行比较，部分比较结果如表2所示。

表2三种算法结果比较

Table 2 Comparison of the results of the three algorithms

由表2可以看出，无论是单一故障（测试样本1、2、3）还是复合故障（测试样本4、5），改进PSO-WNN诊断误差比BP-WNN和PSO-WNN诊断误差都要低，即利用改进的粒子群算法优化小波神经网络的各个参数，可以显著地提高网络的效率和收敛能力，泛化能力较BP-WNN和PSO-WNN强。

4 结论

本文针对变压器故障诊断实时性和高精度的要求，提出了利用小波神经网络对故障进行诊断，针对传统小波神经网络算法收敛速度慢、易陷入局部极小值等缺点，提出了一种改进的粒子群优化算法，并将其运用于小波神经网络参数优化中。仿真结果表明，本文所采用的改进粒子群算法比传统BP算法及PSO算法的训练精度高、收敛速度快，提高了变压器诊断的准确性。但是网络测试表明，复合故障的诊断误差比单一故障的诊断误差要大，因此，如何减小复合故障的诊断误差，提高对其诊断的精度是下步研究的重点。

[1] 刘丽, 唐杰, 刘卓. 基于改进微分进化优化神经网络的电力变压器故障诊断[J]. 电力系统保护与控制, 2010, 38(20): 106-109.

LIU Li, TANG Jie, LIU Zhuo. Power failure diagnosis improved differential evolution based on neural network optimized transformer[J]. Power System Protection and Control, 2010, 38(20): 106-109.

[2] 董其国. 电力变压器故障与诊断[M]. 北京: 中国电力出版社, 2001.

DONG Qi-guo. Power transformer fault and diagnosis[M]. Beijing: China Electric Power Press, 2001.

[3] 许慧君, 王宗耀, 苏浩益. 基于 DGA 的反馈云熵模型电力变压器故障诊断方法研究[J]. 电力系统保护与控制, 2013, 41(23): 115-119.

XU Hui-jun, WANG Zong-yao, SU Hao-yi. Research cloud feedback power transformer fault diagnosis based on entropy model approach DGA[J]. Power System Protection and Control, 2013, 41(23): 115-119.

[4] 龚瑞昆, 马亮, 赵延军, 等. 基于量子神经网络信息融合的变压器故障诊断[J]. 电力系统保护与控制, 2011, 39(23): 79-84.

GONG Rui-kun, MA Liang, ZHAO Yan-jun, et al. Quantum transformer fault diagnosis based on neural network information fusion[J]. Power System Protection and Control, 2011, 39(23): 79-84.

[5] 龙伯华, 谭阳红, 许慧, 等. 基于量子神经网络的电力电子电路故障诊断[J]. 电工技术学报, 2009, 24(10): 170-175.

LONG Bo-hua, TAN Yang-hong, XU Hui, et al. Fault diagnosis of power electronic circuits based on quantum neural network[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 170-175.

[6] 李鑫滨, 朱庆军. 一种改进粒子群优化算法在多目标无功优化中的应用[J]. 电工技术学报, 2010, 25(7): 137-143.

LI Xin-bin, ZHU Qing-jun. An improved particle swarm optimization algorithm for multi-objective optimization of reactive power[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 137-143.

[7] 尹金良, 朱永利, 俞国勤, 等. 基于高斯过程分类器的变压器故障诊断 [J]. 电工技术学报, 2013, 28(1): 158-164.

YIN Jin-liang, ZHU Yong-li, YU Guo-qin, et al. Transformer fault diagnosis based on Gaussian process classifier[J]. Transactions of China Electrotechnical Society, 2013, 28(1): 158-164.

[8] 庄哲民, 殷国华, 李芬兰, 等. 基于小波神经网络的风力发电机故障诊断[J]. 电工技术学报, 2009, 24(4): 224-228.

ZHUANG Zhe-min, YIN Guo-hua, LI Fen-lan, et al. Wind turbine fault diagnosis based on wavelet neural network[J]. Transactions of China Electrotechnical Society, 2009, 24(4): 224-228.

[9] 崔东军, 刘念, 刘秀兰. 基于加权小波神经网络的油浸式电力变压器故障检测[J]. 电力系统保护与控制, 2010, 38(18): 19-23.

CUI Dong-jun, LIU Nian, LIU Xiu-lan. Oil-immersed power transformer fault detection based on weighted WNN[J]. Power System Protection and Control, 2010, 38(18): 19-23.

[10] 马文静. 基于遗传算法小波神经网络的电力变压器故障诊断[J]. 自动化技术与应用, 2008, 27(12): 17-30.

MA Wen-jing. Power transformer fault diagnosis of genetic algorithm based on wavelet neural network[J]. Techniques of Automation and Applications, 2008, 27(12): 17-30.

[11] 贾嵘, 李宏斌, 康会西, 等. 改进粒子群优化神经网络在变压器故障诊断中的应用[J]. 高压电器, 2010, 46(5): 14-17.

JIA Rong, LI Hong-bin, KANG Hui-xi, et al. Improved particle swarm optimization neural network in fault diagnosis of transformer[J]. High Voltage Apparatus, 2010, 46(5): 14-17.

[12] UARDADO J L, NAREDO J L, MORENO P, et al. a comparative study of neural network efficiency in power transformers diagnosis using dissolved gas analysis[J]. IEEE Trans on Power Delivery, 2001, 16(4): 643-647.

[13] DELYON B, JUDITSKY A, BENVENISTE A. Accuracy analysis for wavelet approximations[J]. IEEE Trans on NN, 1995, 6(2): 332-348.

[14] VAN OOYEN A, NIENHUIS B. Improving the convergence of back-propagation algorithm[J]. Neural Networks, 1992, 5: 465-471.

[15] LIU Jin-yang, GUO M Z, DENG C. GeesePSO: an efficient improvement to particle swarm optimization[J]. Computer Science, 2006, 33(11): 166-168.

[16] SUN Q, MI C, LAI L L, et al. A fuzzy dissolved gas analysis method for the diagnosis of multiple incipient faults in a transformer[J]. IEEE Trans on Power Systems, 2000, 15(2): 593-598.

[17] 方健, 彭辉, 李自品, 等. 改进小波网络在油浸式变压器故障诊断中的应用[J]. 高压电器, 2011, 47(11): 115-120.

FANG Jian, PENG Hui, LI Zi-pin, et al. Improved wavelet network in oil-immersed transformer fault diagnosis[j]. High Voltage Apparatus, 2011, 47(11): 115-120.

[18] 李建坡. 基于油中溶解气体分析的电力变压器故障诊断技术的研究[D]. 吉林: 吉林大学, 2008.

LI Jian-po. Study on power transformer fault diagnosis technology based on dissolved gases analysis[D]. Jilin: Jilin University, 2008.

[19] 王耀龙. 基于油中溶解气体分析的电力变压器故障诊断[D]. 桂林: 广西大学, 2005.

WANG Yao-long. Power transformer fault diagnosis based on dissolved gas analysis[D]. Guilin: Guangxi University, 2005.

[20] 李俭. 大型电力变压器以油中溶解气体为特征量的内部故障诊断模型研究[D]. 重庆: 重庆大学, 2001.

LI Jian. Study on the models of fault diagnosis about power transformer based on dissolved gases analysis[D]. Chongqing: Chongqing University, 2001.

Application of wavelet neural network with improved particle swarm optimization algorithm in power transformer fault diagnosis

CHENG Sheng-feng, CHENG Xiao-hua, YANG Lu

(School of Electric Power, South China University of Technology, Guangzhou 510640, China)

In view of non-linear characteristics between fault symptoms and fault types of transformers, a wavelet neural network fault diagnosis model based on improved particle swarm algorithm is designed with the data of dissolved gas analysis. The model, constructed by three-layer wavelet neural networks, is trained by an improved particle swarm algorithm. By introducing the mutation operator of genetic algorithm, inertia weight factor and Gaussian-weighted global extremes on the basis of the standard particle swarm algorithm, it can accelerate the training speed of wavelet neural network and improve the accuracy of training. The simulation experiments show that this improved particle swarm algorithm wavelet neural network can be effectively applied to transformer fault diagnosis and provides a new way for transformer fault diagnosis.

improved particle swarm algorithm; wavelet neural network; transformer; fault diagnosis

TM41

A

1674-3415(2014)19-0037-06

2013-12-20；

2014-03-19

程声烽（1990-），男，硕士研究生，主要研究方向为电机控制；E-mail: 1074375156@qq.com

程小华（1963-），男，博士，教授，主要从事电机基本理论特别是交流电机绕组理论、电机设计、电机控制以及新型电机的研究；

杨 露（1990-），女，硕士研究生，主要研究方向为蓄电池中的电力电子控制技术、微网优化。