优化和声算法在含DG配电网故障定位中的应用

高云龙，周羽生，彭 湃，刘让姣，安正洲



优化和声算法在含DG配电网故障定位中的应用

高云龙，周羽生，彭 湃，刘让姣，安正洲

(长沙理工大学电气与信息工程学院，湖南 长沙 410114)

为了提高含DG配电网故障定位的速度和容错性，提出利用高度并行、鲁棒性强的遗传算法来优化基本和声算法对初始化和声记忆库的过度依赖性，改进了和声算法中新解的产生方式。针对含DG配电网的结构特点引入“树”的区域划分方法以降低求解维度，根据故障定位最小集理论优化评价函数以提高容错性。分别利用优化前、后的和声算法对相同配电网模型进行寻优运算和分析比较，结果表明优化的和声搜索算法能够有效地提高算法收敛速度和故障定位精度，在信息缺失、畸变等情况下具有良好的容错性。

分布式电源；配电网；故障定位；优化和声算法；评价函数

0 引言

故障定位一直是配电网技术领域的重要课题。近年来，国内外学者提出了许多智能算法，如遗传算法，粒子群算法，免疫算法等，这些算法鲁棒性强、容错性好，但是其定位的精度和运算速度有待进一步提高。

和声搜索(HS)算法是Geem等人通过类比音乐演奏和最优化问题的相似性而提出的一种现代启发式智能化优化算法。该算法较其他智能算法具有更好的优化性能，但该算法的和声记忆库是随机产生的，具有不确定性，且对记忆库的初始化具有很强的依赖性。本文在文献[12]的研究基础上，利用具有高度并行、鲁棒性强等优点的遗传算法（GA）产生和声库的初始解，同时改进和声库中新解的产生方式，克服了对初始和声记忆库依赖性强和参数随机选择不确定性的弊端。将优化后的和声算法（GAHS）与基本的HS分别对相同的含DG配电网模型进行算例仿真分析比较，结果表明优化后和声算法能够有效地提高故障定位的容错能力和算法收敛速度。

1 和声算法优化方法

1.1基本和声算法

和声搜索（HS）算法主要受启于音乐演奏搜寻完美和声的过程。每一种乐器类比于优化问题的决策变量，乐师通过反复调整每种乐器的音调而使音乐达到美妙动听的过程类似于不断调节变量使优化问题找到最优解的过程。和声算法现已广泛地应用于旅行商、函数优化问题等领域。和声算法的主要参数包括和声记忆库的大小()、和声记忆库考虑概率()、和声音调微调概率()、算法迭代次数（）。其具体步骤如下：

1)初始化优化问题()及算法的参数。

2) 随机产生个的初始解放入和声记忆库内，计算每个解的目标函数值。

3) 通过HS算法的记忆考虑、微调扰动、随机选择三个规则产生新解。

4) 判断新解是否优于原和声库中的最差解，若优于，则替换之，更新和声库。

5) 判断是否满足终止条件，若满足，跳出循环；若不满足，重复步骤3)和步骤4)。

1.2 优化和声算法

为了提高算法的寻优速度，优化和声算法（GAHS），利用高度并行和鲁棒性较强的遗传算法初始化和声记忆库，且在保留HS算法产生新解的三个规则的同时，增加遗传算法交叉操作产生新解。

GAHS的选择、交叉、变异等操作的具体细则如下。

①选择操作。采用锦标赛的方法，从种群中随机选择两个适应度较高的个体。

②交叉操作。随机从[0、1]中选择一个数rand1，如果rand1小于交叉概率（），则对选择操作得到的两个个体按式（1）、式（2）执行交叉操作：

（1）

其中，为交叉因子。

③变异操作。为了能够得到较高的精确度且具有微调能力，采用非均匀变异方法，即随机从[0、1]中选择一个数rand2，如果rand2小于变异概率（），则对交叉操作得到按式（3）或式（4）两种方案中随机选择一种进行变异。

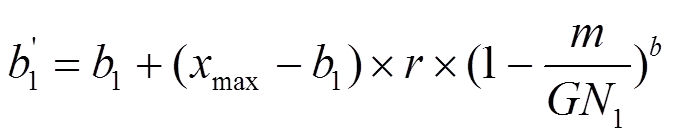
（4）

式中：_ma、分别为变量的上界和下界；为确定非均匀程度的参数。

GAHS的具体步骤如下。

1）初始化算法参数。算法参数主要包括种群的规模()、交叉概率()、变异概率()、遗传算法迭代次数()及、、。

为了提升算法的局部搜索能力及跳出局部最优值，GAHS中的变异概率（）采用式（5）动态变化。

2）初始化GAHS的和声记忆库

GAHS的初始记忆库的解向量是初始种群首先通过遗传算法的选择、交叉和变异操作，经过次迭代后产生大小为的新种群，再从新种群中选出最优的个个体。其具体步骤如下。

a)初始化种群。对配电网中的各条馈线和开关进行编码，然后根据FTU上传的故障信息随机建立一个种群。

b)计算步骤a)种群中每个解的目标函数()，利用本文中遗传算法的选择、交叉、变异操作对初始种群中的解进行次迭代，产生新解群。

c) 从新解群中找出最优的HMS个个体放入和声记忆库中，作为初始和声记忆库的解向量。

3）生成新解。对GAHS和声记忆库中的初始解向量利用记忆考虑、微调扰动和随机选择三个规则产生的新解与利用GA中的交叉操作产生的新解进行比较，保留好的解向量，生成新解。

4）更新HM。若新解优于和声库中最差解，则替换之；将最优的解放入和声记忆库。

5）算法的终止条件。判断是否达到预定的迭代次数，若是，则算法结束；否则重复3）和4）。

2 网络维度降阶

本文将配电网络看成度为1且以电源点为顶点的有源树和若干无源树枝组合的连通有向图。有源树包含配电网络中的所有电源。若配电网中发生故障时，无源树枝中故障电流均由有源树中的各个电源提供，所以在编码时去除无故障的无源树枝，这样很大程度上降低了解的维度，缩短了定位时间，从而提高定位效率。

图1为含24开关节点，3个DG电源，4条无源树枝的配电网，其中有源树为实线相连的网络结构，无源树枝为虚线相连的网络结构。若K处发生故障时，4条无源树枝中的各个开关均无故障电流通过，则此时可以剔除这4条无源树枝，这样FTU上传的故障信息的维数就由24维减少到了13维，可以很大程度上提升运算的速度和精度。

图1 含DG的配电网络图

Fig. 1 Distribution network with DG

3 优化和声算法的应用

配电网故障定位方法是对线路的状态和流过开关的故障电流信息编码后，根据FTU上传的实时故障电流信息与通过开关函数计算得出期望的故障电流信息，运用优化算法来评价目标函数的各个解的优劣程度，从而找出最优解，确定故障线路。其中流过FTU的故障信息为己知的参数，线路的状态为待求的参数。

3.1 状态参数

算法以参数的状态编码为运算对象，需要对参数进行状态编码。线路只有正常和故障两种状态，采用0和1二进制的编码方式，0代表线路正常，1代表线路故障。当FTU检测到的故障电流方向与该开关所定义的正方向相同时，开关的状态值取“1”；相反时，取“-1”；无故障状态时取“0”。

3.2 开关函数

基于含DG配电网的结构特点，定义网络中某一个开关的上游电源为与该开关距离最近的电源（当该开关到与其相邻的电源距离相同时，可以取其中的任一电源为其上游电源），网络中剩余的电源为该开关的下游电源。开关正方向为上游电源指向下游电源。这样对于网络中的任一个开关而言，只有一个确定的正方向。本文所定义的开关函数表示为

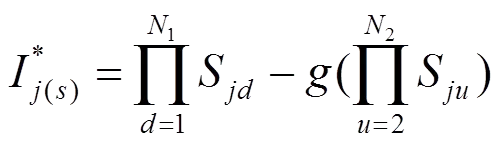
如图2所示为简单含DG配电网络，定义开关S、S以主电源S为上游电源，则DG、DG为下游电源；开关S、S、S以DG为上游电源，则主电源S、DG为下游电源；开关S、S、S以DG为上游电源，则主电源、DG为下游电源。以开关S为例，当线路C发生K短路故障时，其流过开关S的故障电流方向与假定的正方向相同，开关S的状态值I取“1”；而此时开关S的故障电流方向与所假定的正方向相反，所以，开关S的状态值I取“-1”。

图2典型DG配电网络故障定位分析图

3.3 评价函数

评价函数的构造能否准确符合所需解决问题的本质，对和声优化算法能否得到最优解有着决定性的影响。为了提高运算速度，防止在故障定位过程中出现误判或漏判的现象，根据故障定位的最小集理论对文献[14]中的目标函数进行改进，如下

3.4 计算步骤

针对图1所示配电网模型，应用网络维度降阶方法、优化和声搜索算法寻优求解的过程如下。

1）对图1中各开关节点和馈线区段编号，确定开关正方向。S、S以主电源S为上游电源，S、S、S、S、S、S以DG为上游电源，S、S、S、S、S以DG为上游电源，S、S、S、S、S、S、S、S、S、S、S以DG为上游电源。开关方向为上游电源指向下游电源。

2）根据配电网模型将网络划分为有源树和无源树枝的组合，并根据FTU上传的故障电流信息剔除无故障电流的无源树，确定解的维数。

3）初始化、目标函数及算法参数：优化问题的参数包括目标函数、开关函数，修正系数取0.5；GAHS的参数设置如下：交叉概率=0.85，种群规模=50，遗传算法迭代次数=500，和声记忆库大小=5，和声记忆库考虑概率=0.9，扰动概率=0.85，扰动量=4.5，GAHSA的最大迭代次数=2000。

4）初始化和声记忆库，对上传的故障信息通过式（6）将解转化为开关故障电流信息，再通过式（7）计算其目标函数值；最后利用GA进行次迭代后产生新的种群，从新种群中选出最好的个个体作为GAHS记忆库的初始解向量。

5）通过本文中GAHS新解的产生规则生成新和声。

6）判断新解是否优于原和声库中的最差解，若优于，则替换和声库中的最差解，更新和声库。

7）判断是否满足终止条件，若满足，跳出循环；若不满足，重复步骤5）和步骤6）。

4 算例分析

为了验证该算法的性能，对配电网在不同情况下出现的故障进行了仿真测试，仿真环境为：MatlabR2010a、处理器2 GB、内存为2 GB的PC，对图1所示的配电网模型进行算例分析，比较了GAHS与HS的性能。

4.1 故障信息正常下优化前后算法的性能比较

以图1含DG的配电网中的单故障K，双故障K、K两种情况为例，利用GAHS、HS分别对单故障K，双故障K、K两种情况连续运行程序100次，求出GAHS、HS算法实现故障定位的迭代次数和耗时，算出平均迭代次数和平均耗时。平均迭代次数和平均耗时的计算过程为：每次程序运行后，记录最优结果首次出现时和声算法已迭代的次数和已耗时间，然后将100 次的记录结果求平均值，即得到和声算法实现故障定位所需的平均迭代次数和平均迭代时间。

分析可知GAHS、HS两种算法对于含DG配电网单、双故障的准确率皆达到99%以上，其定位单、双故障所需的迭代次数、耗时统计结果如表1、表2所示。由表1、表2可知，GAHS平均的迭代次数皆少于HS算法，且GAHS的平均耗时明显低于HS的耗时平均值，表明GAHS相比HS能够更快地收敛于最优解，即GAHS的搜索效率明显优于HS。图3、图4为GAHS与HS分别对配电网单、双故障定位仿真的耗时曲线图。

表1GAHS与HS对电网单故障仿真统计表

Table 1 Simulation statistics of GAHS and HS for single fault in the grid

表2 GAHS与HS对电网双故障仿真统计表

图3 GAHS与HS对配电网单故障仿真的耗时曲线图

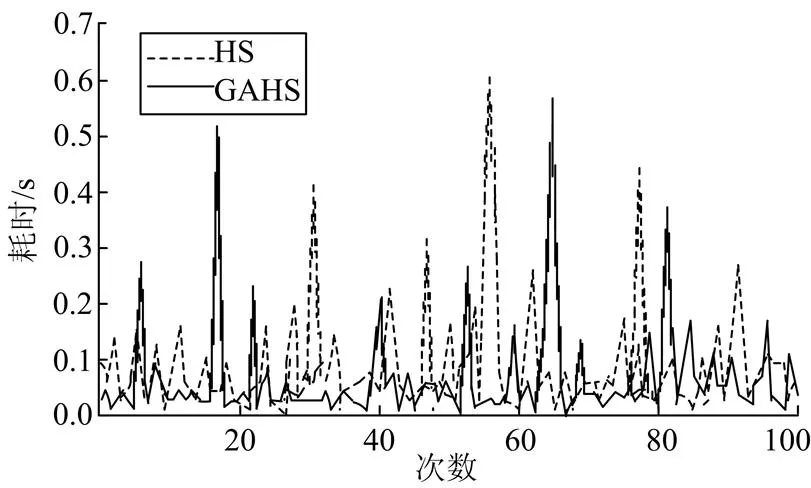
图4 GAHS与HS对配电网双故障仿真的耗时曲线图

4.2 信息畸变情况下GAHS与HS的准确率比较

以图1含DG配电网中的单故障K，且FTU上传的故障信息中开关S9发生畸变为例，利用GAHS、HS分别对其进行100次仿真，来验证GAHS算法的容错性和定位精度。此次实验分为5组，利用这两种算法分别对每组畸变的故障信息进行20次算例仿真。对配网中，K故障，开关S9信息畸变，FTU上传的故障信息为[11-1100010110011110001000]，运行程序。准确定位次数的统计结果如表3所示。由表3可知， GAHS对第四组准确定位的次数与HS的相同，但对其余四组准确定位次数均大于HS，且GAHS定位的准确率为98%，HS的准确率为89%。由此可知，GAHS相对于HS而言具有较强的容错性和较高的定位精度。

表3 HS与GAHS准确定位次数统计表

5 结论

为了提高含DG配电网故障定位的速度和容错性，利用高度并行、鲁棒性强的遗传算法来优化基本和声算法对初始化和声记忆库的过度依赖性，改进了和声算法中新解的产生方式，应用树区域划分法降低了求解的维度，根据最小集理论优化开关函数以提高容错性，分别利用优化前、后的和声算法对相同配电网模型进行寻优运算和分析比较，结果表明优化的和声搜索算法能够有效地提高算法收敛速度和故障定位精度，在信息缺失、畸变等情况下具有良好的容错性。

[1] 卫志农, 何桦, 郑玉平. 配电网故障区间定位的高级遗传算法[J]. 中国电机工程学报, 2002, 22(4): 127-130.

WEI Zhi-nong, HE Hua, ZHENG Yu-ping. A refined genetic algorithm for the fault sections location[J]. Proceedings of the CSEE, 2002, 22(4): 127-130.

[2] 文福拴, 邱家驹, 韩祯祥. 只利用断路器信息诊断电力系统故障的高级遗传算法[J]. 电工技术学报, 1996, 11(2): 58-64.

WEN Fu-shuan, QIU Jia-ju, HAN Zhen-xiang. A refined geneticalgorithm for fault section estimation using information from circuit breakers[J]. Transactions of China Electrotechnical Society, 1996, 11(2): 58-64.

[3] 徐玉琴, 张丽, 王增平, 等. 基于多智能体遗传算法并考虑分布式电源的配电网大面积断电供电恢复算法[J]. 电工技术学报, 2009, 24(5): 190-196.

XU Yu-qin, ZHANG Li, WANG Zeng-ping, et al. Algorithm of service restoration for large area blackout in distribution network with distributed generators[J]. Transactions of China Electritechncal Society, 2009, 24(5): 190-196.

[4] 齐郑, 乔丰, 黄哲洙, 等. 基于暂态分量遗传算法的小电流接地故障定位方法[J]. 电力系统保护与控制, 2014, 42(1): 34-39.

QI Zheng, QIAO Feng, HUANG Zhe-zhu, et al. Genetic algorithmfault location based on transient component for neutral point non-effective grounding system[J]. Power System Protection and Control, 2014, 42(1): 34-39.

[5] 李超文, 何正友, 张海平, 等. 基于二进制粒子群算法的辐射状配电网故障定位[J]. 电力系统保护与控制, 2009, 37(7): 35-39.

LI Chao-wen, HE Zheng-you, ZHANG Hai-ping, et al. Fault location for radialized distribution networks based on BPSO algorithm[J]. Power System Protection and Control, 2009, 37(7): 35-39.

[6] 周湶, 郑柏林, 廖瑞金, 等. 基于粒子群和差分进化算法的含分布式电源配电网故障区段定位[J].电力系统保护与控制, 2013, 41(4): 33-37.

ZHOU Quan, ZHENG Bo-lin, LIAO Rui-jin, et al. Fault-section location for distribution networks with DG based on a hybrid algorithm of particle swarm optimization and differential evolution[J]. Power System Protection and Control, 2013, 41(4): 33-37.

[7] 郑涛, 潘美玉, 郭昆亚, 等. 基于免疫算法的配电网故障定位方法研究[J].电力系统保护与控制, 2014, 42(1): 77-83.

GUO Tao, PAN Mei-yu, GUO Kun-ya, et al.Fault location of distribution network based on immune algorithm[J]. Power System Protection and Control, 2014, 42(1): 77-83.

[8] GEEM Z W, KIM J H, LOGANATHAN G V. A new heuristic optimization algorithm: harmony search[J]. Simulation, 2001, 76(2): 60-68.

[9] MAHDAVI M, FESANGHARY M, DAMANGIR E. An improved harmony search algorithm for solving optimization problems[J]. Applied Mathematics Computation, 2007, 188: 1567-1579.

[10] OMRAN M, MAHDAVI M. Global best harmonysearch[J]. Applied Mathematics and Computation, 2008, 198(2): 643-656.

[11] DAS S W, MUKHOPADHYAY A, ROY A, et al. Exp1oratory power of the harmony search algorithm: analysis and improvements for global numerical optimization[J]. IEEETrans on Power Systems, 2011, 41(1): 89-106.

[12] 韩红燕, 潘全科, 任文娟, 等. 基于遗传和声算法求解函数优化问题[J]. 计算机计算机应用研究, 2011, 27(5): 1723-1725.

HAN Hong-yan, PAN Quan-ke, REN Wen-juan, et al. Function optimization problem based on genetic harmony algorithm[J]. Application Research of Computers, 2011, 27(5): 1723-1725.

[13] 玄光男, 程润伟. 遗传算法与工程优化[M]. 北京:清华大学出版社, 2004.

XUAN Guang-nan, CHENG Run-wei. Genetic algorithms and engineering optimization[M]. Beijing: Tsinghua University Press, 2004.

[14] 刘蓓, 汪沨, 陈春, 等. 和声算法在含DG配电网故障定位中的应用[J]. 电工技术学报, 2013, 28(8): 1-5.

LIU Bei, WANG Feng, CHEN Chun, et al. Harmony algorithm for solving fault location in DG distribution network[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 1-5.

Application of harmony algorithm optimized for fault location in distribution networks with DG

GAO Yun-long, ZHOU Yu-sheng, PENG Pai, LIU Rang-jiao, AN Zheng-zhou

(College of Electrical Engineering and Information, Changsha University of Science and Technology, Changsha 410114, China)

In order to improve the speed and fault tolerance of the distribution network with distributed generator (DG), this paper uses highly parallel and robust genetic algorithm to solve the over-reliance on the initialized harmony memory of basic harmony algorithm, and improves the data processing way of harmony algorithm. According to the structure characteristics of the distribution network with DG, the "tree" division method is used to decrease the function solving degree. In order to improve the fault tolerance, the minimum set theory is used to improve fault location evaluated function. The optimized harmony search and basic harmonic algorithm are used respectively in the same distribution network fault location model for analysis and comparison. Results show that the optimized harmony search algorithm can effectively improve the convergence speed and precision, and it has good fault-tolerance as the lack or distortion of the fault information.

distributed generation (DG); distribution network; fault location; optimized harmony algorithm; evaluated function

TM711

A

1674-3415(2014)19-0026-06

2014-01-03；

2014-03-24

高云龙(1984-)，男，通信作者，硕士研究生，研究方向为电力系统继电保护与配电网自动化；E-mail：411406221@ qq.com

周羽生(1965-)，男，博士，教授，研究方向为电力系统继电保护与配电网自动化、高温超导电力技术、高电压绝缘与监测；

彭 湃(1989-)，女，硕士研究生，研究方向为电力系统继电保护与控制。

电力与交通安全监控及节能技术教育部工程中心资助项目（2011JG002）