无人复合三体船模Z形操纵运动初步研究

崔 健， 杨松林

(1.航运技术与安全国家重点实验室，上海 200135； 2. 江苏科技大学， 江苏 镇江 212003)

0 引 言

在高性能船的研究开发中，如何对各船型取长补短，进行复合，以获得最佳的性能，走“复合型船”的发展道路，是各国高性能船舶设计工作者的新课题。相关研究人员对此展开了一系列的理论分析和试验研究[1]。

江苏科技大学[2]发明的“一种复合三体船”包括主船体、位于主船体两侧的侧船体、连接主船体和侧船体的连接桥，侧船体下侧设有通过垂直支柱连接的水平翼。此外，该复合三体船还有侧体移动装置。

Konstantin[3]研究的混合三体船包括3个穿浪船体和考虑空气动力学的机翼式上层建筑。这种配置的特点是：相比高速渡轮和作战舰艇，其在高速航行时拥有更好的舒适感，并且效率更高。

海军工程大学的卢晓平[4]等人以三体船水动力型和K、T响应型(线性和弱非线性)操纵性运动方程为理论基础，以三体船重心运动轨迹微分方程组为数值仿真基础，采用仿真计算工具Matlab软件，对三体船回转运动轨迹、操纵性曲线以及Z型操纵试验曲线等操纵运动特性诸元进行了仿真计算。

哈尔滨工程大学的莫建[5]依据MMG分离建模思想，建立了波浪中船舶6个自由度操纵运动数学模型。首先，应用四阶定步长龙格库塔法在时间域内对波浪中船舶操纵运动方程进行了解算，利用FORTRAN语言开发了操纵运动仿真程序；随后通过波浪中船舶直航和静水中操纵运动实验证实了该数学模型的精度能够满足工程实际的要求；最后，在不同工况下计算得到了操纵运动实时仿真曲线，分析了船舶波浪中操纵运动规律以及回转过程中的船体及其关键点处的摇荡规律。

以上主要探讨的是三体船的两个侧船体纵向位置和横向位置变化对其操纵性能的影响。与常规单体船相比，三体船的回转性能有所下降，而其直线稳定性能则有所提高[6]。高性能复合三体船主要应用了空气动力学和流体力学原理，依靠随航速增加的水动力支持大部分的船舶重量，使得被托起后的船体只形成非常小的排水量。复合三体船主要复合小水线面船、水翼船、气垫船和冲翼艇等，属于此类船型概念的有“小水线面三体船”、“穿浪三体船” 、“水翼三体船”等。在设计复合三体船船型时，往往需要考虑以下几个方面：

(1) 要有优良的耐波性能；

(2) 能够向高速化发展；

(3) 载运能力要大；

(4) 经济性、安全性要好；

(5) 拥有优美造型和舒适的舱室空间环境。

1 复合三体船模

1.1 复合三体船模设计制作

设计的复合三体船的特征是在常规三体船的主船体和两侧船体上分别增设不同展弦比的水翼。增设水翼的作用归结为三点：

1) 在高航速情况下由于水翼升力作用使其船体抬升,减少船体的吃水，从而可以进一步提高航速。

2) 在主船体靠近艏部的水翼可以起到消波减阻的作用。

3) 主船体和两侧船体上的水翼设计成前后布置，水翼升力对船体重心的作用在一定程度上可以减缓船舶航行过程中的纵倾。

通过对三体船的主船体和侧船体的选型设计制作，最终得到复合三体船模(见图1)的主要参数(见表1和表2)。为了进一步探讨舵叶展弦比对船舶回转性能的影响，设计了六种不同展弦比的舵叶(见表3)。

图1 无人复合三体船模

1.2 无人艇智能控制系统

建立合理的硬件体系，利用可编程自动控制器(Programming Automatic Controller,PAC)完成主机、舵机、GPS(Global Positioning System)、三维电子罗盘等整个控制系统的闭环连接。PAC控制主机的转速，主机转速通过外部模拟量电压信号进行调节,以实现水面无人艇的推进性能；舵机的舵角根据PAC发出的调制信号进行控制,以实现无人艇的操纵性能；GPS和三维电子罗盘分别通过PAC的RS232接口和RS485接口反馈定位信号。为保证系统的统一性和连续性，将PAC内置时钟作为唯一的时间标准，最终通过编译PAC的自主控制程序接受和发送指令，实时调控无人艇的推进系统和操纵系统，实现无人艇的自主航行。无人艇数据分析处理系统的程序用Visual Basic.NET语言编制，可以实现友好的人机界面、方便的程序编制、灵活的升级改进、稳定的系统运行[7]。

表1 三体船模船型参数

表2 水翼要素

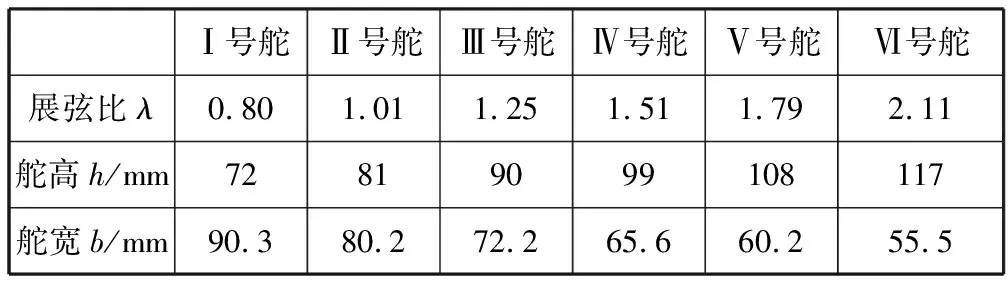
表3 六组不同展弦比的舵

2 操纵性仿真平台

2.1 操纵数学模型建立

由于船舶操纵运动线性数学模型有局限性，通常不可以用来预报各种情况下的操纵运动，尤其是船舶回转过程中的速降以及各种激烈的操纵运动等。因此，为了对船舶操纵运动(包括各运动参数、运动轨迹)进行比较精确的数学模拟，一般都采用非线性数学模型。常用有两种形式：

1) 将方程中的流体动力系数X、Y、N在直航状态附近对各运动参数作泰勒展开，即把X、Y、N表示为各种状态变量及其耦合项的泰勒级数之和。Abkowitz提出的三阶非线性模型就属于此种方式。

2) 按照各项流体动力的成因及其物理意义，将其表达为作用于船体、螺旋桨、舵上的流体动力及其相互间的干扰项，这样的数学模型称之为水动力模型。日本操纵运动数学模型小组(简称MMG)提出的MMG模型便是如此。

MMG数学模型具有如下特点：

图2 描述船舶运动的坐标系

(1) 将船体、螺旋桨、舵的各单独性能作为基准；

(2) 简洁地表达出船体、螺旋桨、舵之间的干扰；

(3) 尽量合理地表达出作用于船体上的流体动力。

数学模型建立的第一步为建立坐标系。船舶运动是动态的，便于分析，通常采用固定坐标系O-XY和运动坐标系G-ξη相结合的方式(只考虑平面运动)。

根据图2建立的坐标系，参考MMG模型得到复合三体船模的操纵运动数学模型，即运动方程组：

(1)

式(1)中:下标H、P、R分别为船体、螺旋桨和舵；λ11、λ22、λ66分别为船体的附加质量和附加惯性矩。

通过阅读苏兴翘[8]等人的著作和前期的研究[9]，对式(1)中相关参数及水动力系数进行处理。对复合三体船而言，由于其多体的特殊性，考虑先分别计算主体和侧体的附加质量，然后再进行叠加。在作无因次化分析时，以主体的相关参数作为基准。

2.2 仿真平台建立

针对复合三体船模的操纵运动模型，基于Visual Basic.NET语言平台，运用四阶龙格—库塔法进行数值求解，根据复合三体船模的主要参数以及航行参数计算得到相应的回转运动轨迹。回转过程中的首向角变化规律和漂角等参数同样可以求解得到。仿真平台(见图3)主要设置了参数模块、舵优化模块、回转模块和Z形操纵模块。

图3 仿真平台界面

3 操纵性试验

操纵性试验分为模型试验和实船试验两种，模型试验又可分为自由自航模型操纵性试验和约束模型操纵性试验两种。

3.1 Z形试验方法

无人复合三体船模Z形操纵试验主要开展了多种状态下的5°/5°、10°/10°和15°/15°Z形操纵试验(见表4)。试验方法见表4。

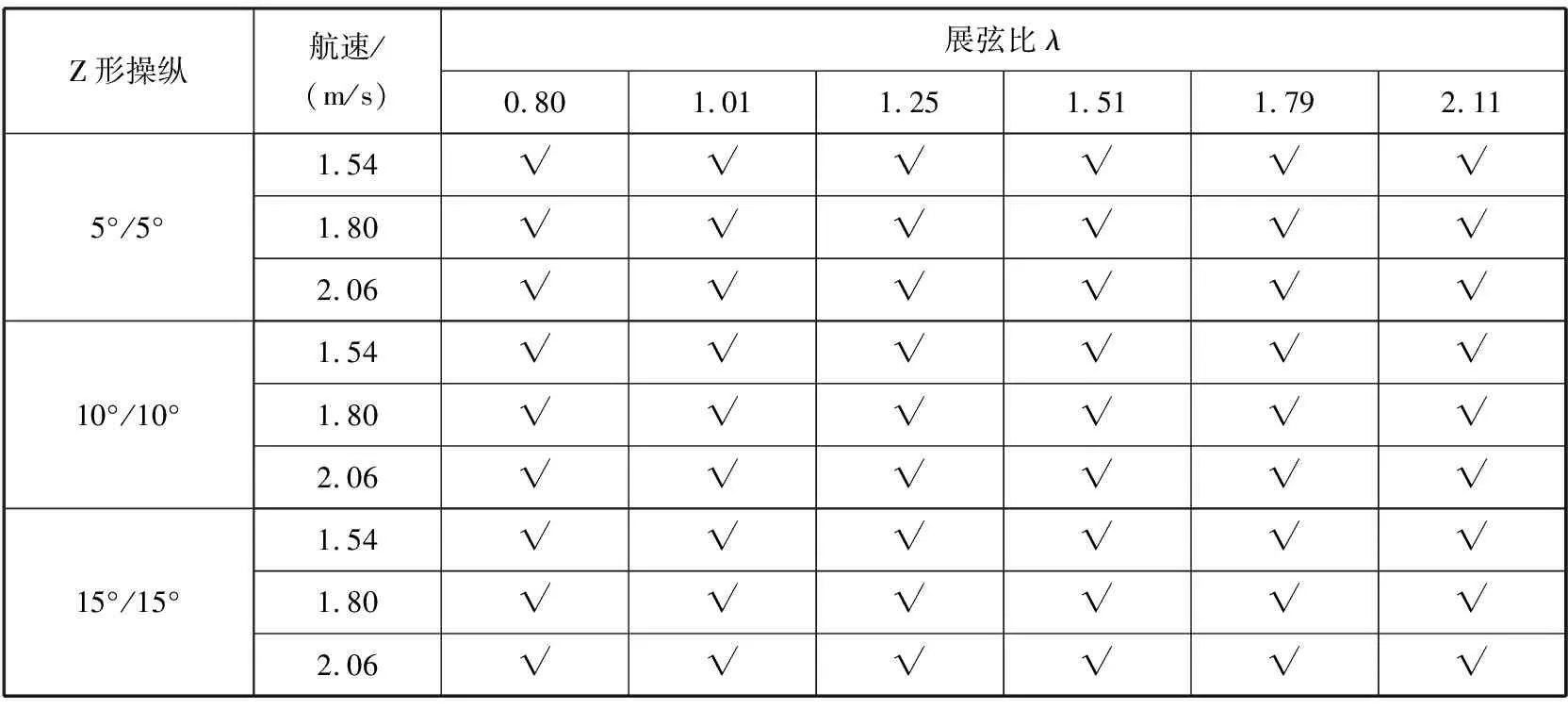
表4 Z形操纵试验方案

船模按预定航速直线航行达到稳定之后，三维电子罗盘记录船模当前的首向角ψ，控制中心PAC发出操舵指令将舵转到右舷5°(10°、15°)，作为第一次操舵；当三维电子罗盘检测船首偏离原首向角达5°(10°、15°)时，立即转舵到左舷5°(10°、15°)，作为第二次操舵；操上述反舵后，船仍朝原方向继续回转，但回转角速度逐渐减小，直到回转运动消失，然后船向左舷回转；当船首偏离原直航首向角达左5°(10°、15°)时，再操右舵角5°(10°、15°)，作为第三次操舵；上述过程一直持续到完成五次操舵以上为止。试验过程中，记录舵角和首向角的变化，用GPS采集三体无人艇的实时位置和实时状态数据信息。

3.2 仿真试验

依据上述无人复合三体船模操纵运动模式仿真平台，其仿真操作步骤如下：

1) 设置无人艇参数,主要包括主船体主尺度、侧船体主尺度、螺旋桨信息和舵叶信息。参数可以人工输入，也可以由建立的数据库进行选型。

2) 选择操纵仿真类型，主要包括回转仿真和Z形操纵仿真(见图4)。

3) 设置操纵试验仿真初始信息。进入仿真试验界面后需进行初始航行状态设置，主要包括初始位置、首向角、Z形回转角度、初始航速等。

4) 存储仿真数据。可以将仿真试验数据以文本格式和图片格式保存在指定的文件夹中，便于数据的进一步处理和分析。

5) 退出仿真。

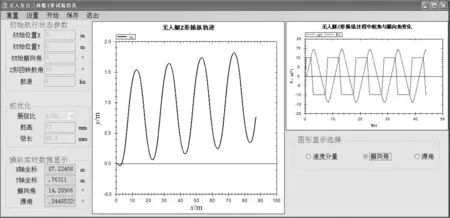
图4 Z形操纵仿真试验结果截图

3.3 仿真结果分析

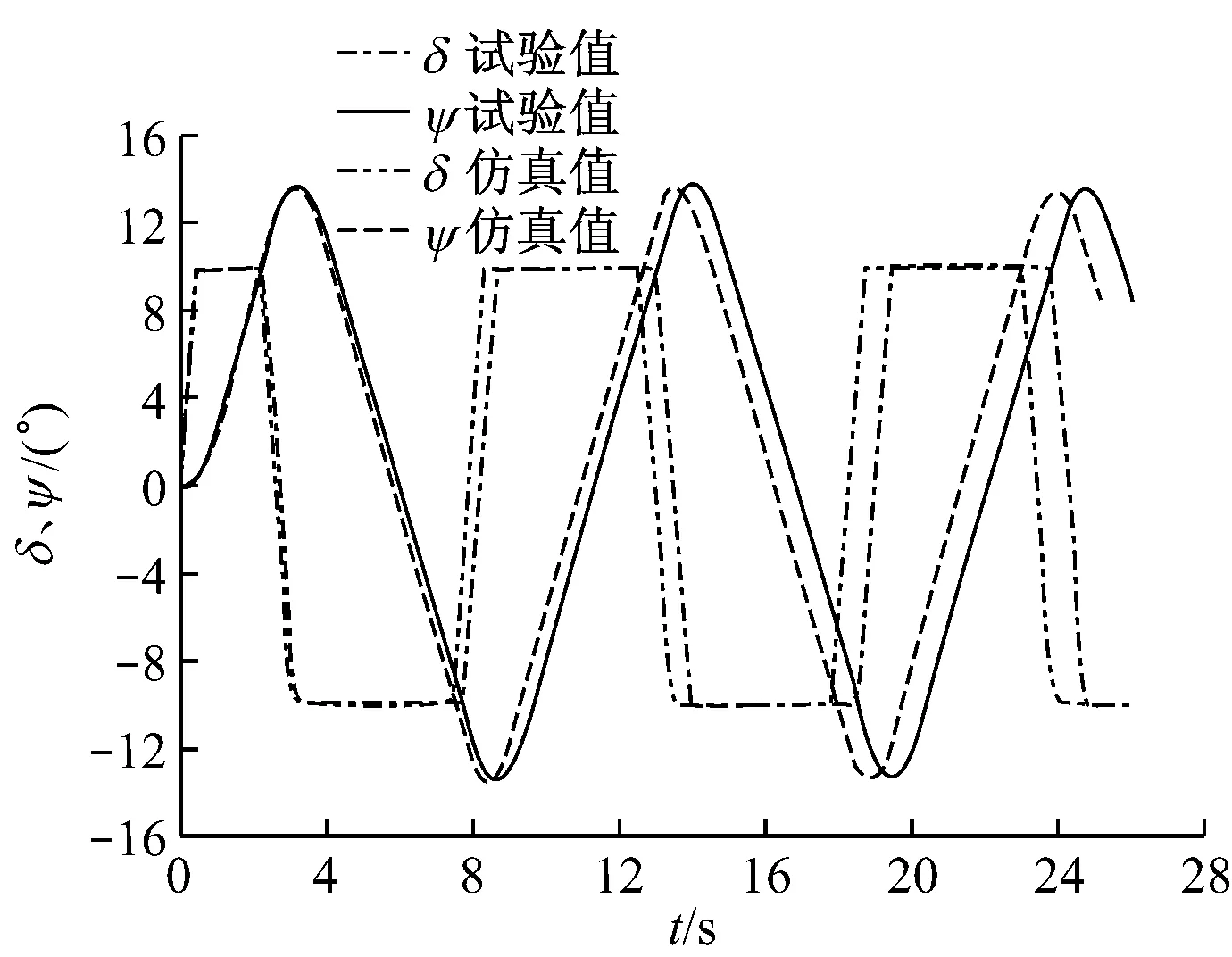
以1.80 m/s初始航速、不同舵叶展弦比下的10°/10°Z形操纵试验为例，将仿真结果数据与船模试验数据进行对比分析(见图5)，可见仿真结果与船模试验数据有着较好的一致性，从而证明了编译的仿真平台是可靠、有效的。

4 试验分析

4.1 系统辨识

系统辨识(System Identification)是根据系统的输入输出数据建立系统数学模型(Mathematical Model)的理论和方法，包括确定系统数学模型结构(Structure of Mathematical Model)和估计数学模型参数。

作为无人艇运动的控制量舵角δ(由舵角传感器测量)、螺旋桨转速n(由测速发电机测量)，以及能够测量的船舶前进速度u(由GPS记录测量)、航向角ψ(由GPS记录测量)、转首角速度r(由角速度陀螺仪测量)，对辨识算法而言都是输入量。辨识算法的输出量则是数学模型中建立的待辨识参数。

4.2 优化方法

遗传算法是以达尔文的生物进化论和孟德尔遗传变异理论为基础，模拟生物界进化过程，自适应、启发式、全局优化的搜索算法。传统的遗传算法存在局部搜索能力差和容易陷入早熟等问题。

混沌是自然界中一种普遍的非线性现象，具有随机性、遍历性和规律性。初始值的微小变化会引起系统行为的巨大变化，即混沌对于初值极为敏感。混沌优化算法的基本思想是把待求问题的解变换到混沌空间，利用混沌的上述特点进行搜索。该算法易于跳出局部极小，恰巧弥补了遗传算法易于陷入局部最优的缺陷[10]。

采用混沌遗传算法作为系统辨识的优化方法，其主要步骤如下：

(a) λ=0.8

(b) λ=1.01

(c) λ=1.25

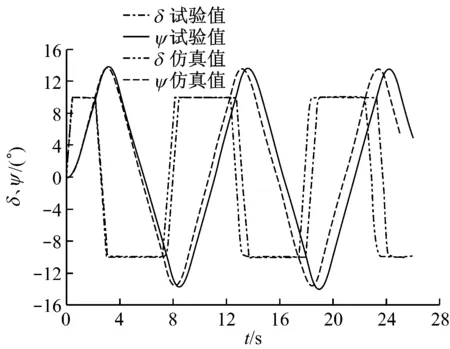
(d) λ=1.51

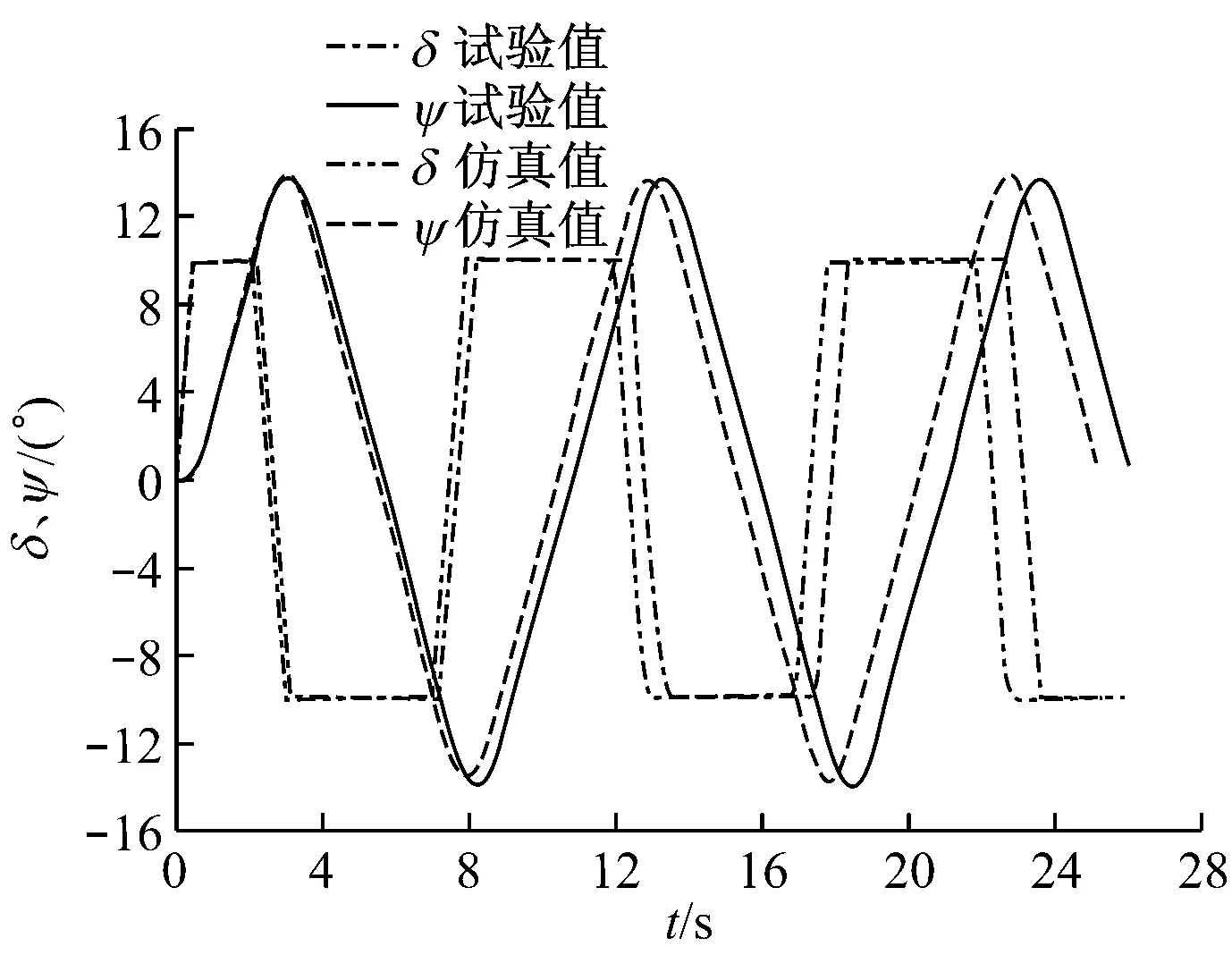
(e) λ=1.79

(f) λ=2.11

(1) 产生初始种群P(t),令迭代计数器t=1；

(2) 计算初始种群的适应度值；

(3) 按照给定的遗传算法进行选择、交叉、变异操作，生产下一代种群P′(t)；

(4) 对种群P′(t)中的个体按照适应度值进行从小到大排列，并取出适应度值较小的m个个体进行混沌映射与混沌迭代，生产新的m个个体；

(5) 对新的m个个体进行适应度值计算，并替代原种群中适应度值较小的个体，重新生成种群P″(t)；

(6) 令P(t+1)=P″(t)，计算种群P(t+1)的适应度值；

(7) 判断是否满足终止条件或判断是否达到预设的迭代次数。若不满足，则t=t+1，继续迭代计算；若满足，则结束迭代，输出当前的最优解，算法结束。

4.3 目标函数建立

从无人艇的实际操纵情况看，像回转试验一样长时间保持一定舵角的情况是不多的。通常是以比较小的舵角左右不断地操舵。无人艇Z形操纵运动正是模拟此种操纵。分析其试验结果，可以得到更符合实际操纵的资料。

采用5°/5°、10°/10°和15°/15°舵角进行Z形操纵试验，属于小舵角的偏转运动，运动幅度小，非线性系数α是不敏感系数，在数据处理时，可不考虑非线性影响。取KT方程作为系统辨识对象的数学模型。

根据系统辨识目的选择目标函数为：

(2)

式(2)中：T1、T2、T3、K为待辨识的参数；N为记录的次数。

4.4 辨识结果分析

经分析,各个待辨识参数的取值范围依次为：T1∈[-0.5,0.5]，T2∈[0,1.5]，T3∈[-0.5,0]，K∈[0,2]。取交叉概率为0.6、变异概率为0.02、种群大小为500、迭代次数为1 000进行计算(辨识结果输出见图6)。

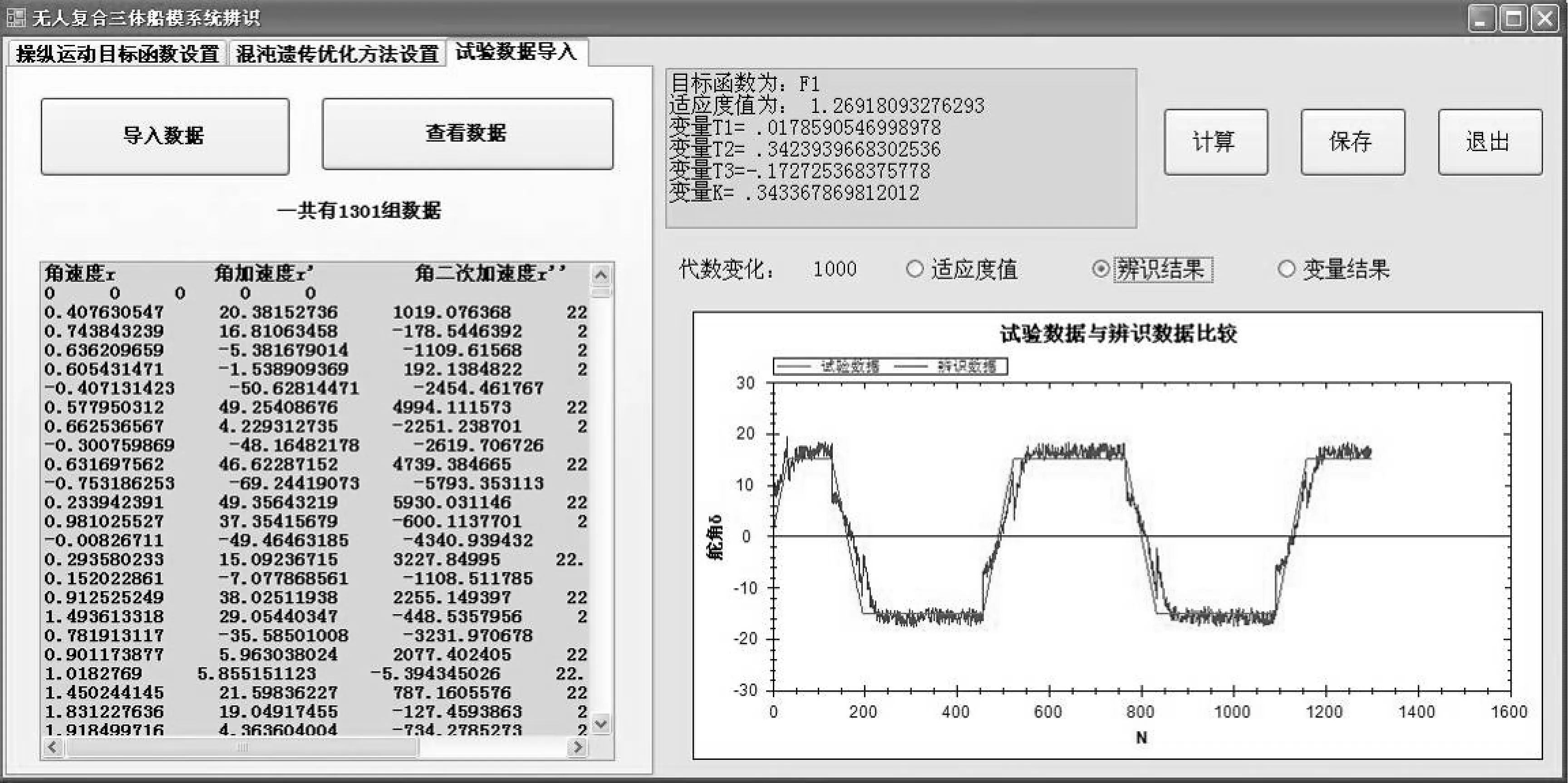
图6 辨识结果输出

现仅给出10°/10°的辨识结果(见表5)。其中K′、T′和p分别为回转性指数K与应舵指数T的无因次化结果以及“转首性指数”p值，计算方式为：

(3)

式(3)中：T=T1+T2-T3。

依据目标函数F的辨识结果可绘制同一航速下三种舵角的无因次化回转性指数K′与应舵指数T′随展弦比变化曲线图(见图7～图9)。转首性指数p值是将船舶的回转性能和航向稳定性进行综合考虑的参数指标，可以较为客观地反映船舶的操纵性能。绘制的p值变化曲线见图10。进一步分析可得如下结论：

(1) 无人复合三体船模的无因次化回转性指数K′随展弦比的增大而增大，说明在小舵角范围内增加舵叶的展弦比有利于提高船模的回转性能；

(2) 无人复合三体船模的无因次化应舵指数T′随展弦比的增大而减小，而T′值小则表示船舶的稳定性和跟从性好，即操舵后船舶能够较快地改变首向角，说明在小舵角范围内增加舵叶的展弦比有利于提高船模的跟从性；

(3) 无人复合三体船模的无因次化回转性指数K′随航速的增大而减小，同时应舵指数T′均随航速的增大而增大，说明航速的增大在一定程度上可能不利于提高船模的跟从性，也不利于提高船模的回转性能。

(4) 转首指数p值在试验范围内均>0.3，满足船舶转首性的要求，说明所选用的舵的性能与无人复合三体船模匹配合理。有时在一定程度上可适当减小舵面积，在满足操纵性要求的同时可以降低舵叶带来的阻力以及舵机的功率。同时，转首指数p值随展弦比的增大而增大，随航速的增大而减小，进一步说明在小舵角范围内舵叶的展弦比增大对复合三体船模操纵性而言是有利的，而航速的增大在一定程度上对复合三体船模操纵性而言是不利的。

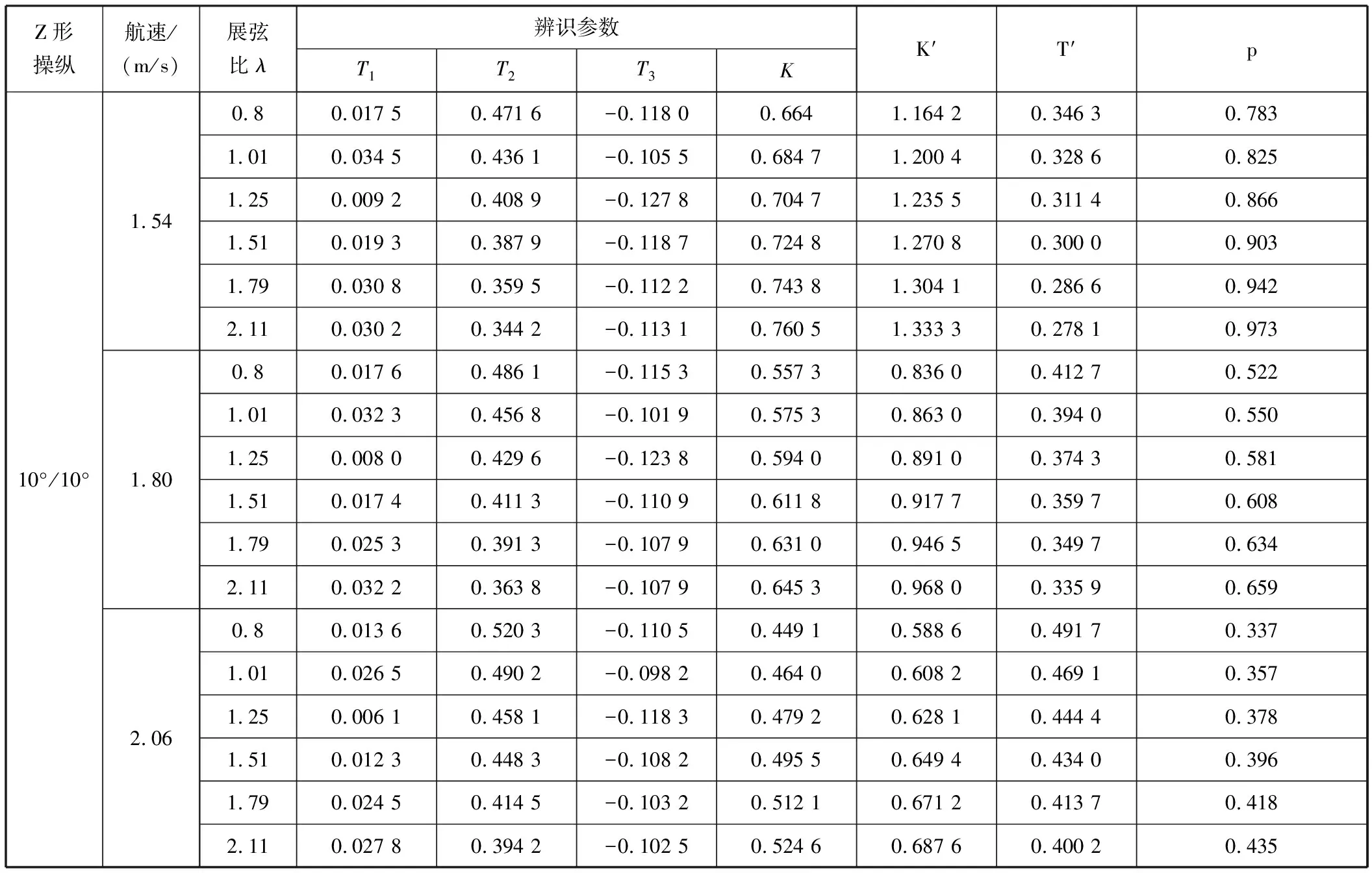
表5 10°/10°辨识结果

图7 5°/5°Z形操纵K′T′值变化曲线图

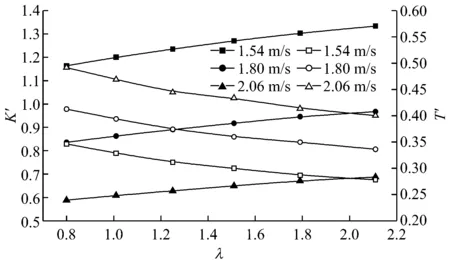
图8 10°/10°Z形操纵K′T′值变化曲线图

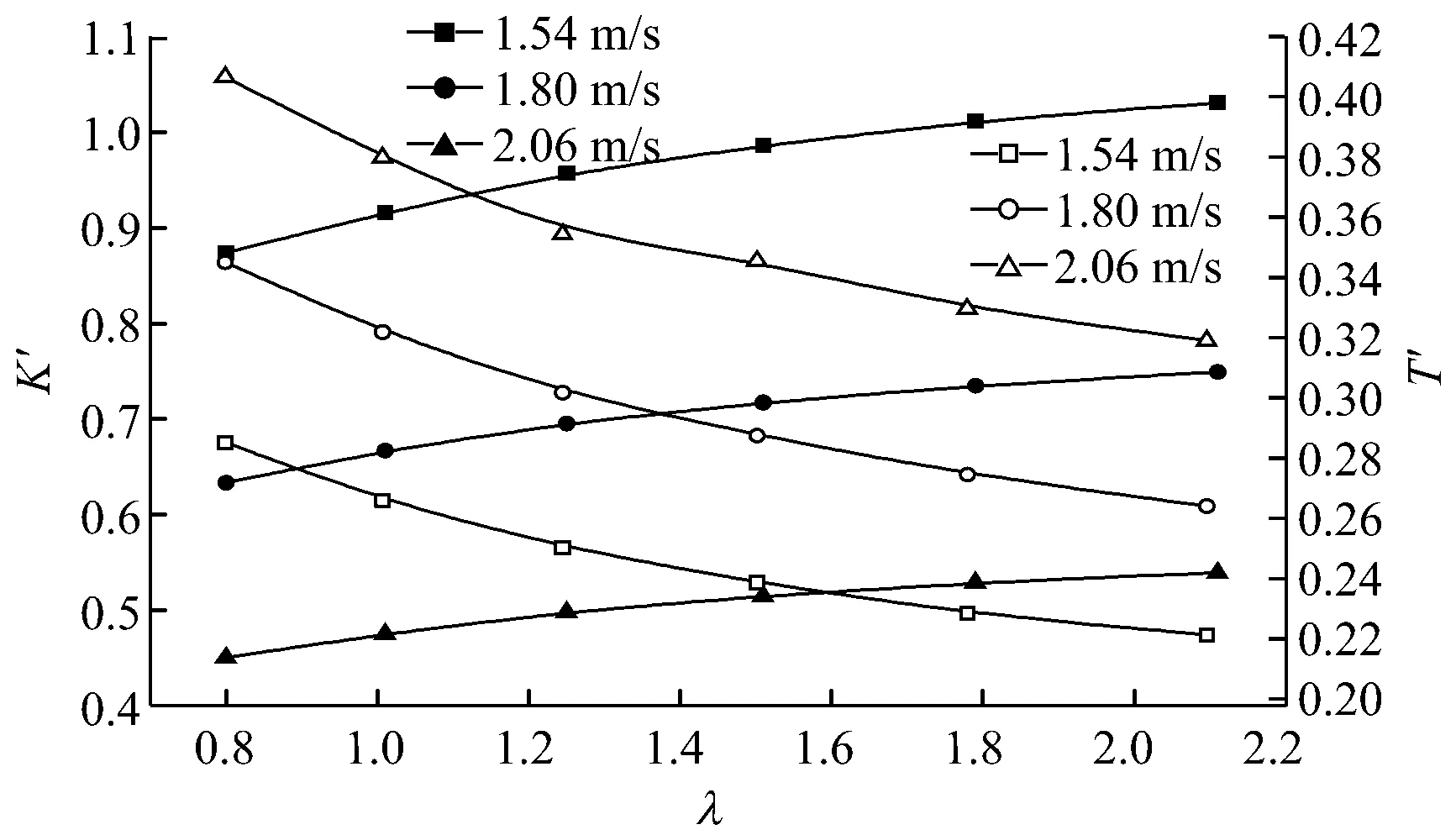
图9 15°/15°Z形操纵K′T′值变化曲线图

图10 转首指数p值变化曲线图

5 结 语

在常规三体船的主船体和侧船体上分别设计了水翼，以可编程自动控制器为核心设计完成了复合三体船模的无人化智能控制系统，构造并制作了一艘无人复合三体船船模，并开展了船模的操纵运动模式试验。运用Visual Basic.NET语言编写了基于MMG操纵数学模型的复合三体船模操纵性仿真平台。特别设计制作了六种不同展弦比的舵叶，并相应地开展了不同航速和不同舵角下的一系列船模Z形操纵试验。通过对比试验数据与仿真结果，验证了仿真平台的可靠性。取KT方程作为系统辨识对象的数学模型。利用基于混沌遗传优化方法编写的系统辨识程序对目标函数进行系统辨识得到了各个待辨识参数的值，并将辨识结果与试验结果进行了对比，验证了系统辨识程序的可靠性。在小舵角范围内，展弦比的增加使得复合三体船模的无因次化回转性指数增大即提高了船模的回转性能，无因次化应舵指数减小即提高了船模的跟从性。在小舵角范围内选择较大展弦比的舵叶有利与提高复合三体船模的操纵性能。进一步运用转首指数进行分析再次证明了上述观点，同时说明所选用舵的性能与无人复合三体船模匹配较为合理。

参考文献：

[1] 王中，卢晓平，詹金林. 高速三体船的水动力学和船型研究新进展[J]. 船舶力学，2011,15(7)：813-826.

[2] 江苏科技大学. 一种复合三体船. 中国，ZL200910032817.6[P]. 2009-10-21.

[3] Konstantin I. M，Victor A. D. Aerodynamic Characteristics of a Hybrid Trimaran Model [J]. Ocean Engineering，2007(34):3-4.

[4] 卢晓平，姚迪，王波. 三体船操纵性计算与特性分析[J]. 海军工程大学学报，2009,21(1)：47-53.

[5] 莫建. 波浪中船舶六自由度操纵运动数值仿真[D]. 哈尔滨：哈尔滨工程大学，2009.

[6] 卢晓平，姚笛，王中. 三体船操纵特性计算机数值仿真[J]. 中国舰船研究，2010,5(3)：1-7.

[7] Jian Cui, Pengyu Wang, Songlin Yang. System Identification on Rotation Motion Pattern of Trimaran Unmanned Surface Vessel[C]. 2010 International Conference on Progress in Informatics and Computing.

[8] 苏兴翘，高士奇，黄衍顺. 船舶操纵性[M]. 北京：国防工业出版社，1989.

[9] 崔健. 具有一定避碰功能的无人复合三体船模操纵运动模式分析研究[D]. 镇江：江苏科技大学，2013.

[10] 高延峰，许瑛. 混沌遗传模拟退火组合算法性能研究[J]. 计算机应用与软件，2008，25(11)：238-240.