病态不等式约束模型的正则化算法研究
2014-08-16陶叶青施龙香
杨 娟,陶叶青,施龙香
1.中国矿业大学环境与测绘学院,江苏徐州,221008;2.宿州学院地球科学与工程学院,安徽宿州,234000
病态不等式约束模型的正则化算法研究
杨 娟1,2,陶叶青2,施龙香2
1.中国矿业大学环境与测绘学院,江苏徐州,221008;2.宿州学院地球科学与工程学院,安徽宿州,234000
应用先验信息建立不等式约束模型是求解模型参数的有效途径,通过罚函数与零权和无限权的思想确定不等式约束模型的最小二乘解时,病态法方程矩阵对不等式约束模型解的稳定性存在一定影响。根据吉洪诺夫正则化方法的基本思想,对病态不等式约束模型的正则化算法进行阐述,并对应用岭迹法确定岭估计参数、通过迭代计算确定无限权数值来克服不等式约束模型病态性的算法进行了讨论。在此基础上,用实例对算法进行了验证,结果表明:应用岭迹法确定岭估计参数能够有效消除病态不等式约束模型对模型参数求解的影响,吉洪诺夫正则化的方法适用于对病态不等式约束模型的正则化。
不等式约束平差;不适定问题;正则化;无限权
1 研究背景
应用先验信息建立对参数不等式形式的约束,在最小二乘准则下建立平差模型,称为不等式约束平差。随着测量技术的进步和已有测量数据的大量积累,参数的先验信息也在不断丰富。如何应用先验信息建立科学的不等式约束模型,提高与改进平差精度,越来越受到国内外学者的关注。文献[1]用线性规划中的线性补方法求解具有约束的最小二乘问题;文献[2-5]对在大地测量领域中的变形检验、GPS数据处理、大地控制网的优化等方面不等式约束的应用进行了相关分析,并取得一定成果;文献[6-8]对不等式约束的具体解法进行了研究,并且用Bayes和罚函数等方法来实现不等式约束的算法。
应用不等式约束,在含有误差的观测量矩阵求得可靠解算结果的时候,并没有考虑到观测量系数矩阵的病态性。而应用最小二乘准则建立平差模型,病态的系数矩阵会因观测量的微小变化导致解算结果的不稳定。解决模型的病态性一直是测量中不适定问题讨论的焦点,文献[9-12]对病态模型的正则化方法进行了相关分析,并就选权似合法、改进最小二乘估计法、谱修正迭代法等方法解决病态问题的算法进行了详细阐述,而对于解决不等式约束模型的病态性问题没有太多关注。
本文在前人研究基础上,应用罚函数与零权和无限权的思想获得不等式约束平差广义最小二乘解,对不等式约束算法中法方程矩阵的病态性和克服不等式约束模型病态性的正则化算法进行探讨。
2 不等式约束模型与正则化算法
2.1 不等式约束模型的算法
间接平差模型:
V=BX-L
(1)
最小二乘准则:
VTPV=(BX-L)TP(BX-L)=min
(2)
解为:X=(BTPB)-1BTPL
(3)
不等式约束的模型可表示为:
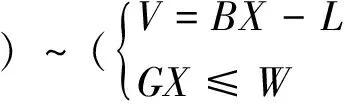
(4)
上述各式中,L为观测值;V为观测值改正数;B为参数X的系数矩阵;G为行满秩矩阵;W为常量,是对参数X解的约束。
不等式约束模型的解可通过遗传算法、凸二次规划等方法来实现[13-14],运用罚函数与零权和无限权的思想,将不等式约束转化为等式约束的算法则变得更加直观[8,15]。令:
V′=GX-W
(5)
当V′≤0时,参数X满足不等式约束,则不等式为无效约束;当V′≥0时,参数X不满足不等式约束,则不等式为有效约束。令:
P(x)= V′TP′ V′
(6)
P(x)为罚函数,当V′≤0时,即不等式为无效约束时,罚函数值为零;当V′≥0时,即不等式为有效约束时,罚函数值不为零。P′为罚函数P(x)的权值。
罚函数P(x)的取值通过定义零权和无限权实现,令:
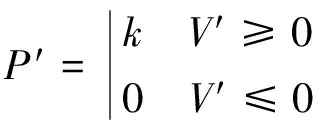
(7)
不等式为有效约束时,权值P′取一很大数值k;不等式为无效约束时,权值P′取值为零。不等式约束模型通过优化计算中的罚函数方法转化为无约束最优化问题:
φ(X)=VTPV+V′TP′V=min
(8)
不等式约束模型的广义最小二乘解为[8]:
X=(BTPB+GTP′G)-1(BTPL+GTP′L′)
(9)
式中L′=W。根据罚函数定义不等式约束模型,广义最小二乘解是通过迭代算法来实现的:首先应用不等式约束的间接平差模型获得最小二乘解;然后将最小二乘解代入约束不等式(如果满足条件则定义罚函数的权P′为零,如果不满足条件则定义P′为一较大数值k);再将定义的P′值代入式(9),求出广义最小二乘解(如果广义最小二乘解不满足约束不等式,则重新定义P′并进行迭代计算)。
2.2 病态性与正则化算法
测量数据处理的病态问题是指测量模型的解不稳定,引起病态问题的主要因素有两个方面:一方面,建立平差模型过度参数化,使得参数之间有一定的复共线性,导致模型病态;另一方面,测量数据不足,导致模型病态。病态模型的直接体现是间接平差模型(式(1))的解的法矩阵BTPB为奇异矩阵。目前,测量中不适定问题都可以通过吉洪诺夫(Tikhonov)正则化法[9]来求解,其实质是增加约束、补充先验信息,来克服不适定性。欧吉坤根据Tikhonov正则化的思想,给出平差模型解的统一形式[11]:
X=(BTPB+βPX)-1BTPL
(10)
式中,β为正则化参数;PX为稳定泛函。a、PX不同形式表示不同的平差模型,当β=K,PX=I时,表示岭估计。K为岭参数,I为单位阵,岭估计可以表达为:
X=(BTPB+KI)-1BTPL
(11)
不等式约束模型的迭代算法在实现过程中,如果法矩阵BTPB奇异,最终也会导致模型的广义最小二乘解的不稳定,因此,在不等式约束算法中同样存在着病态问题。不等式约束模型的病态问题可以通过Tikhonov正则化算法解决。
不等式约束模型是应用参数的先验信息建立的对参数具有不等式约束性质的模型,约束条件(GX-W)具有增加约束、补充先验信息的作用,这与Tikhonov正则化思想有相通之处。约束条件(GX-W)在模型的广义最小二乘解中通过无限权矩阵GTP′G实现,通过定义无限权矩阵GTP′G的取值来克服不等式约束模型的病态问题。
GTP′G中,矩阵G是关于参数X的约束不等式的系数阵,其形式固定,不能确定系数阵G对法矩阵BTPB的病态性是否有修正作用。应用罚函数P(x)求取不等式约束模型的广义最小二乘解,P(x)通过定义零权和无限权P′(式(7))实现。权P′应用迭代算法实现取值,数值不固定。通过定义权阵P′的值来实现GTP′G对法矩阵BTPB病态性的修正。定义P′的取值为岭迹法确定的岭参数K的解集与罚函数P(x)的无限权阵P′的k集(式7)的交集:
P′={k}∩{K}
(12)
上述算法实现的步骤:首先根据岭迹法确定模型的最小二乘解与岭参数K;然后将最小二乘解代入约束不等式(如果不满足条件,K值为无限权值P′的初值);再将P′值代入式(9),求出广义最小二乘解(如果广义最小二乘解不满足约束不等式,则对岭参数K重新取值,并进行迭代计算)。
3 实 验
应用文献[16]中的算例,算例中有10个观测值,3个未知参数[XYZ]T,其真值为[10 15 6]T。参数系数阵B与观测值L如表1。当矩阵条件数大于100时,判定矩阵呈病态性。法矩阵BTB的条件数为1740,呈病态性。
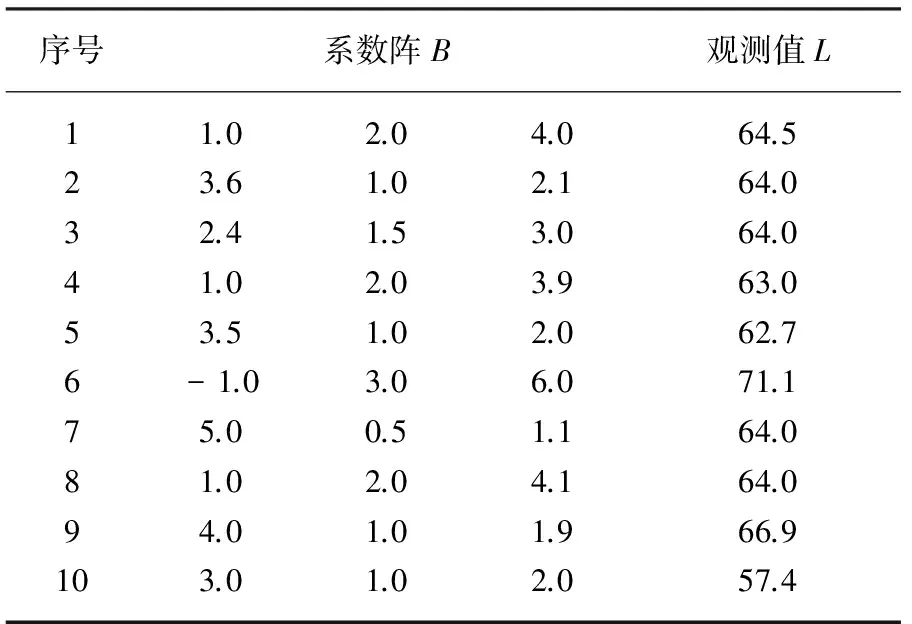
表1 系数阵B与观测值L
根据参数的真值,构造不等式约束模型的不等式系数阵G与约束值W,其值分别为:
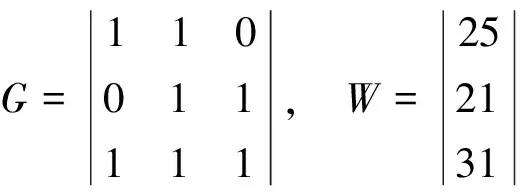
应用病态不等式约束模型的正则化算法,根据岭迹法确定岭参数进行迭代计算,获得广义最小二乘解集、参数的方差与点位均方向方差[17](表2和图1)。
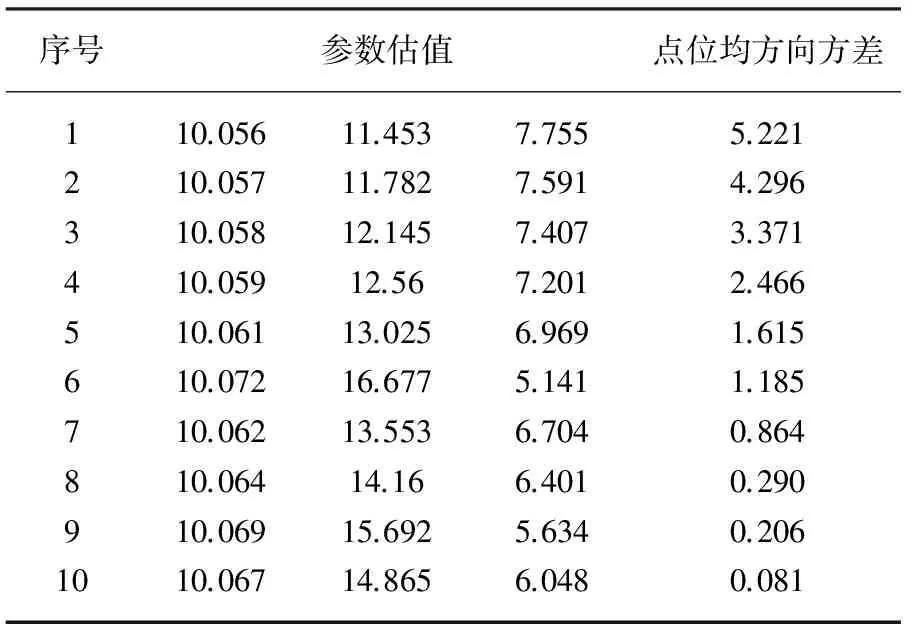
表2 参数解集与方差
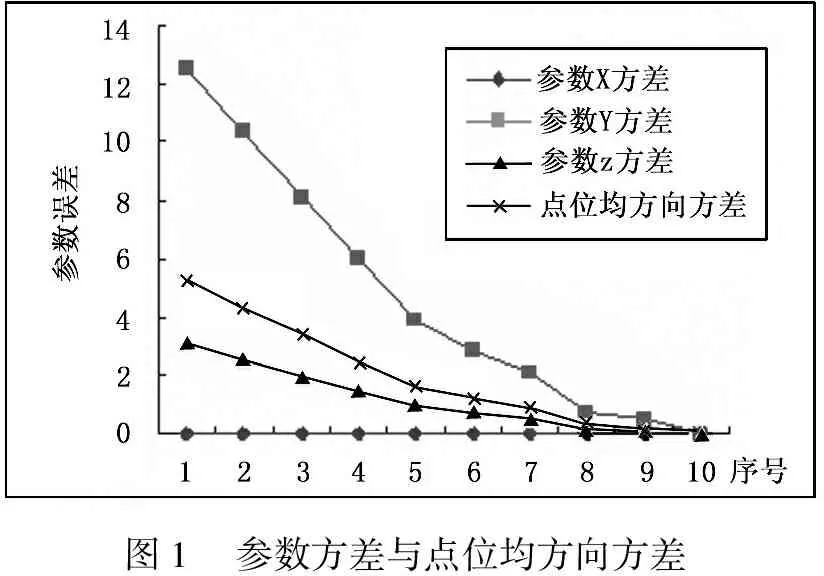
图1 参数方差与点位均方向方差
算例表明,应用罚函数与零权和无限权的思想获得不等式约束平差的广义最小二乘解,对于法方程系数矩阵存在的病态性,可以通过定义无限权P′来克服。无限权P′的数值大小由岭迹法确定的岭参数K通过迭代算法确定。
4 结束语
对于应用参数先验信息、在最小二乘准则下建立的不等式约束平差,通过不等式增加对参数的约束、补充先验信息,能够克服平差模型广义最小二乘解的不适定性。应用岭迹法确定岭参数、通过迭代计算确定无限权的方法,能够实现病态模型的正则化。算例表明,应用罚函数与零权和无限权的思想计算不等式约束平差模型的广义最小二乘解,运用正则化算法,能够克服法矩阵的病态性,得到收敛的参数解。
[1]Judge G G,Takayama.Inequality Restrictions in Regression Analysis[J].American Economic Review,1966,61:166-181
[2]Schaffrin B.Ausgleichung mit Bedingungs-ungleichungen[J].AVN,1981,88(6):227-238
[3]Koch K R,Riesmeier K.Bayesian Inference for the Derivation of Less Sensitive Hypothesis Tests[J].Journal of Geodesy,1985,59(2):167-179
[4]Remondi B W.Real-time Centimeter-accuracy GPS:Initializing While in Motion (Warm Start Versus Cold Start)[J].Navigation,1993,40(2):199-208
[5]Ueno M,Santerre R,Langelier D,et al.Improvement of GPS Ambiguity Resolution Using H-eight Constraint for the Support of Bathymetric Surveys[C]∥Proceedings of the IAIN/ION Conference. San Diego:[s.n.],2000:842-850
[6]Zhu J J,Santerre R,Chang Xiao-wen.A Bayesian Method for Linear Inequality Constrained A-djustment an Its Application to GPS Positioning[J].Journal of Geodesy,2005,78(9):528-534
[7]Peng J H,Zhang H P,Shong S L,et al.An Aggregate Constraint Method for Inequality-constraine-d Least Squares Problem[J].Journal of Geodesy,2006,79(12):705-713
[8]朱建军,谢建.附不等式约束平差的一种简单迭代算法[J].测绘学报,2011,40(2):209-212
[9]Tikhonov A N,Arsenin V Y.Solutions of III-Posed Problems[M].New York:Wiley,1977:89-95
[10]欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法[J].测绘学报,2004,33(4):283-288
[11]王新洲.在无偏估计类中改进最小二乘估计的方法[J].武汉测绘科技大学学报,1995,20(1):46-50
[12]沈云中,许厚泽.不适定方程正则化算法的谱分解式[J].大地测量与地球动力学,2002,22(3):10-14
[13]朱建军,欧阳文森,文小岳.基于遗传算法解决附有不等式约束的最小二乘平差问题的研究[J].工程勘察,2006(3):61-64
[13]宋迎春,左廷英,朱建军.带有线性不等式约束平差模型的算法研究[J].测绘学报,2008,37(4):433-437
[15]欧阳文森,朱建军.经典平差模型的扩展[J].测绘学报,2009,38(1):12-15
[16]杨元喜.自适应抗差最小二乘估计[J].测绘学报,1996,25(3):206-211
[17]菜剑红.一种新的点位误差度量[J].测绘学报,2009,38(3):276-279
(责任编辑:汪材印)
2013-02-10
安徽省优秀青年人才基金项目“皖西南地区滑坡动态变形数据处理模型及其稳定性研究”(2013SQRL085ZD);安徽省煤矿勘探工程技术研究中心平台项目“地矿3维GIS模型的构建及可视化、矿区CORS系统坐标转换模型及其适用性研究”(2014YKF04、2014YKF08);安徽省大学生创新创业训练项目“工矿区与高层建筑物沉降监测数据分析系统的设计与实现”(AH201310379047)。
杨娟(1984-),女,江苏徐州人,博士研究生,助教,主要研究方向:测量数值处理。
10.3969/j.issn.1673-2006.2014.07.027
P208
A
1673-2006(2014)07-0087-03
