基于估距方式分类的无线传感器网络定位算法*

黄智勇 张欣

(重庆大学 通信工程学院，重庆 400044)

定位技术是无线传感器网络的应用基础问题之一.在其定位模型中，通常将节点分为锚点(或称为信标节点，具有自主定位能力的节点)和未知节点(它们通过获取锚点的相关信息来确定自己的位置)［1］.现有针对传感器网络的定位算法大致可以分为基于测距的算法和无需测距的算法两类.由于无需测距的算法仅根据网络连通性就可以实现定位，因此该类算法具有抗干扰能力强、硬件成本低等优点，其中距离矢量跳距(DV-Hop)算法是无需测距算法的典型代表［2-3］.

DV-Hop 算法用平均跳距与锚节点间最小跳数的乘积来近似表示未知节点到锚节点的距离［3］.由于未知节点受地形、环境和气候等因素的影响，故其分布不均匀，导致估距计算存在较大的误差，使定位精度下降;平均每跳距离存在一定的误差，当未知节点到锚点间的跳数较大时，误差的累计效应会使定位精度进一步降低.

为提高DV-Hop 算法的定位精度，文献［4-5］中使用接收信号强度作为定位的辅助条件，但增加了硬件成本;文献［6］中提出了针对三边定位法的锚点筛选依据，但该方法直接忽略某些不满足条件的锚点，故不能有效利用这些锚点信息;文献［7-8］中提出了跳距加权的方法以提高定位精度;文献［9-10］从优化通信半径和锚点部署的角度来提高定位精度;文献［11］中提出了基于最小二乘法的等比例映射的定位方法，通过构建虚拟锚点来增加定位精度，但此方法对锚点与未知节点的分布有一定的要求.根据文献［12-13］中对未知节点进行分类处理的思想和文献［15-16］中的加权思想，文中提出了基于估距方式分类的无线传感器网络定位算法.

1 改进的DV-Hop 算法

针对传统DV-Hop 算法在估算距离时因存在较大误差而导致定位精度不高的问题，文中做了如下改进:①引入最优辅助估距锚点，并将距离估算分为3 类分别计算，以提高估距精度;②在三边定位法中引入“非线性－跳数”加权因子，使用该因子对估计坐标进行加权处理以解决三边定位法容易产生镜像坐标的问题.

1.1 估距方式的改进

从统计规律和文献［12］的论述可知，当某个未知节点处于两锚点间的最小跳数路径上时，使用这两个锚点间的平均跳数来计算这个未知节点到两个锚点间的估计距离，所得到的结果更为准确.因此，文中依据能否寻找到一个锚点，使得它与待估距锚点间的最小跳数路径完全包含或者部分包含当前所需估算的距离来对估距方式进行分类，使未知节点能够针对当前所需估算的距离选择与之相关的平均每跳距离，从而减小估距误差.如图1 所示，A(i)、A(j)、A(k)为3 个 锚 点，S(p)、S(q)、S(t)、S(l)、S(r)为5 个未知节点，连接线长度表示实际跳距，p为未知节点的ID，i 和j 分别为锚点的ID，则可用HNp，i表示未知节点S(p)到锚点A(i)的最小跳数，p，i表示S(p)到锚点A(i)的估计距离，HNj，i表示两锚点A(i)与A(j)间的最小跳数，di，j表示A(i)与A(j)间的实际距离，并有如下3 种估距方式.

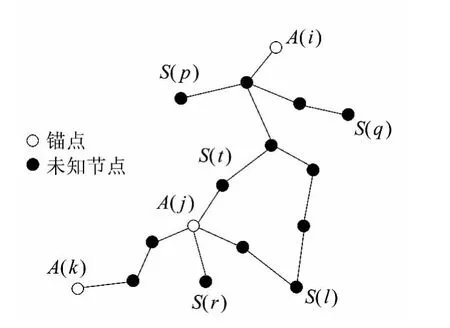
图1 锚节点分布示意图Fig.1 Schematic diagram of distribution of anchor and unknown nodes

(1)类型I.未知节点S(t)需要估算其与锚点A(i)间的距离.观察图1 可以发现，S(t)在锚点A(i)与A(j)间以及A(i)与A(k)间的最小跳数路径上.依据经验法则、两锚点间的跳数越小则两点间的线性度越好［12］，以及锚点间的已知直线距离及最小跳数路径可作为估计距离的相关约束条件［13］，文中采用如下更能准确反映S(t)到A(i)的平均每跳距离:

(2)类型II.当前需要测量S(r)到A(i)间的距离，但不存在任何一个锚点使得S(r)在A(i)与该锚点间的最小跳数路径上，即不满足估距方式I 的要求.观察图1 可知，S(r)到A(i)间的跳数由两部分组成，即HNr，i=HNr，j+ HNj，i，若以HSi，j作为平均跳距，则在式(1)等号两边同时乘以HSi，j，可得

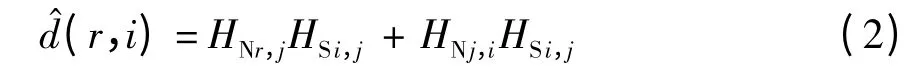
将di，j=HNj，iHSi，j代入式(2)可得

而两锚点间的距离di，j可由锚点A(i)与A(j)的坐标直接得出，不受A(i)与A(j)间未知节点的分布的影响.这样可以极大地减少由平均每跳距离产生的误差累计效应.根据文献［13］，由于未知节点S(r)不位于A(i)与A(j)之间的最小跳数路径上，故式(3)中的HSi，j无法反映S(r)到A(j)的每跳距离.实际上未知节点S(r)不位于图中任何两锚点间的最小跳数路径上，任意两锚点间的每跳距离与S(r)到A(j)的跳距不相关.为了尽量减小估算距离的均方误差，文中引入全局每跳距离作为未知节点S(r)到锚点A(j)的平均每跳距离，即

式中，As为锚点ID 的集合，当i=j 时，di，j= 0，HNi，j=0.从文献［15］的论述及统计学的角度分析，使用全局每跳距离的好处是:用尽量多的样本信息去估计未知参数的平均值，以降低均方误差.故未知节点S(r)到锚点A(i)的估计距离可表示为

此时称A(j)为估算S(r)到A(i)间距离时的类型II最优辅助估距锚点.由此可得类型II 估距方式的核心思想:当不满足类型I 的估距条件时，寻找辅助估距锚点，使得该锚点处于未知节点与待估距锚点间的最小跳数路径上，这样就可以利用该锚点和待估距锚点间的已知直线距离.同样地，当存在多个满足该条件的锚点时，应当选择与未知节点跳数最小的锚点作为类型II 的最优辅助估距锚点.当不存在这样的锚点时，直接进行类型III 的估距计算.

(3)类型III.如图1 所示，当估算未知节点S(q)到锚点A(i)间的距离时，q，i均不满足类型I 与II 的估距条件.实际上未知节点S(p)、S(l)、S(q)的存在与否对任意锚点的平均跳距均不产生影响.故任意两锚点间的平均跳距均不能有效表示S(q)到A(i)间的跳距.因此直接使用全局平均每跳距离进行类型III的距离估算，即

可以看出，类型III 的节点分布是排除类型I、II后其他分布情况的总和，故3 种估距方式对所有可能的分布情况进行了归纳，任意节点的任意一次估距计算均可归纳为其中的一种.则ID 为x 的未知节点到ID 为y 的锚点间的估计距离可表示为

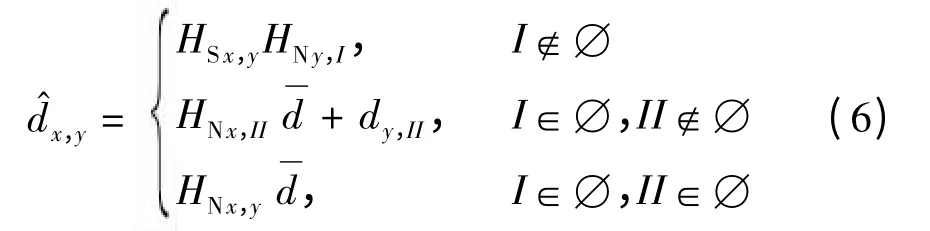
结合式(1)、(4)可求得S(x)到A(y)间的估计距离.需要指出的是:为了实现文中所提出的估距分类方法，每个锚点既要向网络中发送各自的位置坐标，又要发送该锚点到其他锚点的最小跳数表，故会增加一定的通信开销.ID 为i 的锚点发送的跳数表见表1.

表1 锚点A(i)发送的跳数表Table 1 Hop table sended by anchor A(i)

1.2 非线性－跳数加权

如图2 所示，未知节点S(a)通过式(6)可以分别获得它到锚点A(p)、A(i)、A(j)间的估算距离，将其与锚点的坐标代入三边定位方程组:

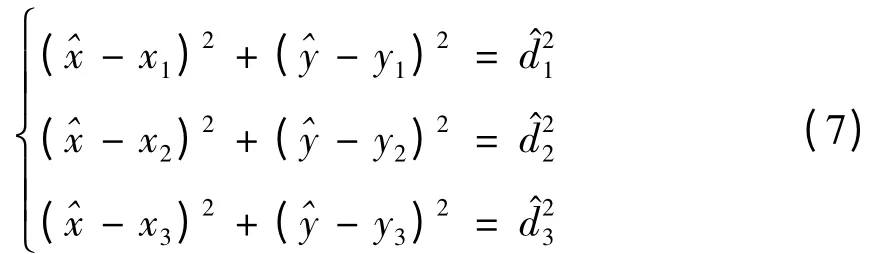
通过极大似然法可以求得基于锚点A(p)、A(i)、A(j)的S(a)的一个估计坐标(，).式(7)中的(x1，y1)、(x2，y2)、(x3，y3)分别为3 个锚点的坐标，1、2、3分别为未知节点与3 个锚点的估计距离.重复上述过程可得到S(a)在不同锚点下的所有估计坐标.通常将它们的平均值作为最终的估计坐标.但当S(a)选择图2 中的锚点A(i)、A(j)、A(k)时，由于它们基本上在同一条直线上，这时通过极大似然法求解，可得到图2 中S(a)关于直线L 对称的S(a')的坐标，这会对最终结果产生较大的影响.为此，文献［15］中提出了将3 个锚点间的角度作为非线性加权因素.另一方面，未知节点到这3 个锚点的跳数和越大，误差的累计效应越明显;对比S(a')与S(b')可知，未知节点到这3 个锚点的跳数之和在一定程度上能反映镜像坐标间的距离.显然，镜像坐标间的距离越大，误差越严重，故未知节点到3 个锚点间的跳数之和也可以作为该坐标加权的一个因素.

图2 镜像坐标示意图Fig.2 Schematic diagram of mirror coordinate

结合文献［15］的非线性加权，文中提出了“非线性－跳数”加权因子.未知节点μ 由ID 为x1、x2、x3的锚点所估算得到的坐标对应的权值可表示为

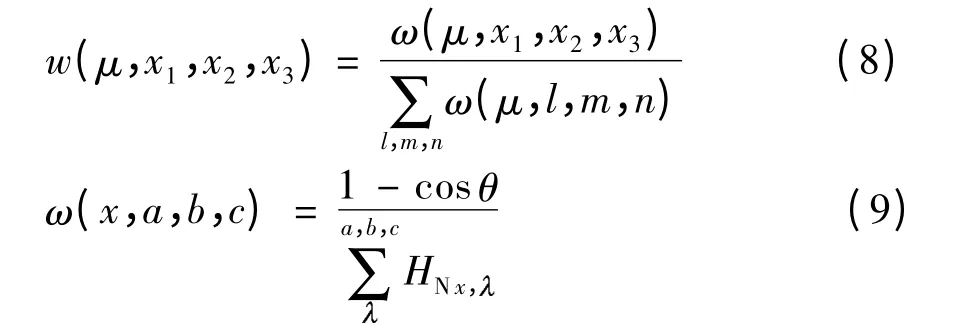
式中，θ 为由锚点A(a)、A(b)、A(c)组成的三角形的最小内角， 表示未知节点的ID，为未知节点S()到这3 个锚点的跳数之和.对于同一个未知节点，为所有加权值的总和，将该值作为分母，实际上是进行归一化处理.这样可使得所有“非线性－跳数”加权因子的总和为1.由前面分析可知，当3 个锚点连线近似呈直线时，容易产生镜像坐标，而此时由这3 个锚点组成的三角形的最小内角θ 相应减小，式(9)中加权因子的分子(1- cosθ)也减小，故对应坐标的权值变小，这样就能减小镜像坐标对最终估计坐标的影响.当θ 相同时，依据文献［12］，未知节点到锚点间的跳数越小，估距精度越准确，此时对应式(9)中的分母越小，相应权值越大，说明未知节点估计坐标的可信度与权值的变 化 一 致.若表 示 由 锚 点A(i)、A(j)、A(k)估算的坐标，则加权因子w(x，i，j，k)表征了该坐标的可信度.最终未知节点μ 的估计坐标可表示为

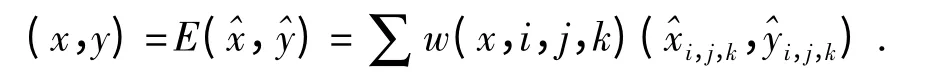
1.3 算法流程

文中提出的改进DV-Hop 算法流程如图3 所示.

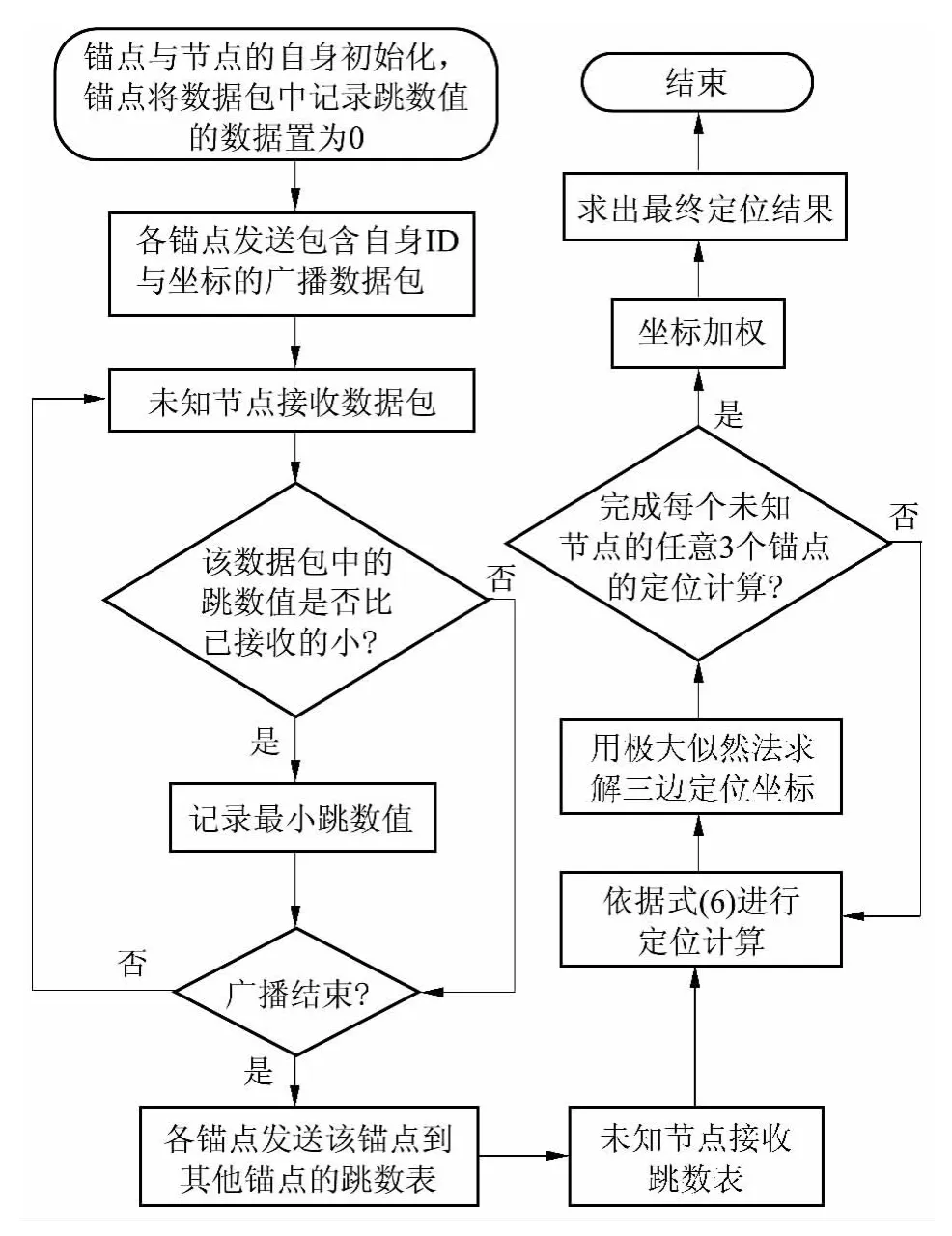
图3 改进DV-Hop 算法流程图Fig.3 Flowchart of modified DV-Hop algorithm

2 仿真实验分析

为验证文中算法的定位性能，以Matlab 2010b为仿真平台进行仿真实验，并选取边长为100 m 的二维平面正方形空间作为无线传感器网络的定位区域，未知节点完全随机分布在此区域中.未知节点和锚点的总数N、节点间的通信半径R、锚点数Na等依据不同的实验目的有不同的设置.参考文献［8，13］的计算方法，文中取绝对定位误差e 和归一化定位误差e 的计算公式如下:

式中，M 为实验次数，(xi，k，yi，k)和分别为第k 次分布下ID 为i 的节点的实际坐标和最终估计坐标.

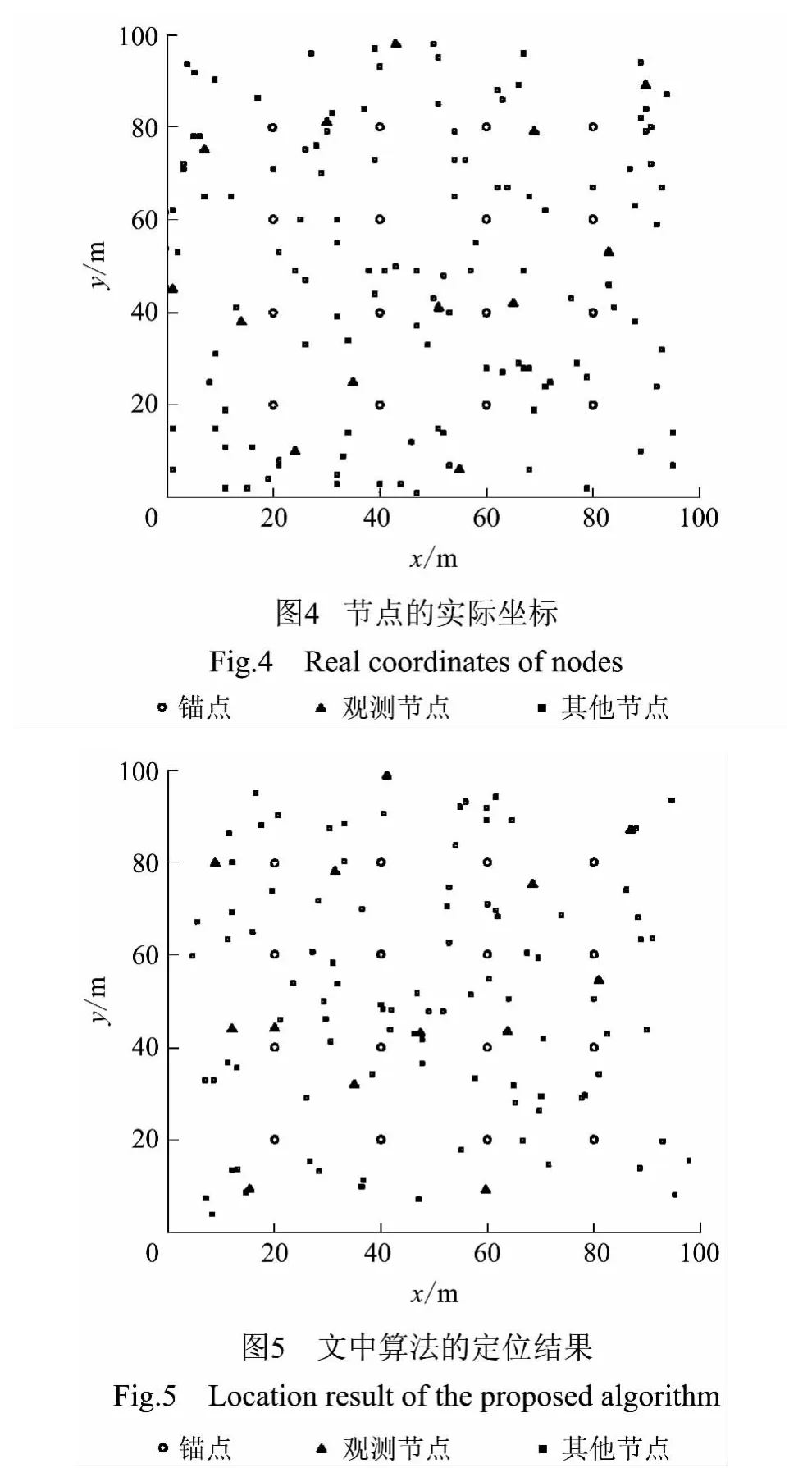
当N=150、Na=16、R=15 m 时节点的实际分布情况如图4 所示.使用文中算法进行定位计算，结果如图5 所示.对比图4、5 中随机选取的13 个未知节点(以▲表示)的位置，可以看出文中算法能够有效地实现传感器网络的定位.依据式(10)和(11)计算，得到绝对定位误差为4.8 m，归一化定位误差为0.32.

当R=15 m、N=150、K=50 时采用文中算法、文献［8］算法、DV-Hop 算法［10］及NDV-Hop 算法［6］进行实验.针对同一次节点分布情况，选取不同的锚点个数依次计算4 种算法的归一化定位误差.由于锚点分布对定位精度有一定的影响，因此本实验将锚点的分布分为等间隔理想分布和引入随机误差的理想分布.不同锚点数下4 种算法的归一化定位误差如图6 所示.从图中可以看出:随着锚点数的增加，归一化定位误差基本上呈下降趋势，文中算法的平均定位误差小于其他3 种算法;优化锚点分布可以提高定位精度.

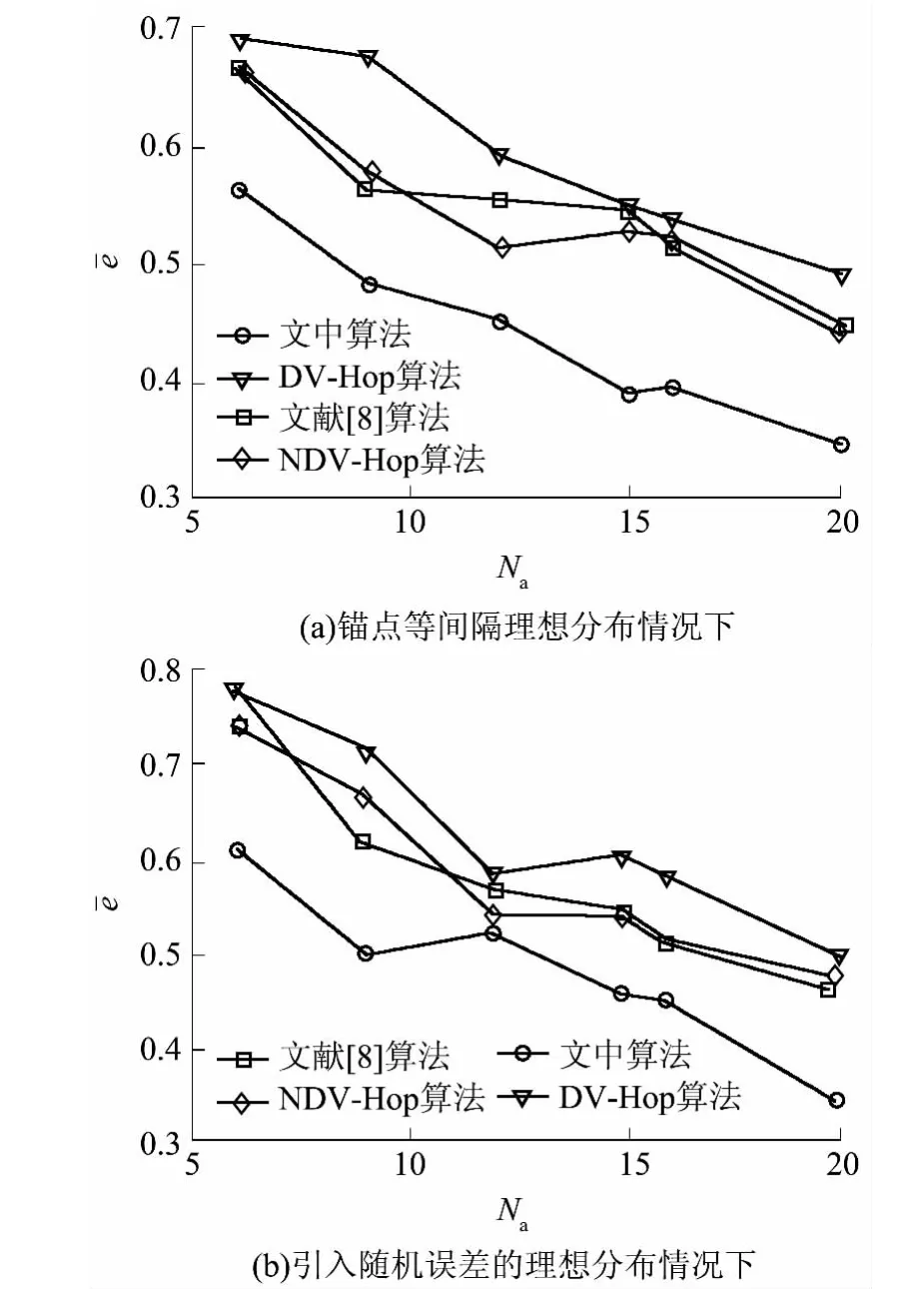
图6 锚点个数与归一化误差的关系Fig.6 Relationship between number of anchor and normalization error

当N=150、K=20 时不同通信半径下文中算法的绝对定位误差如图7 所示.从图中可以看出，绝对定位误差随通信半径的增大而上升，通信半径相同时，锚点数决定了定位精度.从理论上分析，随着通信半径的增大，节点间的跳数有所减少，平均每跳距离有所增大，估距的分辨率有所降低，因此定位误差有所增大，这和实验结果一致.但通信半径不能过小，通信半径与接收到锚点信息的未知节点所占比例δ的关系如图8 所示.从图中可以看出，当通信半径小于15 m 时，不能保证所有未知节点均能收到锚点的广播信息，这将导致无法定位某些未知节点.因此，在定位区域和锚节点数一定的条件下，选取通信半径是一个优化问题.对于本实验的分布模型，R=15 m可以认为是一个最优解.

当R=15 m、N=150、Na=16、K=10 时采用文中算法进行实验，在定位过程中，3 种估距方式所占的比例分别为29%、37%、34%，估距误差ed分别为0.18、0.22、0.31，其中ed的计算方法如下:

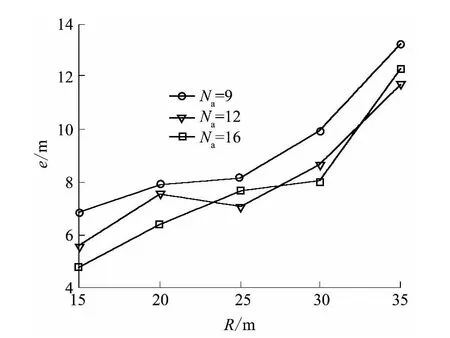
图7 通信半径对文中算法定位误差的影响Fig.7 Effect of communication radius on location error of the proposed algorithm

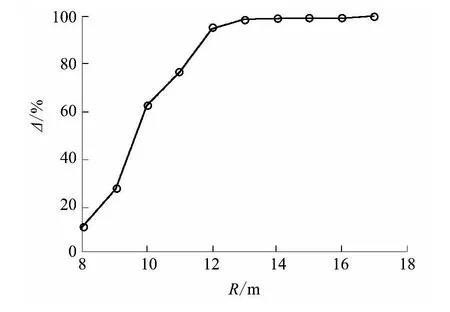
图8 通信半径与接收到锚点信息的未知节点数的关系Fig.8 Relationship between communication radius and number of unknown nodes received anchor information

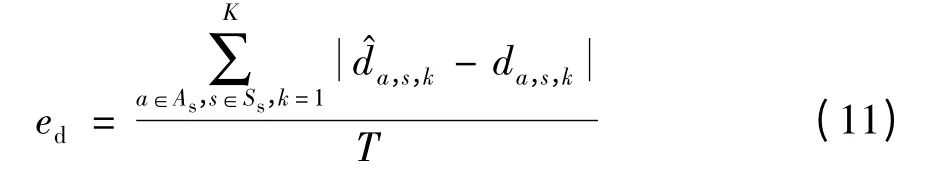
3 结语

通过分析DV-Hop 算法在估距时产生误差的原因，文中提出了基于估距方式分类的无线传感器网络定位算法，并结合“非线性－跳数”加权因子进一步减小估距误差，最后通过Matlab 仿真验证了文中算法的定位性能.随着锚点数的增加，定位所需的通信开销和计算量将大幅增加.如何在保证定位精度的同时减少通信量和计算量，将是今后研究的重点.

［1］Li Shiwei，Yang Guoyan.Introduction to wireless sensor network node location algorithms and multi-path robustness［C］∥Proceedings of the 7th International Conference on Information Technology and Application.Sydney:ICITA，2011:102-104.

［2］Guo Jianquan，Zhao Wei.An anchor free location algorithm for large scale wireless sensor networks［C］∥Proceedings of 2008 IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications.Beijing:IEEE，2008:7-12.

［3］Kumar Shrawan，Lobiyal D K.An advanced DV-Hop localization algorithm for wireless sensor networks ［J］.Wireless Personal Communications，2013，71(2):1365-1385.

［4］Wu Chengdong，Chen Shifeng，Zhang Yunzhou，et al.A RSSI-based probabilistic distribution localization algorithm for wireless sensor network［C］∥Proceedings of the 6th IEEE Joint International Conference on Information Technology and Artificial Intelligence.Chongqing:IEEE，2011:333-337.

［5］张爱清，叶新荣，胡海峰，等.基于RSSI 每跳分级和跳距修正的DV-HOP 改进算法［J］.仪器仪表学报，2012，33(11):2552-2559.Zhang Ai-qing，Ye Xin-rong，Hu Hai-feng，et al.Improved DV-HOP positioning algorithm based on one-hop subdivision and average hopping distance modification［J］.Chinese Journal of Scientific Instrument，2012，33 (11):2552-2559.

［6］Liu Jicheng，Wang Wenxiu，Shang Yintong.An improved localization algorithm for wireless sensor network based on DV-Hop［C］∥Proceedings of 2012 International Conference on Measurement，Information and Control.Harbin:IEEE，2012:511-515.

［7］Lu Qingling，Bai Mengliang，Zhang Wei.A new kind of NDV-Hop algorithm in wireless sensor network ［C］∥Proceedings of 2011 International Conference on Network Computing and Information Security.Guilin:IEEE，2011:438-441.

［8］刘峰，张翰，杨骥.一种基于加权处理的无线传感器网络平均跳距离估计算法［J］.电子与信息学报，2008，30(5):1222-1225.Liu Feng，Zhang Han，Yang Yi.An average one-hop distance estimation algorithm based on weighted disposal in wireless sensor networks［J］.Journal of Electronics and Information Technology，2008，30(5):1222-1225.

［9］Zheng Yousi，Wan Lei，Sun Zhi.A long range DV-Hop localization algorithm with placement strategy in wireless sensor networks ［C］∥Proceedings of the 4th International Conference on Wireless Communications Networking and Mobile Computing.Avignon:IEEE，2008:4090-4094.

［10］吴玉成，李江雯.基于最优节点通信半径的改进DVHop 定位算法［J］.华南理工大学学报:自然科学版，2012，40(6):36-42.Wu Yu-cheng，Li Jiang-wen.Improved DV-Hop localization algorithm based on optimal communication radius of nodes［J］.Journal of South China University of Technology:Natural Science Edition，2012，40(6):36-42.

［11］Li Bing，He Yigang，Guo Fengming，et al.A novel localization algorithm based on isomap and partial least squares for wireless sensor networks ［J］.Instrumentation and Measurement，2013，62(2):304-314.

［12］XiaoQingjun，Xiao Bin，Cao Jiannong，et al.Multihop range-free localization in anisotropic wireless sensor networks:a pattern-driven scheme［J］.IEEE Transactions on Mobile Computing，2010，9(11):1592-1607.

［13］朱敏，刘昊霖，张志宏，等.一种基于DV-Hop 改进的无线传感器网络定位算法［J］.四川大学学报:工程科学版，2012，44(1):93-98.Zhu Min，Liu Hao-lin，Zhang Zhi-hong，et al.An improved localization algorithm based on DV-Hop in WSN［J］.Journal of Sichuan University:Engineering Science Edition，2012，44(1):93-98.

［14］Yao Ge，Zhang Jie，Yao Sufen.Research of node location algorithm in wireless sensor network ［J］.Advances in Intelligent and Soft Computing，2011，129(2):309-313.

［15］Xiang Shu，Zhang Yun-zhou，Xia Zhi-jia，et al.An improved DV-Hop localization algorithm using residual weight in wireless sensor network［J］.Journal of Computational Information Systems，2012，8(15):6357-6364.

［16］Tan Lixiong，Luo Fei，Liu Kai.Weighted centroid location algorithm in wireless sensor network［C］∥Proceedings of IET International Communication Conference on Wireless Mobile and Computing.Shanghai:IEEE，2011:414-418.