用于信号盲提取的最大三阶相关峭度反卷积算法*

杨光永 胡国清 陈乐 吴海锋 宋佳声

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640;2.云南民族大学 无线传感器网络云南省高校重点实验室，云南 昆明 650031)

采用半导体激光源和线阵电荷耦合器件(CCD)图像传感器并以激光三角法测量物体的位移时，物体的位移、厚度、透明度、表面粗糙度、介质吸收系数、折射系数和光点直径等因素综合作用于线阵CCD 图像传感器，使激光位移测量系统(LDMS)的模拟前端(AFE)输出多种混合信号，包括激光位移信号、多重反射位移信号、高斯白噪声、瑞利散射噪声等［1］.

LDMS 信号处理的主要任务是对AFE 的混合信号进行解混合处理，抑制或消除高阶和低阶统计噪声，以提取或恢复激光位移信号分量或多重反射信号.常规的信号处理方法可分为两类:①采用自适应滤波器，将LDMS 当作线性多输入多输出系统，AFE及所有光路传输通道特性都是内部透明的，按信号的低阶统计特性和参考模型设计自适应滤波器，如有限元离散化模型滤波器(FEM-FIR)［2］，采用图像传感器布局优化设计的阵列CCD 传感器［3］，两帧位移图像的相移干涉检索方法［4］，反射散斑干涉全息图像法［5］.该类方法将幅值最大的点或尖峰脉冲序列的对称中心点当作激光位移信号的采样序列点，以低阶统计量或二阶相关峭度描述激光位移信号或多重反射信号的特性，信噪比较低，但难以滤除混合信号的超高斯噪声或亚高斯噪声，且很难准确获取系统的参考模型.②将测量系统看作时不变的、信号与各种噪声分量相互独立的盲系统或部分特性已知的半盲系统，采用最大熵［6-7］、自然梯度法［8］、神经网络［9］、独立分量分析方法［10］和盲自适应滤波［11］等盲源信号分离方法，对机械故障诊断［12-13］、雷达及声纳的目标探测［14］、地层反射探测［15］、医疗图像分析［16］等进行盲信号提取，对LDMS 及其相关盲信号提取的研究鲜见报道.特别地，在微位移测量条件下，混合信号的均方误差趋于0 或偏态较大，基于最大熵或自然梯度的盲源分离方法的收敛速度急剧降低.

激光位移信号和多重反射信号的采样序列分布在AFE 输出混合信号中峰态不为0、峭度和峭度梯度同时达到最大值的尖峰脉冲序列区间，文中将CCD 传感器像元的选择性、激光光点和光路系统当作部分特性和结构已知的LDMS 半盲系统(信号分量与噪声相对独立)，提出了最大三阶相关峭度反卷积算法(M3CKD):以三阶相关峭度(M3CK)度量激光位移信号或多重反射信号的统计特性，当M3CK 达到最大值时盲提取信号，反卷积滤波器输出激光位移信号和多重反射信号;并通过实验验证了该算法的有效性.

1 反卷积逆滤波器及信号提取

设由线阵CCD 传感器、模拟前端构成时不变的线性系统，传感器源信号矢量s(k)Rn之间独立同分布，n(k)Rn是均值为0 的加性噪声过程，对混合模型进行卷积运算后获得观测矢量x(k)Rm，记2 范数为，且xi(k)≥0，则

在最大值条件下，获得逆滤波器Wp(k)的迭代最优解，解混合系统，抑制噪声分量，从而盲提取激光位移的源信号s(k):

得到反卷积输出的一般形式为

2 最大三阶相关峭度反卷积算法

2.1 逆滤波器

为了获得逆滤波器Wp(k)的迭代解，令

先对式(2)的分子进行微分，得

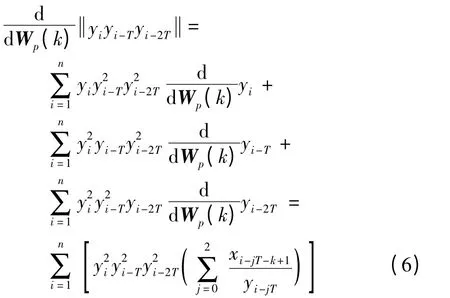
再对式(2)的分母进行微分，得

结合式(6)和(7)，解方程(5)得

2.2 算法的收敛性分析

为了考察三阶相关峭度反卷积算法的收敛性，设yi+1=yi+δyi，δ(0≤δ＜1)为增量因子，将Kc，i+1(T)在yi处按泰勒级数展开，得到

式(2)对yi进行微分，得

整理式(11)，得

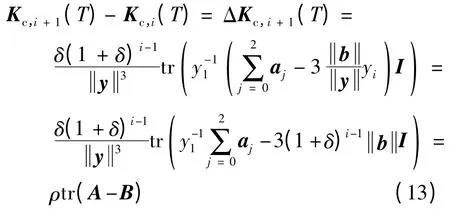
则tr(A -B)＞0 ，ΔKc，i+1(T)＞0 ，盲反卷积滤波器输出的三阶相关峭度单调增加，经有限次迭代之后，满足迭代终止条件:

此时，峭度反卷积算法收敛，收敛速度由系数ρ 和A-B的迹联合决定.

2.3 算法的稳定性分析

由前面的分析可知，当式(13)的A -B 为非奇异、所有特征值 i＞0(i= 1，2，…，n)时，最大三阶相关峭度算法收敛.再次考察A-B 的迹，可得

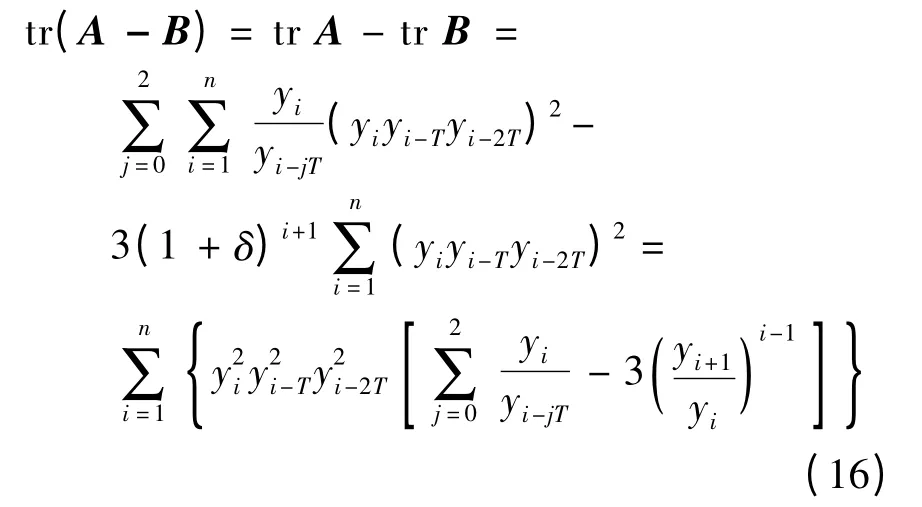
因此，算法稳定的必要条件是

周期为T 的观测序列中，满足式(17)的激光位移信号和多重反射信号被盲提取.

3 实验与结果分析

首先用模拟数据进行仿真以验证文中算法的性能，再利用激光位移测量系统的模拟前端输出数据进行实验，并与FastICA 算法的实验结果进行对比分析.

3.1 模拟数据仿真

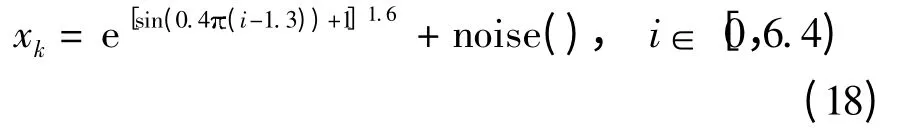
位移量或多重反射位移量并非处于信号的峰值点，而是处于信号的中心点距原点的偏移量.本实验中，设计6 帧观测序列，每帧包含1 024 个点，其中64 个位移量数据分布在中心为D 的范围内，

D= [ 432 432 432 950 50 512 ].

设线阵CCD 图像传感器的像素点间距为q，则仿真的第1 帧激光位移量d01=432q.同理，设第1 帧的第1 和第2 重反射信号的位移量距中心D 的偏移量分别对应ΔD 的第1、第2 行向量，即

可得第1 帧的第1 重反射位移d11= -120q，第1 帧的第2 重反射位移d21=-300q.

图1 线阵CCD 图像传感器的模拟信号Fig.1 Simulated signals of linear CCD image sensor

实验中设文中算法的迭代次数为15，FIR 滤波器的单位抽样数为50，采样周期T=5，分别输入各帧数据，仿真结果如图2 所示.其中，FastICA 的版本为V2.5，终止迭代条件ε=10-4，最大迭代次数为100.从图可以看出观测序列的噪声功率与算法的收敛速度有关:噪声功率越大，峭度突变信息和越大，相关峭度的梯度值越大(如第1 和第4 帧曲线)，文中算法迭代5 次后接近迭代终止条件ΔKc，i+1(k)＜0.001，收敛速度越快，而同等条件下的FastICA 算法需要迭代9 次.当进行微位移测量时，FastICA 算法的收敛速度和信噪比急剧降低，由此可以看出M3CKD 算法在高精度微位移信号测量中的优势.

图2 M3CKD 和FastICA 算法的仿真结果Fig.2 Simulation results of M3CKD and FastICA algorithms

对于不同噪声功率和信噪比条件下的6 帧模拟数据，在10 次迭代之后，M3CKD 和FastICA 算法均能达到收敛终止条件，但M3CKD 算法的收敛速度更快，信噪比更高，且无需白化处理.

3.2 激光位移测量实验

利用量块、X/Y 伺服工作台、传感器及模拟前端、数据处理及控制器构成激光位移实时测量系统(如图3 所示)，以KEYENCE 公司的LK-H055 和LK-G5001V 构成标定系统进行线性度误差测量实验.

图3 激光位移测量和标定系统Fig.3 Laser displacement measurement and calibration system

以步长为1 mm、-5 mm 为原点，在±5 mm 正反行程范围内采集测量位移ym(i)和标定位移yc(i)，获得三阶相关峭度梯度误差ei:

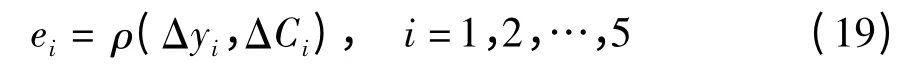
式中:ρ(，)为三阶相关峭度的自然梯度函数;Δyi为标定误差，Δyi=ym(i)-yc(i);ΔCi为峭度微分.对三阶相关峭度梯度误差线性进行多项式拟合，以考查系统的线性度，其结果如图4 所示.

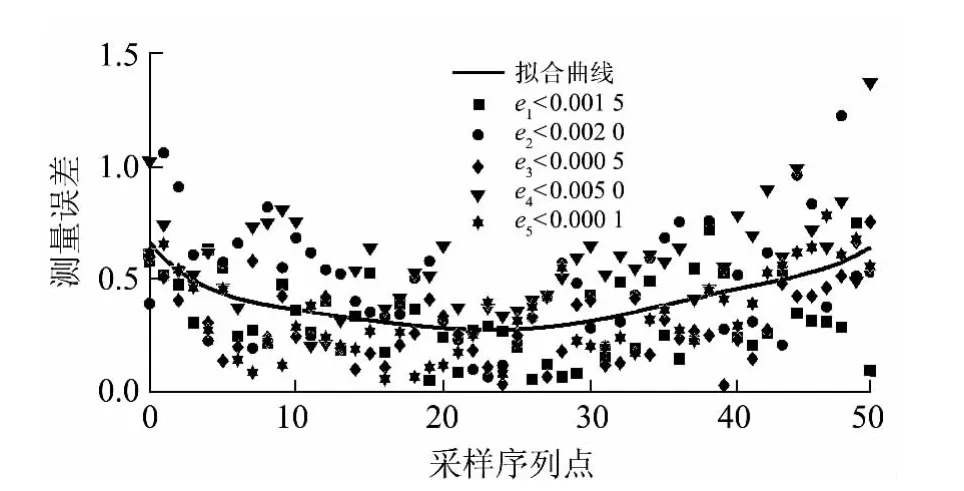
图4 不同峭度梯度误差条件下的测量误差Fig.4 Measuring errors under different kurtosis gradient errors

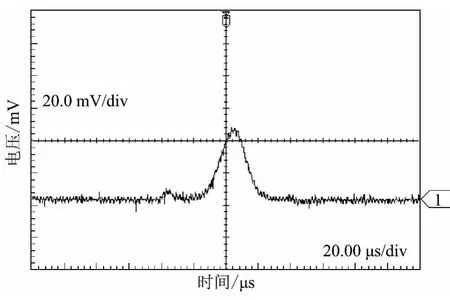
图5 PVC 样品的位移测量结果Fig.5 Measuring result of displacement for PVC sample

从图4 可以看出三阶相关峭度梯度误差与测量误差的关系.偏离测量范围的中点越远，线性度误差越大，这反映了LDMS 的结构特性.标定位移为5000 μm、标称厚度为20.0 μm 的聚氯乙烯(PVC)样品的位移测量实验结果如图5 所示(CCD 传感器的像素点间距为3 μm).

设反卷积输出序列的最大值对应的采样序列点为k0，滞后p 个采样序列(除两端点之外，p=3)，则激光位移量为3(k0-p)，单位为μm.从图5 可以看出，多重反射信号峰值与位移信号峰值的采样序列点k0≈9.5，可得该实验条件下的厚度测量误差为(9.5-3.0)×3 -20= -0.5 μm.

4 结语

文中提出了最大三阶相关峭度反卷积算法，用以实现激光位移信号和多重反射信号的盲提取，该算法具有较快的收敛速度、稳定性和较高的信噪比.但文中的仿真和误差测量实验均是在既定系统体系结构下完成的，当模拟前端的激光光点直径变化、CCD 传感器的相移时钟变化、通过更换滤光片或微调透镜组等使系统的体系结构变化时，依照经验值调节M3CKD 算法的采样周期、迭代终止条件，计算效率将较低.今后拟采用加权三阶相关峭度来度量激光位移信号和多重反射信号的高阶统计特性，以改进M3CKD 算法的自适应能力.

［1］Soler F J P.Multiple reflections in an approximately parallel plate ［J］.Optics Communications，1997，139(4):165-169.

［2］Hong Yun Hwa，Lee Se Gun，Lee Hae Sung.Design of the FEM-FIR filter for displacement reconstruction using accelerations and displacements measured at different sampling rates ［J］.Mechanical Systems and Signal Processing，2013，38(2):460-481.

［3］Shiou Fang-Jung，Liu Min-Xin.Development of a novel scattered triangulation laser probe with six linear chargecoupled devices (CCDs)［J］.Optics and Lasers in Engineering，2009，47(1):7-18.

［4］Muravsky L I，Ostash O P，Kmet' A B，et al.Two-frame phase-shifting interferometry for retrieval of smooth surface and its displacements［J］.Optics and Lasers in Engineering，2011，49(3):305-312.

［5］Sainov V，Baldjiev A，Stoykova E.Full field displacement measurement by double symmetrical illumination with diode lasers through a pair of double exposure reflection holograms［J］.Optics and Lasers in Engineering，2013，51(6):656-664.

［6］Pinchas M，Bobrovsky B Z.A maximum entropy approach for blind deconvolution［J］.Signal Processing，2006，86(10):2913-2931.

［7］Cardoso J-F.Blind signal separation:statistical principles［J］.Proceedings of the IEEE，1998，86(10):2009-2025.

［8］Amari S，Douglas S C，Cichocki A.Multichannel blind deconvolution and source separation using the natural gradient［M］.Signal Processing Advances in Wireless Communications.Paris:IEEE，1997:101-104.

［9］Amari S I，Cichocki A.Adaptive blind signal processingneural network approaches［J］.Proceedings of the IEEE，1998，86(10):2026-2048.

［10］Hyvärinen Aapo，Karhunen Juha，Erkki Oja.Independent component analysis［M］.New York:John Wiley ＆Sons，2001:147-273.

［11］Radenkovic M S，Bose T，Ramkumar B.Blind adaptive equalization of MIMO systems:new recursive algorithms and convergence analysis ［J］.IEEE Transactions on Circuits and Systems Part I:Regular Papers，2010，57(7):1475-1488.

［12］McDonald Geoff L，Zhao Qing，Zuo Ming J.Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection［J］.Mechanical Systems and Signal Processing，2012，33(6):237-255.

［13］Endo H，Randall R B.Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter ［J］.Mechanical Systems and Signal Processing，2007，21(2):906-919.

［14］Liu Kefei，da Costa João Paulo C L，So Hing Cheung，et al.Subspace techniques for multidimensional model order selection in colored noise ［J］.Signal Processing，2013，93(7):1976-1987.

［15］Wiggins R A.Minimum entropy deconvolution［J］.Geoexploration，1978，16(1):21-35.

［16］蔡坤，谢胜利.基于高阶统计量的μ 节律脑电信号盲提取［J］.华南理工大学报:自然科学版，2011，39(5):12-17.Cai Kun，Xie Sheng-li.Blind extraction of μ-rhythm electroencephalogram signals based on high-order statistics［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(5):12-17.