基于复合滑移的微纳缝隙剪切流研究*

陈晖 沈明

(1.福州大学 机械工程及自动化学院，福建 福州 350108;2.福州大学 数学与计算机科学学院，福建 福州 350108)

微缝隙流动广泛存在于流体动力系统、微纳机电系统、薄膜流体润滑和高端集成电路(IC)装备［1］等领域中，在压力和流量等参数的控制方面发挥着重要作用［2-3］.当液膜缝隙厚度为微纳尺度时，表面效应愈加明显，其内部流动规律将明显区别于宏观流体流动，其中一个突出的特征是液固交界处的边界滑移［4］.

实验显示微纳尺度下滑移长度从几纳米到几十微米不等，边界滑移对流动特性的影响显著［5-6］.边界滑移受到众多因素的影响，其中一个关键参数是界面的亲疏液性质.在超疏液界面下，固体表面分子与液体分子间的吸引力很容易被流体流动所带来的剪切率平衡，易在固体表面形成速度滑移［7］;其主要原因是在疏液固体表面存在微纳气层，液体在其上面实现近自由剪切流动;通过界面微纳结构设计，提升固液界面的微气体比例，则可实现大尺度的滑移［8］.对于亲液性界面，由于其表面较强的残余化学键，表现出高的表面能，对流体分子具有较强的吸附力，一般很难产生滑移，甚至会产生抑制液体流动的负滑移现象［9-11］.

滑移流动目前仍未有一个公认的物理机制和模型［12-14］，对于它的研究常伴随着新现象和新规律的发现，尤其是在亲液和疏液复合界面下的微流动研究中.如通过对纳米水膜的试验研究发现，当水膜位于亲水壁面和疏水壁面之间时，即便下方疏水壁面运动速度非常快，上方亲水壁面对水膜仍有着非常强且稳定的束缚，这是一个有趣的现象［15］.

文中围绕着微纳尺度下典型的平板缝隙剪切流，建立基于Navier 滑移的二维微流动精确解模型，在此基础上结合文献中试验测量所得的滑移参数值，研究亲液和疏液复合界面内的瞬态滑移流动行为，以及壁面性质对微缝隙流动的作用规律.

1 数学模型

1.1 微缝隙剪切流的控制方程与边界条件

微缝隙流动主要受到进出口压差和壁面剪切作用，对于主要为层流的微纳流动，在此基础上将形成相互独立的压差流和剪切流.

压差流充分发展后的流动速度场呈抛物线分布，流动形式稳定.剪切流动受壁面运动影响强烈，并伴随时间发生瞬时变化，因此研究瞬态剪切滑移流动对全面获知微缝隙的内部流动规律十分必要.

设缝隙微流动为层流且不可压缩，忽略进出口压差和重力的影响，则二维微缝隙流动的控制方程为

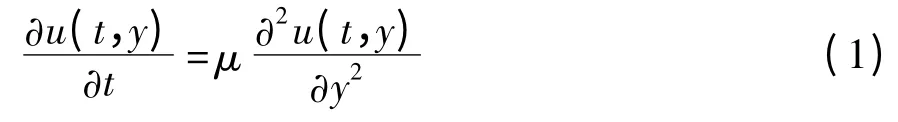
式中，u 为液体的流动速度，μ 为液体的动力黏度，t为微缝隙壁面的运动时间，y 为液体质点与缝隙下壁面的距离.

由式(1)可知，除液体性质μ 和微缝隙厚度h之外，微缝隙流动的速度u 还受到壁面运动状态及性质的影响.

由于微缝隙流动的壁面剪切率普遍低且沿壁面分布处处相等，与粘性剪应率和滑移系数成正比的Navier 滑移模型［16］在该状态下模型简单可靠，因此采用该模型描述界面滑移现象，其基本形式为

式中:W 为壁面边界;b 为滑移长度，该值反映壁面材料属性并由试验测定.

壁面亲疏液性质对于滑移的影响主要通过滑移长度b 的大小描述.滑移长度为正且其值大意味着液固界面的滑移强度大;滑移长度若为负值(即负滑移)则表明在距离该壁面一定范围内存在静止的液体层.

基于Navier 滑移模型的微缝隙剪切流原理如图1 所示.以静止上壁面处的滑移流动为例，假设无滑移速度位于离实际固壁上方距离为b2的位置(即该处的速度u'为零)，同时认为上壁面处的液体流速与当地局部应变率成正比，由此描述壁面处具有一定流动速度u(t，h)的滑移现象，而经典无滑移认为该位置的液体速度为零.定义下壁面运动速度V 的最大值为U，在Navier 滑移模型中，在距离运动壁面下方b1的位置处的速度u'等于壁面最大运动速度U.

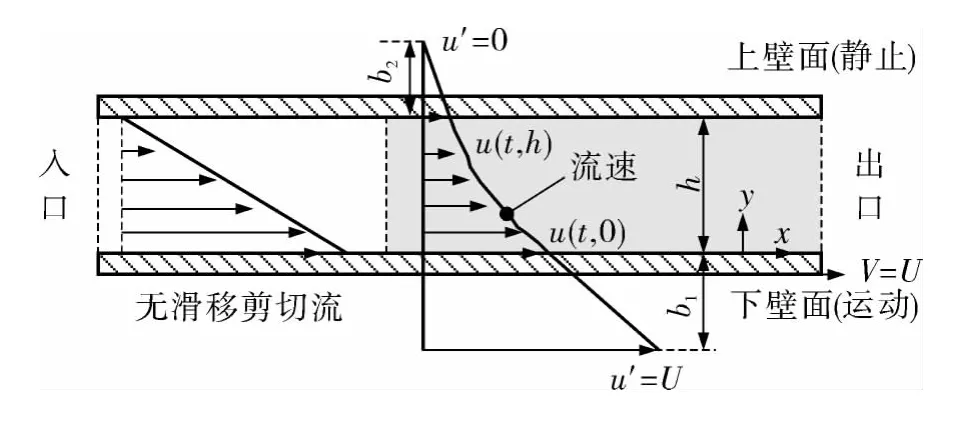
图1 基于Navier 滑移的缝隙流模型Fig.1 Gap-flow model with Navier slip condition

为研究壁面性质对微流动的影响规律，基于Navier 滑移模型建立微缝隙剪切滑移流动的初边界条件:

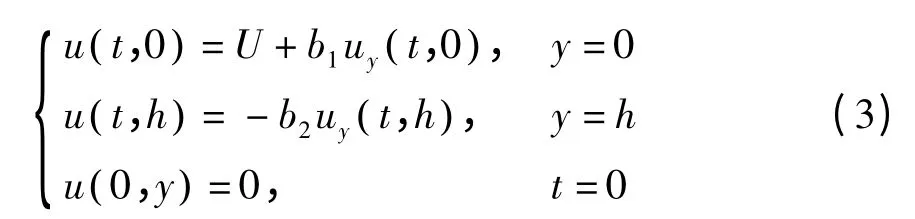
式中，b1为下壁面的滑移长度，b2为上壁面的滑移长度，h 为微缝隙的厚度.

1.2 剪切微流动的精确解建模

由于初边界问题(1)和(3)具有非齐次的第3类边界条件，直接求解十分困难.为将其转化为齐次边界求解，令

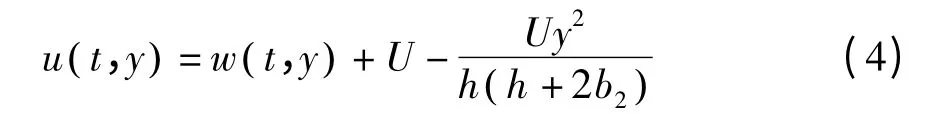
将方程(4)代入初边界问题(1)和(3)得

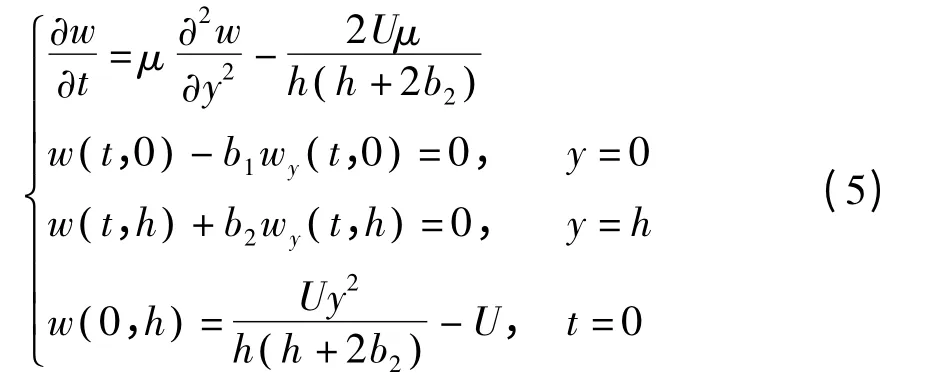
利用叠加原理，将方程(5)分解为

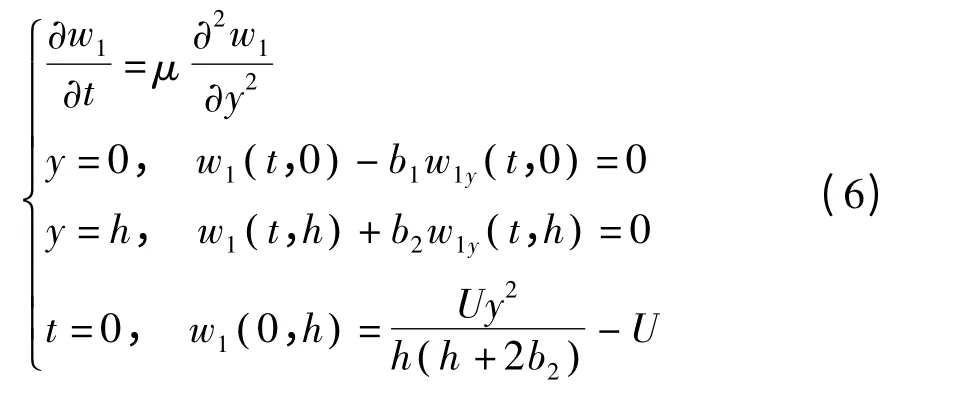
和

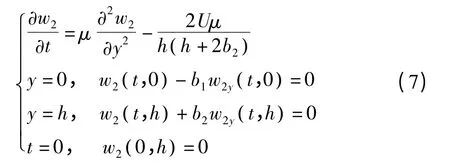
并且有

利用分离变量法和齐次化原理，求得w1和w2.结合方程(4)和(8)，得复合滑移下的微缝隙速度场的精确解为

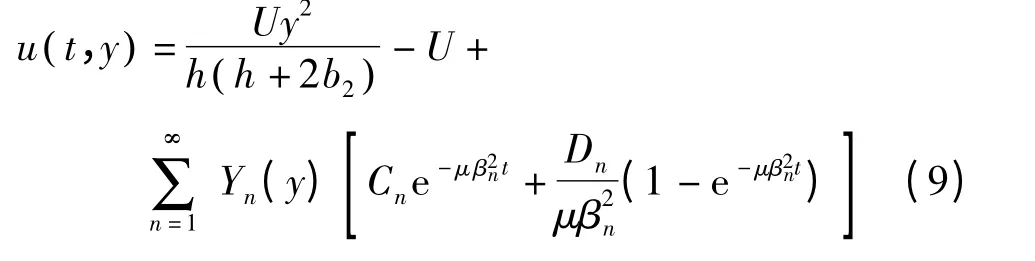
其中，

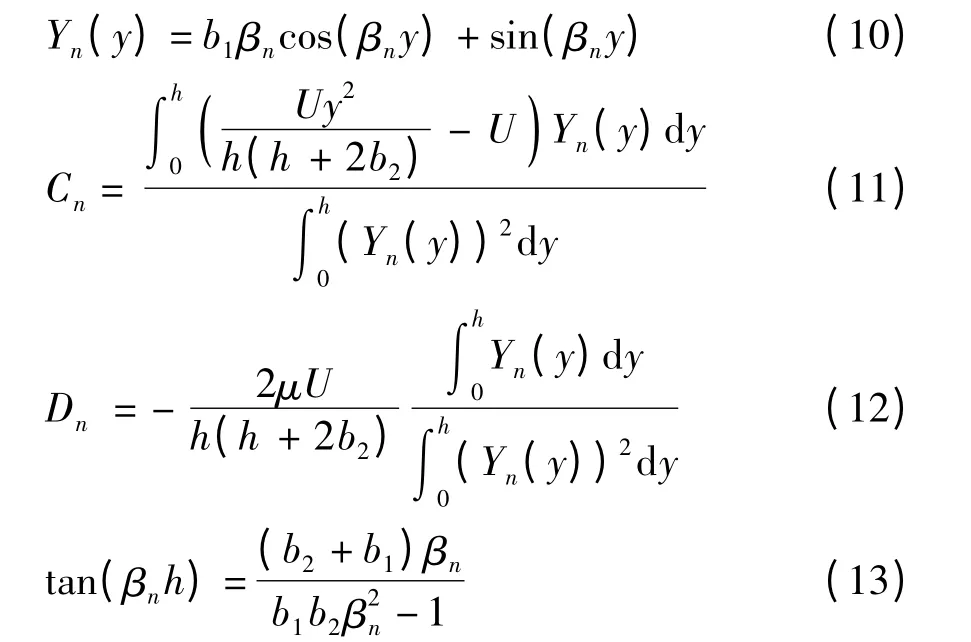
式中，βn(n=1，2，3，…)为式(13)的可列无穷多个正解，利用数值求解法可得其满足βn＜βn+1.

根据方程的解(9)－(13)和级数理论可知u(t，y)是收敛的.n=500 时的u(t，y)比n=499 的增量小于10－8，结果变化微小，可近似认为解已收敛.因此，文中取n=500 进行求解分析.

2 结果与分析

试验显示不同疏液性表面的滑移长度差异大.Tretheway 等［17］采用Micro-PIV 对特征尺寸为30 μm的流动系统进行测定，所得滑移长度约为1 μm;Chang 等［6］利用流变仪测定端面间隙为53 μm 的系统，以水为介质时的最大滑移长度为20 μm.因此，文中的滑移长度b1、b2选取为缝隙厚度h 的正负0.01～0.30 倍.

区别于疏液表面的正滑移，亲液性表面由于液体分子吸附力而呈现出负滑移现象，但滑移长度仅为几纳米［9］.因此，所分析具有亲液壁面的微缝隙厚度取纳米级.此外，为便于分析，取纯水为液体介质，缝隙运动壁面的速度为0.5 m/s，流场厚度h 为10～105nm，滑移长度b1、b2取±(0.01h～0.30h)，壁面运动速度V 为0.5 m/s，时间t 为0.0～0.1 s.

2.1 模型的可靠性验证

为验证数学模型的可靠性，基于Fluent 软件建立二维非定常计算流体动力学模型(CFD)进行对比分析.在CFD 模型中，将入口和出口处网格进行链接并建立周期性边界条件，由此消除进出口压差带来的影响;在此基础上，编写基于Navier 滑移的udf程序组，将其作为边界条件分别加载到微缝隙流场的上下壁面中.此外，设置缝隙厚度方向的网格为100 层，以更加准确地获取微缝隙的滑移流动规律.

在典型流场厚度(h=100 μm)和两壁面具有相同滑移强度(滑移长度均为b1=b2=0.1h)的状态下，伴随下壁面以V=0.5 m/s 的速度运动，缝隙中心流场(y=0.5h)的流速变化规律如图2 所示.图中，u(t，0.5h)/V 为流场中心的无量纲液体流速.

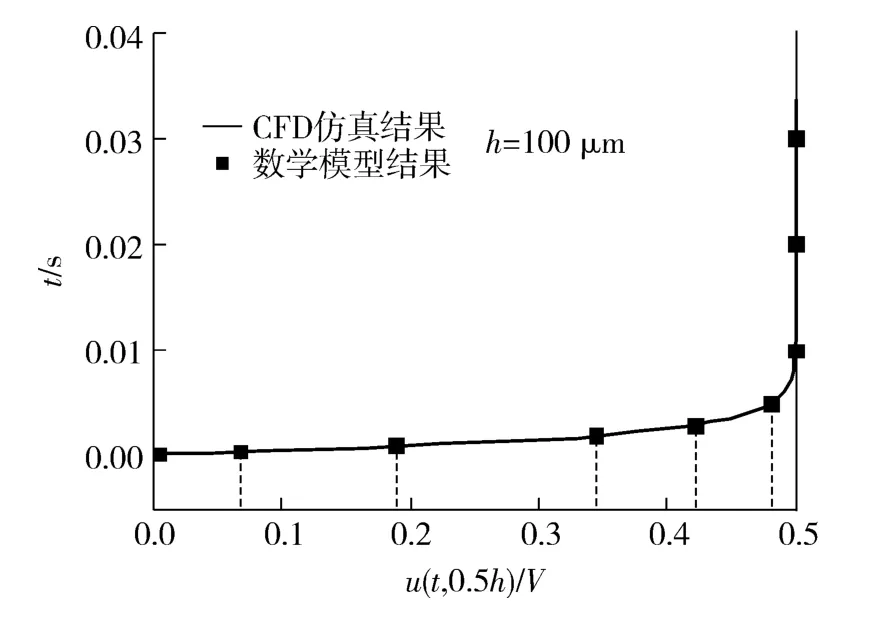
图2 CFD 仿真与数学模型的瞬态结果对比Fig.2 Comparison of unsteady results of CFD simulation and mathematical model

结果显示，CFD 仿真与数学模型的计算结果一致.伴随下壁面的运动，粘性牵拉作用使中心流场的速度迅速提升并趋向于恒定值，这种现象在无滑移剪切流中同样存在［15］.上下壁面的滑移强度一致导致两壁面的滑移作用相互抵消，使中心流场的稳定流速u(t，0.5h)等于壁面运动速度V 的一半.

值得注意的是，在这种缝隙较大情况下，流速稳定的过程仍然迅速(＜0.01 s).对于尺度更小的微纳缝隙，壁面运动影响的增强将使流速稳定时间进一步缩短.因此，为便于研究，后面主要围绕稳定状态(取壁面运动时间为0.1 s)利用该精确解模型研究微尺度下的滑移流动规律.

2.2 亲疏液复合滑移的微流动特性

界面滑移主要分为疏液正滑移和亲液负滑移两种类型，当微缝隙中同时存在亲液壁面和疏液壁面时，流动更加复杂.由于亲液负滑移的作用范围为纳米尺度，所以该问题的研究对象取厚度为10 nm 的微缝隙.

对于下壁面为疏液正滑移(b1＞0)、上壁面为亲液负滑移(b2＜0)的工况，其液体流速和水分子分布状态如图3 所示.图中，u/V 为无量纲的液体流速，y/h 为液体质点与下壁面的无量纲距离.亲液上壁面因负滑移作用形成具有与上壁面同处于静止状态的液体止滞层.在疏液下壁面运动状态下，增大上壁面负滑移长度将明显放大止滞层的厚度，当下壁面为疏液正滑移时这种效应将进一步增强，因此使微缝隙中部以上的液体均处于静止状态.

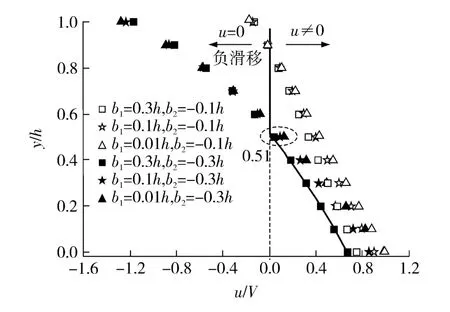
图3 下疏上亲型微缝隙的典型流速分布Fig.3 Typical velocity distribution of micro-gap flow with hydrophilic bottom-wall and hydrophobic upper-wall

由此可见，亲液上壁面将呈现出对微液体的强附着力，若进一步实现微缝隙的超亲液和超疏液壁面复合，则在边界快速运动下仍可有效束缚液体，这与试验发现在纳米亲疏水运动壁面中存在液体强束缚力的现象［15］相吻合.

从图3 中还可以看到，在同类壁面性质下，微缝隙流场呈近似线性分布.这说明壁面运动引起的微缝隙粘性剪切流达了到牛顿粘性定律的稳定状态，即线性流场分布.相比无滑移状态时呈45°斜率的稳定流速分布(即Couette 流)，该状态近运动壁面的流速变化更迅速.

对具有相反滑移性质的流场，即下壁面为亲液负滑移、上壁面为疏液正滑移的情况，典型结果如图4所示.

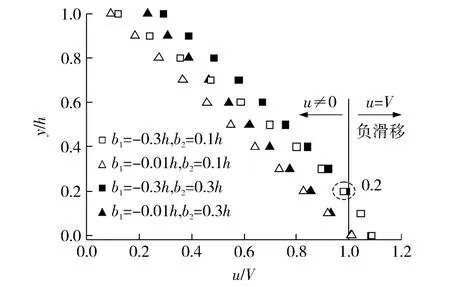
图4 下亲上疏型微缝隙的典型流速分布Fig.4 Typical velocity distribution of micro-gap flow with hydrophobic bottom-wall and hydrophilic upper-wall

相比较于前者，在相同滑移长度下，疏液壁面的滑移速度近似相等，但下壁面亲液负滑移时液体的止滞层厚度缩小60%，液固界面对液体的束缚力明显减弱.究其原理，主要是由于壁面运动增强了壁面及附近液体分子间的粘性剪切作用，从而削弱了液固界面对水分子的吸引力，由此降低了负滑移带来的影响.

2.3 变强度复合滑移的微流动特性

相同滑移类型、不同滑移强度是复合滑移界面的另一种典型形式.对于上下均为亲液型壁面的复合滑移，其典型微流动如图5 所示.

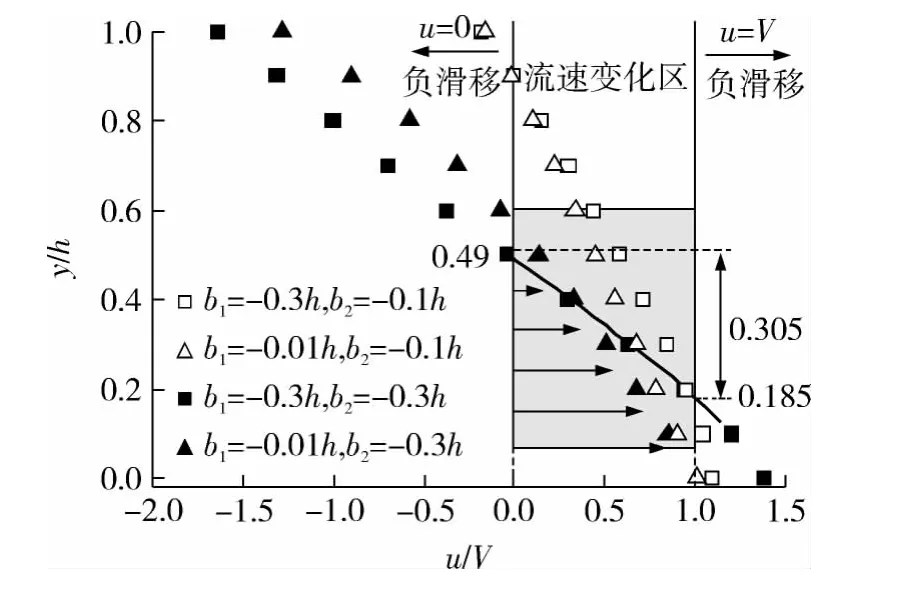
图5 亲液复合型微缝隙的典型流速分布Fig.5 Typical velocity distribution of micro-gap flow with complicated hydrophilic walls

流场内部存在两个负滑移区域，其内的液体相对壁面静止.增大滑移长度时，上壁面处液体的止滞区明显.对比图中3 中的亲疏液复合滑移，该类型下壁面的负滑移使运动壁面影响获得增强，从而导致微缝隙上方的液体止滞区缩小.值得注意的是，当壁面负滑移长度较大(b1=b2=－0.3h)时，液体的流速变化区仅为微缝隙厚度的三分之一，这将形成强大的流动阻力从而抑制液体更新，因此在纳米流动中需给予充分的重视.

区别于亲液型微缝隙，疏液滑移作用范围较大，取典型10μm 厚度的微缝隙为研究对象.在壁面均为正滑移的状态下，其流动特性如图6 所示.

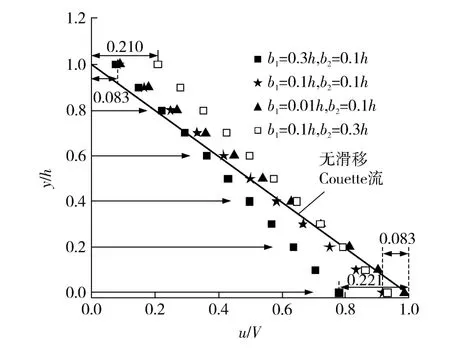
图6 疏液复合型微缝隙的典型流速分布Fig.6 Typical velocity distribution of micro-gap flow with complicated hydrophobic walls

从图中分析可知，疏液型复合界面下，同滑移长度不同壁面的滑移流速近似相等.如滑移长度b1=b2=0.1h 的情况，两个壁面的无量纲滑移流速均为0.083，即两壁面性质对滑移流动影响相同.实际工况下，若需要进行流动优化，可根据需求选取易处理的表面进行界面改性.

3 结论

结合界面滑移特性对微流动的影响规律，文中建立了亲疏液复合壁面下微缝隙剪切流的精确解模型，在CFD 建模验证其可靠性的基础上，利用该模型得到以下结论:

(1)带滑移边界的微缝隙流动在壁面(0.5 m/s)运动下，其流场存在一个发展过程，并迅速趋向于稳定状态;对于厚度为100 μm 的微缝隙，该稳定过程的时间为0.01 s.这表明对具有滑移行为的微缝隙流动，可以直接采用稳态模型进行分析.

(2)在纳米尺度下，滑移长度大的静止亲液壁呈现出强的液体附着力;若此时对应运动壁面为疏液状态，该效应将进一步增强.然而，当运动壁面为亲液、静止壁面为疏液时，亲液壁面的液体附着力减小，液体相对壁面静止的区域明显缩小.这说明对于有强附着力要求的场合，增强静止壁面的负滑移强度十分必要;反之对于低流阻要求场合则需要充分降低该类滑移的强度.

(3)疏液壁面性质对流场的作用受壁面运动影响小，尤其当微缝隙静止和运动壁面均为疏液状态时，两壁面性质对滑移流动的影响近似相同.因此，若需要改变该滑移类型的微流动状态，可选择易于表面改性的静止(或运动)壁面进行界面处理.

［1］傅新，陈晖，陈文昱，等.光刻机浸没液体控制系统的研究现状及进展［J］.机械工程学报，2010，46(16):170-175.Fu Xin，Chen Hui，Chen Wen-yu，et al.Developments and prospects of immersion control system in immersion lithography machine［J］.Journal of Mechanical Engineering，2010，46(16):170-175.

［2］姜继海.液体变粘度缝隙流动理论与解析［M］.北京:国防工业出版社，2005.

［3］刘赵淼，王国斌，申峰.基于Navier 滑移的油膜缝隙微流动特性数值分析［J］.机械工程学报，2011，47(21):104-110.Liu Zhao-miao，Wang Guo-bin，Shen Feng.Numerical analysis of oil film flow in micro gap with Navier slip boundary conditions［J］.Journal of Mechanical Engineering，2011，47(21):104-110.

［4］Schmieschek S，Belyaev A V，Harting J，et al.Tensorial slip of superhydrophobic channels ［J］.Physical Review E，2012，85(1):016324/1-11.

［5］Eric L，Howard A S.Effective slip in pressure-driven stokes flow［J］.Journal of Fluid Mechanics，2003，489:55-77.

［6］Chang H C，Chang J K.Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface ［J］.Physical Review Letters，2006，96(6):066001/1-4.

［7］Rothstein J P.Slip on superhydrophobic surfaces［J］.Annual Review of Fluid Mechanics，2010，42:89-109.

［8］Joseph P，Cottin-Bizonne C，Benoit J M，et al.Slippage of water past superhydrophobic carbon nanotube forests in microchannels ［J］.Physical Review Letters，2006，97(15):156104/1-4.

［9］Eijkel J C，Berg A V D.Nanofluidics and the chemical potential applied to solvent and solute transport［J］.Chemical Society Reviews，2010，39:957-973.

［10］宋付权，于玲.液体在润湿性微管中流动的边界负滑移特征［J］.水动力学研究与进展A 辑，2013，28(2):128-134.Song Fu-quan，Yu Ling.The boundary negative slippage of liquid flowing in hydrophilic micro-tubes［J］.Chinese Journal of Hydrodynamics，Series A，2013，28(2):128-134.

［11］胡海豹，鲍路瑶，黄苏和.不同润湿性纳米通道内库埃特流动的分子动力学模拟［J］.力学学报，2013，45(4):507-514.Hu Hai-bao，Bao Lu-yao，Huang Su-he.Simulation of the liquid coquette flow in a nano-channel with different wettability［J］.Chinese Journal of Theoretical and Applied Mechanics，2013，45(4):507-514.

［12］王馨，张向军，孟永钢，等.剪切率对微纳米间隙下流体边界滑移影响的试验研究［J］.中国机械工程，2009，20(17):2081-2084.Wang Xin，Zhang Xiang-jun，Meng Yong-gang，et al.Experimental research on boundary slip of confined liquids at micro/nano scale and effect of shear rate［J］.China Mechanical Engineering，2009，20(17):2081-2084.

［13］Asmolov E S，Belyaev A V，Vinogradova O I.Drag force on a sphere moving toward an anisotropic superhydrophobic plane［J］.Physical Review E，2011，84(2):016324/1-8.

［14］Priezjev N V，Troian S M.Molecular origin and dynamic behavior of slip in sheared polymer films［J］.Physical Review Letters，2004，92(1):018302/1-4.

［15］Zhang X Y，Zhu Y X，Granick S.Hydrophobicity at a janus interface［J］.Science，2002，295:663-666.

［16］Chiara N，Drew R E，Elmar B，et al.Boundary slip in Newtonian liquids:a review of experimental studies［J］.Reports of Progress in Physics，2005，68:2859-2897.

［17］Tretheway D C，Meinhart C D.Apparent fluid slip at hydrophobic microchannel walls ［J］.Physics of Fluids，2002，14(3):9-12.