江湖关系变化的内在机理
2014-08-16
(中国水利水电科学研究院,北京 100044)
1 研究背景
本文所提江湖关系是指荆江与洞庭湖关系。自1860年藕池口冲开、1870年松滋口冲开形成了藕池河和松滋河以来,奠定了四口分流荆江的格局,从而使江湖关系不断变化,对长江中游广大地区(枝城至武汉河段及洞庭湖)发生了深远影响。江湖关系应包括3阶段、5个方面,后者为:四口分流的径流量、分流河道冲淤、洞庭湖淤积、荆江冲淤以及城汉河段冲淤。这5个方面不仅相互作用、相互影响,而且内在机理十分复杂[1-2]。除这5个方面外,还有人为影响,如丹江口水库和葛洲坝水库兴建、荆江人工裁弯、三峡水库兴建,都有大小不同的作用,特别是三峡水库(包括以上水库群)对江湖关系更有关键性的作用。三峡工程建成后,江湖关系进入“第3阶段”,其相互影响和变化的现象如图1所示。
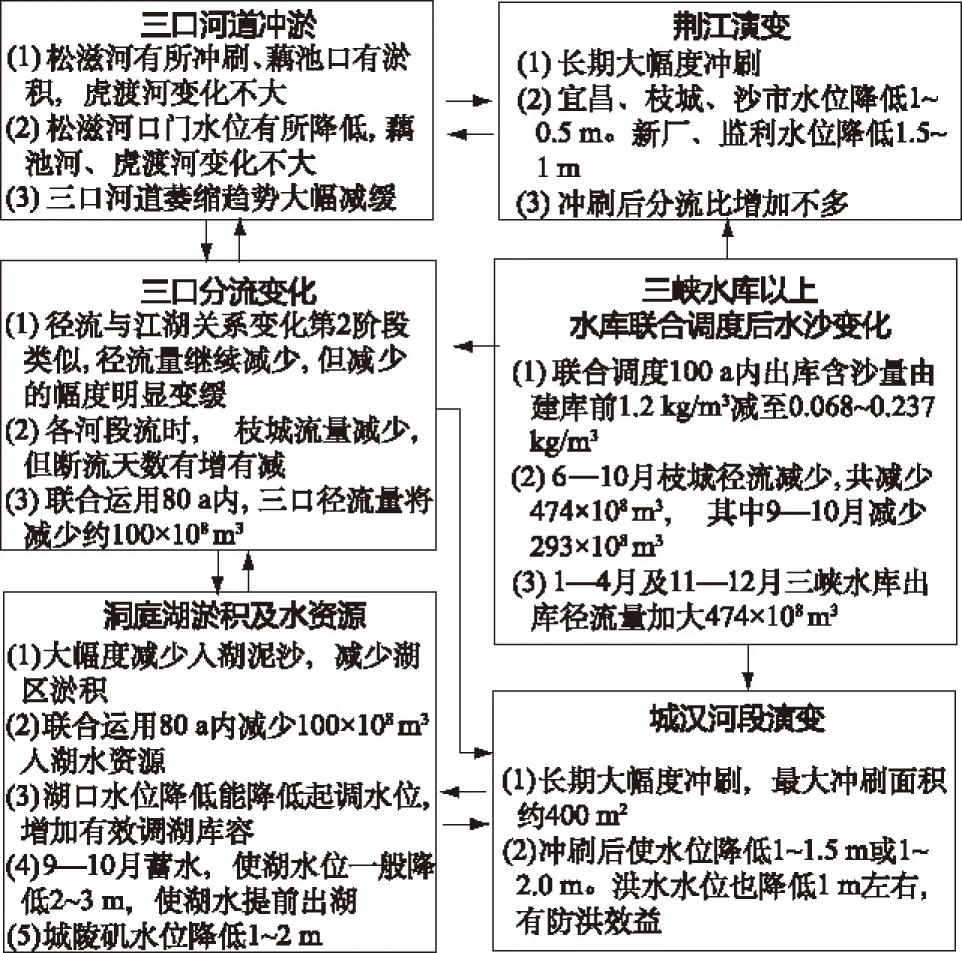
图1 三峡水库运行后“第3阶段”江湖关系内在联系
鉴于江湖关系现象的描述论文已不算少,本文只打算从理论方面深入地揭示其机理,阐述其规律。限于篇幅,本文只研究2个最关键的方面,并且主要涉及江湖关系变化的“第3阶段”。
2 荆江径流量变化及冲淤的基本规律
2.1 荆江作为分汊河道的主汊而存在
荆江与四口分流河道及洞庭湖构成了一个分汊河段,它作为这个分汊河段的主汊而存在。分汊河道的基本特点是除丰、枯水及季节性变化外,径流量还会不断变化,包括长时间的系统增加和减少。例如在江湖关系变化“第1阶段”(四口分流增加),作为主汊的荆江径流量是减少的,而作为支汊的四口河道主要是藕池河、松滋河和洞庭湖径流量是加大的。在江湖关系的“第2阶段”(四口分流减少),主汊的径流量是加大的,支汊径流量是减少的。从已有资料来看,支汊最大分流比也仅占枝城的42.9%,可见三口河道及洞庭湖始终是一个支汊。作为分汊河道,有3点值得注意:第一,分汊河道支汊的分流比是随流量的加大而加大,反映出洪水时分流比大,枯水时分流比小甚至断流;第二,支汊冲刷发展有停止的日期,支汊衰塞没有明确停止日期,这就是该河段处于江湖关系“第1阶段”短、“第2阶段”长的道理;第三,分流比变化,对于主、支汊变形均起着关键作用,但是同样数量的径流量增减,显然对支汊影响大,对主汊影响小。
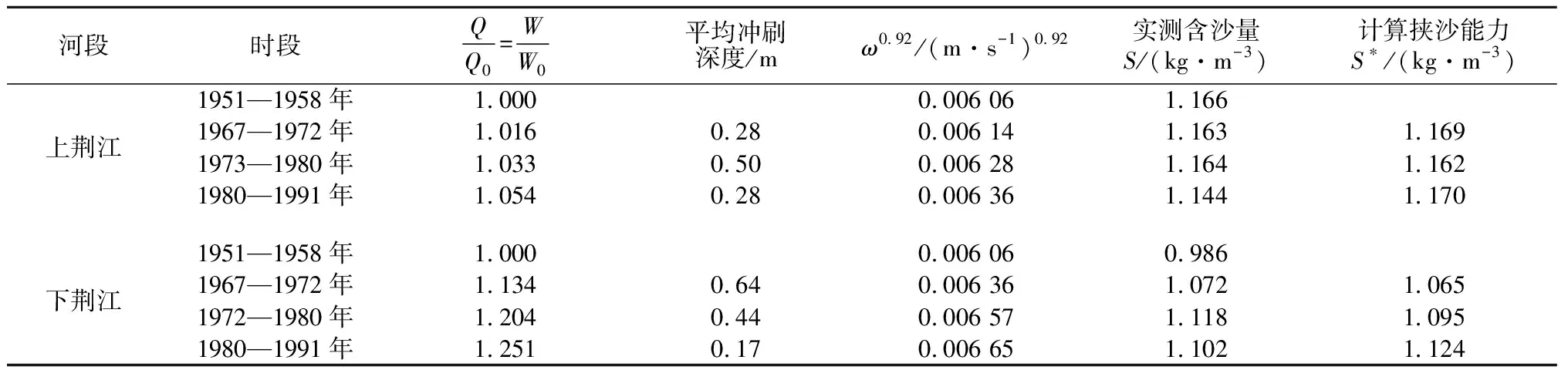
表1 上、下荆江由于径流量加大引起的挟沙能力变化
2.2 荆江裁弯—分汊河道上裁弯—的特点
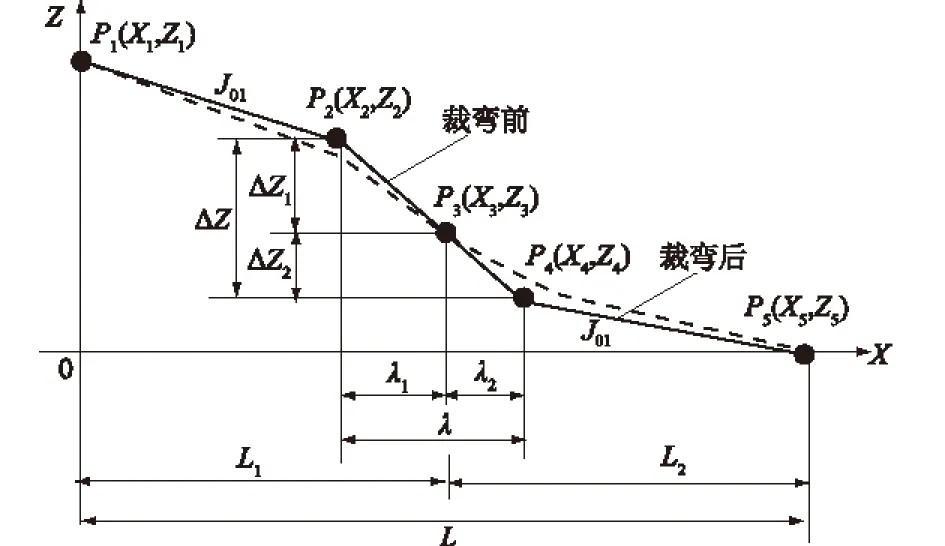
图2 裁弯后调整坡降冲刷的纵剖面
下荆江3个裁弯使河长缩短了约75 km。裁前原荆江坡降为0.352×10-4~0.554×10-4,裁时加大至0.660×10-4,从而使流速加大,产生冲刷。有人将这种冲刷作用估计很大,认为裁弯才是荆江冲刷和径流量加大的主要原因;也有相反的看法,认为裁弯对荆江影响不大。那么裁弯对冲刷影响究竟如何?对荆江径流量加大的影响又如何?如果不考虑裁弯引起径流量加大(即按单一河道裁弯),则裁弯冲刷的确不大。我们曾在理论上进行裁弯冲淤的研究(见图2)。从图2可见单一河道裁弯后是上冲下淤(如图2中虚线所示为单一河道裁弯冲刷后的纵剖面,实线为裁弯前纵剖面),将缩短河长增加的坡降向上、下相邻河段传递,达到平衡后,若取裁弯段坡降为裁弯前的1.05倍,则冲淤范围为544 km,上段冲深0.205 m,下段淤高0.157 m。冲淤总量均为5 838×104m3。但是荆江裁弯后,冲淤图形与所述裁弯理论的图形完全不一样,裁弯后1966—1982年上荆江冲刷0.78 m,下荆江冲刷2.34 m,而且裁弯以下的河段洪山头至城陵矶长达61 km,不仅没有淤反而冲刷,这与径流量不加大的单一河道的裁弯完全不同。这证明荆江冲刷主要不是裁弯加大坡降后的冲刷。但是荆江冲刷还在另一方面与裁弯有密切关系。即裁弯加大了荆江流量(与此同时减少了三口流量,特别是减少了藕池口流量),而由加大的流量引起的冲刷则是很主要的,而且这点会长期作用。这是因为流量加大又引起进一步冲刷,而进一步冲刷又进一步加大流量。
需要指出的是,了解分汊河道与单一河道裁弯的差别,今后对荆江出口处裁弯和簰洲裁弯的研究都是有好处的。显然,后者的裁弯属于单一河道的裁弯;而前者的裁弯,虽然仍在分汊河道,但是已属于分汊河道尾部,它们的变形显然与已有的荆江裁弯有所差别。
2.3 荆江流量加大引起的冲刷
单纯流量加大引起的冲刷,其挟沙能力为
(1)
式中:S为含沙量;Q为流量;S*为挟沙能力;ω为泥沙沉速。加下标“0”表示冲刷前的有关参数的值,不加下标“0”表示该时段参数的值,冲刷前含沙量的平均值S0=1.166 kg/m3。不同冲刷阶段上、下荆江冲刷过程有关水力因素及挟沙能力如表1。表中W/W0为冲刷前后年径流量比。
从表1中数据看出,由于流量加大后,计算的时段平均冲刷能力S*与实测含沙量S符合很好。这是因为流量加大是逐步的,输沙是接近平衡的,故S*与S应很接近。从而表明,荆江流量加大引起冲刷确是主要的因素。而且荆江流量加大,既包括了三口分流河道由于淤积引起入流的自然衰减,也包括了荆江裁弯引起的径流量加大。
2.4 荆江干流流量加大对三口分流河道的影响
设在初始时刻分流河道流量Q2,0与荆江流量Q1,0之比为0.3(相当于分流比0.231),则当荆江流量加大ΔQ=0.15Q1,0后,三口河道分流量的变化为
(2)
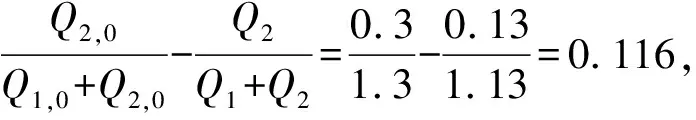
2.5 分流河道与荆江同时冲刷
当分流河道与荆江同时冲刷时,彼此应存在一定的关系。例如,可设彼此相对冲刷的面积应相近,甚至相等,这时注意到在时间缓慢冲刷过程中也应维持对系统平衡破坏最少。故而可取
(3)
取三峡水库运用后Q2/Q1≈0.075(分流比7%),则ΔA2=(0.493)3ΔA1,按数模计算荆江冲刷80 a,上、下荆江平均最大冲刷面积4 684 m2=ΔA1,则分流河道冲刷面积ΔA2=562 m2。另一方面,据数学模型计算,松滋河相应冲刷量为0.61×108m3。按河长125 km,平均冲刷面积约为488 m2。可见与上述估计基本一致。这说明松滋河会有所冲刷,但冲刷量不可能很大。
2.6 三峡水库运行后,荆江及中下游河道冲刷至平衡的出口断面的时间
下游河道冲刷由于来水来沙过程的大幅改变,在原本就复杂的下游河道变化情况下,使问题进一步复杂,对冲刷过程无法简单估计。但是冲刷过程的基本特点是由上向下发展。随着床沙粗化,水力因素减弱,水库下泄含沙量加大,冲刷会被逐渐扼制,而且远在水库淤积平衡以前。但是不少人认为下游河道冲刷被扼制,应与水库平衡时间相近。这是错误的。前者已为三峡水库下游数学模型多次计算结果所证实。现在我们采用概化方法,做一理论研究,以期反映其本质。对于下游河道的某一断面,在冲刷过程中它总会达到平衡(不再冲刷)。根据挟沙能力公式,冲刷前该断面的挟沙能力为
而冲刷至平衡
从而冲刷至平衡与冲刷前挟沙能力比
(4)
而冲刷至平衡的该断面的年输沙量
(5)
式中:V为水流平均流速;h为水深;n为糙率;g为重力加速度;J为坡降;Q为流量;β为挟沙多值性修正系数,下标“0”表示初始值。
根据一些水库实测资料,上述各参数的变化范围如下。三门峡水库下游黄河铁谢至辛寨在20世纪60年代,冲刷后n/n0加大到1.62倍,官厅水库下游永定河在50年代n/n0加大到1.45倍,丹江口水库下游在20世纪60—70年代加大到1.71倍。当然这3组资料都在下游河道的上段,但是其中的床沙也有中、细沙河段。变化也很大,丹江口水库下游汉江襄阳在20世纪50—70年代,平均沉速加大至1.354/0.354=4.37倍,仙桃加大至0.526/0.204=2.58倍。三峡水库运用后2006年较之建库前,监利站平均沉速也已加大到1.67/0.384 =4.35倍(相应的床沙中大于0.1 mm已占60%)。现在取监利水文站资料作为代表荆江出口断面,并采用建库前该站ω0=0.384 cm/s,冲刷至极限ω=4×0.384=1.536 cm/s<1.67 cm/s,建库前年均输沙量QS,0=3.63×108t,n/n0=1.45,h/h0=1.1,J/J0≈1,以及由于恢复饱和系数变化引起的挟沙能力多值性的调整参数β=0.574。后者是采用我们最新的理论成果。

0.051 8×3.63=0.188×108t 。
这就是监利(荆江出口)冲刷至平衡的输沙量(其ω为1.536 cm/s)。另一方面从水库排沙看,当运用91~100 a,水库排沙1.051×108m3(平均沉速ω为0.252 cm/s),折合成监利的平均沉速,则相当的排沙量为1.051×108×0.252/(4×0.384)=0.172×108t ,小于监利站的输沙能力,因此监利以上还会冲刷。但是若三峡水库运用101~110 a,则出库沙量为1.17×108t(平均沉速0.256 cm/s),则折合监利的输沙量为1.17×108t×0.256/(4×0.384)=0.195 0×108t,可见采用两者平均值0.184×108t(相当于105 a)与监利输沙量0.188×108t,基本一致,不再需宜昌至监利再产生冲刷。当然这里没考虑荆江分流入洞庭湖和洞庭湖出湖沙量,由于沙细、数量小,这种影响可以不计。
现在分析汉口站的情况。汉口站床沙要细,水力因素也弱一些,可取ω/ω0=3,n/n0=1.2,汉口建库前输沙量为4.04×108t,ω0=0.275 cm/s。从而冲刷至平衡的输沙量为
0.435×108t 。
而121~130 a水库出库沙量1.33×108t×0.269/(0.275×3)=0.434×108t,可见两者非常接近。误差不过1%。至此,汉口站冲刷至极限时年平均输沙量为0.435×108t(沉速0.825 cm/s),与出库沙量1.33×108t(ω=0.269 cm/s)或者折合0.434×108t(ω=0.825 cm/s)是平衡的,因此汉口以上几乎不会再冲刷。上述估算与数学模型计算结果,即城陵矶以上在80~100 a几乎平衡(相对值在0.998~1.006)、城陵矶至汉口100 a尚有冲刷趋势是一致的。而且由于泥沙粗细不同,监利平衡输沙量小,汉口平衡输沙量大,这与数学模型计算也是一致的。
2.7 监利输沙量变化的估计
由于随着冲刷进行,冲刷量是不断衰减的,设冲刷与当时冲刷量Ws成反比,与Δt成正比,α为衰减系数,则有
即
Ws=Ws,0e-αt。
(6)
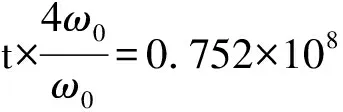
即
Ws=2.08e-0.010 7t。
其中平衡时间采用95 a。按上式积分可得累计淤积量,即

3 分流河道演变的基本规律
3.1 分流河道作为三角洲上的河道
荆江四口分流河道不是一条普通的河道,它是最复杂的一种河道[3]。除前面提到的,它作为分汊河道的支汊外,尚有2种重要的特性,使它可同时称为三角洲上的河道与季节性的河道。

图3 淤积引起的水位抬高示意图
分流河道具有三角洲上的河道的属性是很明显的,因为它们的下段就是洞庭湖的变动回水区。河道以淤积为主。淤积具有向下游延伸、向上抬高及向上游翘尾的特点[4](如图3)。同时淤积还会不断横向摆动,淤出大片滩地和残留一些新的汊河。其中值得注意的是松滋河1873—1954年81 a间,三角洲顶点下延约70 km;藕池河1860—1900年,三角洲顶点下延65 km。其次淤积与回水后翘,也在不断发生,并且从图中看出的淤积引起新的回水要超过原有回水的末端。如图中的x5~x6就是淤积引起的回水抬高超过了原来的末端。这正是当淤积尚未到达分流河道口门时,回水的影响也可能达到口门,而减小了分流比。
3.2 季节性的河道形成——断流的机理
当分流河道与荆江分流比相差很大时,前者就会在枯水期发生断流,而变为季节性河道。由于
(7)
则可得到如下关系
即
(8)
其中ξ为河相系数,下标“2”代表分流河道进口有关参数,下标“1”代表分流后荆江有关参数。对于不同的Q2/Q1,求出了它们的水深比如表2。可见只要Q2/Q1<1,则分流河道水深小于干流的。

表2 不同分流比参数计算值
现在求断流条件(如图4)。若要分流河道断流,应满足如下水深条件:
h2,M (9) 图4 分流河段断流示意图 式中:h1,m为分流后荆江最小水深;h1,M,h2,M分别为荆江和分流河道最大水深。对于上荆江有关参数可取n=0.021,J=0.55×10-4,ξ=3.85,则当Q1,M=50 000 m3/s时,由上述公式可求出h1,M=12.2 m。 相应地设Q1,m=3 000 m3/s时,h1,m=(Q1.m/Q1,M)3/11×12.2=5.65 m;Q2,M=4 500 m3/s,h2,M=(Q2,m/Q1,M)3/11×12.2=6.33 m。可见6.33 m<6.55 m(12.2 m-5.65 m),故断流。另设式(9)取等号,于是有 h1,c=h1,M-h2,c(Q1,c) , 即 (10) 式中:h1,c为支汊开始断流时主汊的临界水深;Q1,c为相应的临界流量。这大体相当松滋河情况,即Q1=3 000 m3/s断流;但Q1>3 420 m3/s不断流。 现在按式(10)分析藕池口的断流情况。取Q1,M=47 500 m3/s,Q2,M=1 200 m3/s,则由前述有关数据有h1,M=12.03,h2,M=4.41 m,设Q1,m=5 000 m3/s,则h1,m=(5 000/47 500)3/11×12.03=6.51 m,满足h2,m=4.41 m<5.58 m(12.09 m-6.51 m),故断流。现在由式(4)至式(8)求出Q1,c=8 897 m3/s。按实测资料2003—2012年藕池河分流比0.024,断流流量8 910 m3/s(管家铺)。这与前面估算结果是符合的。 分流河道淤积的原因首先是由于分流引起。 由挟沙能力公式 (11) 或者注意到式(8) (12) 其中ω2,0是入分流河道口门的沉速,可用分流前荆江干流的沉速ω1。在表2中,算出了不同分流比η2=Q2/(Q1+Q2)条件下有关参数。包括分流后支汊与主汊的流量比Q2/Q1,水深比h2/h1以及挟沙能力比。从表2中可见,由于支汊分流比小,而使平均水深、挟沙能力均明显降低,这正是“分流则淤和支汊发生淤积的原因”。 (13) 式中ω2为分流河道(不再分汊的单一河道)淤积平衡后的沉速;λ为淤积平衡时的淤积百分数,即 (14) 当已知Q2/Q1,ω2(λ)则由表3的关系插补。分流河道淤积量与干流分流前输沙量的比为 (15) 表3 枝城悬移质级配分选 此处η2为发流河道的分流比。 现在取松滋河情况分析,设Q2/Q1=0.075,则h2/h1=(Q2/Q1)3/11=0.493,故 式中:ω(λ)表示ω是λ的函数,经试算λ=0.160。而λ0=0.075/1.075λ=0.011 2,取三峡水库运用前1999—2002年枝城输沙量为34 600×104t,则该分流河道淤积ΔWs=0.011 2×34 600×104t≈388×104t,占该分流河道分进沙量2 850×104t的13.6%。从这个数值看,其淤积百分数似乎略小,这是未考虑其进一步分汊的情况。 分流河道,并不是单一河道,它们还会进一步分汊。如松滋河在湖北为2条河,在湖南又分为3条河。藕池河由两汊不断发展为三汊、四汊。甚至有称藕池河有大小六汊,从而称三口河道在湖南有10条河。分流河道再分汊后,输沙能力还会进一步减小,而淤积会进一步增加。根据我们研究,如果一条单一河道,当分成k条汊道后,设各汊道的水力因素相同,则有下述关系[3]: (16) 式中:下标“2”表示分流河道的参数,K表示分汊的数量,ξ2表示分流河道(作为单一河道)河相系数,ξ3表示进一步分汊后的河相系数,据分析进一步分汊后河相系数会有所加大。可取为ξ3/ξ2=1.10。这样式(16)为 于是 (17) 即淤积百分数为 选取1967—1972年代表中等分流的情况,此时枝城年平均径流量4 490×108m3,三口河道总分流1 053×108m3,分流后荆江径流量为3 437×108m3,故(Q2/Q1)3/11=0.3063/11=0.724=h2/h1,于是由上式当分为相同两汊时,K=2,则 经试算λ=0.138,ω=0.269 2 cm/s。从而λ0=0.306/1.306×0.138=0.032 3,该时段枝城的输沙量为51 900×104t,故分流河道淤积ΔW=1 678×104t,占同期分流河道入口输沙量的15 000×104t的11.2%。但是若分成相同的三汊,则 经试算,λ=0.160,ω=0.244 7 cm/s。ΔW=0.037 5×51 900×104t≈1 946×104t,即占分流河道入口输沙量的15 000×104t的13.0%。据长江水利委员会荆江局由地形图计算1952—1995年的43 a中,三口分流河道淤积量为5.69×108m3,折合7.68×108t,则年淤1 786×104t。这在前述按K=2~3的分流河道年淤积量1 678×104~1 945×104t之间。可见估算与实测是符合的。 另外,估算三峡水库运用前1999—2002年资料,枝城径流量为4 454×108m3,分流径流量为345×108m3,分流后荆江径流量4 109×108m3,故(Q2/Q1)3/11=0.508 8,当K=2时 于是λ=0.21,λ0=0.077 5×0.21=0.016 3,枝城输沙量34 600×104t,故松滋河淤积为546×104t,占进入松滋河输沙量2 850×104t的19.8%。该时段藕池河径流量155×108m3分流后荆江径流量为4 299×108m3,分流前荆江输沙量为32 800×104t。经试算当K=3时 求出λ=0.310,ω=0.165,λ0=0.31×0.348=0.010 8,故ΔW=0.010 8×32 800×104t≈354×104t,占同期进入藕池河输沙量的1 800×104t的19.7%。从前面估计的淤积比看,单条分流河道比约20%,和一些实测资料基本符合。例如,1955—1985年资料分析结果[3],松滋河淤积比18.8%。藕池东支16.2%等。 前面例子指出分流河道淤积时,其淤积比超过20%是很不容易的。这得益于淤积过程中,粗的颗粒淤积的多、细的颗粒淤积少的分选作用。也就是说随着淤积,由于沉速减少而挟沙能力加大。但是如变为冲刷,情形就不一样,即令不考虑级配变粗,则分流河道的挟沙能力也很小。此时当K=2,Q2/(Q2+Q1)=0.075,忽略级配变化,则由式(5)至式(17)松滋河的输沙能力为 表4 三峡出库枝城站及三口分流河道含沙量 可见,藕池河进入的含沙量已与挟沙能力0.273 kg/m3相近,可见略有淤积是正常的。至于松滋河,进入含沙量明显小于其挟沙能力0.418 kg/m3,当然会产生一些冲刷,但数量不会很大。 上述分析未考虑床沙粗化。现在适当补充说明。三峡水库出库级配按正常运用前10 a计算,其平均沉速为ω=0.178 cm/s。而按前述枝城天然条件(相当平衡)悬移质平均沉速为ω=0.418 cm/s,设由床沙补给的ω=2×0.418 cm/s,于是2003—2012年松滋所进入的悬沙的平均沉速为 尚需说明的是,此处取天然条件下沉速ω=0.418 cm/s,是与枝城平均含沙量1.10 kg/m3相应的,而冲刷后是考虑粗化后为ω3的挟沙能力。可见按表4中松滋河前3个时段入口的实际含沙量均小于冲刷时挟沙能力0.279 kg/s,故而产生冲刷;而藕池河4个时段入口的含沙量均大于冲刷挟沙能力0.163 kg/m3,故不可能产生冲刷。另一方面,如按接近平衡考虑,则其挟沙能力为0.248 kg/m3,则有2个时段可能冲,2个时段可能淤积。而在100 a内,还是淤积多,故该河看来会有少量累计淤积。上述估计与数学模型计算结果也是一致的。 三峡水库建成前,江湖关系变化的第2阶段,荆江冲刷、分流河道淤积,导致分流河道径流量迅速的减少。文献[4]指出,分流比为负指数递减,除裁弯使该递减率达到0.030 7/a~0.032 1/a外,第2阶段递减率平均值0.016/a。另据数学模型计算,三峡水库运用后80 a三口分流由594×108m3减少至493×108m3,则年递减率为0.002 33/a,仅为1/6.87。即三口分流量W=594×108m3e-0.002 05t,t以年计。进一步指出,当经过50 a按第2阶段的四口分流递减率,则三口分流将减少327×108m3;而按数模计算的第3阶段递减率,四口分流则仅减少65.3×108m3。为什么与建库前差别这样大?当然以前一淤一冲,现在两者均冲,在定性上应该减慢,但定量上若不说清楚无法理解,而产生质疑。由下述关系 A=ξ2h3, 得到 (18) 于是对分流河道流量与荆江之比为 (19) 下标“0”表示冲刷前的,A表示过水面积。冲刷一段时间后, (20) 其中ΔA是经冲刷扩大的过水断面。上式可写成 (21) 前面已证实,如冲刷的发展是尽可能对平衡没有大的破坏,ΔA2/A2及ΔA1/A1应相近。虽然冲刷不可能完全达到平衡,荆江冲刷是主导的方面,故ΔA2/A2,0会仍略小于ΔA1/A1,0,从而说明了在江湖关系第3阶段,分流河道径流量会继续减少,但减少会很慢。 当然这里分析的是一种平均情况,如发生断流甚至长时间断流,需要修正。这就是说如果中小洪水防洪运用太多,导致分流比明显偏离平均值,实际分流比减少要快一些。 (1) 本文为了克服对江湖关系实际资料的统计分析和数学模型计算2种途径研究的不足,将江湖关系最重要的2个方面,分成14个问题分别从理论上深入揭示其内在机理,给出了定量结果,使复杂的现象具有清楚内涵和明确的内在联系。克服了经验资料的分析机理含糊,缺乏一般性等不足;同时也避免了数学模型只能简单地给出数学结果的问题。因此,本文不仅在江湖关系机理研究方面有较全面的新成果,而在研究途径上也有所创新。 (2) 本文的分析,侧重于理论概括和机理阐述,不刻意追求数字的十分准确。但是得出的结果在一定误差内又是可靠的,这可从文中的结果与实际资料和数模计算对比看出。 (3) 本文的分析,不仅在较短时期能描述江湖关系内在机理及各种表现,而且能分析较长时间变化趋势,这是理论研究考虑因素较多的结果。可以认为本文给出了江湖关系在50~100 a内变化的轮廊。 参考文献: [1] 韩其为.洞庭湖三口分流河道及江湖关系调查研究[R].北京:中国水利水电科学研究院,1997.(HAN Qi-wei. Investigation on the Relation Between Jingjiang River and Three Out-flowing Streams into Dongting River[R]. Beijing: China Institute of Water Resources and Hydropower Research, 1997. (in Chinese)) [2] 韩其为.江湖流量分配变化导致长江中游新的洪水形势[J].泥沙研究,1999,(5):1-12.(HAN Qi-wei. Changes of Flood Situation Along the Middle Yangtze River[J]. Journal of Sediment Research, 1999,(5): 1-12. (in Chinese)) [3] 韩其为,周松鹤.三口分流河道的特性及演变规律[J].长江科学院院报,1999,(5):5-8. (HAN Qi-wei, ZHOU Song-he. Characteristics and Fluvial Processes of Diffluent Rivers from Yangtze River to Donting Lake[J]. Journal of Yangtze River Scientific Research Institute, 1999, (5): 5-8. (in Chinese)) [4] 韩其为.水库淤积[M].北京:科学出版社,2003.(HAN Qi-wei. Reservoir Deposition[M]. Beijing: Science Press, 2003. (in Chinese))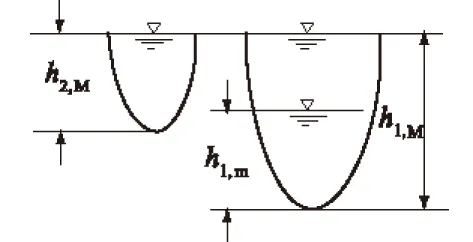
3.3 分流引起淤积的原因
3.4 分流河道内的进一步淤积
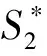

3.5 分流河道进一步分汊后的淤积
3.6 分流河道冲刷时挟沙能力会大幅度减少
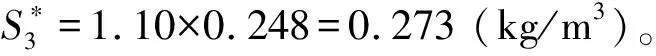
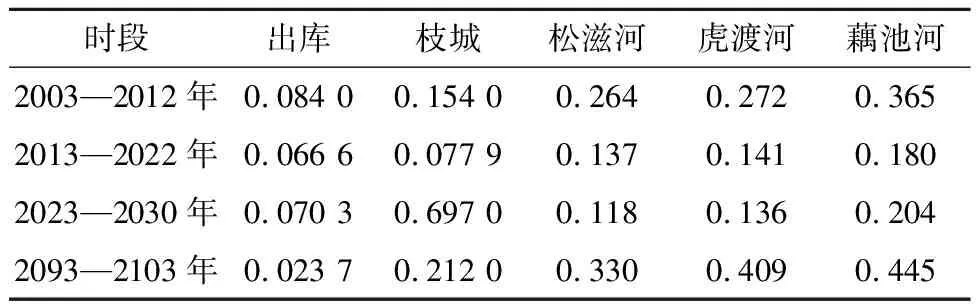
3.7 三峡水库运行后分流河道径流量减少幅度大幅变缓
4 结 论
