对流层水平梯度对PPP的影响

曹文涛，郭际明，谢 翔，周命端，贾效燕

(1. 武汉大学 测绘学院，湖北 武汉 430079； 2. 武汉市测绘研究院，湖北 武汉 430022)

一、引 言

目前，GPS水汽观测大多采用双差网解法实时或准实时的估计对流层延迟，然而，要想获取测站的绝对对流层延迟，必须引入超远的GPS 参考站(>500 km)，但会增加数据解算的难度和时间，从而不利于GPS 技术在当今实时水汽遥感和天气预报中的应用[1]。与常用的双差估计对流层延迟方法相比，精密单点定位估计方法具有估计模型简单、站站之间不相关、无需引入远距离测站即可估计绝对时延、处理大规模数据速度快等优点，适合实时或近实时处理GPS水汽观测的数据[2]。

本文基于PPP方法，利用参数估计对流层延迟，分析比较在不同气象条件和不同截止高度角情况下，施加对流层水平梯度改正与否对PPP定位结果的影响。

二、对流层延迟参数估计法

在稳定的气候条件下使用模型函数法可以很好地改正对流层延迟，但大气中的水汽变化通常变幻莫测，这时，无论模型中使用的是标准大气参数还是实测气象参数，往往都无法反映真实的垂直大气状态。因此在高精度GPS数据处理时，将模型改正值作为先验值，然后将天顶延迟的剩余误差作为待定参数，与待定点坐标以及其他未知量一起求解估计，叫做参数估计法[3]。

对流层折射影响通常表示为天顶方向的对流层折射量R和同高度角相关的投影函数M的乘积。并且对流层延迟中90%左右是干分量延迟；只有10%左右是由水汽引起的湿分量延迟。因此，对流层延迟可用天顶方向的干、湿分量延迟及其相应的投影函数表示，即

ΔRtrop=ΔRz,dryMdry(E)+ΔRz,wetMwet(E)

(1)

式中，E为卫星高度角；ΔRtrop为对流层总延迟；ΔRz,dry为天顶对流层干分量延迟；Mdry(E)为天顶对流层干分量投影函数；ΔRz,wet为天顶对流层湿分量延迟；Mwet(E)为天顶对流层湿分量投影函数[4]。

对流层延迟影响利用模型改正后, 干分量部分的改正精度可以达到厘米级，而湿分量部分的残余影响还比较大。在PPP中，通常利用参数估计的方法将对流层湿分量的残余影响当做一个参数进行估计。

另外，实测的大气折射率剖面可以为参数估计提供参考。这种方法不仅可以消除模型改正的系统误差，而且还可以很好地模拟大气折射的随机误差，提高PPP定位的精度。

三、对流层延迟水平梯度改正

式(1)是基于大气层在各方向上是均质的这一假设。但是，大气层并不是在各方向上均质的，因此研究人员提出了另一种对流层延迟模型，这种模型增加了水平梯度改正项[5-6]。

ΔG=Mgrid(E)cotE·GNcosΦ+Mgrid(E)cotE·

GEsinΦ

(2)

式中，ΔG为水平梯度改正项；Φ为测站到卫星的方位角；Mgrid(E)为梯度投影函数；GN为南北向的大气梯度参数；GE为东西向的大气梯度参数[7-11]。

将式(1)、式(2)联合起来，即为附有水平梯度改正的对流层延迟模型。

四、算例分析

本文采用IGS武汉站2011年9月4日与9月7日两天的观测数据，采样历元为30 s，以及IGS公布的这两天的事后精密星历和精密钟差。这两天的天气状况对比见表1。

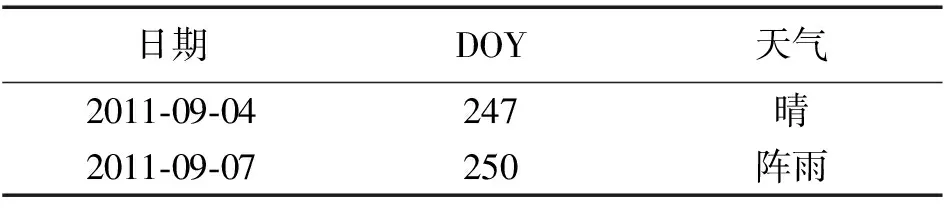
表1 天气信息表

基于参数估计对流层延迟的方法，在施加水平梯度改正和不施加水平梯度改正这两种情况下，利用rtklib开源软件分别处理9月4日和9月7日两天的观测数据。采用的数据处理策略为(两天采用同样的数据处理策略)：

1) 3°高度角，无水平梯度改正；

2) 3°高度角，有水平梯度改正；

3) 5°高度角，无水平梯度改正；

4) 5°高度角，有水平梯度改正；

5) 7°高度角，无水平梯度改正；

6) 7°高度角，有水平梯度改正；

7) 10°高度角，无水平梯度改正；

8) 10°高度角，有水平梯度改正；

9) 15°高度角，无水平梯度改正；

10) 15°高度角，有水平梯度改正。

表2为不同高度角情况下，PPP解算结果与IGS公布的武汉站坐标(视为真值)在N、E、U 3个方向上误差的平均值及其RMS，其中数据解算结果从模糊度稳定后开始分析；高度角信息栏中，G代表施加了水平梯度改正；NG代表没有施加水平梯度改正。

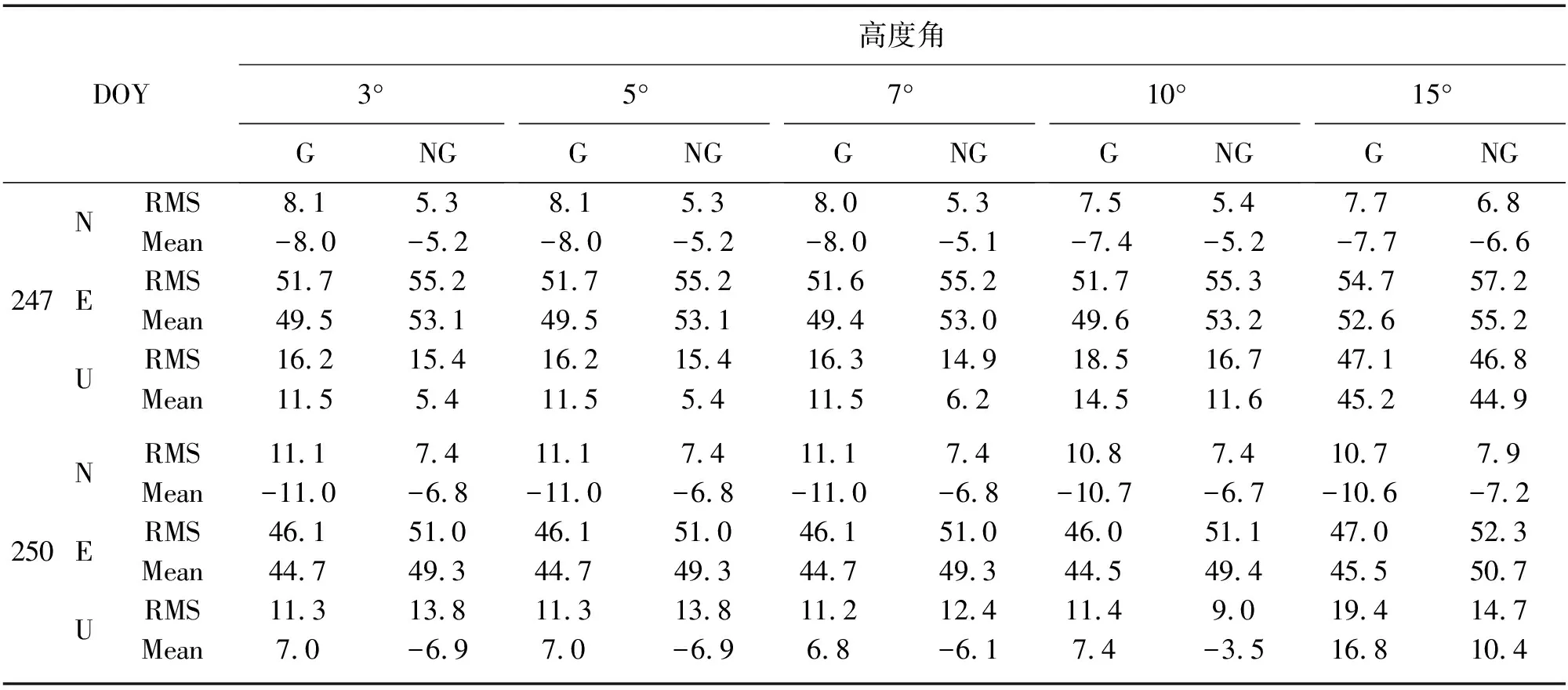
表2 不同高度角下N、E、U偏差的平均值和RMS mm

为了讨论不同天气和不同截止高度角情况下，对流层水平梯度改正对PPP定位结果的影响，将DOY247与DOY250两天的结果进行横向对比，如图1—图4所示，图中无梯度改正表示为No Gradient，施加梯度改正表示为With Gradient。

由图1—图4可以看出，当高度角一定且不施加水平梯度改正时，水平方向上的RMS总体上都是随着高度角的增加而增加，其RMS相差3 mm左右，且差值随着高度角的增加而无较大波动；U方向上的RMS差值在低高度角时十分相近，仅为1 mm左右，但随着高度角的增加，差值可增大到32 mm；点位误差变化与U方向的变化类似，低高度角时差值较小，而随着高度角的增加也可增大到30 mm。

图1 N方向偏差的RMS

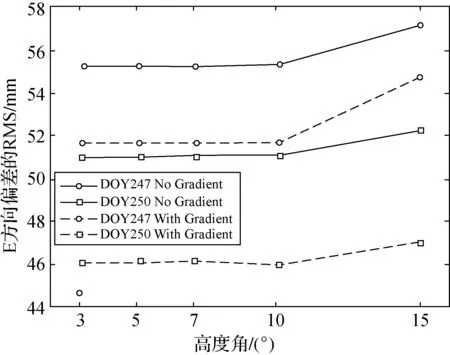
图2 E方向偏差的RMS

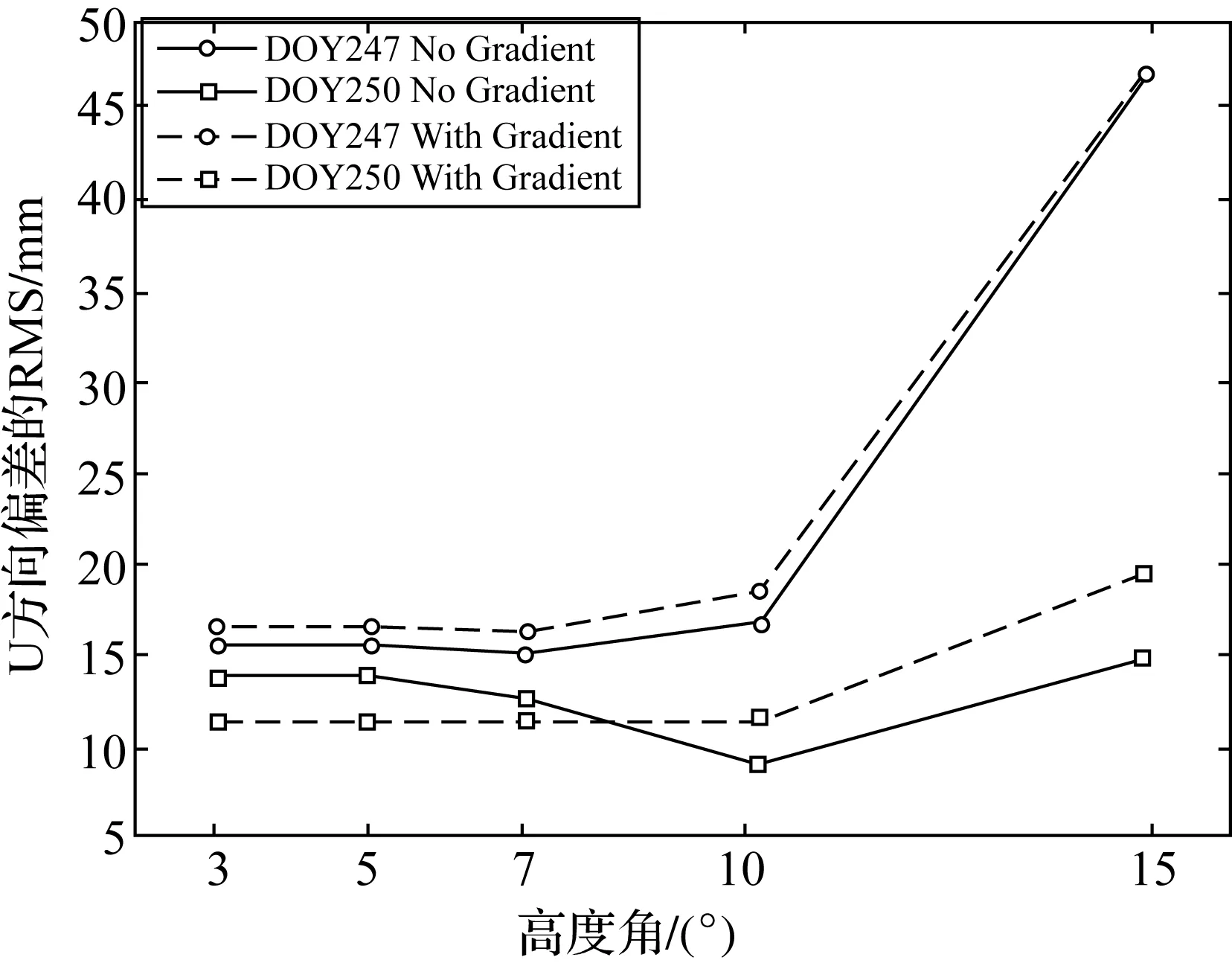
图3 U方向偏差的RMS

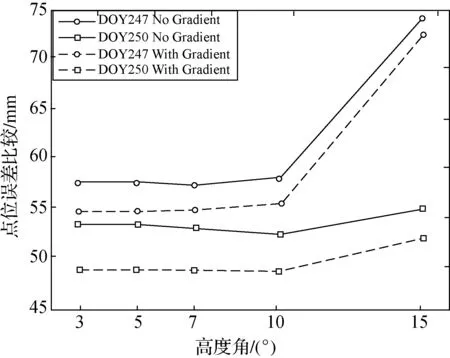
图4 点位误差比较

当高度角一定且施加水平梯度改正时，各方向上的RMS变化规律与点位误差变化规律与不施加水平梯度改正时的类似。但是，N方向的RMS整体比不施加水平梯度改正时增加了3 mm左右；E方向的RMS则整体比不施加水平梯度改正时减少了5 mm左右；U方向上，天气晴朗时，施加水平梯度改正与否对RMS几乎没有影响，而阴雨天气时，施加梯度改正在低高度角时可降低RMS，而随着高度角的增加，RMS反而比不施加梯度改正时要高。点位误差在低高度角时，施加水平梯度改正对精度提高的效果明显；而随着高度角的增加，精度提高的效果则减弱，且阴雨天气比晴朗天气精度提高的效果明显。

五、结 论

本文基于PPP技术，讨论在利用参数估计对流层延迟的情况下，施加对流层水平梯度改正与否在不同天气条件和高度角时对定位结果的影响，可得出以下结论：

1) 在阴雨天对流层湿度变化剧烈时，在低高度角情况下，施加水平梯度改正可以使天顶U方向的RMS降低，并且有利于提高点位精度，且效果均较晴朗天气明显；在高度角较大时，施加水平梯度改正可以有效地抑制点位误差的增加。

2) 无论天气条件如何，当截止高度角较低时，施加水平梯度改正对点位精度有较明显的提高。

3) 无论天气条件如何，随着高度角的增加，N、E、U方向上的RMS和点位误差基本上都会随之变大。

经过以上讨论可以看出，施加水平梯度改正，对精密单点定位的精度略有提高，尤其是在阴雨天、低高度角的情况下。

参考文献：

[1] 李黎，匡翠林，朱建军，等. 水平梯度和映射函数对PPP对流层延迟估计的影响分析[J].工程勘察, 2011,39(5): 52-56.

[2] 叶世榕，张双成，刘经南.精密单点定位方法估计对流层延迟精度分析[J].武汉大学学报：信息科学版,2008, 33(8)：788-791.

[3] XIE Y X，LAVERGNAT J．Microwave and Millimeter Wave Propagation [M].[S.l.]:International Academic Publishers,1995:58-63.

[4] 施展，孟祥广，郭际明，等. GPS精密单点定位中对流层延迟模型改正法与参数估计法的比较[J]. 测绘通报, 2009(6): 9-11.

[5] CHEN G， HERRING T A. Effects of Atmospheric Azimuthal Asymmerty on the Analysis of Space Geodetic Data [J]. Journal of Geophysical Research, 1997, 102(B9): 20489-20502.

[6] BAR-SEVER Y E，KROGER P M，BORJESSON J A. Estimating Horizontal Gradients of Tropospheric Path Delay with a Single GPS Receiver [J]. Journal of Geophysical Research,1998,103(B3):5019-5035.

[7] 丁晓光. 对流层延迟改正在GPS数据处理中的应用和研究[D]. 西安：长安大学, 2009.

[8] TEKE K, BÖHM J, NILSSON T,et al.Multi-technique Comparison of Troposphere Zenith Delays and Gradients during CONT08 [J]. Journal of Geodesy, 2011,85(7): 395-413.

[9] GHODDOUSI-FARD R, DARE P, LANGLEY R B. Tropospheric Delay Gradients from Numerical Weather Prediction Models: Effects on GPS Estimated Parameters[J].GPS Solution, 2009,13(4):281-291.

[10] 许承权，吴绍祖. 对流层梯度改正模型及其对GPS精密单点定位的精度影响分析[J].闽江学院学报, 2009, 30(2):95-98.

[11] MEINDL M, SCHAER S, HUGENTOBLER U, et al. Tropospheric Gradient Estimation at CODE: Results from Global Solutions[J].Journal of the Meteorological Society of Japan,2004,82(1B):331-338.