基于Von Mises分布的PPP宽巷相位偏差计算方法

赵兴旺，张翠英

(安徽理工大学 测绘学院，安徽 淮南 232001)

一、引 言

精密单点定位(precise point positioning,PPP)技术能够实现RTK的定位效果，但整周模糊度确定是数据处理的一个重要环节。由于观测值中初始相位和仪器设备硬件延迟的存在，被模糊度吸收使得非差或单差观测值的模糊度不再具有整数的特性。在这种情况下，若以模糊度解算方法本身的适用性作为一种工具加速精密单点定位收敛，必须对它进行严格的建模改正，以便恢复非差或单差模糊度的整周特性。针对这一问题，国内外专家作了深入研究，目前主要存在两类实现方法：一类为估计分解卫星钟差法，如加拿大NRCan的Collins等人[1]从钟差估计的角度吸收相位偏差的小数部分，但需要对卫星钟差进行参数估计，计算复杂；另一类为非整相位偏差法，如美国德克萨斯州大学的Gabor[2]、德国GFZ的Ge[3]，以及我国的张小红[4-6]、张宝成[7-8]等对PPP模糊度固定进行了研究，这些研究均是基于模糊度与相位偏差分离的基础实现PPP模糊度固定的，并且德国斯图加特大学的Cai[9]，荷兰代尔夫特理工大学的Keshin[10]的研究表明，GPS相位值具有方向数据的性质。

为了建立合适的估计模型、有效分离相位偏差实现PPP固定解，必须对这些相位偏差做出清晰的认识。因此，本文从整数与小数分离的角度，对相位偏差小数的特性进一步研究，寻求科学合理的相位偏差小数计算方法，最后对算例进行分析。

二、相位偏差

GPS载波相位观测量中除了钟差影响、大气误差等传统误差外，还包含了初始相位偏差和硬件延迟。文献[11]给出了伪距和载波相位两种观测量，其观测方程如下

(1)

(2)

式(2)中，δr、δs分别为接收机端和卫星端的载波相位硬件延迟；φr(t0)和φs(t0)分别为接收机端和卫星端初始相位；其余参数含义参见文献[11]。

由式(2)知，数据处理时初始相位和载波相位硬件延迟与模糊度参数合并为一个参数，而消除其影响、维持模糊度为整数常用的方法是在星间与站间建立双差观测值。但这对于PPP技术并不适用，因为站间差分无法消除与卫星相关的这部分偏差影响，因此必需对其进行严格的标定、检测或建模修正，才能实现PPP单差模糊度的固定解。

1. 相位偏差处理原则

由于初始相位和载波相位硬件延迟均对载波相位模糊度产生直接影响，为了研究的方便，本文将它们统称为相位偏差。于是，将载波相位观测方程式(2)中的模糊度项进一步表示为

(3)

在PPP星间差分模型中，相位偏差整数部分对模糊度的整周性质不产生影响，可以与模糊度合并为一项处理，而剩余小数部分严重破坏了模糊度的整数性质[12]。对它们的处理通常是建立在整数与小数有效分离的基础上。根据相位偏差的形成机理可知，对于不同测站，星间差分模糊度应该具有近似相等的相位偏差小数部分。因此，可以按照常规PPP模式和M-W组合模型对观测网数据进行联合解算，利用较大范围覆盖的少量观测站数据估计相位偏差。

宽巷观测值的模糊度具有长波长的特点，受误差的影响相对较小，且方便求取，所以本文以宽巷模糊度为例对其进行相位偏差分离和分布特性分析。由观测方程式(1)和式(2)分别形成载波相位宽巷组合和伪距窄巷组合，表达式如下

(4)

(5)

将式(4)和式(5)相减消除公共误差后便得到宽巷模糊度表达式

(6)

对上式进一步变换得到

(7)

由于码延迟与宽巷模糊度相位偏差不可分离，但相关研究表明当模糊度解算时可以忽略这部分偏差[3]。为了消除接收机相位偏差δφwr的影响，在卫星i和卫星j之间组成单差载波相位宽巷模糊度，表达式为

(8)

2. 相位偏差小数单位圆表示

相位偏差一般由整数和小数两部分组成，在单位圆上表示如图1所示。图1(a)中相位偏差为δφ=0.5=0.5-1=-0.5，这意味着一个由整周数为0、小数部分为0.5组成的相位偏差等同于一个由整周数为1、小数部分为-0.5组成的相位偏差，这种数据在圆上表现出周期性。如前后两个历元i和i+1的相位偏差为δφi=112.2和δφi+1=111.9，在单位圆上表示如图1(b)、(c)所示。对于这样的偏差如何取得正确的小数部分呢？正确的取法为δφfrac,i=0.2，δφfrac,i+1=0.9-1=-0.1。这是因为在一个连续弧段内，载波相位模糊度通常由唯一的整数部分和缓慢变化的相位偏差小数部分组成。

图1 相位偏差小数方向特性示意图

为了获得这样的相位偏差小数部分，可采用函数GPHASE将其整数部分移除[2]，表达式为

δφfrac=GPHASE(N+δφ)=

(9)

式中，δφfrac为相位偏差小数；arctan()为反正切函数；N为整周模糊度参数；δφ为相位偏差项。

采用式(9)得到的相位偏差小数部分，既保证了相位偏差小数的大小，又保证了正确的象限位置，其变化区间为[-0.5,0.5]周内。

三、偏差小数的分布检验

直线上的分布一般不存在周期性的问题，而从相位偏差小数在圆上表示的方式可以看出具有方向数据的某些性质。Von Mises分布是方向数据统计中最重要的分布，它在圆上分布族中的地位与高斯正态分布在直线上分布族的地位相当。在方向数据统计理论中，参数估计、假设检验等方面多以Von Mises分布为前提。为了对相位偏差进行科学、合理的分析，首先需要对相位偏差序列是否服从Von Mises分布进行验证。本文将从宽巷相位偏差序列的均匀性、拟合度，以及直方图与分布拟合曲线多方面对其进行分布假设检验分析。

1. Von Mises分布

Von Mises分布一般表示为VM(μ,k)，其密度函数为

(10)

2. 均匀性检验

均匀性检验是检验数据样本是否来自均匀分布，由于均匀性分布是Von Mises分布的退化情形(k=0)，因此，首先判断相位偏差序列并非来自均匀分布。对于给定的偏差序列，它的位置参数μ为未知值，所以原假设H0和备择假设H1可写为

(11)

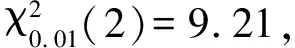
表1 BJFS站均匀性检验统计信息表

3. Pearson χ2拟合度检验

Pearsonχ2拟合度检验是常用的拟合度检验，其原理是寻求一个反映实际观测数据θ1,θ2，…,θn与理论分布F0(θ)之间偏差的统计量Δ，如果Δ超过某个界限，则拒绝理论分布F0(θ)。于是可将相位偏差数据的拟合度检验表示为

H0:F=F0(θ);H1:F≠F0(θ)

(12)

建立检验统计量为

(13)

式中，fi为θ1,θ2,…,θn在给定区间的实际频数；pi为由理论分布F0(θ)计算θi在给定区间的概率；m为样本空间划分的区间个数。

对于给定的置信水平α，式(12)的拒绝域为

(14)

式中，s是未知参数的个数。

对于Von Mises分布拟合度检验，只需将F0(θ)变为VM(μ,k)，其中平均方向μ和尺度参数k采用最大似然估计值代替。为了检验相位偏差序列是否服从Von Mises分布，对2010年04月11日BJFS站数据的相位偏差进行Von Mises分布和正态分布的拟合度检验。因此，本文根据偏差情况合理的分为36个区间，计算结果见表2。由表2可知，当置信水平α=0.000 1时，具有偏差个数较多的卫星对服从Von Mises分布，而不是直线域上的正态分布。对于偏差个数较少时，如表2中卫星对PRN14-PRN18由于相位偏差样本中个数较少、不能反映出分布的具体特性，难以区分Von Mises分布与正态分布。可见，基于Von Mises分布对相位偏差分析更为合理，但在相位偏差计算时应采用较多历元的观测数据，根据试验分析本文建议至少采用200个历元的观测数据。

表2 BJFS站相位偏差拟合度检验

4. 直方图与分布拟合曲线

通常用绘制直方图来确定随机变量所近似满足的分布。尽管直方图不能给出较为精确的样本密度估计，但能简单、直观地反映出总体分布的特征。同样采用BJFS站2010年04月11日观测数据确定的相位偏差小数序列绘制出直方图，并且分别按照Von Mises分布、正态分布的密度函数对偏差序列进行曲线拟合。图2分别为PRN21、PRN22、PRN26、PRN27 4颗卫星(参考于PRN18卫星)的单差相位偏差小数分布的直方图与拟合曲线图。从图中曲线的整体形状可以直观地看出，Von Mises分布能够与直方图保持很好的一致性，特别是能较好地覆盖边缘区域，这部分主要是相位偏差估计时由于误差噪声等原因产生的相位偏差反向突变，即当相位偏差真值为0.45周、噪声为0.08时，相位偏差变为0.45+0.08=0.53，经式(9)后偏差小数变为-0.47。这种现象表明，采用线性方法计算将出现错误的均值，这也是本文寻求新的计算方法的原因。

图2 偏差小数直方图

5. 偏差小数计算方法

通过对相位偏差数据序列进行检验分析可知，相位偏差小数更好地服从Von Mises分布。因此，为了得到更精确的相位偏差小数估值和标准差，将所求得的包含相位偏差的整周模糊度项作相应变换，于是有

(15)

式中，n为参与计算的模糊度个数。

经过式(15)中三角函数作用后，整周模糊度与相位偏差整数部分均被移去，仅剩下相位偏差小数部分，式(16)为相位偏差小数计算表达式

(16)

相应的标准差为

(17)

四、算例分析

为了验证相位偏差计算方法的可行性，本节将对宽巷相位偏差估计精度和空间分布进行分析。试验数据选取中国及周边区域的BJFS、CHAN、WUHN、TNML、TWTF、PETS、TEHN、ARTU、IISC等18个IGS跟踪站，2010年第101天的观测数据进行分析，采样率为30 s，其中测站点PETS和TEHN具有最大站间距，约7500 km左右，测站点TNML和TWTF的站间距最小，约25 km左右。

根据观测值的起止时间定义所有可能出现的单差宽巷模糊度，采用式(16)和式(17)计算宽巷相位偏差估值及标准差。

图3为BJFS站2010年第101天所有卫星参考于PRN31卫星的单差宽巷相位偏差估值。点代表卫星的相位偏差估值，很明显相位偏差并不为零。在没有经过相位偏差改正的情况下，单差模糊度往往不具备整数性质，不能直接被固定。误差条表示该相位偏差值的标准差，变化范围为0.001～0.060周，表征了相位偏差估计的稳定性。图3中虚线表示相位偏差估计时参与计算的单差模糊度个数，可以明确地看出参与个数越多，相位偏差估值的标准差越小。

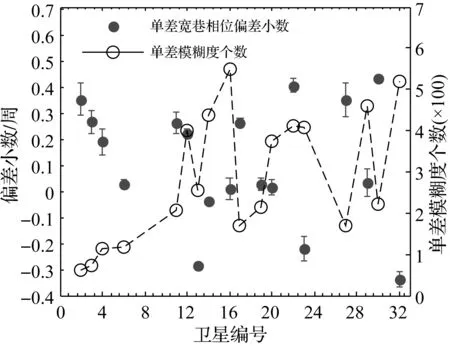
图3 SDW-FPB估值(参考于PRN18卫星)

相位偏差估计是基于Von Mises分布对多个测站的相位偏差求平均方向来确定最终估值。因此，相位偏差在各个测站间表现出的空间一致性将关系到相位偏差估计的准确性，并进一步影响相位偏差改正在广域范围内应用的有效性。为了分析相位偏差估值在空间上的稳定性，采用2010年第101天的观测数据对相位偏差进行试验分析。图4为PRN26卫星(参考于PRN18卫星)15个测站偏差估值与总体平均方向(作为相位偏差最终估值)的差异统计图，虚线部分表示测站点与BJFS站的站间距离，实线表示与偏差最终估值之差。

图4 PRN26单差宽巷偏差各站比较图

由图4可知，距离BJFS站最远点为ZECK，站间距约6000 km，与BJFS站相位偏差之差为-0.015 7周；距离BJFS最近点为CHAN，站间距约920 km，与BJFS站相位偏差之差为-0.0161周。并且在所有站点中与最终偏差估值相差最大值为0.050 4周，该组数据的均方根误差(RMS)为0.026周。可见，测站间距从920～6000 km不等的各测站相位偏差与平均方向相差很小，在空间上保持很好的一致性。

五、结束语

本文以统计假设检验理论为基础，从相位偏差序列的均匀性、拟合度及直方图与分布拟合曲线多方面验证了相位偏差小数更好地服从Von Mises分布，并给出了基于Von Mises分布的相位偏差小数计算方式。该方法可有效避免因误差噪声导致相位偏差小数反向突变的现象，保证相位偏差小数估值的客观性。本文算例表明宽巷相位偏差受区域影响很小，对于超过几千千米的参考网，利用本文给出的方法求取相位偏差具有较高的精度和空间稳定性，能够用于精密单点定位中相位偏差改正，以实现PPP固定解。

参考文献：

[1] COLLINS P. Isolating and Estimating Undifferenced GPS Integer Ambiguities[C]∥Proceedings of ION NTM 2008.San Diego, CA:[s.n.]， 2008: 720-732.

[2] GABOR M, NEREM R. GPS Carrier Phase Ambiguity Resolution Using Satellite-Satellite Single Differences[C]∥ Proceedings of ION GPS 1999.Nashville TN:[s.n.]，1999: 1569-1578.

[3] GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations [J]. Journal of Geodesy, 2008, 82(7): 389-399.

[4] 蔡昌盛,李征航,张小红.GPS系统硬件延迟修正方法的探讨[J].测绘通报,2002(4):15-16.

[5] 张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验[J]. 武汉大学学报：信息科学版, 2010, 35(6): 657-660.

[6] LI X, ZHANG X, GE M. Regional Reference Network Augmented Precise Point Positioning for Instantaneous Ambiguity Resolution [J]. Journal of Geodesy, 2011, 85(3): 151-158.

[7] 张宝成, TEUNISSEN J G P, ODIJK D，等.精密单点定位整周模糊度快速固定[J].地球物理学报,2012,55(7):2203-2211.

[8] 张宝成,欧吉坤.论精密单点定位整周模糊度解算的不同策略[J].测绘学报,2011,40(6):710-716.

[9] KESHIN M. Directional Statistics of Satellite Satellite Single Difference Widelane Phase Biases[J]. Article Satellites,2004, 39(4): 305-324.

[10] CAI J, GRAFAREND E, HU C. The Statistical Property of the GNSS Carrier Phase Observations and Its Effects on the Hypothesis Testing of the Related Estimators[C]∥Proceedings of ION GNSS 2007.Fort Worth, TX, USA：[s.n.]，2007: 331-338.

[11] TEUNISSEN P J G, KLEUSBERG A. GPS Observation Equations and Positioning Concepts [J].Lecture Notes in Earth Sciences: GPS for Geodesy, 1996, 60(5): 175-217.

[12] 潘树国,赵兴旺,王庆.单差PPP相位偏差估计方法及有效性分析[J].宇航学报,2012,33(4): 436-442.

[13] JAMMALAMADAKA S R, SENGUPTA A. Topics in Circular Statistics [M]. Malaysia: World Scientific Publishing, 2001: 33-56.