高铁桥墩沉降预测方法研究

龚循强，熊小容，周秀芳

(1. 西南交通大学 地球科学与环境工程学院，四川 成都 610031； 2. 四川省应急测绘保障与地质灾害监测工程技术研究中心，四川 成都 610041； 3. 贵州地矿工程勘察有限公司，贵州 贵阳 563200； 4. 四川农业大学 经济管理学院，四川 成都 611130)

一、引 言

高速铁路基本采用“以桥代路”的方式建设，因此严格控制高速铁路的桥墩沉降量是保证列车高速、安全、舒适运行的关键因素。从某种程度上讲，通过对高速铁路前期沉降的实测，预测出后期的沉降量是否满足高速铁路设计和运营要求，能够有效地指导下一步的工作并保障列车的安全运行。因此，深入研究高铁桥墩沉降预测方法对高速铁路安全有着十分重要的指导意义。本文在对自回归模型参数的最小二乘(least squares, LS)估计进行理论研究的基础上，提出一种自回归模型参数的稳健最小二乘(robust least squares, RLS)估计方法，并结合工程实际数据，分别采用LS和RLS的自回归模型、自适应过滤法及灰色预测法对高铁桥墩沉降进行模拟与预测，在对前期沉降数据进行模拟分析的基础上，预测后期数据，将模拟和预测结果与实际沉降值进行比较分析。

二、高铁桥墩沉降预测方法

目前，常用的静态预测方法有双曲线法、三点法、抛物线法等；动态预测方法则有时间序列法、自适应过滤法、灰色系统法、人工神经网络法等[1-3]。但由于高速铁路施工对工程所处的地质和环境破坏较大，易使沉降体随时间变化出现不同程度的沉降，因此使用动态预测方法进行高铁桥墩沉降预测较为合理。

1. 稳健最小二乘的自回归模型

自回归模型在动态数据处理中有着广泛的应用，它通过对各类动态数据建立相应的数学模型，并对模型进行研究分析，以了解这些数据的内在结构和特性，从而对数据变化趋势做出正确的分析预报[4]。设有按时间顺序排列的样本观测值x1，x2，…，xn，p阶自回归模型的误差方程可表示为

自回归模型参数一般采用LS求解[5]，可得β的LS解为

显然自回归模型的LS估计对数据中的异常值未能考虑，而在测绘数据采集中，异常值普遍存在。尝试采用RLS进行自回归模型参数的估计，通过合理调整权因子来减少异常值对平差结果的影响，从而提高估计结果的可靠度。自回归模型的RLS参数估计具体迭代解算步骤如下：

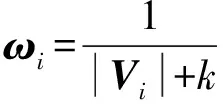
4) 利用式(3)计算自回归模型的RLS参数的估值；

2. 自适应过滤法

自适应过滤法的基本过程是先选取一组初始权数；然后计算得到预测值和预测误差；再根据一定公式调整权数以减少误差，经过多次反复迭代，直至选择出“最佳”权数[6-7]。设x1,x2,…,xt为某一时间序列，则有如下时间序列的一般预测模型

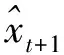
运用自适应过滤法调整权数的计算公式为

3. 灰色预测法

灰色系统理论GM(1,1)模型是针对符合光滑离散函数的一类数列建模[8-9]。设非负离散数列x(0)，对其进行一次累加生成序列x(1)，对此生成序列建立一阶微分方程

(6)

按LS求解得

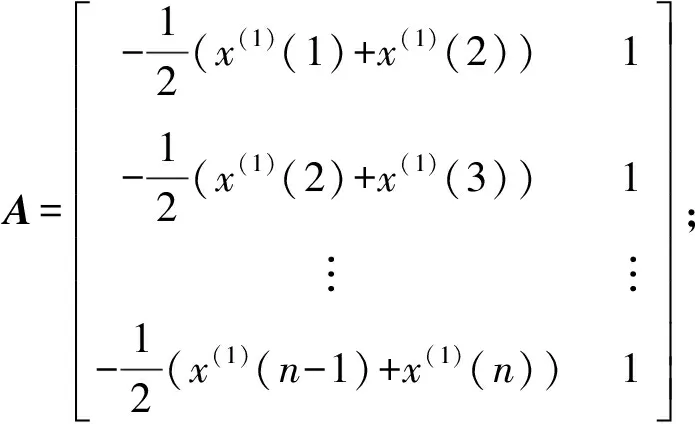
式(8)即为灰色预测基本模型。

三、实例分析

前文中简要介绍了自回归模型、自适应过滤法和灰色预测法，并阐述了采用LS和RLS进行自回归模型参数估计的方法。下面结合真实工程数据，分别利用LS和RLS的自回归模型、自适应过滤法及灰色预测法对高铁桥墩进行沉降预测。

以某城际铁路特大桥区段的某桥墩2011—2012年间每周定期进行的20期沉降观测值为例，比较各种方法预测的精度。利用前10期的实测值作为原始数据进行模拟，对后10期数据进行预测。为方便比较，沉降量以亚毫米为单位。

首先采用线性假设法[10]确定模型的阶数p为1，接着分别利用LS和RLS进行自回归模型参数的估计，根据参数估计结果建立高速铁路桥墩沉降观测的自回归模型，从而对沉降数据进行模拟及预测。同时采用自适应过滤法和灰色预测法对数据进行模拟与预测，并将各种方法的模拟、预测结果(见表1和表2)与实际沉降值进行比较分析。

表1 各种方法的模拟值对比分析

续表1

表2 各种方法的预测值对比分析

从表1可以看出，各种方法的模拟精度相当，但RLS的自回归模型模拟精度优于LS，且以自适应过滤法为最优。从表2可以看出LS的自回归模型、自适应过滤法和灰色预测法短期预测效果较好，但随着预测时间的延长，预测结果则不可靠。而RLS的自回归模型预测结果却很稳健，预测精度明显优于其他3种方法。

通过对各种方法的比较分析发现，自适应过滤法起源于统计学，根据预测误差不断调整权数，因此具有较高的模拟精度，但其仅对序列进行纯数学的处理，对权数的调整未考虑异常数据的影响，较适于周期性序列的预测。灰色预测法是贫信息系统建模的有效途径，但有一定的适应场合，其长期预测效果明显受到时间系列长度的限制。

自回归模型在动态数据处理中具有广泛的应用性，但目前对自回归模型参数估计方法通常采用计算简单却未顾及异常值的LS，而在数据采集中异常值难以避免，它的存在会直接对参数估计结果产生影响。因此，采用LS进行自回归模型的参数求解显然是不严密的。RLS的自回归模型能够抵抗观测值中的异常值，使异常值对模型本身影响不大，因此较LS预测结果更加接近工程实际观测值，故可认为考虑异常值的RLS预测结果更加可靠。

四、结束语

在高速铁路的建设与运营管理中，沉降控制至关重要，它是保障列车安全、高速和平稳运行的必要条件。本文提出一种自回归模型参数的RLS估计方法，并结合工程实际数据，进行高铁桥墩沉降模拟与预测。通过与LS的自回归模型、自适应过滤法和灰色预测法的比较分析研究，可得出如下相关结论：

1) 在预测次数较少的情况下，LS的自回归模型、自适应过滤法和灰色预测法对沉降数据预测精度较高，但随着预测次数的增加，误差积累越多，尤其是异常值的积累，使得结果产生变异，预测结果不可靠。

2) 采用RLS进行自回归模型参数估计的精度较高，通过迭代方法合理地抵抗了数据中普遍存在的异常值，预测结果更加接近工程实际沉降值，这说明RLS的自回归模型更适用于高铁桥墩沉降预测。

参考文献：

[1] 明祖涛, 游振兴, 张届，等. 高速铁路桥隧沉降预测模型的研究 [J]. 测绘通报， 2011(8): 17-19, 41.

[2] 明祖涛, 莫懦, 游振兴，等. 高速铁路路基沉降预测模型的研究 [J]. 测绘通报， 2012(9): 61-64.

[3] 钟汉青, 丁建勋, 马德富. 非线性沉降预测模型参数计算研究 [J]. 测绘通报， 2012(5): 68-70.

[4] 刘大杰, 陶本藻. 实用测量数据处理方法 [M]. 北京: 测绘出版社, 2000.

[5] 邱卫宁, 陶本藻, 姚宜斌，等. 测量数据处理理论与方法 [M]. 武汉: 武汉大学出版社, 2008.

[6] 周雄鹏. 自适应过滤法的原理、程序和应用[J]. 预测, 1985(2)：39-44.

[7] 周雄鹏. 一种近代时间序列预测模型—自适应过滤法 [J]. 外国经济与管理, 1986(3)：39-41.

[8] 尹晖. 时空变形分析与预报的理论和方法 [M]. 北京: 测绘出版社, 2002：50-51.

[9] 李秀珍, 孔纪名, 王成华. 灰色GM (1,1)残差修正模型在滑坡预测中的对比应用 [J]. 山地学报, 2006, 25(6): 741-746．

[10] 陆立, 许建宣. 建筑物变形监测的自回归分析法 [J]. 工程勘察, 2004(5): 61-63.