利用Google Earth高程提取构建多项式拟合似大地水准面

杨翼飞，曾丽娟

(1. 广西壮族自治区地理国情监测院，广西 南宁 530023； 2. 广西经贸职业技术学院，广西 南宁530022)

一、引 言

利用全球平滑的全球重力场模型，通过移去-恢复法进行区域似大地水准面的构建，已是多年来现代大地测量的研究热点。EGM2008超高阶全球重力场模型、CHAMP&GRACE卫星、SRTM/DTM2006.0地形等数据精度的提高，区域CORS系统的构建和多星座多频GPS接收机的研发，使得快速获取高精度大地高成果成为可能。我国多地构建了省级似大地水准面模型，这些似大地水准面几乎都采用移去-恢复法移去大地水准面外围质量，以确保采用经典的斯托克斯二维卷积公式求取模型化的似大地水准面，再将模型化的大地水准面外围质量恢复重构，兼顾均衡地形模型改正、海潮和固体潮改正等，以达到确定高精度大范围似大地水准面模型[1]。这些似大地水准面模型成果主要由省级测绘主管部门管理，一些市(县)级单位想要快速获得相应成果，在服务推广和安全应用上仍需完善；同时省级似大地水准面的构建需要兼顾省一级成果的平滑，从而会牺牲一些区域的成果精度，这就降低了这些区域的精度。因而，通过利用曲面拟合方式结合EGM2008全球重力场模型，兼顾考虑均衡地形因素影响，构建市(县)一级似大地水准面，具有更好的工程便捷性和适用性。

常用的曲面拟合方式有三次样条曲线拟合法、分区最小二乘平面拟合法、二次多项式曲面拟合法、移动的二次多项式拟合法、Hardy多面函数拟合法[2]、Zernike多项式拟合法，本文主要阐述对某丘陵区进行似大地水准面的构建，采用二次多项式曲面拟合法的方式，利用平滑的EGM2008全球重力场数据和离散的高精度几何水准成果对试验区进行曲面拟合，以构建该区域的似大地水准面，为当地基础工程测量提供便捷，具有现实的应用和经济意义。

二、基本原理

多项式拟合的一般形式为

z=f(x,y)=b0+b1x+b2y+b3x2+b4xy+b5y2+b6x3+b7x2y+b8xy2+b9y3+…

(1)

式中，b0,b1,b2，…为多项式待定系数。常用的多项式拟合方式为一、二阶多项式，本丘陵区域采用的是二阶多项式拟合，即z=b0+b1x+b2y+b3x2+b4y2。由误差传播定律可知，二阶多项式拟合等式通过多组已知数据的观测，获得多余观测量，其误差方程为

由最小二乘原理知其最小二乘解为

令x1i=x,x2i=y,x3i=x2,x4i=y2，故而由式(2)可得

zi=b0+b1x1i+b2x2i+b3x3i++b4x4i

(4)

由最小二乘法方程矩阵求解，获得观测值X、Y的矩阵形式为

综合式(2)、式(4)、式(5)，可得多项式拟合的最小二乘解为

多项式拟合普遍应用于测绘领域， AH Dodson和AJ Mannucci曾分别针对GPS的对流层天顶延迟比例因子和电离层总电子含量应用多项式曲面拟合内插；挪威的H. Nahavandchi[4]通过1700个地面GPS台站和三次样条拟合的最小二乘配置法实现了挪威全国5 cm精度的似大地水准面；澳大利亚的G Fotopoulos[5]利用覆盖澳洲的900个地面GPS台站和GPS/水准多项式曲面拟合的方式获得澳大利亚20 cm精度的似大地水准面。这些应用证明，在一定区域内，采用多项式曲面拟合可取得较高精度的似大地水准面成果。

三、实例分析

本次似大地水准面构建区域为典型丘陵区，存在一小部分山地。整个丘陵区范围约为40 km×48 km，笔者通过使用Google Earth(简称GE)遥感影像获取所在区域的高程值，如图1所示。从图中可知，该丘陵区东北部为山地区，高程高于1000 m，通过数据的遴选和剔除，将高程高于600 m的山地剔除出该丘陵区，得出约30 km×40 km的图2区域。本次试验本采用SRTM/DTM2006.0的剩余地形模型数据进行山地区数据的剔除，后将GE遥感影像获取的高程和通过GAMIT软件获取的SRTM/DTM2006.0地形数据与几何水准成果进行比较，发现GE遥感影像的解译高程精度普遍优于SRTM-3(3弧秒，90 m)，在本丘陵区中的精度甚至优于SRTM-1(1弧秒，30 m)[6]，GE遥感影像的精度较差(见表1)，区域的中误差为24.50 m(为确保数据安全性，经纬度取2位小数)，整体精度优于SRTM-1，因此在山地区数据剔除时采用GE遥感影像解译高程代替SRTM/DTM2006.0地形数据。

图1 GE遥感影像获取的高程分布图

图2 剔除山地区的高程分布图

表1 Goolge Earth遥感影像解译高程和几何水准高程较差

通过山地区的数据剔除，确定该试验区均为丘陵区，避免了高程异常突变的发生，减少了二次多项式曲面拟合粗差和噪声的影响，提高了整体拟合精度和质量。确定试验区后，利用美国国家地理空间情报局(US National Geospatial-Intelligence Agency，NGA)发布的EGM2008地球重力场模型获取试验区平滑的高程异常值，如图3所示，该试验区在EGM2008下的高程异常值在18.8～19.4 m之间，由东南向西北方向高程异常绝对值渐大，呈阶梯状。而从有关文献可知，EGM2008在广西有30多厘米的系统偏差[7]，因而，需要利用等级水准点进行拟合，才能将EGM2008下的高程异常应用于测绘工程项目。

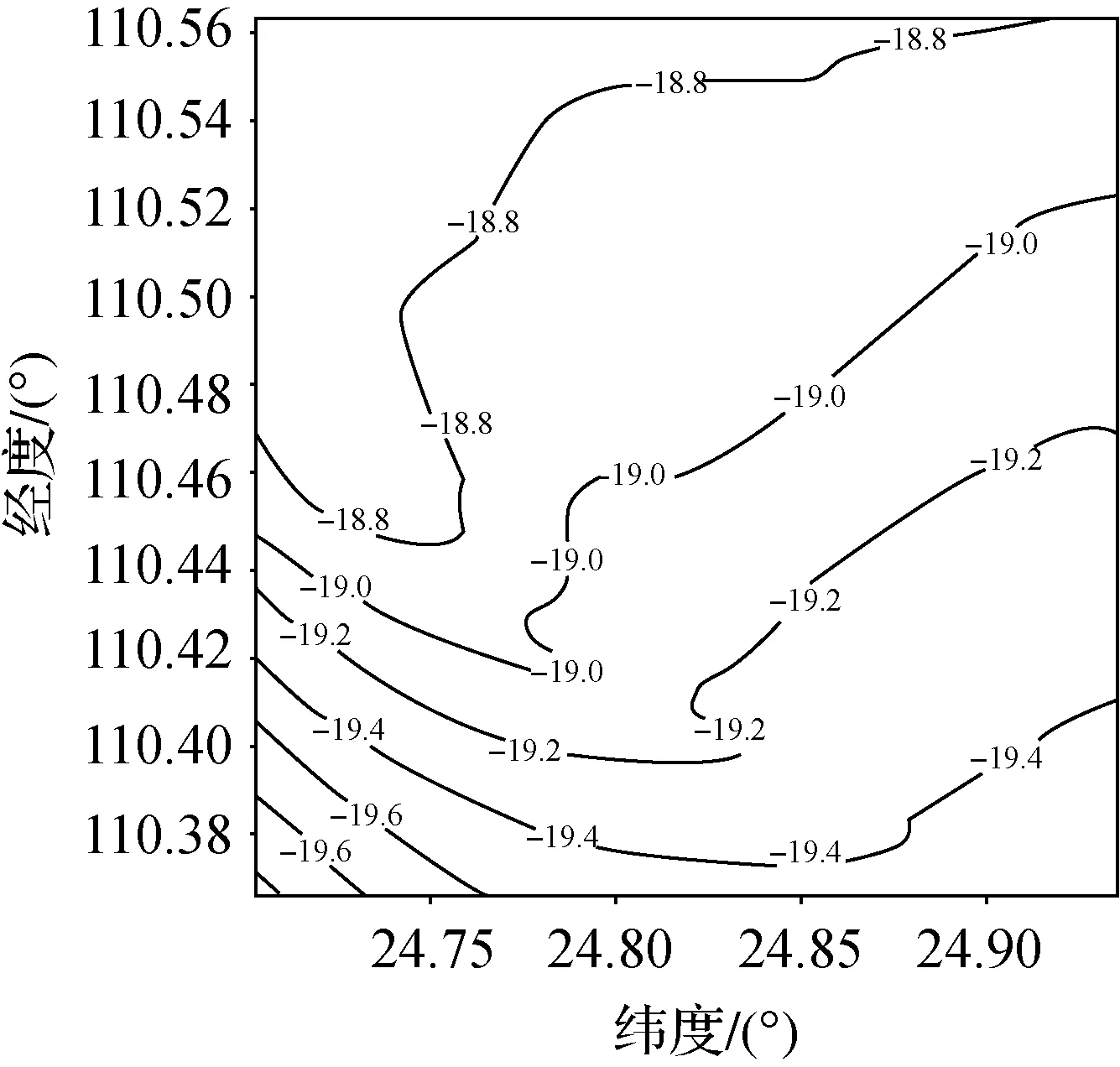
图3 EGM2008下的试验区高程异常分布图

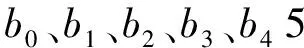
图4 水准点在EGM2008格网分布情况

表2 二次多项式曲面拟合系数及标准差值

通过二次多项式曲面拟合，得到结合EGM2008平滑高程异常和几何水准的二次曲面，如图5所示。利用该拟合的结果对所在区域进行验证，笔者选取该试验区内的10个几何水准成果，将该多项式曲面拟合的结果和几何水准的成果进行比较，整体误差较小，其中误差为3.8 cm，满足一般工程测量的需求。

图5 二次曲面拟合结果

四、结束语

本文根据似大地水准面构建的一般原理，考虑到一般误差的影响，通过利用GE高分辨率遥感影像的高程值来剔除山地区，确保应用最小二乘二次多项式曲面拟合方程的合理性，结合实例得到以下相关结论：

1) 通过二次多项式曲面拟合，兼顾EGM2008地球重力场模型和几何水准，得到整个区域的精度达到3.8 cm。

2) 在高分辨率遥感影像覆盖的区域，由于GE影像更新速度较快，在没有其他分辨率更高的DEM或DOM的情况下，考虑用GE影像具有一定的辅助意义。

本试验剔除了较多不利影响因素，得到了较好结论，但在实际过程中，由于地形是变化复杂的，应充分考虑地形因素(直接和间接影响，应引入地形改正Helmert/RTM组合法)，高程异常突变，几何水准误差(特别是多期几何成果的综合应用)，固体潮、海潮、岁差和章动等因素的影响，同时兼顾精确大地高的获取、分区拟合的必要性等，以得到最优的、收敛的区域似大地水准面成果。

参考文献：

[1] 李建成，陈俊勇,宁津生,等.地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉：武汉大学出版社，2003.

[2] 罗志才，陈永奇,宁津生.地形对确定高精度局部大地水准面的影响[J].武汉大学学报：信息科学版，2003，28(3)：340-344.

[3] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社，2003.

[4] NAHAVANDCHI H, SOLTANPOUR A. Improved Determination of Heights Using a Conversion Surface by Combining Gravimetric Quasi-geoid/Geoid and GPS-levelling Height Differences [J].Studia Geophysica et Geodaetica， 2006，50(2)：165-180.

[5] FOTOPOULOS G, FEATHERSTONE W E, SIDERIS M G. Fitting a Gravimetric Geoid Model to the Australian Height Datum via GPS data[J]. Gravity and Geoid, 2002(11): 173-178.

[6] 张兴福,刘成.综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J]. 测绘学报， 2012，41(1)：25-32.

[7] 杨翼飞，唐长增.基于EGM2008地球重力场模型的广西似大地水准面优化研究[J].测绘通报,2014(1):50-53.