Brown自检校模型相关性分析与改进

杨韫澜，韩 玲，胡海彦

(1. 长安大学,陕西 西安710054; 2. 61363部队，陕西 西安 710054; 3. 信息工程大学地理空间信息学院,河南 郑州 450052; 4. 地理信息工程国家重点实验室,陕西 西安 710054; 5. 西安测绘研究所,陕西 西安 710054)

一、引 言

1965年,美国摄影测量学者Duane C. Brown通过大量试验，对近景相机各种几何畸变进行了深入分析[1]，给出了改正成像畸变的补偿模型

在此基础上，后续研究者也做了大量卓有成效的工作[2-5]。Brown模型最初是为胶片式相机设计的，但实践已经表明其对于数字相机也适用。

Brown自检校模型中的各种自检校参数，也称为附加参数。大量附加参数的使用补偿了各种确定和不确定误差，同时也带来了各种相关性，并在一定程度上有可能降低平差精度，相关研究随着模型的提出一直未曾中断。本文在分析Brown模型相关性的基础上，对模型进行了改进，并进行试验验证，结果表明改进模型的自检校效果更好。

二、Brown自检校模型改进

Brown提出的自检校模型在近景摄影测量中作为“标准”已普遍应用，但Brown 模型存在一个问题，即参数间的强相关性。这里分析该模型的强相关性对自检校的影响，并给出改进后的新模型。

1. Brown自检校模型

Brown自检校模型中的参数包括内部定向参数(Δx0,Δy0,Δf)、径向畸变参数(K1,K2,K3)及偏心畸变参数(P1,P2)等。

(1) 径向畸变

对于大多数相机而言，径向畸变是最主要的几何误差，它是由每个独立镜头组件间的折射率差异引起的，径向畸变是对称的，且有正有负，对应的二维像空间改正量为Δxr、Δyr

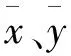
(2) 偏心畸变

镜头组件偏离主光轴的离心效果会导致偏心畸变，偏心畸变包含径向和切向两部分。二维像坐标下的偏心畸变表示为Δxd、Δyd

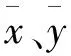
(3) 面外畸变

焦面的非平整性会导致面外误差，表示为Δru。二维坐标下的分量Δxu和Δyu表示为

(4)

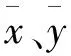
(4) 面内畸变

面内畸变Δrf的出现是由于胶片相机的胶面伸缩所致。CCD相机的伸缩影响是指x和y坐标间的不同尺度导致的伸缩比。为避免过度参数化，通常Δrf在二维坐标下建模为

式中，B1和B2称为仿射和裁切系数。该式顾及了像坐标轴间的尺度比例差异及非正交性。

Brown模型即是基于上述径向畸变和偏心畸变的数学形式建立的。如将式(5)加入到式(1)，即可得到近景数字相机检校中常用的10参数扩展模型[6]

2. 相关性分析与模型改进

近景相机自检校中主要关注3种强相关性：内部定向(IO)参数与外部定向(EO)参数间的强相关性；主点偏移和偏心畸变参数P1、P2间的强相关性； Δf和面内畸变参数B1间的强相关性。

第1种强相关性在长焦相机检校中影响较严重，在其他情况下，只要摄影配置得当，其影响很小[6]。第2、3种强相关性经常发生，所以这里重点分析。第2、3种强相关性其实是固有的，这主要是由Brown模型的多项式特性先天决定的。为了说明如何进行模型改进，这里以一个普通的二元多项式为例，取多项式前五项(忽略掉与相关性分析无关的常数项)为

为了最小化相关性，根据多项式逼近原理与Weierstrass定理[7]，如果要进行严格逼近，所有ΔxP中的参数都应与ΔyP中的参数相互独立，b1、b2、b4、b5应被a2、-a1、-a3、-a4相应地代替。强相关公式(7)则改化为如下的低相关公式

为了进一步描述正负号差异的影响，给出以下两组公式

类似参照式(8)，面内畸变应该写为

式(11)与式(5)处理缩放影响的效果十分类似，优点是在没有过度参数化的条件下使得B1和Δf之间的相关性大为降低。如图1所示，相比式(5)，式(11)更有利于和Δf的几何效果进行区分，这也直接导致式(11)中Δf和B1两参数间的相关性更小。

图1 (a)、(b)、(c)中的仿射参数B1>0时对应的几何影响效果

三、试验与结论

1. 试验数据集

由于希望避免其他误差对相关性分析的干扰，因此这里采用了模拟数据进行试验分析与验证。虚拟相机的焦距为8 mm，像面为7 mm×7 mm，像元大小为4 μm×4 μm，像点量测的高斯噪声标准差(std.dev)为0.1个像元。

试验中使用了两组模拟数据，分别包含10张、4张影像，如图2所示。在10张影像的摄影构形中，其中两张是俯视拍摄，其余8张是绕3D测试场每45°拍摄一张。这种高度冗余、高度可靠的摄影构形是按照文献[8]建议的摄影构形进行模拟摄影的。4张影像的摄影构形类似于文献[9]所采用的摄影构形，绕3D测试场每90°摄影一次。

图2 试验所用的摄影构形

2. 近景测量试验

近景试验目的主要是进行相关性分析并验证所提出偏心畸变及面内畸变改进模型的有效性。试验所用数据为上述的10张、4张两组模拟仿真影像。

(1)强相关性验证分析

对虚拟相机，设定Δx0、Δy0、Δf、K1非零，K2=K3=P1=P2=0。P1、P2为0意味着不存在标称偏心畸变，且可做到对式(3)、式(9)和式(10)的公平比较。自检校过程中会一并给出精确EO参数。Δx0和P1以及Δy0和P2的相关性系数见表1。

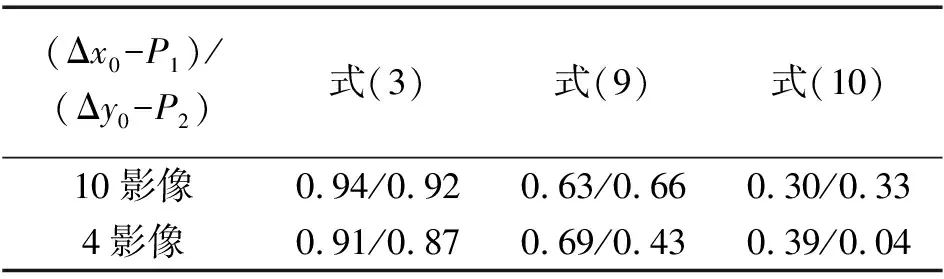
表1 像主点偏移和不同公式对应的离心畸变间的相关性

从表1可见，式(9)的相关性要比式(3)的相关性小得多,而与式(8)形式相近的式(10)在两个试验里相关性都最低。这一结果充分印证了前文的理论分析，即偏心畸变参数与主点之间存在强相关性，这主要是因为式(3)不像式(8)那样能有效地降低相关性，换言之，这些强相关性本质上是由于Brown模型中偏心畸变自身的多项式表述形式导致的。近景摄影相机定向(3个IO参数Δx0、Δy0、Δf乃至3个角元素ω、φ、κ的确定)中，若采用多项式自检校模型则会引起明显的强相关现象，且其几乎独立于摄影区域的摄影几何构形(即采用区域性特殊几何构型摄影无法消除其影响)。这些强相关性存在于自检校模型各项中，包括线性项x、y及xy中。只有遵从式(8)中的剔除规则，这种强相关性才有望避免。

(2) 像主点确定

由于Brown模型中偏心畸变是多项式表达形式，所以这种强相关性是必然存在的，因此有必要研究这种相关性对主点位置确定所造成的定量化影响。

设定虚拟相机的Δx0、Δy0、Δf、K1、P1、P2为非零标称值。考虑到偏心畸变量在像幅的边缘很少超过10 μm[10]，虚拟相机的偏心畸变设定为从1 μm递增到10 μm。

高度冗余的10影像摄影网络设计了两种检校策略：第一种策略是平差中仅使用Δx0、Δy0、Δf、K1参数；第二种策略是再追加式(3)中的P1、P2参数。策略一的主要目的是为了描述偏心畸变对主点位置确定所造成的影响；策略二更倾向于分析自检校中这两者的相互作用。

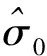
(12)

式中，ei为像点残差；N为多余观测数量(约束条件数减去未知数个数)。

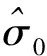
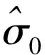
由于在诸多数字相机物镜中存在显著偏心畸变[7，11]，而且自检校中强相关性所产生的不良影响也是显著的，因此建议在自检校中尽量采用偏心畸变参数，这样不仅可以降低像点量测残差，而且可以提高主点位置的精度。

图3 未补偿偏心畸变下的检校结果变化情况

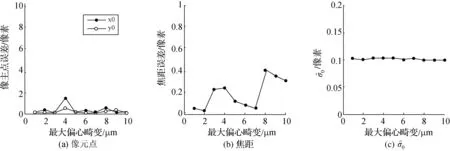
图4 不同偏心畸变下的检校结果变化情况

3. 结 论

从数学观点来看，由于多项式的各项之间存在强相关性，因此自检校模型采用代数多项式是不适宜的。尤其在近景摄影情况下，采用Brown模型必定会造成极强的相关性，从而给最终结果带来不确定性影响。这些在采用多项式自检校模型中必然固有的相关性是独立于区域性摄影几何构形的。用模拟试验对Brown模型的相关性进行了分析，验证了模型自身存在强相关特性，且这种强相关性会影响到主点标定的精度和可靠度，本文提出的面内畸变改进模型与焦距的相关性很低，从而对获得更好的检校结果十分有益。

参考文献：

[1] BROWN D. Close-range Camera Calibration [J]. Photogrammetric Engineering,1971,37(8): 855-866.

[2] KENEFICK J, GYER M, HARP, B. Analytical Self-calibration[J]. Ibid, 1972, 38(11):1117-1126.

[3] FAIG W. Calibration of Closerange Photogrammetry Systems: Mathematical Formulation [J]. PE&RS, 1975, 41(12):1479-1486.

[4] WONG W. Mathematical Formulation and Digital Analysis in Closerange Photogrammetry [J]. PE&RS, 1975,41(11):1355-1373.

[5] ZIEMANN H, HAKIM S. On the Definition of Lens Distortion Reference Data with Oddpower Polynomials [J]. International Archives of Photogrammetry, 1982， 24(1):123-130.

[6] MCGLONE J, MIKHAIL E, BETHEL J, et al. Manual of Photogrammetry[M]. Maryland: American Society for Photogrammetry and Remote Sensing, 2004.

[7] BROWN D. Decentering Distortion of Lenses [J]. Photogrammetric Engineering, 1966, 32(3): 444-462.

[8] WESTER-EBBINGHAUS W. Einzelstandpunkt-Selbstkalibrierung-ein Beitrag zur Feldkalibrie-rung von Aufnahmekammern[R]. Munich: Deutche Geodaetische Kommision (DGK), 1983.

[9] CLARKE T, WANG X, FRYER J. The Principal Point and CCD Cameras[J]. Photogrammetric Record,1998, 16(92):293-312.

[10] FRASER, C. Digital Camera Selfcalibration[J]. J.P&RS,1997, 52(4):149-159.

[11] ZIEMANN H. Thoughts on a Standard Algorithm for Camera Calibration [J]. IAPRS, 1986，26(5): 85-93.