通用线性模型在气象水文集合预报后处理中的应用

姜迪，智海，赵琳娜，段青云，梁莉，刘莹

(1．南京信息工程大学，江苏南京210044;2．中国气象科学研究院灾害天气国家重点实验室，北京100081;3．北京师范大学，北京100875;4．中国气象局 公共气象服务中心，北京100081;5．四川省气象台，四川 成都610072)

0 引言

洪水灾害是世界上危害最大、造成损失最多的自然灾害之一。但是由于其过程复杂，包含的不确定因素较多，目前的确定性预报对降水(气象)和流量(水文)的预报都难以满足实际需要，因此概率预报不失为一条提高水文预报精度的途径。采用概率预报的形式对水文不确定性进行定量描述，不仅可以提高预报的精度和可靠性，而且可以为决策者做出客观的最优决策提供更丰富的信息，同时也能满足用户对风险信息的需求。随着集合概率预报得到越来越广泛的使用，它有可能会取代单一预报(杜钧，2002;智协飞和陈雯，2010)。

本文的后处理是指在气象—水文集合预报系统中消除水文模型模拟过程产生的误差，降低水文模拟中不确定性影响的过程。水文后处理方面的研究以贝叶斯方法取得的成果较为突出。Krzysztofowicz(1985)首先提出了基于正态线性假设的贝叶斯预报处理器(Bayesian Processor of Forecasts，简称BPF)，通过贝叶斯公式求得待预报流量的后验分布，并基于后验分布提出最优决策。随后，Krzysztofowicz(1999)又提出了基于贝叶斯理论框架的水文预报系统(Bayesian Forecasting System，简称BFS)，将降水预报不确定性与水文模型不确定性分别量化，然后通过全概率公式将二者耦合起来，得到水文预报不确定性的解析解，BFS可以与任何模型或预报方案相结合使用。之后Krzysztofowicz and Kelly(2000)在BPF的基础上提出了水文不确定性处理器(Hydrologic Uncertainty Processor，简称 HUP)，HUP的核心是亚高斯模型，对实测值和预报流量进行正态分位数转化(使得转化变量的线性正态关系更加显著)，由贝叶斯公式得到转化变量的后验密度函数，然后还原得到待预报流量的后验密度函数。Krzysztofowicz and Maranzano(2004)还提出了一种基于HUP方法产生的概率水位预报来消除误差。基于这种方法，Seo et al．(2006)为美国国家气象局的河流预报系统提供了一种水文后处理器。国内对水文预报的不确定性也做了很多探索，王善序(2001)、钱明开等(2004)、张洪刚和郭生练(2004)、张洪刚等(2004)、梁忠民等(2010)利用 BFS、HUP等方法进行了水文不确定性和概率水文预报的研究，结果表明，概率预报与确定性预报同样有价值，特别是当预报不确定性比较大时，概率预报比确定性预报在决策方面具有更高的经济价值。贝叶斯方法在气象集合预报中也有诸多应用，陈法敬等(2011)及段明铿和王盘兴(2006)利用贝叶斯方法提高了集合预报系统的性能，提高了预报精度。另外，还有一些其他研究方法，如:Georgakakos and Smith(1990)利用卡尔曼滤波技术与水文模型相结合，得到模拟流量的均值与方差，进行短期洪水预报;Georgakakos et al．(1998)通过蒙特卡洛法随机生成若干组不同代表类型的气象资料，以不同的初始条件输入水文气象模型中得到所有可能的径流过程，延长了预见期，提高了模拟的可见性。

但是上述方法都有各自的缺陷，例如贝叶斯方法需要知道不确定性的概率分布和协方差结构，卡尔曼滤波方法无法输出不确定性的解析解，蒙特卡洛方法在随机抽取样本方面收敛速度慢，精确度不高，对于三维以下的问题不如基于线性最小二乘回归的自适应方法、分对数回归模型的自适应算法和卡尔曼滤波方法好(冯圆和龚晓燕，2010)。而通用线性模型(General Linear Model，简称GLM)方法可以避开这些问题，得到比较可靠的概率水文预报。

1 通用线性模型方法

从概率上看，水文后处理过程实际上是要得到一个条件概率密度函数，这个条件概率密度函数是f(yobs|yfcst)，即给定了气象预报yfcst的观测值yobs条件概率密度函数。如果忽略其他原因产生的误差，

只关注于模型模拟水文事件产生的误差，通用线性模型后处理方法的原理可以用方程(1)表示:

图1是一个GLM的数据窗口示意图。根据Zhao et al．(2011)对通用线性模型方法的研究，数据窗口主要分为分析期和预报期。分析期的作用是提取资料样本以确定GLM模型参数，然后使用确定好的GLM模型对预报期的资料进行校正，得到校正过的预报值。Na和Nf分别代表分析期和预报期的长度。在分析期和预报期的前后各有一个buffer期，作用是增加参与确定GLM模型参数的样本数量，更好地确定 GLM模型参数。Nbuffer表示buffer期的长度。

如果随机变量yobs(观测值)、ysim(模拟值)和yfcst(预报值)是服从正态分布的，就可以利用通用线性模型方法去解决方程(1)的问题(R and Schakke，1973)。

图1 通用线性模型的数据窗口示意图Fig．1 Sketch map of data window of GLM

由于上述方法要求Z1和Z2中的变量服从正态分布，显然观测和模拟流量并不满足这一条件，所以本文使用由Krzysztofowicz(1985)提出的正态分位数转换方法(Normal Quantile Transformation，简称NQT)来解决这一问题。这种方法是将原始空间中的流量数据转换为在转换空间中的正态分布变量，使转化变量的线性正态关系更加显著。随后进行一个逆NQT过程，将转换变量的估计值转换回原始空间才能使用并符合正态分布的数据。

2 数据与试验介绍

本文使用的数据来自国际模型参数估计试验(ModelParameterEstimationExperiment，简 称MOPEX)(Duan et al．，2005)。MOPEX 是一个关于水文模型和大气模式的陆面参数化方案的国际合作项目，得到了世界气象组织(WMO)、国际水文科学协会(简称IAHS)等多个气象、水文部门和科学组织的支持。它通过利用气象资料和水文资料对大量水文模型在相当数量的河流流域里进行模型参数的率定试验，以探索模型最优参数的估计方法。入选MOPEX的流域无大型水利工程，受人工影响较少，可以反映天然状况下的水文过程。美国本土与中国纬度相近，有多种相似的气候类型，尤其是密西西比河流域与中国长江流域有很多共同点，可以为中国的水文研究提供参考。

MOPEX中水文模型输出的模拟数据分为两种，一种为经过模型参数率定的水文模型产生的模拟数据(简称CAL数据)，其模拟误差较小;另一种为未经过参数率定的水文模型产生的模拟数据(简称APR数据)，其模拟误差较大。

本文选取MOPEX数据库中French Broad River流域作为试验流域。此流域面积为2 448 km2，此区域73%的覆盖面积为森林，年降水量为1 676 mm。同时选取萨克拉门托水文模型(Sacramento，简称SAC模型)作为试验模型，数据的时间长度为36 a，即1962年1月1日至1997年12月31日。SAC模型最早是一个设计用于洪水预报的概念性的集总式模型。它包括16个参数，利用一系列有一定物理概念的数学公式来描述水分的运动过程，具有较强的物理概念和广泛的适用性(刘金平和乐嘉祥，1996)。目前SAC模型在美国被广泛应用于水文预报，同时也是中国国内引入较早、研究应用比较多的水文模型。

确定了模型和流域后，本文将根据不同的试验设计选取分析期资料确定GLM模型参数，然后用确定好参数的GLM模型去校正预报期的流量模拟值并产生关于预报期的集合预报，依据对不同误差水平的两种资料(APR资料和CAL资料)的后处理效果来检验GLM校正误差的能力:1)使用GLM分别对两种模拟数据进行校正，分析期和预报期均与资料时间长度相同，通过若干统计指标将校正结果与实际观测对比，检验误差校正效果;2)GLM使用不同的校验策略，即使用不同年代长度的分析期资料来确定GLM模型参数，然后对预报期的模拟资料进行后处理，测试在使用不同数量样本确定的模型参数下GLM校正误差的能力。

3 结果分析

3.1 两种数据集GLM在不同误差水平下的误差校正能力

试验中，设定数据窗的参数为:Na取30 d，Nf取30 d，Nbuffer取30 d;预报起始日期为2月24日。试验选用36 a资料确定GLM模型参数，并用36 a资料进行验证。

首先，根据第2节所述，需对数据进行NQT转换，使其符合正态分布。图2为APR数据和CAL数据在NQT转换前后与实际观测的相关系数比较。可见，在进行NQT转换前，CAL数据与实际观测的相关系数基本达0.8，而APR数据与实际观测的相关系数为0.6～0.8，CAL数据的相关性明显好于APR数据。经NQT转换后，两数据与实际观测的相关系数均有提高，CAL数据的相关系数为0.8～0.9(达0.9的数据明显较多)，仍然好于APR数据(仅个别数据的相关系数达0.9)。

图3是使用CAL资料和APR资料产生的集合流量预报的连续等级概率评分(Continuous Rank Probability Score，简称CRPS)的比较。CRPS的值可以定量地评价集合预报的性能;值越大表示集合预报的性能越差，值越小表示集合预报越好，零分代表最好预报。由图3可见，两种资料产生的集合流量预报的CRPS值在整个预报期内都处于较低水平，使用APR资料的集合预报的CRPS值全部低于0.45，而使用CAL资料的集合预报的CRPS值都低于0.4，说明GLM后处理器产生的集合流量预报是较可靠的。使用两种资料的集合预报在预报期的初始阶段均较好，得到了很低的CRPS值，随着预报时效延长，CRPS值逐渐升高，说明预报效果不断变差，这也是符合预报的一般规律的。整体而言，可以认为整个预报期内的集合预报效果是可靠的。

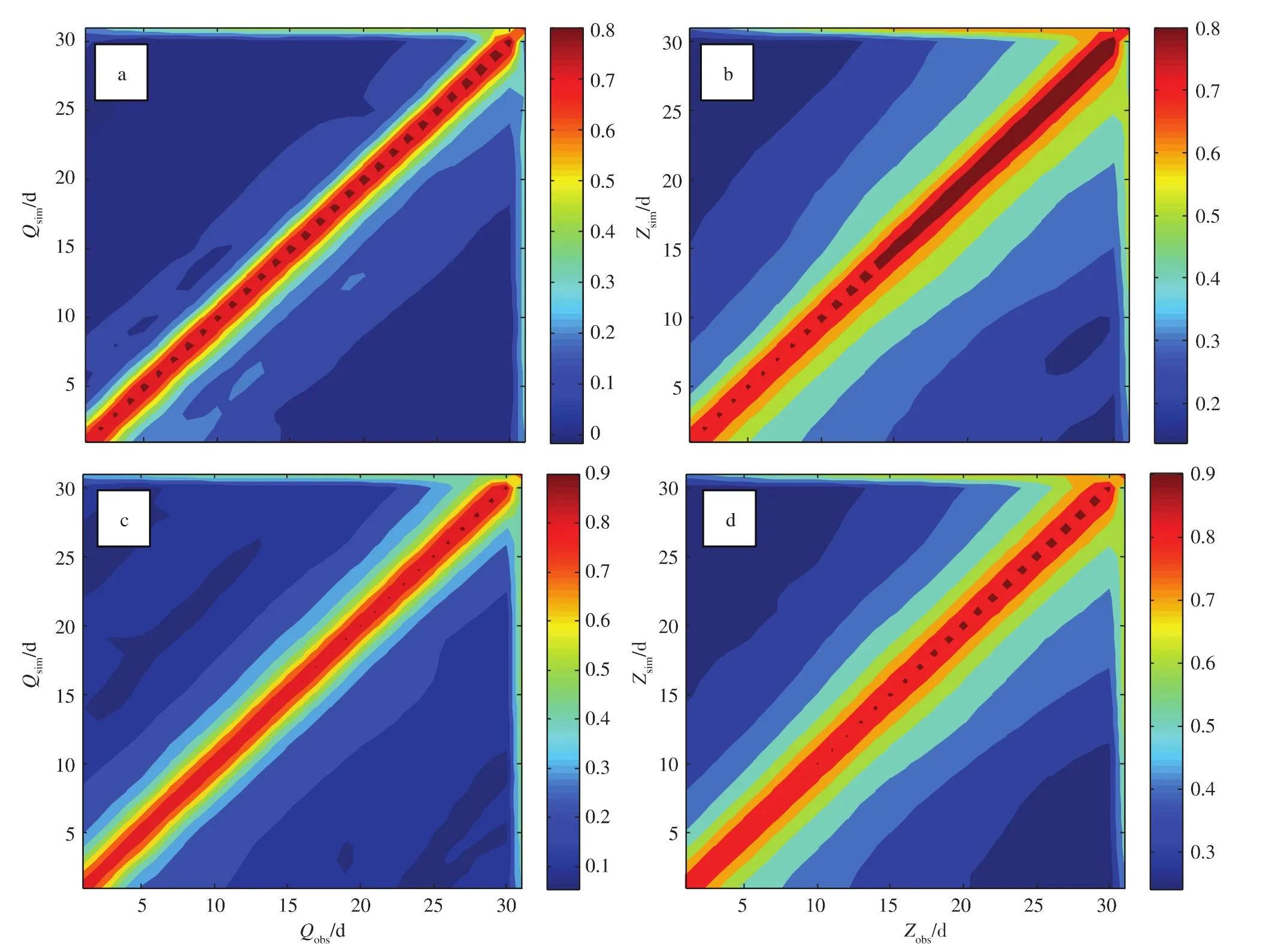
图2 NQT转换前后原始预报与实际观测的相关系数 a．APR资料转换前;b．APR资料转换后;c．CAL资料转换前;d．CAL资料转换后Fig．2 Correlation coefficients between raw simulations and observations(before or after NQT transformation) a．APR data before NQT transformation;b．APR data after NQT transformation;c．CAL data before NQT transformation;d．CAL after NQT transformation

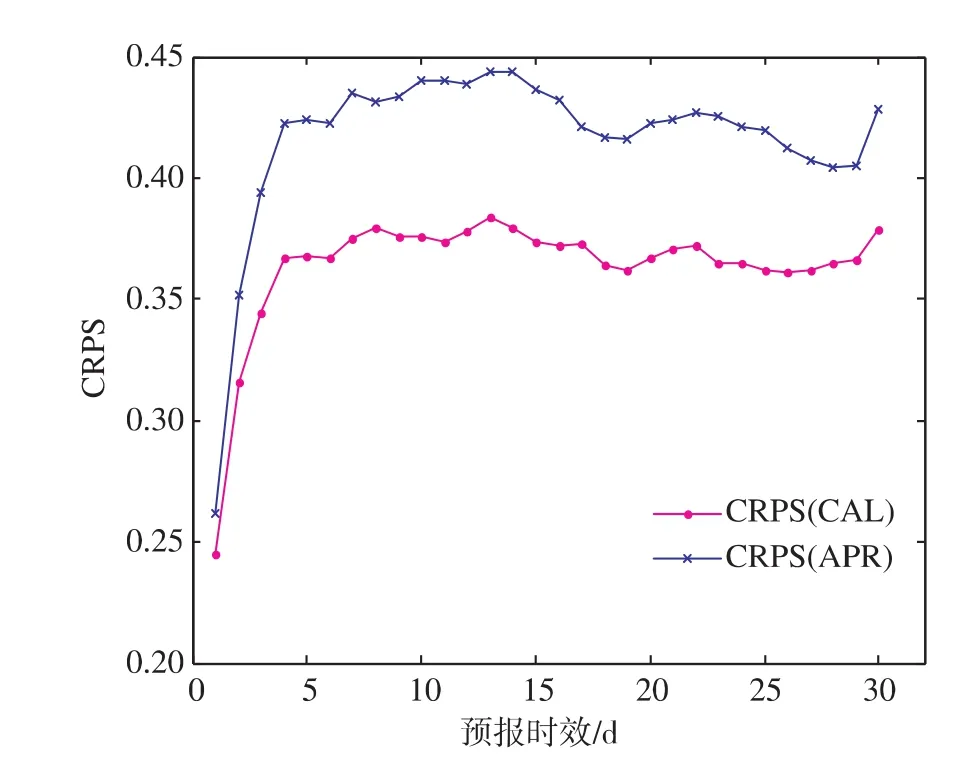
图3 使用APR和CAL资料的集合预报的CRPS比较Fig．3 Comparison of CRPS scores from ensemble forecasts using APR and CAL data

图4是GLM使用两种资料的校正结果与实际观测在统计指标上的对比。在下面的对比中选用集合预报结果的集合平均作为单值的校正预报，这是因为集合平均位于集合中位与预报分布的中心，代表了真实情况下最有可能出现的状况。

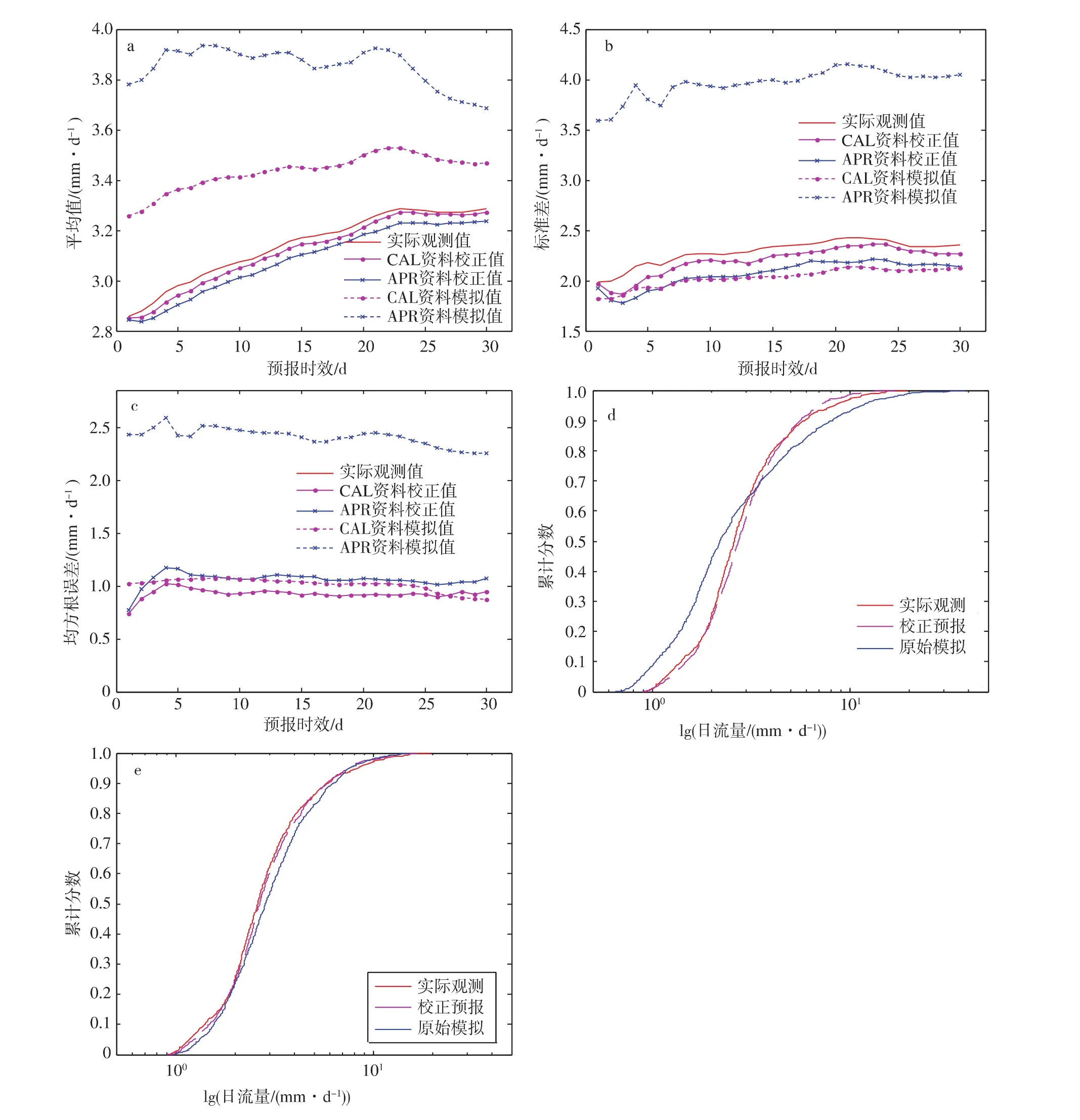
图4 使用不同资料水文模拟结果的评估 a．原始模拟、校正值与实际观测的平均值对比;b．原始模拟、校正值与实际观测的标准差对比;c．原始模拟和校正值的均方根误差对比;d．APR资料的原始模拟、校正值与实际观测的累积分布函数比较;e．CAL资料的原始模拟、校正值与实际观测的累积分布函数比较Fig．4 Evaluations of results using different simulation data a．comparison of mean of raw simulation，adjusted and observation;b．comparison of STD of raw simulation，adjusted and observation;c．comparison of RMSE of raw simulation and adjusted;d．comparison of CDF of raw simulation，adjusted and observation using APR data;e．comparison of CDF of raw simulation，adjusted and observation using CAL data

图4a是使用CAL资料和APR资料的原始模拟值、校正预报值与实际观测三者平均值(简称Mean)的比较。校正预报的流量是否与实际观测相吻合是对校正效果好坏最直观的判断。图4a表明，不论使用APR资料还是使用CAL资料，预报期内校正预报的平均都比原始模拟的平均更加接近于实际观测平均。这表明经过GLM后处理器的处理，有误差的水文模拟得到了很好的校正，结果更接近实际观测。对APR资料和CAL资料的校正结果进行对比可知，误差较小的CAL资料的校正结果相对于误差较大的APR资料的校正结果更接近实际观测，说明GLM不仅可以处理误差较大的水文模拟，对于误差较小的水文模拟也有一定的处理能力。

图4b是使用CAL资料和APR资料的原始模拟值、校正预报值与实际观测三者的标准差(Standard Deviation，简称STD)的比较。STD是对不确定性的一种量化。STD越高，表示试验数据越离散，即观测值与预测值相差越大;反之，STD越低，则代表观测值与预测值相差越小。图4b表明，不论是使用APR资料还是使用CAL资料的结果，经过GLM后处理的校正预报的标准差都比原始模拟更接近于实际观测，尤其是对APR资料的改善极其显著。其中尽管APR资料的校正结果的STD相比于CAL资料的校正结果的STD得到了较大程度的校正，更接近于实际观测，但由于被校正得过低，反而与真实情况有差距。对比CAL资料的标准差的校正情况，可以认为APR资料经过GLM校正后，还包含了较大的不确定性，这些不确定性可能与水文模型自身的参数率定有关。

图4c是使用CAL资料和APR资料的校正预报值与原始模拟值的均方根误差(Root-Mean-Square Error，简称RMSE)的比较。RMSE是由实际观测值与预报值之间的差值定义的，RMSE的值越大，表示预报误差越大，反之则表明预报误差越小。可以看到，相对于原始预报的RMSE，经过后处理的校正预报的RMSE明显降低。使用APR资料的校正预报的误差被降低到使用CAL资料的原始预报的误差几乎同样水平，而CAL资料的校正预报的误差则得到了更进一步降低，这也验证了之前分析的结论。

图4d和图4e分别是APR资料和CAL资料的原始模拟、校正预报与实际观测的累积分布函数的比较。累积分布函数(Cumulative Distribution Function，简称CDF)描述的实数随机变量x的概率分布，也是概率密度函数(Probability Density Function，简称PDF)的积分。概率密度函数表示的是随机变量的瞬时取值落在某指定范围内的概率，CDF代表的是随机变量x小于或者等于某个数值的概率，也就是连续函数F(x)的分布。图4d和图4e表明，APR资料和CAL资料经过GLM处理的校正值在分布上都更接近实际观测;特别是CAL资料，经过水文模型自身的参数率定之后，其误差已得到较大程度的降低，数据分布与实际观测数据相当接近，再经过GLM后处理后，数据分布状况得到进一步改善。

综合所述，这些试验初步证明GLM不仅可以有效降低水文模拟中的误差，还可以产生可靠的集合流量预报。它不仅对误差较大的水文模拟能取得较好的校正效果，而且对误差较小的水文模拟也有一定的处理能力，可以进一步降低误差。

3.2 不同的校验策略下GLM的性能比较

在下面的试验中，数据窗口的参数不变，只是选取了另外两种不同的校验GLM模型参数的策略(即选择不同年代长度的分析期和验证期资料)，来进行与第3.1节一样的试验，以测试GLM在不同校验策略下的校正效果。

由表1可见，校验期策略1(即第3.1节使用的试验设计)表示用36 a长度的资料确定GLM模型参数，然后用同样的36 a资料进行验证;校验期策略2表示用前18 a资料确定GLM模型参数，用后18 a资料进行验证;校验期策略3表示用单数年(共18 a)资料确定GLM模型参数，用偶数年(共18 a)资料进行验证。

图5a、图6a分别是在使用校验策略2、3情况下用不同资料得到的模拟值、校正值与实际观测平均值的比较。可见，不管使用哪种校验策略，经过GLM处理的校正值都比原始模拟值要更加接近实际观测，误差得到有效降低。而且使用CAL资料的校正值在两个统计指标上也都比使用APR资料的校正值更加接近实际观测，其他指标如标准差、累积分布函数等的结果也大致相同，不再赘述。该结果既支持了上一个试验所得到的结论，又说明GLM后处理器在不同校验策略下(即在不同的参数配置下)，对水文模拟中不确定性的校正作用也是有效的。

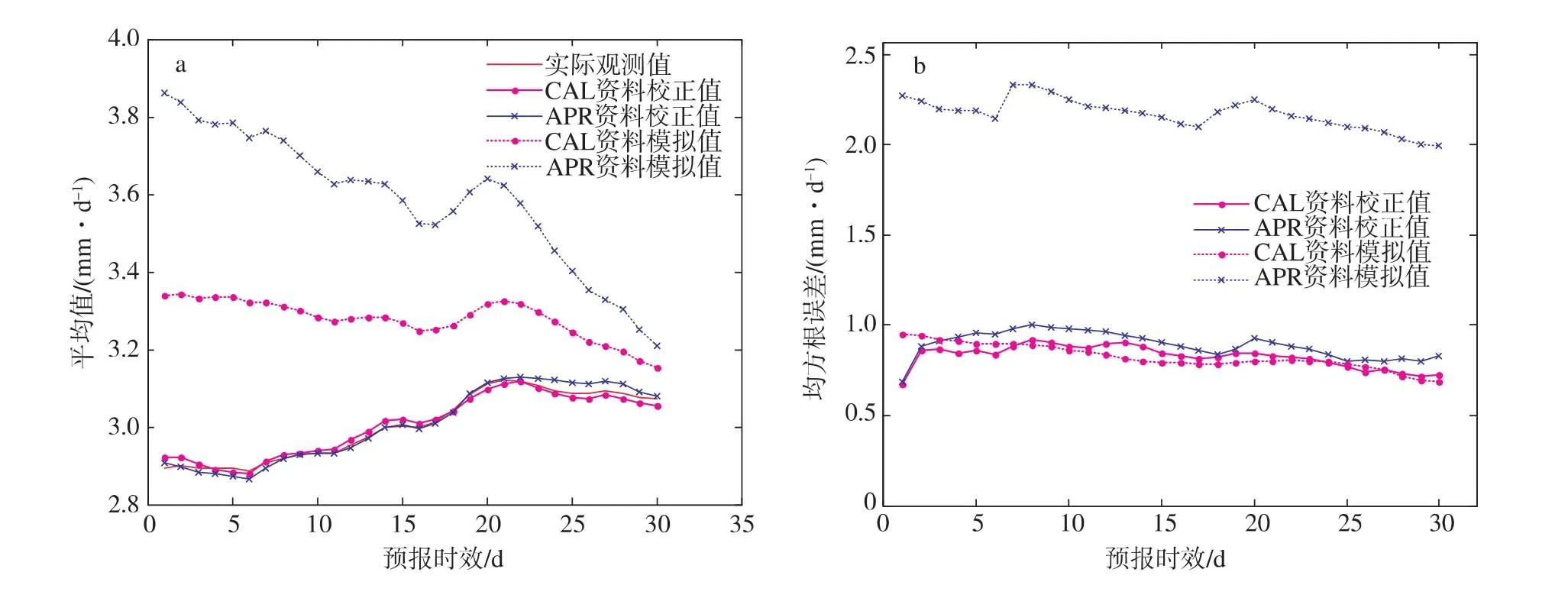
图5 校验策略2的结果 a．原始模拟、校正值与实际观测的平均值对比;b．原始模拟和校正值的均方根误差对比Fig．5 Results of the calibration strategy 2 a．comparison of mean of raw simulation，adjusted and observation;b．comparison of RMSE of raw simulation and adjusted

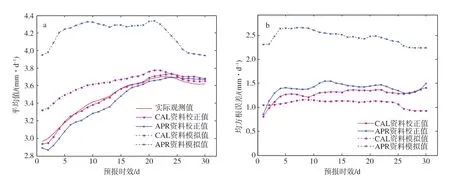
图6 校验策略3的结果 a．原始模拟、校正值与实际观测的平均值对比;b．原始模拟和校正值的均方根误差对比Fig．6 Results of the calibration strategy 3 a．comparison of mean of raw simulation，adjusted and observation;b．comparison of RMSE of raw simulation and adjusted

但是，也应注意到，在预报的某些时段内，使用CAL资料的校正预报误差并不比使用APR资料的校正预报误差更低(图5b、图6b)，这表明并不是所有的有误差的水文模拟通过GLM后处理都能得到改善。其原因在于:如果对降水资料的前处理以及水文模型自身的参数率定等前期工作可以得到比较理想的结果，使得水文模拟中的误差已经消除得比较多，则后处理过程无法再进一步减小误差。

由于3种校验策略的本质区别是参与确定GLM模型参数的样本数量不同，可以看到使用策略1的样本数量最多，使得使用策略1得到的校正效果最好，所以参与确定GLM模型参数的样本值越多，提取的历史信息越多，校正的结果就越接近实际观测。

4 结论

本文利用MOPEX提供的两种不同误差水平的资料，对比检验GLM后处理器对水文集合预报误差的校正能力。结果如下:

1)GLM后处理器可以产生可靠的水文集合预报，集合预报的连续分级概率评分值都在比较低的水平，证明预报结果是可靠的。

2)GLM后处理器对有偏差的水文预报的校正效果是显著的。在平均值、标准差、均方根误差等统计指标方面的比较显示，无论是误差较大或者是误差较小的水文模拟，校正预报都要比原始模拟更加接近于实际观测，误差显著降低。

3)即使是对经过参数率定的水文模型产生的误差较小的水文模拟，GLM后处理器仍然有能力消除一部分误差。

4)使用不同的校验策略，选取不同的分析期资料对不同预报期资料进行校正，GLM后处理器都能很好地反映出实际观测的变化趋势，降低原始模拟中的误差。这表明GLM的处理效果是稳定有效的，不会因为较少的资料而造成误差校正效果的显著下降。

5)通过试验结果对比，发现当原始模拟已经做得足够好，模拟误差已经比较小的时候，后处理不一定能得到更好的结果。

本文只选取了MOPEX数据库中一个模型在一个流域上的资料进行试验，初步验证了GLM的性能。下一步要扩大流域和模型的数量，特别是加强国内流域和水文模型的试验，以进一步证明GLM的校正能力是普遍有效的。

陈法敬，矫梅燕，陈静．2011．一种温度集合预报产品释用方法的初步研究［J］．气象，37(1):14-20．

杜钧．2002．集合预报的现状和前景［J］．应用气象学报，13(1):16-28．

段明铿，王盘兴．2006．一种新的集合预报权重平均方法［J］．应用气象学报，17(4):488-493．

冯圆，龚晓燕．2010．基于蒙特卡罗方法的气象问题应用研究［C］//第27届中国气象学会年会大气物理学与大气环境分会场论文集．北京:中国气象学会．

梁忠民，戴荣，王军，等．2010．基于贝叶斯模型平均理论的水文模型合成预报研究［J］．水力发电学报，29(2):114-118．

刘金平，乐嘉祥．1996．萨克拉门托模型参数初值分析方法研究［J］．水科学进展，3(7):252-259．

钱名开，徐时进，王善序，等．2004．淮河息县站概率预报模型研究［J］．水文，24(2):23-25．

王善序．2001．贝叶斯概率水文预报简介［J］．水文，21(5):33-34．

张洪刚，郭生练．2004．贝叶斯概率洪水预报系统［J］．科学技术与工程，4(2):74-75．

张洪刚，郭生练，刘攀，等．2004．基于贝叶斯分析的概率洪水预报模型研究［J］．水电能源科学，22(1):22-25．

智协飞，陈雯．2010．THORPEX国际科学研究新进展［J］．大气科学学报，33(4):504-511．

Duan Q，Schaake J，Andreassian V，et al．2005．Model parameter estimation experiment(MOPEX):Overview and summary of the second and third workshop results［J］．J Hydrol，320(1/2):3-17．

Georgakaos K P，Smith G F．1990．On improved hydrologic forecasting—Results from a WMO real-time forecasting experiment［J］．J Hydrol，114(1):17-45．

Georgakakos A P，Yao H，Mullusky M G，et al．1998．Impacts of climate variability on the operational forecast and management of the upper Des Moines River basin［J］．Water Resour Res，34(4):799-821．

Krzysztofowicz R．1985．Bayesian model of forecasted time series［J］．Water Resour Res，21(5):805-814

Krzysztofowicz R．1999．Bayesian theory of probabilistic forecasting via deterministic hydrologic model［J］．Water Resour Res，35(9):2739-2750．

Krzysztofowicz R，Kelly K S．2000．Hydrologic uncertainty processor for probabilistic river stage forecasting［J］．Water Resour Res，36(11):3265-3277．

Krzysztofowicz R，Maranzano C J．2004．Hydrologic uncertainty processor for probabilistic stage transition forecasting［J］．J Hydrol，293(1):57-73．

Seo D J，Herr H D，Schaake J C．2006．A statistical post-processor for accounting of hydrologic uncertainty in short-range ensemble streamflow prediction［J］．Hydrology and Earth System Sciences Discussions，3(4):1987-2035．

R D V，Schakke J C Jr．1973．Disaggregation processes in stochastic hydrology［J］．Water Resour Res，9(3):580-585．

Zhao L，Duan Q，Schaake J，et al．2011．A hydrologic post-processor for ensemble streamflow predictions［J］．Adv Geosci，29:51-59．