GPS导航系统下坐标转换及应用＊

谭宝成，邓子豪

（西安工业大学 电子信息工程学院，西安 710021）

近年来，GPS技术以其快速、精确、全天候在测量中的应用变的越来越广泛，GPS和电子地图相结合构成的实时监控系统得到广泛使用.在实际工程中，车辆在电子地图上显示有误差，坐标转换产生的误差就是其中一种，因此如何减少转换过程中的误差成为现今研究的热点.文献［1］介绍空间七参数转换模型求解方法及对误差进行分析，并将该方法应用在大地测量当中，在转换过程中，当变换参数较少，利用其他点进行位置修正，求出的转换参数具有区域性和时间性，但没有讨论监测点位置分布对大地测量精度的影响.文献［2］从GPS接收机自身存在干扰和噪声入手，通过研究GPS接收机抗干扰性的算法，获取最大输出信噪比，提高GPS接收数据稳定性，从而改善GPS导航系统的定位精度.文献［3］通过对转换模型三参数和七参数进行实际的应用，表明两种算法适用的区域范围，有助于了解转换模型的适用特点.文献［4］主要通过研究GPS／GLONASS组合定位时来提高GPS导航定位精度，采用Helmert方差分量估计确定两类观测值的权比，其组合静态定位较单一系统解算的基线精度均有提高，在山区和有障碍物遮挡地方，导航静态定位精度和可靠性比较高，但算法复杂，实时性较差，动态定位精度较低.文献［5］提出二维七参数和三参数模型，分析了公共点密度对不同坐标模型转换精度的影响，研究这两种模型的外推范围和外推误差大小，为不同大小区域坐标系之间选择合适的转换模型提供重要的参考.文献［6］提出了四参数转换算法在导航定位中的应用，详细的推导转换模型的实用公式，提出新的残差内插法，有效剔除误差较大公共点，与传统算法相比转换参数较少，算法简单，适用于中小城市测量.

文中分析讨论七参数转换模型，将其应用到GPS导航定位中，实现 WGS－84地心坐标系下的点转换为北京54大地坐标系的点，通过投影变换转换到实际平面坐标上，强调了公共点存在原始误差，并分析公共点的分布位置和密度对坐标转换精度的影响.

1 WGS－84和北京54坐标系

1.1 WGS－84坐标系

WGS－84大地坐标系是一个地心坐标系，其定义及所采用的椭球参数为：坐标系的原点在地球质心；Z 轴指向BIH1984.0，定义的协议地球极（CTP）方向为X轴指向BIH1984.0的零度子午面与CTP赤道的交点；X轴与Z轴构成右手系，其长半轴a＝6378137，短半轴b＝6356752.314，扁率为298.3［4］.

1.2 北京54坐标系

北京54坐标系为参心大地坐标系，大地上的一点可用经度L54、纬度 M54和大地高H54定位，其是以克拉索夫斯基椭球为基础，经局部平差后产生坐标系，1954年北京坐标系可认为是前苏联1942年坐标系的延伸，其中长半轴a＝6378245，短半轴 b＝6356863.018，扁率为 298.3［7］.

克氏椭球与 WGS－84椭球的长半轴相差108m，短半轴相差107.705m，两个差值并不相等，即在GPS接收到的点（WGS－84坐标系统的）叠加到北京54坐标系统的底图上，可发现这些GPS接收点与实际地点发生了位置上的偏差.因此要把GPS点从WGS－84的坐标系统转换成北京54的坐标系统，这两个坐标系椭球体相对关系［8-10］如图1所示.

图1 北京54空间坐标系和WGS－84空间坐标系的相对关系Fig.1 Relative relationship between Beijing 54 and WGS－84coordinate systems

2 WGS－84和北京54坐标系转换

2.1 七参数的转换模型

为了把车载GPS接收机中接收的WGS－84坐标转换为电子地图使用的北京54坐标，文中采用七参数坐标转换，当解算出转换参数才能进行坐标之间的转换，由于每个固定区域范围内的坐标参数不同，因此一个国家内使用一个转换参数会带来极大的误差，为了保证转换精度，文中选取某一地区作为测试区来验证坐标转换模型的精度，且对影响坐标转换精度的主要因素进行研究讨论.

WGS－84坐标与北京54坐标的坐标变换步骤［5］为

① 同一基准下空间大地坐标转换成空间直角坐标系；

② 根据所采用的七参数变换方法求解出转换参数；

③ 按照所求参数把待定点带入到转换模型中进行求解；

④将转换得到的北京54空间直角坐标通过高斯投影变为平面坐标.

2.2 高斯投影正算的简化公式

将同时具有WGS－84坐标和北京54坐标的3个或3个以上的控制点代入布尔沙公式中可以求出坐标转换所需要的7个参数，即求3个平移参数，1个尺度因子，3个旋转参数.

布尔沙七参数转换模型的变换公式［2］为

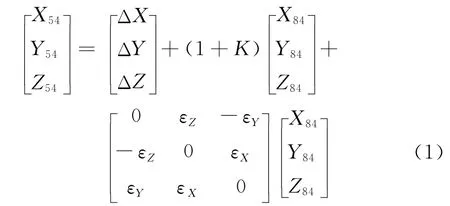
式中：ΔX，ΔY，ΔZ 为平移转换参数；εX，εY，εZ为旋转参数；K为比例因子.式（1）共7个参数，即为七参数法，是一种相对精准的转换模型.

图2 坐标转换流程图Fig.2 Flow chart of coordinate transformation

式（2）可简写为

X54＝X84＋CiR

现测定已知3个点，i＝1，2，3.

则可以根据最小二乘法解R，方法为

建立方程组

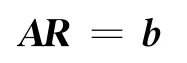
可求R时，将（AR－b）T（AR－b）取最小值，把变量的纯量函数去极值化定义化为

解方程为

解得R，求得7个转换参数.

2.3 高斯投影正算的简化公式

将GPS所接收到的定位数据空间大地坐标（L，B）转换为高斯平面坐标，其所依据的数学法则方程式［5］为

确定式（3）的具体形式，需要根据高斯投影的特殊条件才能导出高斯投影的计算公式.高斯投影必须满足以下三个条件：

1）中央子午线投影后为直线；

2）中央子午线投影后长度不变；

3）投影具有正形性质，满足正形投影条件.

式（3）中，L，B为椭球面上的某点的大地坐标；x，y为某点投影后的平面直角坐标，根据其推导出的正算公式为［3］

根据GPS车载导航的实际精度要求，忽略x等式的6次以上的高阶项以及y等式7次高阶项，得到实用公式为

式中：X为自赤道量起的等量纬度为q的中央子午线弧长；l＝ （L－L0）／2；L0为投影带中央子午线经度；ρ＝206265；a、b分别为参考椭球的长、半径卯酉圈曲率半径N＝a／；椭球的心率e＝2α－α2.

为了比较式（4）和式（5）在转换精度的差别，文中采用某局部地区的100个WGS-84坐标下的点进行比较，分别计算出简化公式与高次公式在x方向上的差值，和在y方向上差值，并对计算结果进行比较，x和y的误差在厘米级别，能满足GPS车载导航的定位精度，其统计结果见表1.

表1 实用高斯正算公式的精度分析表Tab.1 Precision analysis with Gaussian calculate formula

3 公共点影响坐标转换精度的结果及分析

文中实验数据来自于西安市某区域的GPS的C级，由37个点组成，其中有15个国家一级三角点，根据实验区域和分布情况选择其中的12个三角点为公共点作为实验数据，并采用该分布均匀5个点作为覆盖网的公共点，其最远两点相距约25 km，最近两点相距3km，公共点分布如图3所示，试验时，试验公共点同时具有北京54和WGS－84两套空间直角坐标，将 WGS－84坐标转换成相应的北京54空间直角坐标，选取5个点进行坐标系统转换求参，选取另一部分点作为转换点.将转换点的WGS－84坐标转换到BJ54空间直角坐标系统中，比较转换坐标和原坐标之间的偏差，由于一般GPS的定位偏差在2～3m.因此坐标转换偏差小于0.5m时，满足GPS定位精度要求.

3.1 公共点的分布对坐标转换精度的影响

已知12个公共点的 WGS－84坐标（B54，L54）和北京54平面坐标（X54，Y54），将12个公共控制点显示在一个规定大小的范围内，如图3所示，为了验证公共点分布对转换精度的影响，从中选取5个点作为测试区域的公共点.

图3 公共点位分布图Fig.3 Distribution of public points

选取公共点有两种方案：①把G5，G6，G1，G8，G11这5个点作为公共点，求转换七参数，通过坐标转换把WGS－84系下的7个点作为待测点，转换到北京54平面坐标系下的坐标值，与原北京54坐标值相比较，结果见表2.从表2可知X的坐标残差平均值精度较高，Y方向的坐标残差坐标平均值较大，尤其是G3点坐标残差较大，因此用三个分布范围较小的点作为公共控制点不能满足实际要求.

② 采用G5，G6，G1，G3，G4这5个点作为公共点，由图2可以看出，这5个点构成的覆盖范围最大，且能把7个点全部覆盖.按照方案①步骤进行计算，将计算出的这7个待测点坐标和原北京54坐标值列于表3.

方案1中公共点分布紧密覆盖范围较小，利用七参数转换模型求出的坐标值精度不能满足车体定位精度.而方案2中覆盖整个区域的5个点作为公共控制点时，3个点组成三角形边长最长，其6个点坐标残差较小，坐标值精度较高，结果表明七参数坐标转换在一定区域内具有一定的外推性.

3.2 公共点密度对坐标转换精度的影响

为了研究公共点的密度对待转换点精度的影响，把G7、G8作为待转换点，使用5种分析方案：①采用G2、G3、G5号点作为公共点；②采用G2、G3、G9、G5号点作为公共点；③采用 G1、G2、G3、G9、G5号点作为公共点；④采用G12、G1、G2、G3、G9、G5号点作为公共点；⑤G6、G12、G1、G2、G3、G9、G5号点作为公共点.把G7和G8的偏差平均值列于表4中，由表4可以看出，方案3的转换精度最高，转换精度并不随公共点数的增加而增加，而是先变大后变小的趋势，研究表明，只有当公共点数量合适时，其待转换点的精度才能达到最高，在小范围内待测点的数量不能太多，以避免公共点自身随机误差的影响.

表2 转换后的WGS－84坐标值与原北京54坐标值的比较Tab.2 The transformed WGS －84coordinates compared with the original Beijing 54values

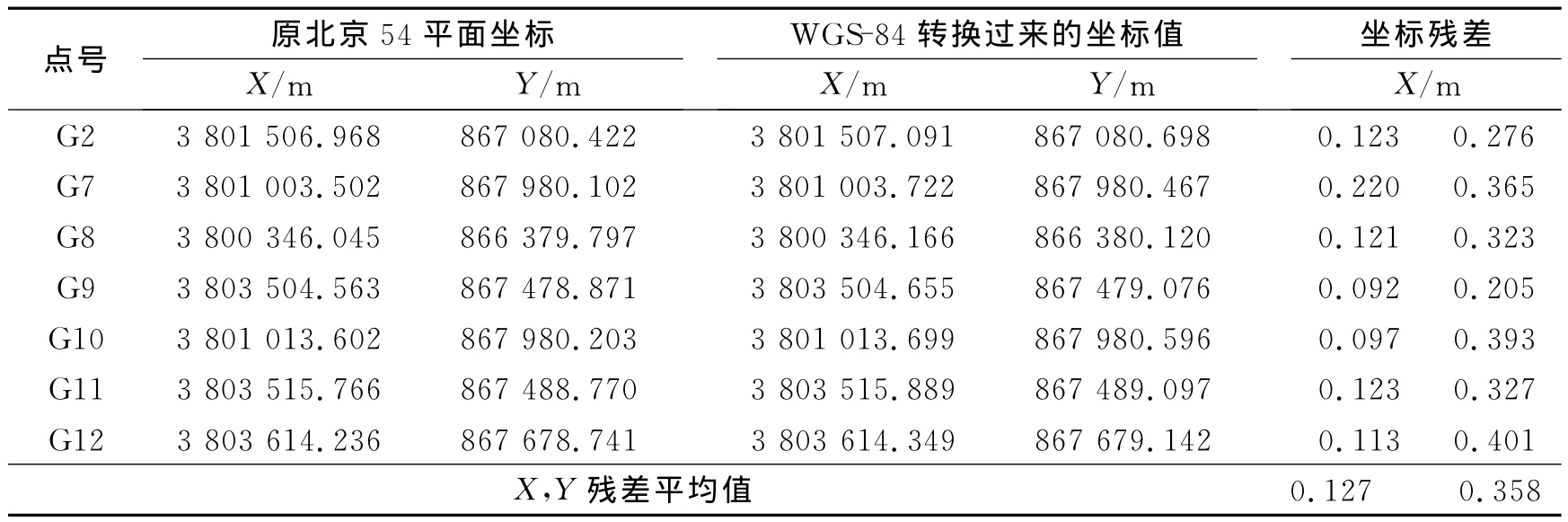
表3 转换后的WGS－84坐标值与原北京54坐标值的比较Tab.3 The transformed WGS －84coordinates compared with the original Beijing 54values

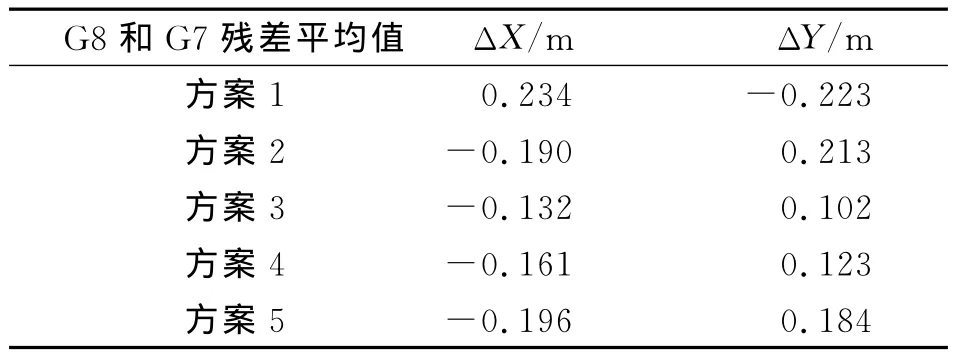
表4 公共点密度对坐标转换精度的影响情况Tab.4 Effect of common point density on the accuracy of coordinate transformation

3.3 七参数坐标转换模型的实现

在进行动态实验时，将七参数转换模型编写到车载导航系统中，通过实际比较，进行坐标转换的验证.为了验证平面转换模型在车载导航中应用的有效性，文中进行直线跑车实验，实验的原理是车载GPS通过沿规定的方向直线行走一段距离，在高斯投影过程中，分别选用方案1和方案2不同公共点分布进行测试，经过坐标转换程序，在VB界面上显示无人车行走的路径，根据平面转换生成连续的X、Y坐标数据来比较与实际路径的偏差值，并计算出最大值、最小值及均值，验证是否符合导航系统定位精度要求，实验环境选择大学校园操场内由北向南方向沿150m直线距离，图4～5中左图平面坐标系中的线段为车辆通过七参数模型转换得到的车道轨迹.

从图4～5可知，方案2的实测结果明显好于方案2的实测结果，且方案2偏差程度小于方案2的偏差程度，根据实测结果可知，使用方案2坐标转换精度满足车载GPS导航的定位精度.

为了进一步验证方案1的实用性和精确性，使用某一局部地形图作为实测区域，通过使用车载GPS接收机围校园局部区域进行数据采集，选择方案1中七参数转换模型进行坐标转换，把GPS接收下来的点转换成电子地图坐标系下的点，可见图6左边GPS采集实际的路径与转换后的的道路轨迹能够对应起来，满足车载导航定位精度的要求，实际的轨迹如图6所示.

鉴于Visual Basic设计界面简单的优点，实时性强，坐标转换方法编制成计算机程序可以嵌入到无人车的导航定位系统中，求出七参数后，用VB设计的坐标转换程序界面如图7所示.

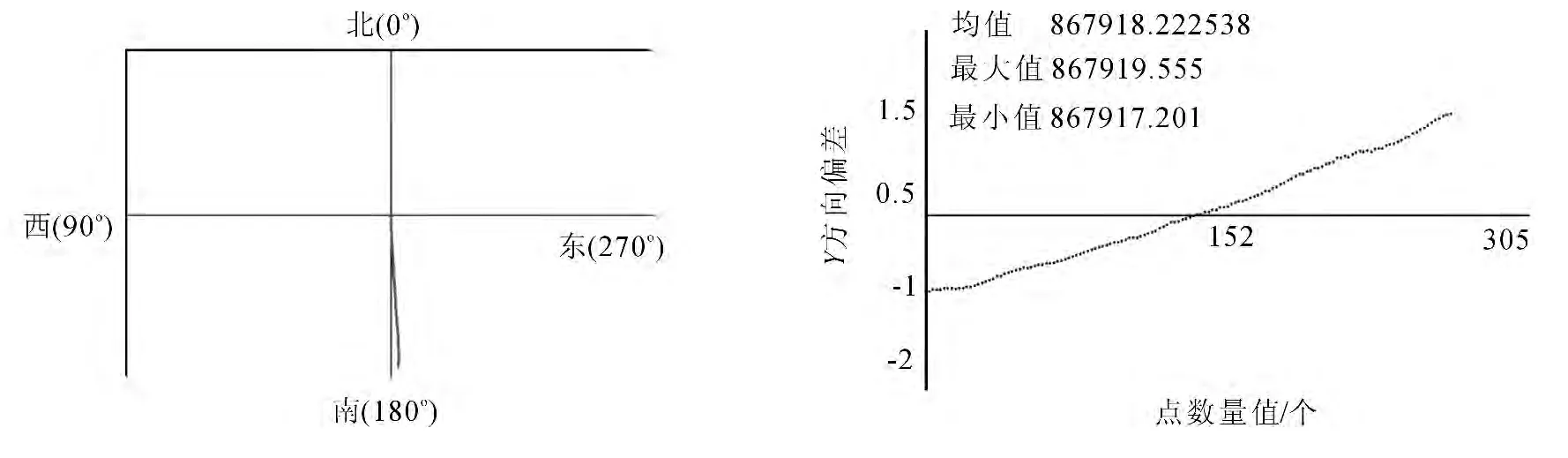
图4 方案1车载GPS接收机数据坐标转换结果显示Fig.4 Coordinate transformation from data received by GPS according to plan 1

图5 方案2车载GPS接收机数据坐标转换结果显示Fig.5 Coordinate transformation from data received by GPS according to plan 2

图6 车载GPS接收机数据坐标转换实测结果Fig.6 Measured results of coordinate transformation from data received by GPS

图7 坐标转换程序界面Fig.7 Coordinate conversion program interface

4 结论

文中在七参数转换模型基础上，在试验区域选用6个公共点，研究它们在整个测区的位置以及构成的地面网形，图形不同，面积不同，求解的转换参数也不同，为了改善坐标转换精度，最好选择位于测区外围、边长较长且能控制整个区域的网形.

当选择好固定的待测区域公共点的位置分布时，公共点的密度影响坐标转换的精度，当公共点的数量逐渐增加，其转换精度呈现先增加后减少的趋势.当相邻公共点距离在4～5km时，其转换精度提高了0.1～0.2m.

文中针对平面车载GPS导航定位精度进行研究，没有涉及高程，在实验区域内高程异常对坐标转换影响较小，对公共点的高程进行统一、简化转换算法，使其具有更高的实时性，适合车载嵌入式应用，满足车载GPS允许误差范围（＜0.5m）.

［1］杨帆，李广云，王力.三维坐标转换方法研究［J］.测绘通报，2010（6）：5.YANG Fan，LI Guang－yu，WANG Li.Research on the Methods of Calculating 3DCoordinate Transformation Parameters［J］.Bulletin of Surveying and Mapping，2010（6）：5.（in Chinese）

［2］王纯，张林让，陈广锋，等.用于GPS接收机的快速自适应干扰抑制方法［J］.西安电子科技大学学报，2011，38（3）：114.WANG Chun，ZHANG Lin－rang，CHEN Guangfeng，et al.Fast Adaptive Interference Suppression Method in the GPS Receiver［J］.Journal of Xidian University，2011，38（3）：114.（in Chinese）

［3］孔祥元，郭际明，刘宗泉.大地测量学基础［M］.武汉：武汉大学出版社，2001.KONG Xiang－yuan，GUO Ji－ming，LIU Zong－quan.Basis of Geodetic Measuring［M］.Wuhan：Wuhan University Press，2001.（in Chinese）

［4］段举举，沈云中.GPS／GLONASS组合静态相位相对定位算法［J］.测绘学报，2012，41（6）：825.DUAN Ju－ju，SHEN Yun－zhong.An Algorithm of Combined GPS／GLONASS Static Relative Positioning［J］.Acta Geodaeticaet Cartographica Sinica，2012，41（6）：825.（in Chinese）

［5］王文利，程传录，陈俊英.常用坐标转换模型及其实用性研究［J］.测绘信息与工程，2010，35（5）：37.WANG Wen－li，CHENG Chuan－lu，CHEN Jun－ying.Coordinate Transformation Model and Their Practicability［J］.Journal of Geomatics，2010，35（5）：37.（in Chinese）

［6］王广兴，何薇.二维空间与三维空间转换参数确定新法［J］.测绘通报，2009（5）：42.WANG Guang－xing，HE Wei.A New Method to Determine Parameter Conversion Between Two－dimensional and Three－dimensional Spaces［J］.Bulletin of Surveying and Mapping，2009（5）：42.（in Chinese）

［7］WANG J.An Approach to GLONASS Ambiguity Resolution［J］.Journal of Geodesy，2000，74：421.

［8］LEICK A.Aspects of GLONASS Carrier－phase Differencing［J］.GPS Solutions，1988，2（1）：36.

［9］MERA N S，ELLIOTT L，INGHAM D B.On the Use of Genetic Algorithms for Solving Ill－posed Problems［J］.Inverse Problems in Engineering，2003，11（2）：105.

［10］TITTERTON D H，WESTON J L.Strapdown Inertial Navigation Technology［M］.2nd ed.Lexington：MIT Lincoln Laboratory，2010.