基于ANSYS分析的高压输电塔结构动力特性研究

周 旸 苏桥磊

(1.中国电力工程顾问集团华北电力设计院工程有限公司，北京 100120； 2.北京沃利帕森工程技术有限公司，北京 100015)

基于ANSYS分析的高压输电塔结构动力特性研究

周 旸1苏桥磊2

(1.中国电力工程顾问集团华北电力设计院工程有限公司，北京 100120； 2.北京沃利帕森工程技术有限公司，北京 100015)

建立了某高压输电塔结构的梁—杆混合空间模型，应用ANSYS软件进行了该高压输电塔结构梁—杆混合空间模型的模态分析，利用子空间迭代法计算了该模型的前10阶自振周期、频率及振型，结果表明高压输电塔结构的梁—杆混合空间模型更接近于结构的实际受力状态，计算所得结构基本自振周期与现行建筑结构荷载规范经验公式及电力部门经验公式吻合较好。

高压输电塔，动力特性，模态分析，自振周期

0 引言

高压输电塔线体系属于典型的柔性结构，高度高，横截面小，质量轻，阻尼小，自振频率低，对风荷载十分敏感。近年来国内外有关学者对高压输电塔线体系的动力特性的计算模型和计算方法进行了研究，取得了一些进展[1-8]。然而由于导地线的非线性，使得高压输电塔线体系成为十分复杂的空间耦联体系，我国现行规范是将高压输电塔结构和导地线分别计算，不考虑导地线与高压输电塔结构之间的耦合作用[9]。本文不考虑导地线与高压输电塔结构之间的耦合作用，基于大型通用有限元分析程序ANSYS，应用模态分析理论，把某工程中实际使用的110 kV高压输电塔结构作为研究对象，建立有限元模型进行了模态分析。

1 高压输电塔的动力特性理论分析

1.1 结构模型选取

以前的工程计算出于简便考虑，通常将高压输电塔结构按空间桁架模型考虑，不考虑结构的剪力、弯矩引起的内力，但是利用这种方法建立的高压输电塔结构模型存在结构动力特性较差的问题。而要改善此类模型需要增加额外的附加杆件，由于额外的附加杆件的增加数量和位置带有一定的随机性，大大增加了模型的复杂程度。当然有限元分析高压输电塔结构也可以采用梁单元按空间刚架考虑，但因节点刚度较难确定，一般采用刚节点，这又人为地增大了高压输电塔结构的整体刚度。

而较为合理的模型处理方法应该是根据高压输电塔结构中不同杆件的实际工作状态来确定结构杆件的单元类型。塔身主材(弦杆)刚度较大，而且其在节点处实际上是连续的并不断开，可以按照梁单元来考虑。塔身斜材(主腹杆)两端与塔身主材连接，自身的刚度及端部约束也较大，也可以按照梁单元来考虑。辅助材(次腹杆)在结构的计算中仅仅起到减小塔身主材和塔身斜材计算长度的作用，并不需要计算其自身的内力，且其自身的刚度及端部约束都很小，还是可以按照杆单元来考虑的。

梁—杆混合空间模型是较为合理的高压输电塔结构的计算模型，该模型将主材、斜材和横隔材设置为梁单元可以承受轴力、弯矩、剪力，而辅助材设置为二力杆单元，仅仅承受轴力。这种处理方法使得主材、斜材的刚度偏大，而辅助材的刚度偏小，相互有所抵消，总的来说较为合理[10]。因此，本文采用梁—杆混合模型分析高压输电塔结构模态及相应的自振周期。

1.2 结构模态分析理论

无阻尼多自由度结构自振运动方程为：

(1)

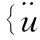
体系的频率方程为：

([K]-ω2[M]){φ}=0

(2)

式中：ω——固有频率；{φ}——振型特征向量。

求解式(2)即可获得体系的全部固有频率值。采用子空间迭代法就可以求出特征方程的全部阶特征值与特征向量，即可获得体系的全部自振频率和相应的振型。本文只需考虑求解结构前10阶自振频率和振型即可。

2 高压输电塔结构模型计算分析

2.1 有限元建模

本文选用某工程中实际使用的110 kV高压输电塔结构为原型。塔高38.2 m，呼高27 m，塔头宽度0.9 m，根开6.0 m，全角钢结构。塔身主材以及斜材、水平材、辅助材杆件分别使用Q345及Q235，弹性模量为2.1×106N/m2，泊松比为0.3，材料密度为7 800 kg/m3。采用ANSYS建模时，考虑到该高压输电塔结构为对称结构，以结构底面中心为坐标原点，垂直线路方向为x方向，顺线路方向为y方向，竖向为z方向，建立结构整体坐标系。将可以承受轴力、弯矩、剪力的主材、斜材和横隔材设置为梁单元，单元结构形式采用Beam189空间梁单元。仅仅承受轴力的辅助材设置为二力杆单元，单元结构形式采用Link8空间杆单元。该高压输电塔结构模型与基础间设置为刚性连接，全部约束其6个自由度，有限元模型见图1，共有120个节点，348个单元。

2.2 模态计算

应用有限元软件ANSYS对高压输电塔结构有限元模型进行模态分析，利用子空间迭代法，提取前10阶模态，可得该高压输电塔结构模型的前10阶自振频率、周期及其对应的振型。

表1为ANSYS有限元软件模态分析获得的前10阶自振频率和自振周期。

表1 高压输电塔结构的自振频率、周期及其对应的振型

3 结果分析

通常一般高耸结构的自振周期可由经验公式获得，现将高压输电塔结构有限元模型计算所得到的基本自振周期与现有规范计算所得的结构基本自振周期进行比较。

GB 50009-2012建筑结构荷载规范提供了一般高耸结构基本自振周期的经验公式：

T1=(0.007～0.013)H

(3)

其中，H为高压输电塔结构总高度。

其中混凝土可取计算的较小值，钢结构可取计算的较大值。该公式仅适用于具有连续变化外形和质量的一般高耸结构。而高压输电塔结构在高度方向一般都会有一个或者多个质量较大的横担，使得高压输电塔结构有时并不完全满足该经验公式的适用条件。

按该规范公式计算所得高压输电塔结构的自振周期取值范围为0.268～0.497。高压输电塔结构有限元模型计算所得结构基本自振周期为0.477，该值在规范公式计算范围之内。

而根据电力部门实测研究得到的计算高压输电塔结构基本自振周期的经验公式为：

(4)

式中：H——高压输电塔结构总高度；B——高压输电塔结构塔头宽度；b——高压输电塔结构腿部根开宽度。

根据式(4)计算所得该高压输电塔结构的基本自振周期为0.495，高压输电塔结构有限元模型计算所得结构基本自振周期0.477，两者相差3.64%，有限元模型计算所得结构基本自振周期与经验公式吻合较好。

4 结语

1)高压输电塔结构的梁—杆混合模型较空间桁架模型、钢架模型更能反映高压输电塔结构的实际受力状态，因此也更为合理。

2)高压输电塔结构有限元模型计算所得结构基本自振周期在建筑结构荷载规范经验公式计算范围之内，跟电力部门的经验公式计算结果相比也仅差3.64%，可以认为，本文所选取高压输电塔结构有限元模型和ANSYS分析方法，能较好的反映高压输电塔结构的实际振动状态。

3)高压输电塔结构形式多种多样、高度质量千差万别，细化针对不同结构类型、不同高度质量的高压输电塔结构的第一自振周期估算公式还需要再进一步的研究。

[1] Zou Lianghao，Liang Shuguo.Investigation of 3-D dynamic wind loads on lattice towers[J].Wind and Structures，2008，11(4):323-340.

[2] 梁枢果，邹良浩，赵 林，等.格构式塔架动力风荷载解析模型[J].同济大学学报(自然科学版)，2008，36(2):166-171.

[3] 梁枢果，朱继华，王力争.大跨越输电塔—线体系动力特性分析[J].地震工程与工程振动，2003，23(6):63-69.

[4] 邓洪洲，朱松晔，陈晓明，等.大跨越输电塔线体系气弹模型风洞试验[J].同济大学学报(自然科学版)，2003，31(2):132-137.

[5] 楼文娟，孙炳楠，叶 尹.高耸塔架横风向动力风效应[J].土木工程学报，1999，32(6):67-71.

[6] 梁枢果，邹良浩，韩银全，等.输电塔—线体系完全气弹模型风洞试验研究[J].土木工程学报，2010，43(5)：70-78.

[7] 梁 波，徐建良.架空输电铁塔动力风响应的数值模拟[J].同济大学学报(自然科学版)，2002，30(5):583-587.

[8] 刘 群，杨进春，周粼波.高压架空输电线路钢结构塔架与导线风致耦合振动现象研究[J].中国电力，1997，30(9):50-52.

[9] DL/T 5154-2002，架空送电线路杆塔结构设计技术规定[S].

[10] 周新华.高压输电铁塔结构强度分析[D].保定:华北电力大学，2002.

Research on dynamic features of high-voltage transmission tower structure based on ANSYS analysis

ZHOU Yang1SU Qiao-lei2

(1.NorthChinaPowerEngineeringCo.,LtdofChinaPowerEngineeringConsultingGroup,Beijing100120,China;2.BeijingWorleyParsonsEngineeringTechnicalCo.,Ltd,Beijing100015,China)

The paper establishes the beam-rod mixed space model of some high-voltage transmission tower structure, adopts ANSYS software to undertake the model analysis of the beam-rod mixed space model of the high-voltage transmission tower structure, applies the subspace iteration method to calculate the former 10 model self-vibration period, frequency and vibration type of the model, and proves by the result that the high-voltage transmission tower structure’s beam-rod mixed space model is close to the factual stressed status of the structure, and the calculated structural basic self-vibration period is consistent with the loading experience formula of current architectural structures and power departments.

high-voltage transmission tower, dynamic feature, model analysis, self-vibration period

1009-6825(2014)35-0052-02

2014-10-10

周 旸(1985- )，女，硕士，工程师； 苏桥磊(1980- )，男，硕士，工程师

TU311.3

A