输电塔减震控制中的GMM作动器优化布置研究
2014-08-11苏桥磊施菁华
周 旸 苏桥磊 施菁华 徐 成
(1.中国电力工程顾问集团华北电力设计院工程有限公司,北京 100120; 2.北京沃利帕森工程技术有限公司,北京 100015)
输电塔减震控制中的GMM作动器优化布置研究
周 旸1苏桥磊2施菁华1徐 成1
(1.中国电力工程顾问集团华北电力设计院工程有限公司,北京 100120; 2.北京沃利帕森工程技术有限公司,北京 100015)
对高压输电塔结构的动力特性和振动控制进行了研究,分析了GMM作动器在高压输电塔结构减震控制中的优化布置方法,并应用MATLAB软件中的遗传算法工具箱进行了优化布置结构、随机布置结构和无控结构的顶点位移计算,得到了一些对实际工程抗震设计具有参考意义的结论。
高压输电塔结构,GMM,遗传算法,优化布置
高压输电塔结构是一种常见的高耸结构,横向荷载起控制作用。传统的设计思想是用承重结构体系抵御横向荷载,存在着一定的局限性[1]。结构振动控制是一种不同于传统结构设计的全新的方法,它通过在结构上布置振动控制装置来改善结构的力学特性,使结构的承载力得以提高[2]。高压输电塔结构在地震作用下动力响应显著,采用减震控制来减小其动力响应是非常有效的方法[3-5]。
1 结构模型
本文以某110 kV角钢塔结构为原型,如图1所示。该角钢塔总高38.2 m,经过合理简化后共有120个节点,348根杆件,在部分杆件中集成了GMM作动器[6-9]进行整体结构的振动主动控制。

2 控制系统的控制原理
在高压输电塔结构中布置r个作动器后,在地震作用和控制力共同作用下结构体系的运动方程为:
(1)

(2)
其中,G1,G2,G3分别为位移、速度、加速度的增益矩阵。
将式(2)代入式(1),得:
(3)
对比式(1)和式(3)可以看出,施加主动控制力可以改变结构体系的阻尼、刚度和作用等动力特性。通过选择适当的控制算法和线性反馈函数,就可以控制高压输电塔结构的地震响应。
3 作动器的优化性能指标和优化算法
3.1 独立模态空间模型
对于实际的结构模型,只考虑控制系统前nc阶主模态,采用正则模态对式(3)进行解耦,令:
{X}=[φ]c{p}
(4)
(5)
{f}=[φc]T[D]{u}
(6)
3.2 优化准则
如果GMM作动器所布置的位置可以保证控制系统产生最大的模态控制力,那么这个位置就是最优的位置[10]。
令B=[φc]T[D],由式(6)可以得到:
{u}TA{u}=fTf
(7)
其中,A=BTB为正定对称矩阵。
可以证明下面不等式成立。
(8)
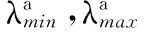
从式(8)可以看出,如果A的所有特征值均集中分布且很大时,就可以保证系统作动效率较高。因此可以定义一个作动器位置优化准则[11,12]。

(9)
3.3 优化步骤
高压输电塔遗传算法[11,13]流程如图2所示。

应用MATLAB软件编写程序,对性能指标进行调整得:
Fit=-(J0-J0×︳p-m∣)
(10)
其中,J0为调整前的适应度值;p为当前布置的作动器数目;m为预期布置的作动器数目。
数学模型为:
Find:[Bs]
min:Fit

4 优化计算
4.1 作动器布置数量对迭代规律的影响
在高压输电塔结构中分别布置不同数量的GMM作动器,应用遗传算法进行GMM作动器位置优化。图3~图5为布置60个,100个,140个作动器时适应度函数曲线。


从图3~图5可以看出随着遗传代数的增加,适应度函数值在不断减小,但是变化幅度越来越小,最后曲线趋于稳定,这说明适应度函数是收敛的;随着GMM作动器数量的增加,适应度函数曲线的收敛速度加快,这说明作动器的布置位置更优越。因此可知,利用遗传算法对高压输电塔结构进行作动器位置优化是可行的。
4.2 作动器布置数量对控制结果的影响
通过计算布置不同数量GMM作动器的高压输电塔结构顶点在无控和受控两种情况下的最大位移,比较不同数量的作动器对高压输电塔结构的控制效果。位移采用线性二次型经典最优控制算法(LQR)进行计算[14],以排除GMM作动器的输出性能对优化效果的影响。
图6~图8是布置不同数量GMM作动器和未布置GMM作动器时结构顶点X方向的位移时程对比图。
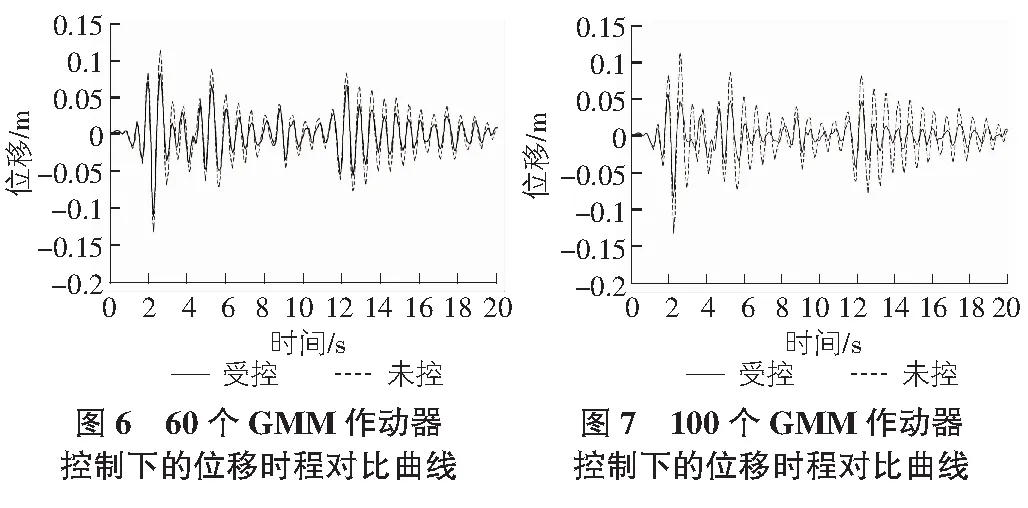
从图6~图8可以看出布置不同数量的GMM作动器对结构顶点位移均能起到明显的控制效果;GMM作动器数量越多,对顶点位移的控制越好;GMM作动器增加到一定数量后,再增加GMM作动器数量对控制效果的提高极为有限。综合考虑可行性与经济性,在该高压输电塔结构上布置100个GMM作动器是较为适宜的。

4.3 作动器布置位置对控制结果的影响
在该高压输电塔结构上布置100个GMM作动器,通过优化布置、随机布置和不布置三种情况下的结构顶点X方向位移进行对比。由图9可以看到GMM作动器经优化布置后的控制效果明显优于随机布置的控制效果,可提高20%左右。这说明利用遗传算法对GMM作动器的布置位置进行优化是有效的。
5 结语
1)适应度函数值随着遗传代数的增加,逐渐收敛最终趋于稳定;优化性能指标计算值随着GMM作动器数量的增加而增大,GMM作动器的布置位置更加合理。利用遗传算法对高压输电塔结构进行作动器位置优化是可行的。
2)在高压输电塔结构中布置GMM作动器能够减小结构位移,在高压输电塔结构上布置100个GMM主动控制系统较为适宜,对结构位移的控制效果能达到35%左右。
3)GMM主动控制系统优化布置控制效果要好于随机布置,可提高20%左右。利用遗传算法对GMM作动器的布置位置进行优化是有效的。
[1] 李宏男.高压输电塔抗震分析与设计[M].北京:中国电力出版社,2009:28.
[2] 周福霖.工程结构减震控制[M].北京:地震出版社,1997.
[3] 欧进萍.结构振动控制——主动、半主动和智能控制[M].北京:科学出版社,1993:1-10.
[4] Yao J T P.Concept of structural control[J].Strctural Division,ASCE,1972,98(7):39-40.
[5] 王肇民,马人乐.塔式结构[M].北京:科学出版社,2004:313.
[6] 邓 睿.超磁致伸缩执行器微位移控制系统的研究[D].大连:大连理工大学,2006.
[7] 唐志峰.超磁致伸缩执行器的基础理论与实验研究[D].杭州:浙江大学,2005.
[8] 王晓煜.超磁致伸缩微位移执行器的系统建模与控制方法研究[D].大连:大连理工大学,2007.
[9] 孙 乐.超磁致伸缩材料的本构理论研究[D].兰州:兰州大学,2007.
[10] 容 里.压电作动器设计及双层球面网壳结构振动主动控制研究[D].杭州:浙江大学,2008.
[11] 曾 光,李东旭.空间智能桁架作动器/传感器位置优化中的遗传算法应用[J].宇航学报,2007,28(2):461-464.
[12] 孙东昌,张洪华.压电智能梁振动控制中致动片优化布置与实验[J].中国空间科学技术,1999,12(6):46-52.
[13] 唐文艳,顾元宪.遗传算法在结构优化中的研究进展[J].力学发展,2002,32(1):26-27.
[14] 张 目.压电智能桁架的最优控制及优化设计[D].大连:大连理工大学,2009.
Research of optimal allocation of GMM actuator in seismic control of power transmission tower
ZHOU Yang1SU Qiao-lei2SHI Jing-hua1XU Cheng1
(1.NorthChinaPowerEngineeringCo.,Ltd,ofChinaPowerEngineeringConsultingGroup,Beijing100120,China;2.BeijingWorleyparsonsEngineeringandTechnicalCo.,Ltd,Beijing100015,China)
The paper researches the dynamic features and vibration control of the high-voltage power transmission tower structure, analyzes the optimal allocation of GMM actuator in seismic control of power transmission tower, undertakes the optimal allocation structure and random allocation structure, and vertex displacement calculation of non-controlled structures, by adopting the genetic algorithm toolbox in MATLAB software, and concludes the reference for the engineering anti-seismic design in factual projects.
high-voltage power transmission tower structure, GMM, genetic algorithm, optimal allocation
1009-6825(2014)28-0034-03
2014-07-23
周 旸(1985- ),女,硕士,工程师; 苏桥磊(1980- ),男,工程师; 施菁华(1974- ),女,高级工程师; 徐 成(1984- ),男,工程师
TU323
A
