正常组织并发症概率模型综述

朱 健 李宝生 舒华忠 白 曈 尹 勇 罗立民DE CREVOISIER Renaud

1(山东省肿瘤防治研究院， 济南 250117)2(山东省放射肿瘤学重点实验室， 济南 250117)3 (东南大学影像科学与技术实验室， 南京 210096)4(雷恩第一大学信号与图像实验室(INSERM-U1099)， 雷恩 35510，法国)

正常组织并发症概率模型综述

朱 健1,2李宝生1,2舒华忠3*白 曈1,2尹 勇1,2罗立民3DE CREVOISIER Renaud4

1(山东省肿瘤防治研究院， 济南 250117)2(山东省放射肿瘤学重点实验室， 济南 250117)3(东南大学影像科学与技术实验室， 南京 210096)4(雷恩第一大学信号与图像实验室(INSERM-U1099)， 雷恩 35510，法国)

通过分析肿瘤放疗及并发症随访数据，拟合正常组织并发症概率(NTCP)模型参数，并由此预测并发症发病率、优化放疗方案、揭示正常组织放射生物学特性，是肿瘤放射生物物理学近期的研究热点。综述相关文献中提出的6种NTCP模型，并讨论建模及对比模型预测能力的方法；然后介绍近年来提出的几种改进后的NTCP模型，以及几种新的并发症预测技术。从开展临床应用的角度，对NTCP模型的研究现状、存在的问题和发展趋势做概括和总结，就NTCP模型在个体化放疗中的应用等问题进行讨论和展望。

肿瘤；放射治疗；并发症；预测模型

引言

肿瘤放射治疗引起正常器官的损伤，不仅限制了处方剂量的提升，而且也直接影响了患者的生存质量和生存率[1-2]。正常组织并发症概率(normal tissue complication probability, NTCP)是建立在剂量-体积关系上的一种数学模型，可以通过调整模型参数，描述不同正常器官在接受一定照射剂量后出现放疗并发症的概率，从而对放疗毒性反应进行预测[3-5]，也可据此对不同的治疗方案进行生物效应的量化对比[6-8]。大量的研究工作借助NTCP，对放疗临床及放射物理学数据进行分析，以优化放疗方案，了解正常器官的生物学特性[9-14]。文中首先总结文献报道的6种NTCP模型，并介绍建立具有群体针对性的NTCP模型及对比不同NTCP模型预测能力的方法；然后介绍近年来针对不同剂量分割方案、不同随访时间、个体化放疗提出的几种改进后的NTCP模型，以及几种新的并发症预测技术。

1 NTCP模型

1.1Lyman-Kutcher-Burman(LKB)模型

LKB模型是应用最为广泛的NTCP模型。Lyman[15]首先提出了S形剂量效应(sigmoid dose response, SDR)积分模型，用来描述正常组织全部或部分体积受到均匀剂量D照射后的剂量效应，表示为

(1)

(2)

式中，TD50(1)为全部体积受照射时引起某种器官出现50%并发症概率所需的剂量，m为剂量响应曲线斜率因子。

随着放疗特别是适形和调强技术的发展、正常组织受量不均匀程度增加，Kutcher、Burman[16-17]和Lyman[18]相继提出了两种剂量-体积直方图(DVH)化简算法，对原有SDR模型进行了改进，即等效体积法(effective volume reduction scheme，见式(3)～式(6))和等效剂量法(effective dose reduction scheme，见式(7)～式(8)，有

(3)

(4)

(5)

(6)

(7)

(8)

式中：n为体积效应因子，体积效应与n成正比，n值越大(接近于1)体积效应越大，n值越小(接近于0)体积效应越小。

vij和Dij是将患者i的积分DVH转化为微分形式后对应的第j个体积单元和该体积单元接受的照射剂量，vij之和等于100；dij则是对每个剂量单元进行了归一化，dij之和等于1。大体积效应意味着NTCP更多地依赖于整个体积内受照时的平均剂量，对应于“并型”组织和器官，如肺、肝、肾；小体积效应意味着NTCP应该用受照体积内最大剂量计算，对应于“串型”组织和器官，如脊髓、食道、直肠。太少的剂量-体积分割单元(如10 Gy/单元)不足以准确描述器官的剂量-体积信息，而过细的分割(如1 cGy/单元)增加了计算量且并不会对参数拟合和NTCP计算结果产生影响。Dawson[9]推荐j介于50～150之间。式(1)～式(8)表述LKB是一个F(TD50(1),n,m; (Dij，vij))结构的三参数加剂量-体积信息的概率模型。Moiseenko[19]对比了等效体积和等效剂量两种DVH化简方法，认为相比于等效体积方法，等效剂量法对于器官内的剂量分布变化更不敏感。

1.2Logit-EUD模型和Schultheiss模型[20]

Schultheiss首先提出了描述均匀照射下剂量D与NTCP关系的逻辑模型，有

(9)

式中，TD50(1)和k是模型参数，前者意义与LKB模型中的TD50(1)相同，后者为斜率因子。

考虑到非均匀照射下的计算，用式(8)描述的等效均匀剂量(effective uniform dose，EUD)替换均匀剂量D，以此引入体积效应因子n和患者i的DVH信息，这样就形成了Logit-EUD模型，可用于非均匀照射下正常组织并发症概率的计算。

Schultheiss模型是一个直接针对非均匀照射的积分概率模型，有

(10)

假设患者“i”的某正常器官由N个足够小的子单元构成，每个子单元接受到的照射剂量可视为均匀剂量，第一步按式(9)计算子单元“j”的NTCP值，代入(10)计算整个器官的NTCP值。Schultheiss模型仅有两个参数：TD50(1)和k。

1.3Poisson-EUD模型和Källman模型[21]

Källman提出了描述均匀剂量照射下剂量D和NTCP关系的泊松概率模型，有

(11)

式中，TD50(1)和γ是模型参数，与Logit-EUD模型相似。

考虑到非均匀照射下的计算，用式(8)描述的EUD替换均匀剂量D，以此引入体积效应因子n和患者i的DVH信息，这样就形成了Poisson-EUD模型，可用于非均匀照射下正常组织并发症概率的计算。

与Schultheiss模型相同，Källman模型同样是直接针对非均匀照射情况。假设患者i的某正常器官由N个足够小的子单元构成，每个子单元接受到的照射剂量可视为均匀剂量，先按式(11)计算子单元j的NTCP值，再代入式(12)计算整个器官的NTCP值。Källman模型有3个参数：TD50(1)、γ和s。

(12)

1.4Parallel模型

Parallel模型综合了Wolbarst、Niemierko和Jackson提出的理论[22-24]，假设正常器官是由并型结构的独立功能单元(independent functional subunits，FSU)构成，仅当大量FSU被破坏且超过功能储备分布(functional reserve distribution)描述的阈值时，器官才表现出并发症。对于典型的串型器官，以该模型的理论将其假设为仅有一个FSU组成，只要该FSU受到破坏，整个器官就可能表现出并发症。Jackson指出，当FSU数量较大时，整个器官的损伤更近似于FSU的平均损伤[25]。因此，猜测Parallel模型对于描述典型的串型器官可能存在一定误差或者局限性；而前期试验结果也表明，在对直肠并发症进行参数拟合时，仅有Parallel模型无法得到有效的拟合结果。对于患者i，有

(13)

(14)

(15)

Parallel模型包括4个参数：d1/2表示导致50%FSU被破坏的照射剂量；k为斜率因子，体现了FSU在d1/2剂量照射下出现损伤的增长率；V50和σv分别描述功能储备的平均值及宽度。

2 建立具有群体针对性的NTCP模型

Burman应用Lyman提出的并发症概率模型[15]，在Emami给出的各器官临床耐受剂量[1]的基础上，通过曲线拟合和观察的方法，给出了27种正常器官在接受全体积均匀照射的情况下出现29种放疗并发症的NTCP模型参数(TD50(1)，n，m)[26]。这一结果沿用至今，被Pinnacle等商业计划系统的生物学评估模块所引用[27]。然而，随着精确放疗技术的发展，多数正常器官受到的是部分体积的非均匀照射，继续沿用Burman给出的参数来预测放疗并发症，或者以此对放疗方案做出量化评估，其准确性势必将受到影响。这就要求在临床观察和数据分析的基础上，建立具有群体针对性的NTCP模型，即拟合新的模型参数，以充分发挥NTCP模型在预测并发症和量化评估放疗计划方面的作用。

各模型参数的拟合均采用最大似然估计法(maximum likelihood method)。对于患者i，无论用哪种模型，其NTCP值均可表述为模型参数和微分后剂量-体积单元函数的形式，即

NTCPi=F(parameters,di,vi)

(16)

则对于用来拟合模型参数的一组患者数据，其对数似然函数(log-likelihood equation)L可表示为

L(Parameters;di,vi)=

(17)

式中，对于患者i，如果临床观察出现放疗并发症，则Ri=1，否则Ri=0。

利用优化工具，使似然函数L取最大值，即拟合得到各模型参数。优化过程可利用Matlab软件(The MathWorks, Inc.)中提供的遗传算法(genetic algorithm)、单纯形算法(simplex)和约束非线性优化算法(constrained nonlinear optimization)等诸多既有库函数实现。

图1 验证LKB模型参数拟合结果的log-likelihood profile projection图[10]。(a)参数TD50；(b)参数n；(c)参数mFig.1 Log-likelihood profile projection plots to check the fitting results of LKB model[10]. (a) Parameter TD50; (b) Parameter n; (c) Parameter m

对于拟合得到的一组NTCP模型参数，是否达到了全局最优点，可以通过勾画log-likelihood profile projection图的形式进行验证。如图1所示，以LKB模型为例，令n和m取拟合得到的参数值不变，TD50(1)在可能的取值区间内变化，观察似然函数值L是否在拟合得到的TD50(1)处取得最大值，以此验证参数TD50(1)“最大似然估计”拟合的有效性，另外两个参数同理。通过勾画profile图，还可以获得该参数与某似然函数值所对应的置信区间。利用拟合得到的一组模型参数，可以计算该患者群体中每一例患者的NTCP值；将该组患者NTCP值的平均数与观察得到的并发症发病率进行比对，两个数值越接近说明拟合效果越好、预测结果越准确。另外，如图2所示，也可以通过勾画点散图的形式，将患者按计算得到的NTCP值排序，并均匀地分为若干组，找出每组患者NTCP均值和观察得到的该组患者并发症发病率的对应关系。各组数据越紧密地分布在45°对角线两侧，即计算得到的NTCP值(calculated NTCP)与观察得到的并发症概率(observed NTCP)结果越相近，则说明预测效果越好，也就是说，该模型和该组参数可用于对后续接受放疗的患者在实施治疗前预测其出现并发症的概率。

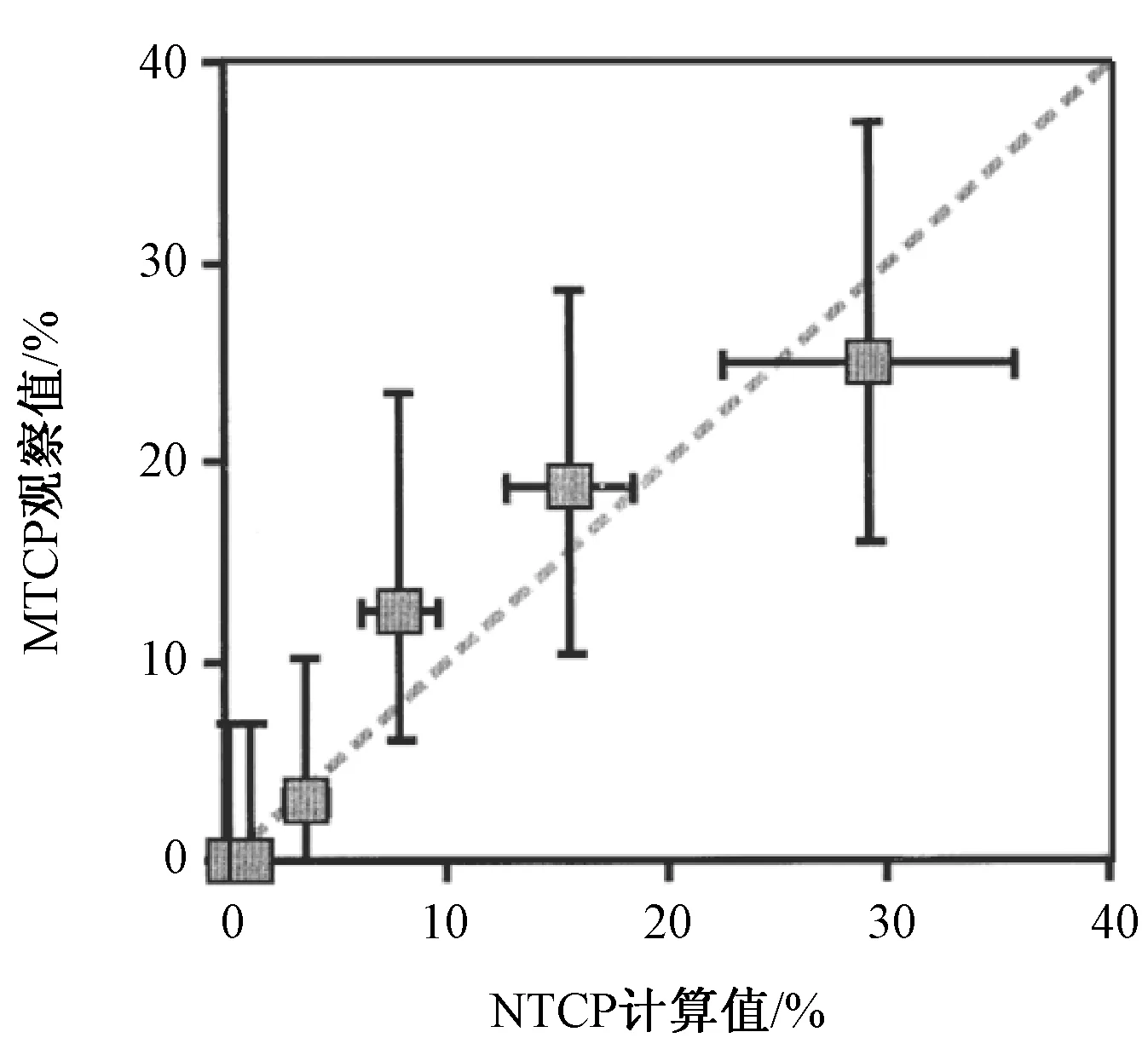
图2 定性地验证预测得到的NTCP值和观察得到的并发症发生概率间的相关性[9]Fig.2 Qualitatively relationship between observed toxicity rate and calculated NTCP values[9]

3 NTCP模型预测能力对比

通过勾画ROC(receiver operating characteristic)图和计算Efron’s pseudo R2值的形式，可以对比各模型在预测同一并发症时表现出的能力。图3展示了对比Random Forest方法与6种NTCP模型预测直肠晚期并发症(LENT/SOMA标准≥Grade2)的情况：曲线越接近坐标空间左上角，表明预测能力越好；越接近对角线，表明预测效果越接近于“抛硬币”。图例中括号内的值是各曲线下方围成的面积，可以看到，6种NTCP模型在预测膀胱晚期并发症时，表现出了几乎相同的预测能力。

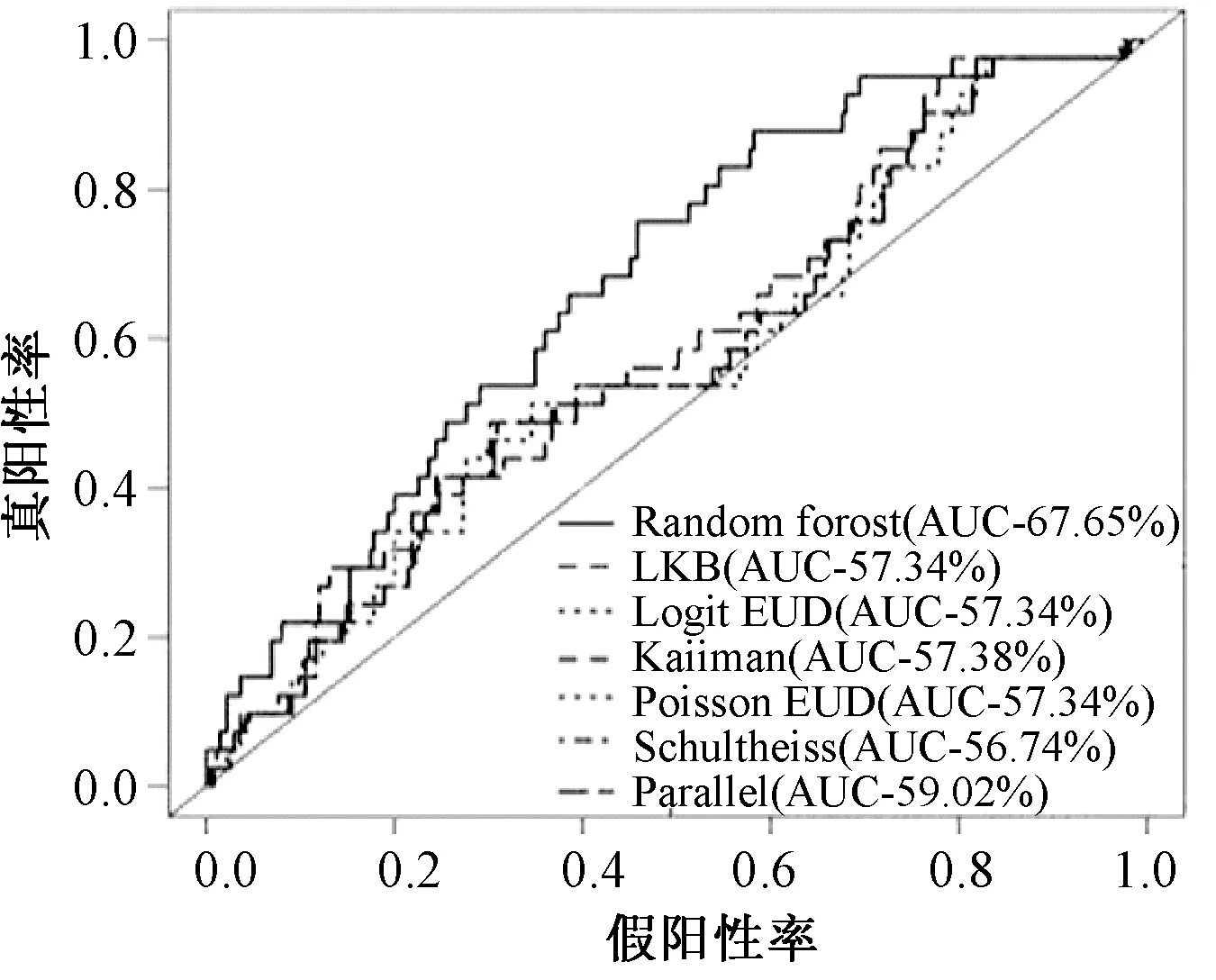
图3 Ospina等[28]对比NTCP模型预测能力的ROC图Fig.3 ROC plot to compare the predictive capability of NTCP models from Ospina et al.[28]

Rancati等对比了LKB(LEUD)、Logit-EUD(LOGEUD)、Poisson-EUD(PEUD)和Källman(RS)4种模型在预测前列腺癌引起的直肠晚期损伤(出血)时表现出的差异，认为4种模型具有相似的能力，因此可以在实际应用时选择采用数学形式更为简单的Logit-EUD模型[29]；Seppenwoolde等对比了Parallel、LKB、Källman(Seriality)3种NTCP模型以及MLD(平均肺受量)、VDth在预测放射性肺炎时表现出的能力，认为各模型绘制的曲线相似，即使是最简单的预测指标MLD，也表现出与复杂的NTCP模型相近的预测水平[30]；Moiseenko等对比了Lyman、Källman和Schultheiss 3种NTCP模型在预测人体放射性肝损伤和动物放射性脊髓损伤时表现出的差异，认为不同的NTCP模型由于使用了不同的DVH化简方法或者不同的模型参数，会计算得到截然不同的NTCP值[19]。

4 对NTCP模型的改进

NTCP模型表现出了良好的预测能力，也为放疗医生和物理师对比不同治疗方案提供了一个量化的评价标准。然而，在用单纯数学手段解决复杂的生物学问题时，常会因其局限性而出现偏差，且上述传统的NTCP模型多在上世纪八九十年代提出，导致其在现阶段的使用也存在着一定的局限性，特别是在个体化放疗领域，传统的NTCP模型仅能面向单一患者群体描述器官受量与并发症的关系，无法体现“量体裁衣”的个体化放疗思想：一方面，NTCP值的计算完全基于器官受到的最终剂量-体积信息，无法区分这些剂量是如何累加得到的，也就没法区别预测常规分割和非常规分割组的并发症概率，而临床经验表明，不同剂量的分割方案将显著影响正常器官的损伤概率；另一方面，在拟合NTCP模型参数或预测放疗并发症时，其结果与并发症的表现时间密切相关，同一患者的并发症表现情况及严重程度会因随访时间的不同而出现变化，这就直接影响了参数拟合过程中似然函数的表达；再一方面，上述传统NTCP仅描述正常组织接受辐射的剂量-体积与并发症概率的关系，未能考虑其他个体因素对并发症表现产生的影响。

面对上述三方面局限，有学者对传统NTCP模型做出了改进：

针对分次剂量不同的情况，可以将NTCP模型与线性-二次(L-Q)模型[31, 32]相结合，引入α/β因子作为另一个模型参数，对剂量单元Di进行校正。以预测直肠损伤的NTCP模型为例，Marzi和Tucker均应用该方法对NTCP模型进行了改进，同时拟合了描述直肠生物学特性的α/β值[33,34]。将该α/β值代入改进后的NTCP模型，就可以将放疗计划中投放的物理剂量转换成患者吸收的生物剂量，消除了不同分次剂量治疗带来的生物学差异，提高了NTCP模型对并发症预测的精度。

针对随访时间对NTCP模型的影响，Tucker提出了一种混合的NTCP模型[35]，在现有模型的基础上，引入新的模型参数μ和σ，构成“对数正态分布”函数对潜在时间建模。由此，患者i在时间τ表现并发症对似然函数的贡献变为NTCP与时间概率密度函数f(τ)的乘积，若在时间τ内未表现并发症，则贡献为1-NTCP·f(τ)。该方法改变了传统NTCP模型必须指定某一并发症观察点的局限，允许将并发症表现时间不同的患者纳入同一组进行分析，使NTCP模型在描述并发症与辐射剂量关系的同时，引入表达时间因素，拓展了NTCP模型的功能和包含的信息量。

传统意义上的NTCP模型只能描述正常器官受到照射的剂量-体积因子与并发症概率间的关系，而大量研究数据及临床经验证实，并发症的出现与其他因素有着显著相关性，比如患者自身因素(是否有吸烟史、糖尿病史、手术史等)、化疗方案因素、病理分期因素等。这些因素的出现与否，在一定程度上显著影响着每一个患者个体是否出现放疗并发症的结果，使具有相同DVH曲线的患者可能表现出截然不同的并发症情况。Tucker等提出了一种广义的Lyman NTCP模型[35]，该模型在传统模型3个参数的基础上，增加了剂量修正因子(dose-modifying factor，DMF)，将“有否吸烟史”这一非剂量学因素引入NTCP模型，并通过分析一组非小细胞肺癌患者出现放射性肺炎的随访数据，拟合得到“有否吸烟史”对应的DMF因子。利用这一技术，就可以有针对性地根据患者的个体情况进行个体化的并发症概率预测，扩展了NTCP模型的应用领域。

上述3种针对NTCP模型的改进，均着眼于目前先进的放疗技术对并发症表达带来的影响，通过增加模型参数、改变模型表达形式的方法，提高了NTCP模型预测放疗并发症的能力，是目前放疗领域的研究热点，具有广阔的应用前景。

5 其他几种放疗并发症预测方法

Munley和Su先后利用人工神经网络，对临床治疗数据进行了分类，使该神经网络经过训练后，可以针对相同的临床数据源预测放射性肺损伤[36,37]。Thames等提出了一种用于并发症预测的集群模型(Cluster model)[38]，提出并发症的表现不仅与正常器官受到的辐射剂量有关，而且与构成正常器官的功能子单元空间分布(集群)情况有关，并将器官按空间结构分为一维(如脊髓)、二维(如直肠壁)和三维(如肺)。El Naqa等提出利用交叉验证(Cross-Validation)技术[39]，在众多临床预后因素构成的海量数据中进行数据挖掘和建模，进而利用最密切相关的因素进行并发症预测，这体现了多因素引导下的并发症预测的思想。Valdagni等在分析临床数据的基础上，建立了预测前列腺癌放疗并发症的诺莫图(Nomo-gram)[40]，对可能引起并发症的多种因素进行加权，是一种降低预测精度但简化使用过程的简便易行的方法。Deasy和Acosta均将并发症与解剖结构关联起来，分别从胸部正交投影图像(anterior-posterior projection image)和盆腔CT三维重建图像空间，标注了放射性肺炎和放射性直肠损伤的高危区域[41,42]。Ospina等对比了随机森林(random forest)方法与传统的NTCP模型在预测前列腺癌引起直肠晚期损伤中表现出的特点，结果显示这种基于二叉树理论的分类方法成功地将多种临床因素引入到并发症筛选过程中，与人工神经网络方法类似，可以有效地针对相同的临床数据源，预测并发症概率[28]。

上述几种方法，充分利用先进的计算机信息处理技术，对临床数据和随访结果进行分析、分类，是将计算机技术应用于临床医学的成功案例，在肿瘤放疗并发症预测这一领域，为两个学科提供了一个交叉合作平台。

6 NTCP模型应用过程中的注意事项

对NTCP模型参数的拟合，需要建立在一组临床观察结果的基础上，其入组患者数量(样本大小)决定着是否可以成功拟合出合理的模型参数。基于前期实验及研究经验，发现当样本数量大于120例时，似然函数值趋于稳定，模型趋于收敛。然而，这一数值并不能作为一个固定的标准，若入组患者的“均匀性”差异较大，比如患者接受的治疗方案(包括化疗、放疗计划及分次剂量)有较大的差异，则样本数量需要继续增加；反之，更少的样本数量也可以达到预期的效果。

对于同一患者出现的放疗并发症，若使用的评级标准不同，其分级结果也将受到影响，即似然函数(公式17)中的Ri取值将有所不同。使用RTOG、LENT/SOMA和CTCAE不同标准的相关工作均有报道，因此在对NTCP模型进行参数拟合时，使用何种并发症评级标准也应予以说明。

7 展望

NTCP模型通过简单的数学形式，描述了器官受辐射剂量-体积因子与该器官出现并发症概率之间的关系。经过多年研究，该模型出现了不同表现形式，在定量评估放疗计划方面表现出了积极的意义，也对不同正常组织的放射生物学特性做出了有针对性的描述。

随着放疗技术的进一步发展，特别是调强放疗技术的广泛应用，一种基于生物准则的调强放疗计划设计理念及其相应的生物放疗计划系统[43]也已经逐渐成为研究热点和应用主流，而NTCP模型正是完成调强放疗生物优化的主要因素，其参数及约束项的合理设置，特别是结合具有个体针对性的改进的NTCP模型，将提高调强放疗计划在保护肿瘤周围危及器官方面的性能。因此，对NTCP模型的研究仍具有广阔的前景。

致谢(感谢法国雷恩第一大学(Université de Rennes 1)信号与图像实验室(Laboratoire Traitement du Signal et de l’Image, INSERM-U1099)的Juan David OSPINA、Antoine SIMON和Pascal HAIGRON在NTCP模型参数拟合和统计分析工作中给予的帮助)。

[1] Emami B, Lyman J, Brown A,etal. Tolerance of normal tissue to therapeutic irradiation [J]. Int J Radiat Oncol Biol Phys, 1991,21: 109-122.

[2] Marks LB, Yorke ED, Jackson A,etal. Use of normal tissue complication probability models in the clinic [J]. Int J Radiat Oncol Biol Phys, 2010,76: S10-19.

[3] Tucker SL, Li M, Xu T,etal. Incorporating single-nucleotide polymorphisms into the Lyman model to improve prediction of radiation pneumonitis [J]. Int J Radiat Oncol Biol Phys, 2013,85: 251-257.

[4] Strigari L, Pedicini P, D’Andrea M,etal. A new model for predicting acute mucosal toxicity in head-and-neck cancer patients undergoing radiotherapy with altered schedules [J]. Int J Radiat Oncol Biol Phys, 2012,83: e697-e702.

[5] Gulliford SL, Partridge M, Sydes MR,etal. Parameters for the Lyman Kutcher Burman (LKB) model of Normal Tissue Complication Probability (NTCP) for specific rectal complications observed in clinical practise [J]. Radiother Oncol, 2012,102: 347-351.

[6] Fellin F, Azzeroni R, Maggio A,etal. Helical tomotherapy and intensity modulated proton therapy in the treatment of dominant intraprostatic lesion: A treament planning comparison [J]. Radiother Oncol, 2013,107(2):207-212.

[7] Amin NP, Miften M, Thornton D,etal. Effect of induction chemotherapy on estimated risk of radiation pneumonitis in bulky non-small cell lung cancer [J]. Med Dosim, 2013,38: 320-326.

[8] De Sanctis V, Bolzan C, D’Arienzo M,etal. Intensity modulated radiotherapy in early stage Hodgkin lymphoma patients: is it better than three dimensional conformal radiotherapy? [J]. Radiat Oncol, 2012,7: 129.

[9] Dawson LA, Normolle D, Balter JM,etal. Analysis of radiation-induced liver disease using the Lyman NTCP model [J]. Int J Radiat Oncol Biol Phys, 2002,53: 810-821.

[10] Chapet O, Kong FM, Lee JS,etal. Normal tissue complication probability modeling for acute esophagitis in patients treated with conformal radiation therapy for non-small cell lung cancer [J]. Radiother Oncol, 2005,77: 176-181.

[11] Fiorino C, Rancati T, Valdagni R. Predictive models of toxicity in external radiotherapy: dosimetric issues [J]. Cancer, 2009,115: 3135-3140.

[12] Miah AB, Gulliford SL, Clark CH,etal. Dose-response analysis of parotid gland function: What is the best measure of xerostomia? [J]. Radiother Oncol, 2013,106: 341-345.

[13] 徐志勇, 梁世雄, 朱冀, 等. 用Lyman NTCP模型分析原发性肝癌三维适形放疗引起的放射性肝病 [J]. 中华放射肿瘤学杂志, 2006,15: 457-461.

[14] Zhu Jian, Zhang Zicheng, Li Baosheng,etal. Analysis of acute radiation-induced esophagitis in non-small-cell lung cancer patients using the Lyman NTCP model [J]. Radiother Oncol, 2010,97: 449-454.

[15] Lyman JT. Complication probability as assessed from dose-volume histograms [J]. Radiat Res Suppl, 1985,8: S13-S19.

[16] Kutcher GJ, Burman C, Brewster L. Histogram reduction method for calculating complication probabilities for three-dimensional treatment planning evaluations [J]. Int J Radiat Oncol Biol Phys, 1991,21: 137-146.

[17] Kutcher GJ, Burman C. Calculation of complication probability factors for non-uniform normal tissue irradiation: the effective volume method [J]. Int J Radiat Oncol Biol Phys, 1989,16: 1623-1630.

[18] Lyman JT, Wolbarst AB. Optimization of radiation therapy, IV: A dose-volume histogram reduction algorithm [J]. Int J Radiat Oncol Biol Phys, 1989,17: 433-436.

[19] Moiseenko V, Battista J, Van Dyk J. Normal tissue complication probabilities: dependence on choice of biological model and dose-volume histogram reduction scheme [J]. Int J Radiat Oncol Biol Phys, 2000,46: 983-993.

[20] Schultheiss TE, Orton CG, Peck RA. Models in radiotherapy: volume effects [J]. Med Phys, 1983,10: 410-415.

[21] Kallman P, Agren A, Brahme A. Tumour and normal tissue responses to fractionated non-uniform dose delivery [J]. Int J Radiat Biol, 1992,62: 249-262.

[22] Wolbarst AB, Chin LM, Svensson GK. Optimization of radiation therapy: integral-response of a model biological system [J]. Int J Radiat Oncol Biol Phys, 1982,8: 1761-1769.

[23] Niemierko A, Goitein M. Modeling of normal tissue response to radiation: the critical volume model [J]. Int J Radiat Oncol Biol Phys, 1993,25: 135-145.

[24] Jackson A, Kutcher GJ, Yorke ED. Probability of radiation-induced complications for normal tissues with parallel architecture subject to non-uniform irradiation [J]. Med Phys, 1993,20: 613-625.

[25] Jackson A, Ten Haken RK, Robertson JM,etal. Analysis of clinical complication data for radiation hepatitis using a parallel architecture model [J]. Int J Radiat Oncol Biol Phys, 1995,31: 883-891.

[26] Burman C, Kutcher GJ, Emami B,etal. Fitting of normal tissue tolerance data to an analytic function [J]. Int J Radiat Oncol Biol Phys, 1991,21: 123-135.

[27] Härdemark B, Liander A, Rehbinder H,etal. P3IMRT Biological optimization and EUD [EB/OL]. Pinnacle3 White Paper. www. edu-doc.com/ebook/hardemark.html,2004/2013-05-11.

[28] Ospina J, Zhu Jian, Le Prise E,etal. Random forest are strong competitors of published NTCP models for rectal and bladder toxicity prediction[J]. Int J Radiat Oncol Biol Phys, 2012,84: S387.

[29] Rancati T, Fiorino C, Gagliardi G,etal. Fitting late rectal bleeding data using different NTCP models: results from an Italian multi-centric study (AIROPROS0101) [J]. Radiother Oncol, 2004,73: 21-32.

[30] Seppenwoolde Y, Lebesque JV, de Jaeger K,etal. Comparing different NTCP models that predict the incidence of radiation pneumonitis. Normal tissue complication probability [J]. Int J Radiat Oncol Biol Phys, 2003,55: 724-735.

[31] Douglas BG, Fowler JF. The effect of multiple small doses of x rays on skin reactions in the mouse and a basic interpretation [J]. Radiat Res, 1976,66: 401-426.

[32] Thames HD, Jr Withers HR, Peters LJ,etal. Changes in early and late radiation responses with altered dose fractionation: implications for dose-survival relationships [J]. Int J Radiat Oncol Biol Phys, 1982,8: 219-226.

[33] Marzi S, Saracino B, Petrongari MG,etal. Modeling of alpha/beta for late rectal toxicity from a randomized phase II study: conventional versus hypofractionated scheme for localized prostate cancer [J]. J Exp Clin Cancer Res, 2009,28: 117.

[34] Tucker SL, Thames HD, Michalski JM,etal. Estimation of alpha/beta for late rectal toxicity based on RTOG 94-06 [J]. Int J Radiat Oncol Biol Phys, 2011,81: 600-605.

[35] Tucker SL, Liu HH, Liao Z,etal. Analysis of radiation pneumonitis risk using a generalized Lyman model [J]. Int J Radiat Oncol Biol Phys, 2008,72: 568-574.

[36] Munley MT, Lo JY, Sibley GS,etal. A neural network to predict symptomatic lung injury [J]. Phys Med Biol, 1999,44: 2241-2249.

[37] Su Mu, Miften M, Whiddon C,etal. An artificial neural network for predicting the incidence of radiation pneumonitis [J]. Med Phys, 2005,32: 318-325.

[38] Thames HD, Zhang M, Tucker SL,etal. Cluster models of dose-volume effects [J]. Int J Radiat Oncol Biol Phys, 2004,59: 1491-1504.

[39] El Naqa I, Bradley J, Blanco AI,etal. Multivariable modeling of radiotherapy outcomes, including dose-volume and clinical factors [J]. Int J Radiat Oncol Biol Phys, 2006,64: 1275-1286.

[40] Valdagni R, Rancati T, Fiorino C. Predictive models of toxicity with external radiotherapy for prostate cancer: clinical issues [J]. Cancer, 2009,115: 3141-3149.

[41] Deasy JO, El Naqa I. Image-based modeling of normal tissue complication probability for radiation therapy [J]. Cancer Treat Res, 2008,139: 215-256.

[42] Acosta O, Dowling J, Cazoulat G,etal. Atlas based segmentation and mapping of organs at risk from planning ct for the development of voxel-wise predictive models of toxicity in prostate radiotherapy[M]//Prostate Cancer Imaging. Computer-Aided Diagnosis, Prognosis, and Intervention. Berlin Heidelberg: Springer, 2010: 42-51.

[43] Allen Li X, Alber M, Deasy JO,etal. The use and QA of biologically related models for treatment planning: short report of the TG-166 of the therapy physics committee of the AAPM [J]. Med Phys, 2012,39: 1386-1409.

ReviewofNormalTissuesComplicationProbabilityModels

ZHU Jian1,2LI Bao-Sheng1,2SHU Hua-Zhong3*BAI Tong1,2YIN Yong1,2LUO Li-Min3DE CREVOISIER Renaud4

1(DepartmentofRadiotherapy,ShandongTumorHospital&Institute,Jinan250117,China)2(KeyLaboratoryofRadiationOncologyofShandongProvince,Jinan250117,China)3(LaboratoryofImageScienceandTechnology,SoutheastUniversity,Nanjing210096,China)4(LaboratoireTraitementduSignaletdel’Image(INSERM-U1099),UniversitédeRennes1,Rennes35510,France)

To predict the probability of radiotherapy complications, optimize radiotherapy plans and reveal the radio-biological characteristics by normal tissue complication probability (NTCP) models are becoming important issues in the radiation oncology field recently. All of them can be achieved by identifying the NTCP model parameters with clinical and follow-up data. In this work, six NTCP models from literatures, model identification and comparison methods were summarized; three improved NTCP models and some other complication predictive methods were introduced as well. Issues of NTCP in individual radiotherapy were discussed and proposed from the clinical application point of view.

tumor; radiotherapy; complication; predictive model

10.3969/j.issn.0258-8021. 2014. 02.014

2013-09-20， 录用日期:2013-11-20

国家重点基础研究发展计划(973计划)(2011CB707904)； 国家自然基金(81301298)；山东省自然科学基金(ZR2010HQ053)

R318

A

0258-8021(2014) 02-0233-08

*通信作者。E-mail: shu.list@seu.edu.cn