牙齿预备体参数化设计研究与实现

宋英龙 戴 宁* 许 治 孙玉春 吕培军 原福松

1(南京航空航天大学机电学院，南京 210016)2(口腔数字化医疗技术和材料国家工程实验室，北京大学口腔医学院，北京 100081)

牙齿预备体参数化设计研究与实现

宋英龙1戴 宁1*许 治1孙玉春2吕培军2原福松2

1(南京航空航天大学机电学院，南京 210016)2(口腔数字化医疗技术和材料国家工程实验室，北京大学口腔医学院，北京 100081)

牙体预备是牙齿硬组织疾病治疗的关键环节。为开发新的牙齿预备操作模式并实现自动化预备体制备，研究了复杂形状、多约束牙齿预备体模型的计算机生成和参数化修改。首先，针对三角网格模型尺寸约束特点，通过分析模型尺寸链之间的关系，提出了预备体模型生成的参数化操作，通过此操作能够生成全瓷修复标准范围内的预备体模型；同时，利用基于历史的方法实现了预备体模型的参数化动态修改。磨牙和前磨牙各20例预备体参数化实验证明,此算法能够很好地完成预备体模型生成和参数化修改。通过第三方软件Geomagic Studio证实模型设计偏差在48 μm以内，小于100 μm的临床密合精度要求。为改革预备体临床操作模式，研发自动化牙体预备设备打下了坚实的基础。

预备体设计；离散数据建模；参数化CAD；参数化操作

引言

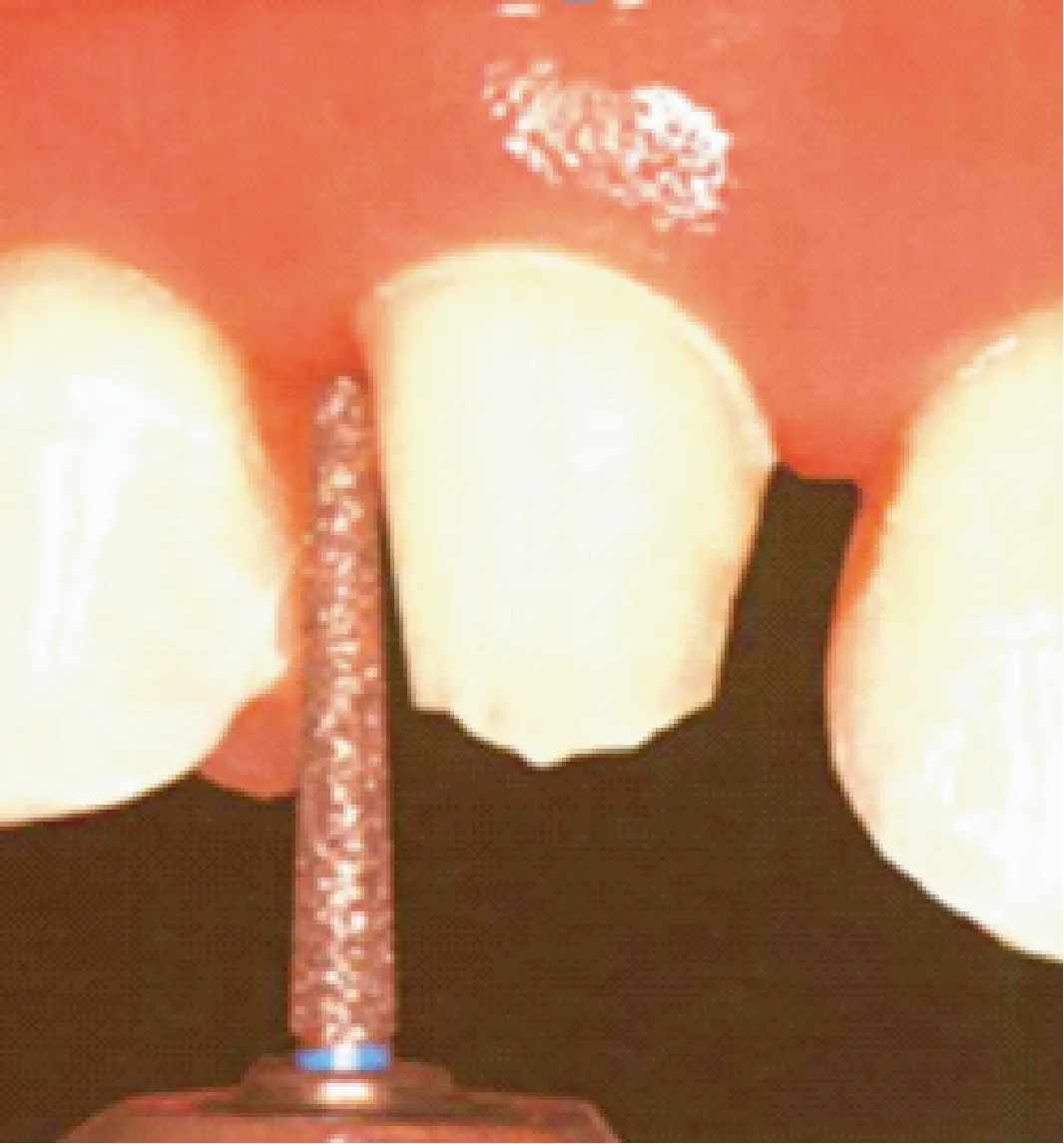
图1 牙齿预备过程Fig.1 Teeth preparation process

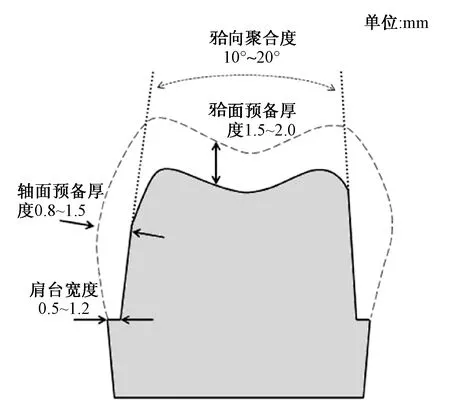
图2 预备体各尺寸约束Fig.2 Preparation dimensional constraints

传统的牙体预备，主要靠医生通过“目测+手控”的方式，利用金刚砂车针进行大量重复、费力的打磨操作。人眼视觉偏差、人手控制误差等很难避免。预备质量不合格造成的牙冠脱落、不能顺利就位、牙龈牙周损伤等问题，严重影响牙齿修复的效果和使用寿命。另据调查，欧美等发达国家专科口腔医生与口腔患者的比例约为1∶500～1∶2 000，而我国却是1∶20 000。系统化、专业化培养一名口腔医师大约需要5～10年时间，这直接导致具有较高临床操作水平的口腔医师严重不足，口腔治疗费用居高不下。因此，如何使牙科医师摆脱传统的超负荷重复性劳动，并且使年轻从业医师和基层口腔医务工作者，也能够快速标准地制作预备体，成为当前亟需解决的难题。计算机辅助设计在口腔医学上的推广应用，给新的牙齿预备操作模式带来了希望。大量研究和实践表明：三维数字化测量和计算机辅助的自动化控制技术，将给传统口腔医学临床操作模式带来新一轮革命。这就需要研究牙齿预备体模型的计算机表示与参数化修改，即利用计算机辅助的方法，生成符合要求且能参数化灵活修改的预备体数字化模型。

预备体模型参数化设计，主要包括两部分内容，首先利用三角网格操作，将牙齿模型设计成符合各项约束指标的预备体形状，然后利用参数化技术实现预备体模型的动态修改。在网格模型操作方面，Bruyns研究了三角网格的裁剪操作[2]；Pernot等研究了网格曲面的补孔算法[3]；Qu等研究了三角网格模型的偏置算法[4]。通过这些模型操作，可以将原始牙齿模型设计成满足各项约束指标的预备体形状。

参数化研究工作最早可追溯到20世纪60年代早期，其参数化模型主要有两种基本的表示形式:基于约束的模型和基于历史的模型[5]。Lin等开创性地提出了求解约束模型的变量几何法[6]，这种方法通用性好，能处理复杂的约束关系，但是盲目求解大规模方程组，求解复杂度高且解值存在二义性；Fudos等研究了基于图的求解方法[7]，这种方法速度快，且能判断模型过约束和欠约束情况，适合约束规模较小的模型求解。基于历史的模型顺序描述一个几何体的构造过程，将构造操作按顺序生成一个计划列表，当参数值改变时构造历史被重新执行以更新几何图形。这种方法顺序相对固定，因此在灵活性方面有所欠缺，Monedero等对此有详细的研究[8]。参数化在计算机辅助设计(Computer aided design,CAD)中的应用节省了大量重复劳动，在设计的灵活性和系列化方面取得了良好的效果。

1 预备体参数化设计流程

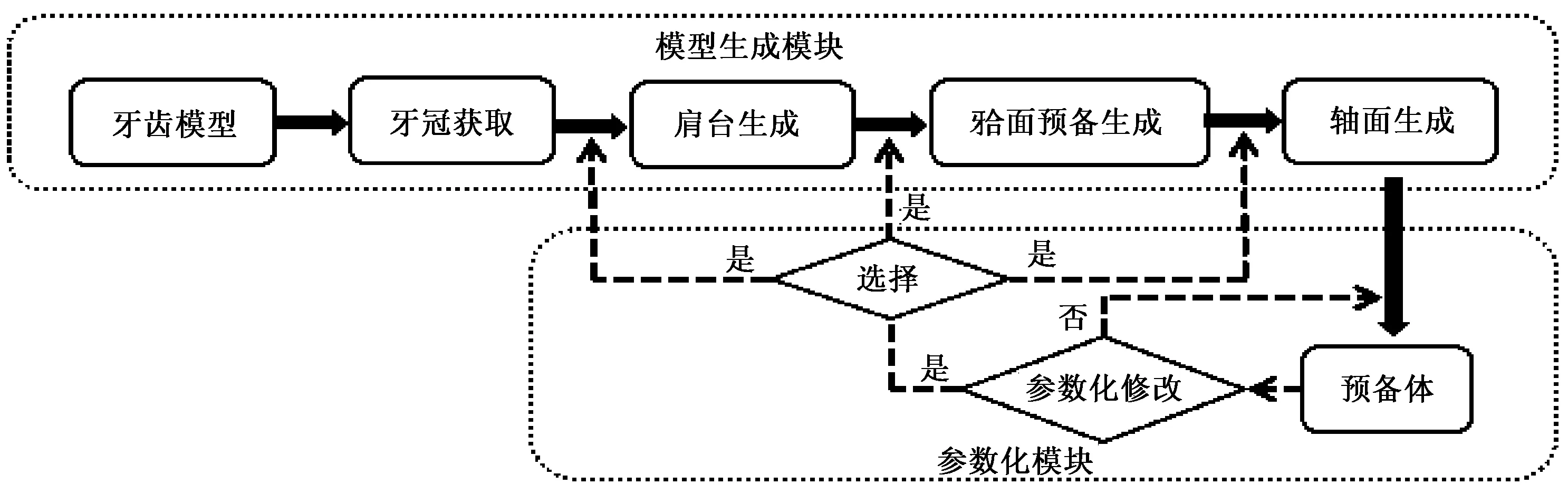
图3 预备体模型生成及参数化更新流程Fig.3 Preparation model generation and parametric design workflow

2 基于参数化操作的模型生成

参数化操作法是在建立图形拓扑约束关系的基础上，采用参数化操作表示与处理几何约束，并通过与参数化操作相对应的几何计算程序，逐步确定出精确几何模型的方法[9]。其构造过程可被看作是受操控的构造历史，记录为序列或树的形式，其中重要的是按照操作顺序单向的依赖关系。对于三角网格模型来说，参数化操作有裁剪、偏置和补孔等。参数化操作法简单、实用，能够很好地实现预备体模型的构造生成。

2.1预备体模型尺寸约束分析

预备体模型是三角网格模型属于离散数据表示，它与常见的连续曲面模型在表示上有一定差异(见图4)。三角网格模型是由离散点和三角片组成，网格边界只能保证位置连续，而连续曲面模型却可以做到边界的一阶或高阶导数连续。

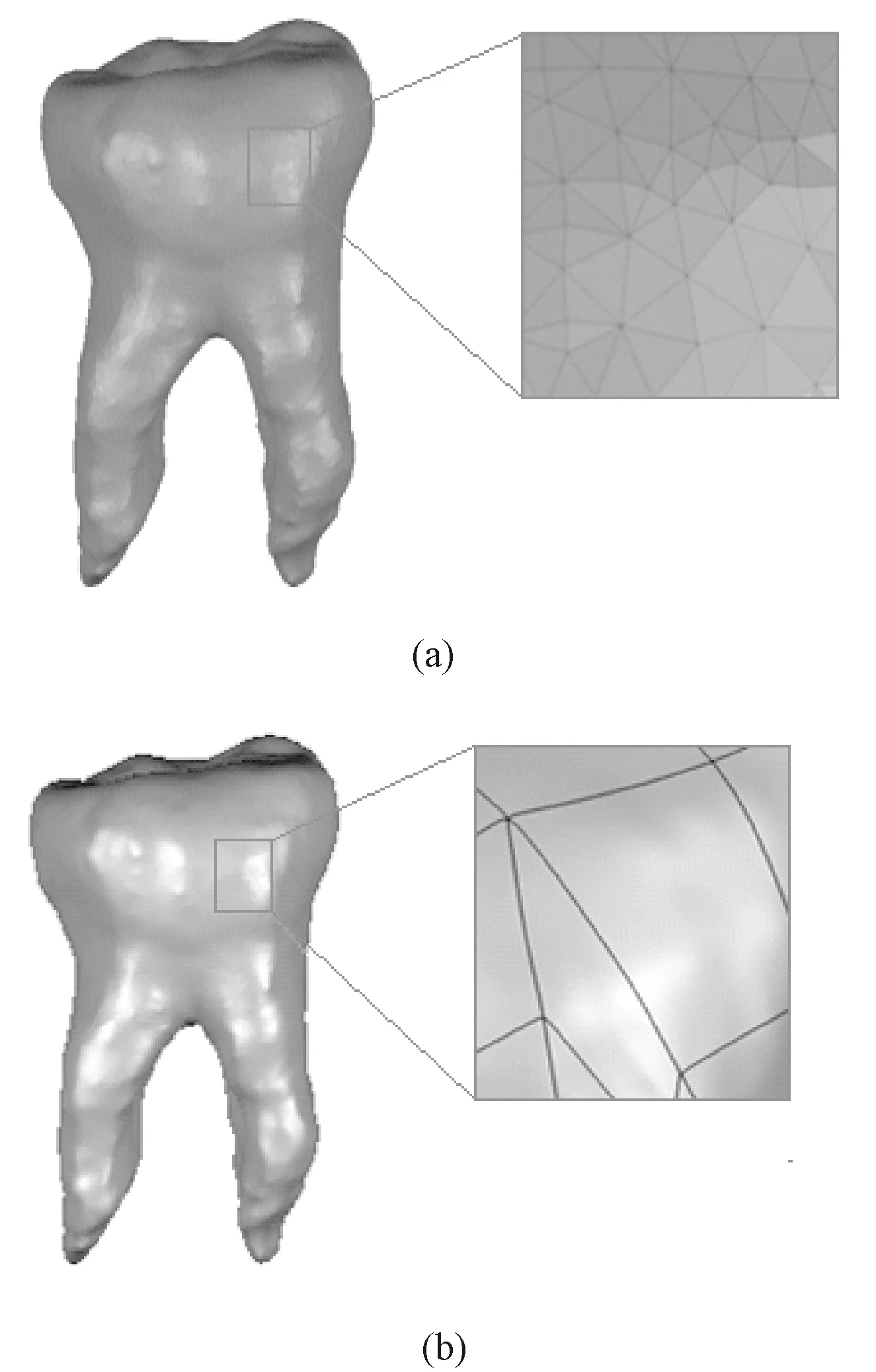
图4 三角网格模型与连续曲面模型表示方式的区别。(a)三角网格模型；(b)连续曲面模型Fig.4 The difference of triangular model and continuous model. (a) triangular model;(b) continuous model

三角网格模型的表示方式决定了其在尺寸约束方面的特殊性，具体有以下两个方面。

(1) 尺寸的亚约束(弱约束)性

由于三角网格模型的边界不是严格意义上的曲线，而是由很多的折线段组成。同时由于模型的微小变形等影响，模型长度尺寸和角度尺寸并不是在各处严格相等的，而是在一定区间内波动，即预备体模型的长度尺寸d实际为d±Δd，见图5。

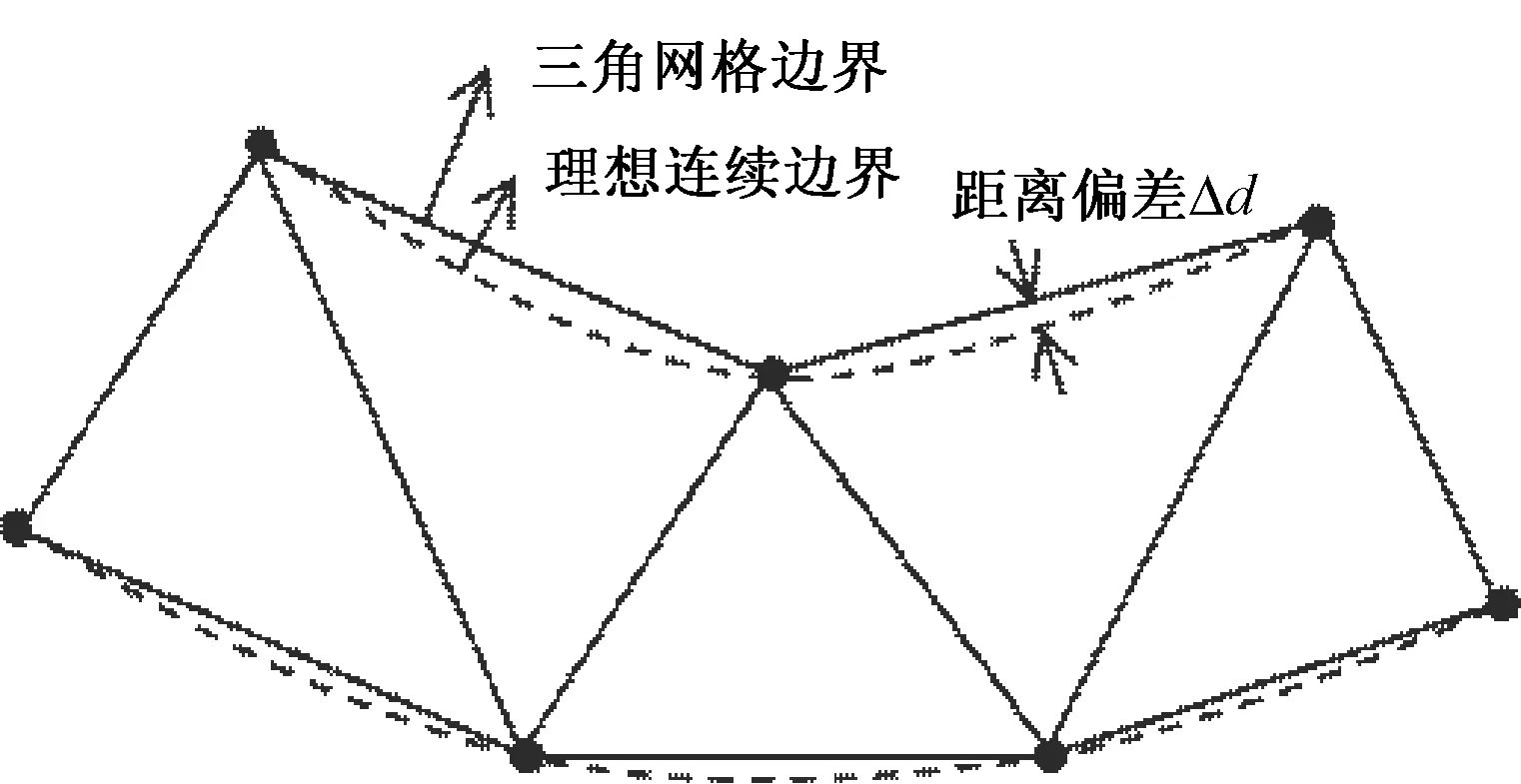
图5 三角网格模型长度尺寸的亚约束性Fig.5 Sub-binding of triangular mesh length dimension

同样，角度尺寸α实际为α±Δα，见图6。

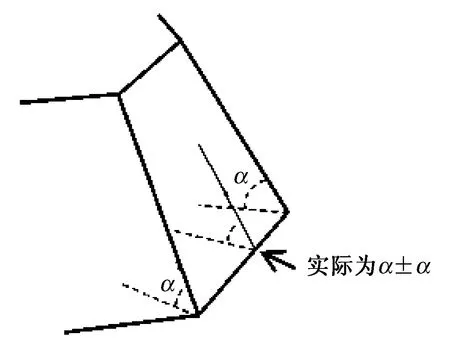
图6 三角网格模型角度尺寸亚约束性Fig.6 Sub-binding of triangular mesh angle dimension

(2)聚合度约束的微分性

由于三角网格模型边界从连续曲线离散成一系列点和折线段的组合，因此，其聚合度不能像连续曲面模型那样保证角度的连续一致性，只能保证其在离散点处符合要求。聚合度约束受模型精度即三角片边长大小的影响，边长折线越短，约束精度越高，见图7。

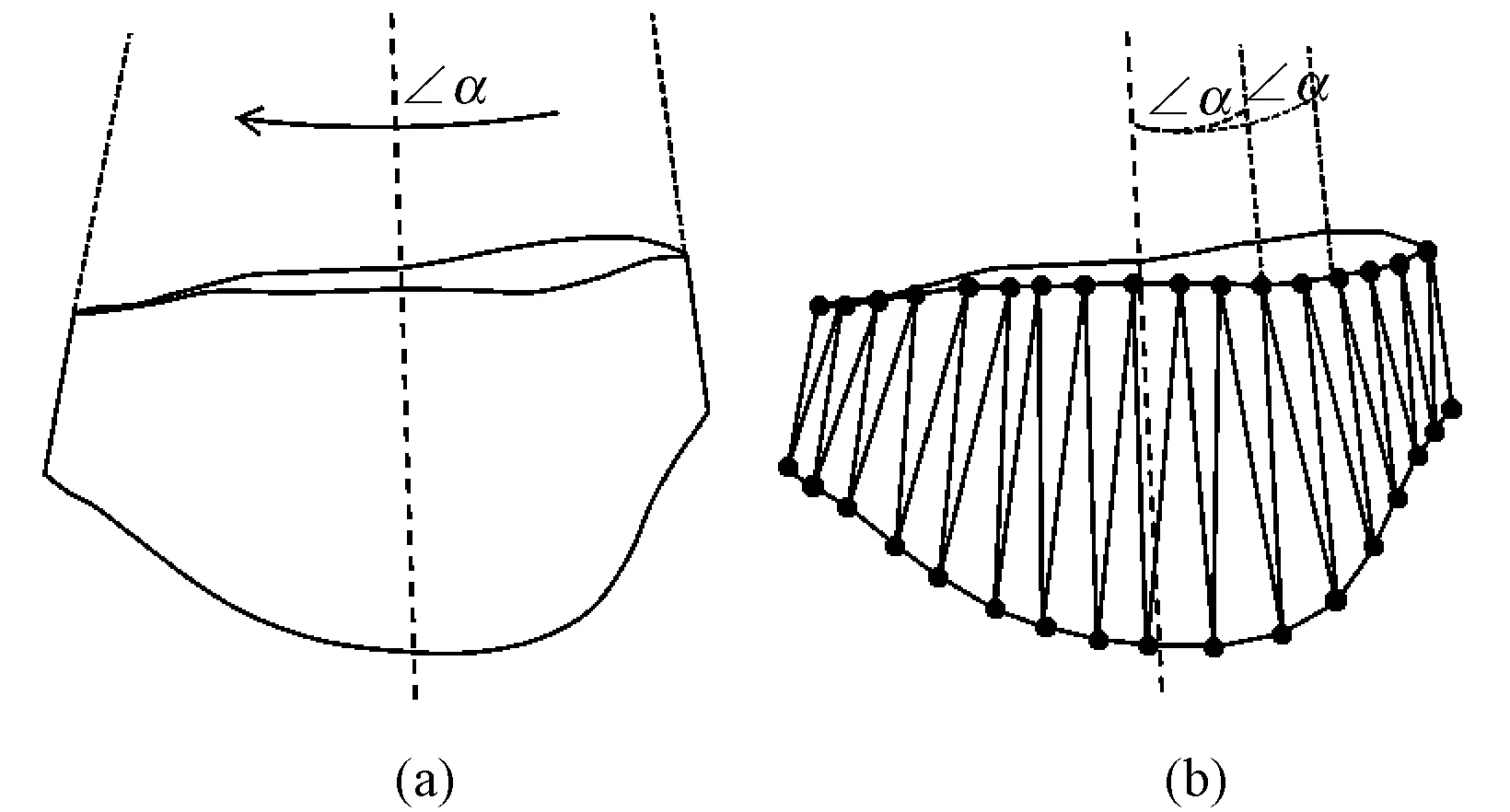
图7 角度约束的微分性。(a)连续模型；(b)三角网格模型Fig.7 The differential character of angle constraint. (a) Continuous model;(b) Triangular model

2.2预备体模型尺寸链约束分析

由图示分析各方向尺寸链关系，可得到尺寸参数关系式方程组如下：

(1)

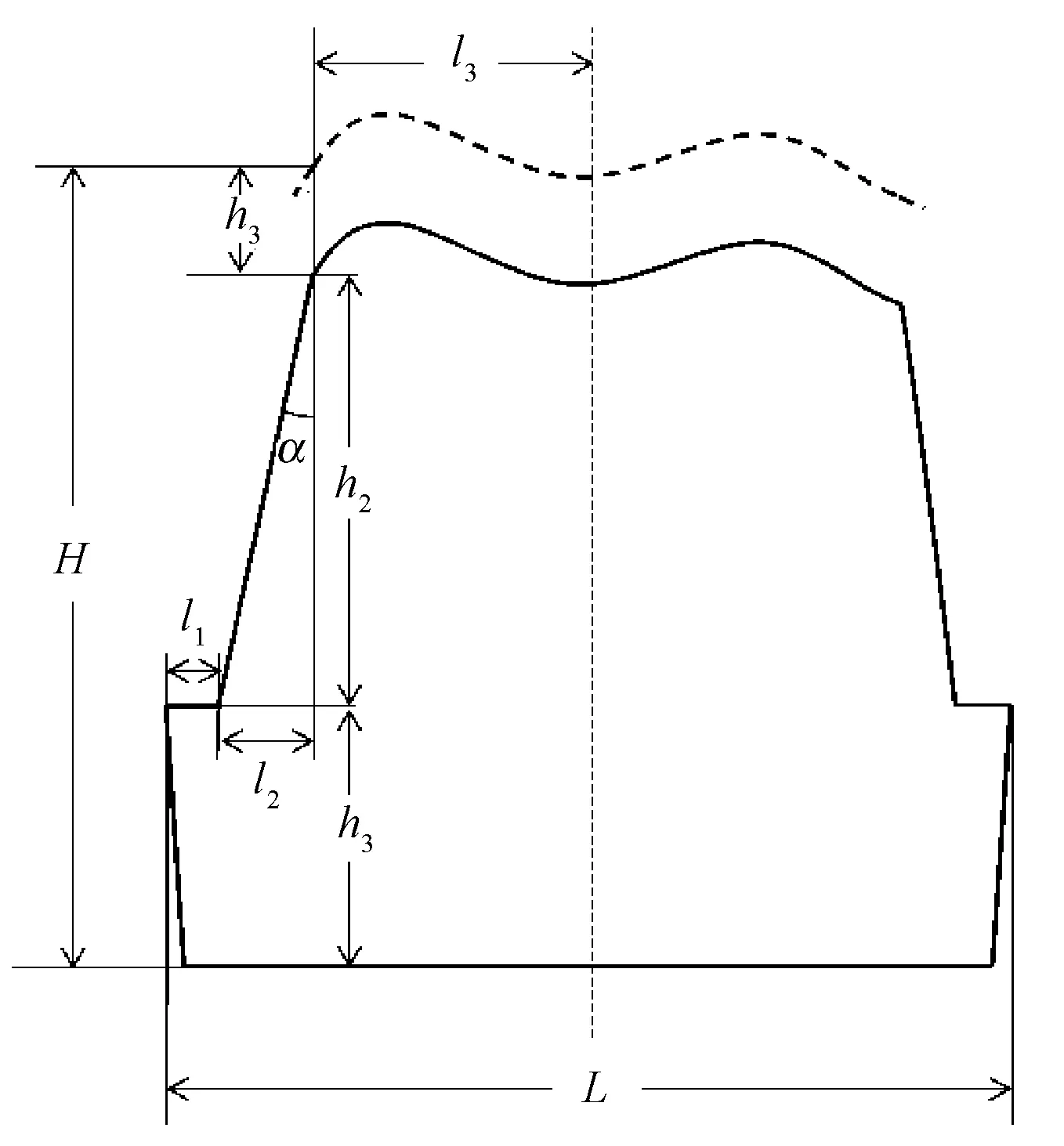
图8 预备体颊舌向截面示意Fig.8 Preparation sectional view in buccolingual direction

对于完整预备体，n=3，m=2，其中，l1、h1、α为参数化的3个参数值，对于特定牙齿，H、L和h3为固定值。当参数值给定时，方程组为含有3个未知数(即l2、l3、h2)的方程组，由已知的3个方程可以唯一确定一组l2、l3、h2的值，从而模型各部分尺寸确定，模型既不过约束也不欠约束，模型完备自由度为0。

2.3参数化操作预备体设计

预备体尺寸链约束分析证明了模型约束的可解性，此时可将模型设计步骤对应成参数化操作，主要的参数化操作包括4个步骤。

步骤1：牙冠模型获取。牙齿预备过程主要处理龈缘线以上部分即牙冠部分，在初期的研究中假定颈部边缘线与龈缘平齐。利用手工半自动提取的牙龈边缘线将CT获取的牙齿模型分隔开，形成牙冠部分模型和牙颈牙根部分模型。

步骤2：预备体直角肩台生成。预备体肩台为均匀宽度的环形平面，肩台宽度为主要的几何约束。在此执行参数化偏置操作来生成肩台几何特征，即将分割后的牙冠模型利用基于点的模型偏置算法逐点偏置肩台宽度距离，然后缝合牙冠模型和牙颈牙根模型间的缝隙生成肩台平面。

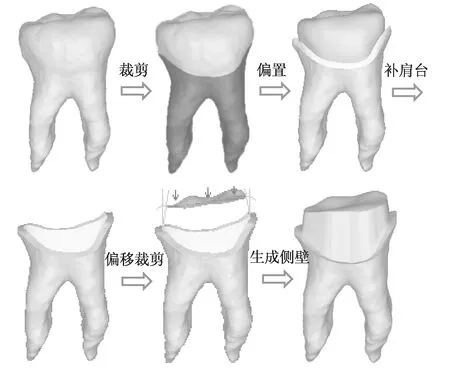
图9 参数化操作预备体模型生成Fig.9 Parametric operations of preparation model generation

3 基于历史的模型参数化更新

在参数化模型表示中，基于约束的模型直观、形象、通用性好，但较为适用约束规模较小的模型，如二维轮廓模型等。在三维模型中由于各种点、线等几何实体大量增加，约束关系呈非线性增长，使得约束复杂度大大增加，求解约束过程变得越来越困难。基于历史的模型，侧重于模型生成的历史，简单、实用，但由于需要严格遵守某种构造顺序，因此柔性和灵活性较差[8]。考虑到预备体模型生成已经具体为各种参数化操作步骤，顺序相对稳定，恰好适合基于历史的参数化，因此采用基于历史的方法实现预备体的参数化修改。其技术方案如下：参数化操作和参数值一起按照模型构造顺序被记录下来，并为每个操作附上标记。当参数尺寸修改时，找到对应标记的操作并以此开始按照构造历史，以新的参数值重新构造模型，完成模型的更新。具体流程如图10所示。

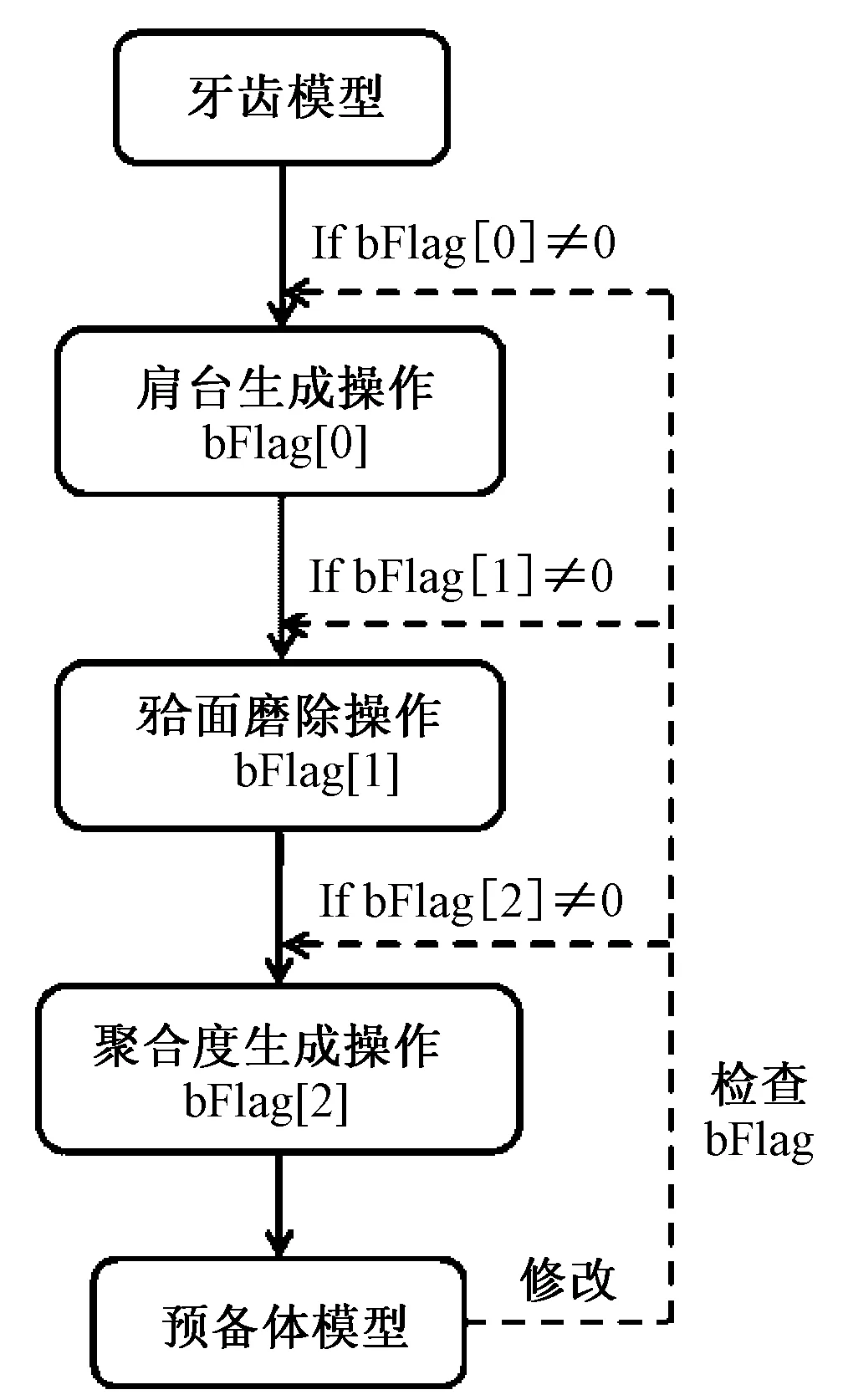
图10 基于历史的参数化更新Fig.10 History-based parameterization

4 结果

4.1算法实例及运行时间

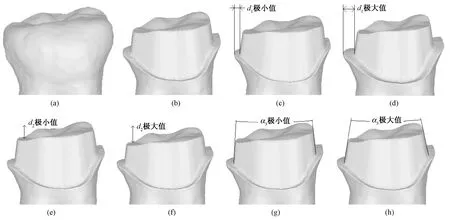
图11 第一磨牙参数化建模实例。(a)牙齿模型;(b)中间值d1=0.85, d2=1.75, α3=15; (c)d1=0.5, d2=1.75, α3=15;(d) d1=1.2, d2=1.75, α3=15; (e)d1=0.85, d2=1. 5, α3=15; (f) d1=0.85, d2=2.0, α3=15; (g) d1=0.85, d2=1.75, α3=10; (h) d1=0.85, d2=1.75, α3=20Fig.11 Results of first molar parametic modelling. (a) Teeth model; (b) Middle value d1=0.85, d2=1.75, α3=15; (c) d1=0.5, d2=1.75,α3=15;(d) d1=1.2, d2=1.75, α3=15;(e) d1=0.85, d2=1.5, α3=15;(f) d1=0.85,d2=2.0, α3=15; (g) d1=0.85, d2=1.75, α3=10; (h) d1=0.85,d2=1.75, α3=20

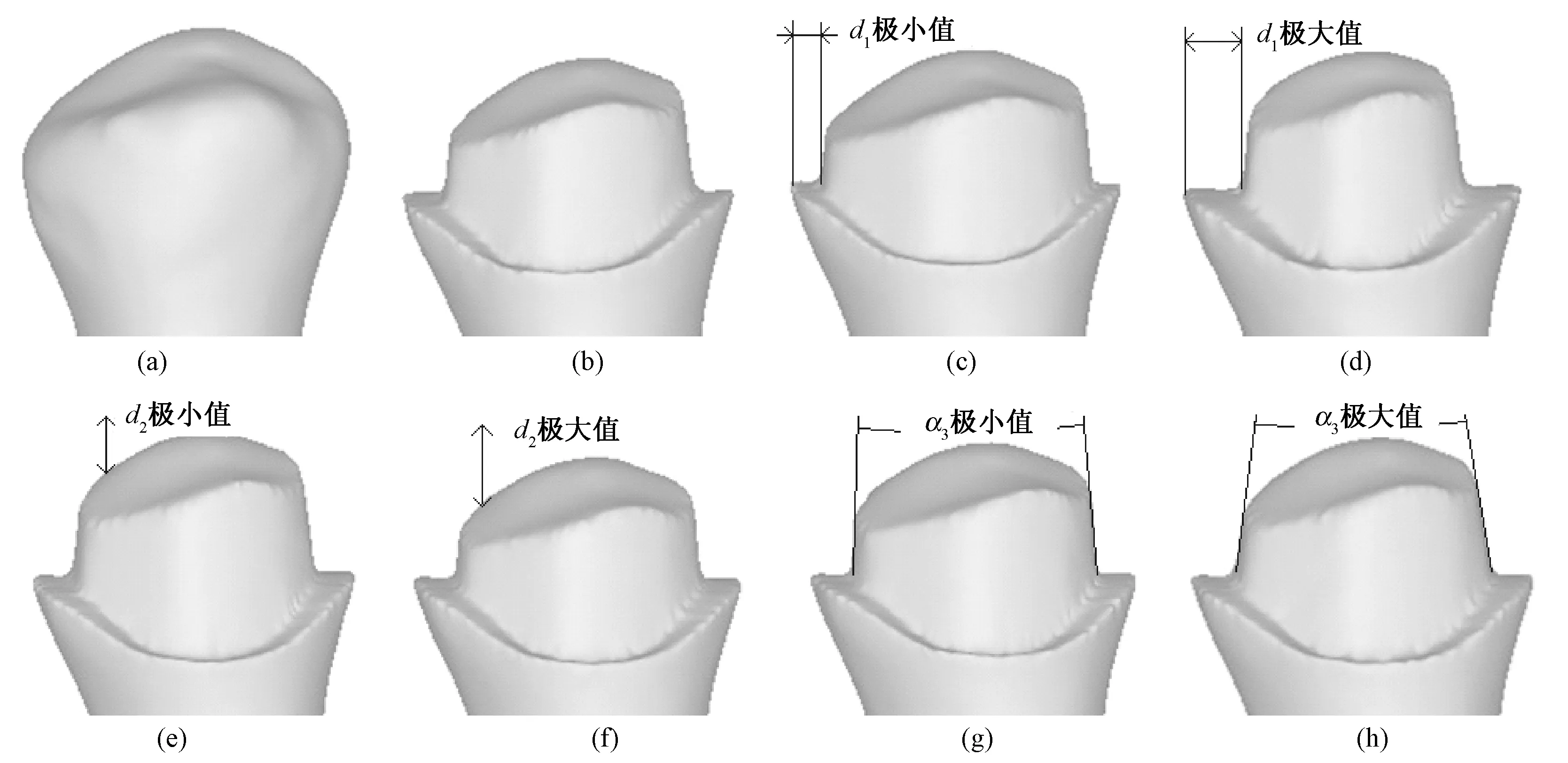
图12 第二前磨牙参数化建模实例。(a)牙齿模型; (b)中间值d1=0.85, d2=1.75, α3=15; (c)d1=0.5, d2=1.75, α3=15; (d)d1=1.2,d2=1.75, α3=15; (e)d1=0.85, d2=1. 5, α3=15; (f) d1=0.85, d2=2.0, α3=15; (g) d1=0.85, d2=1.75, α3=10; (h) d1=0.85, d2=1.75, α3=20Fig.12 Results of second premolar parametic modelling. (a)Teeth model; (b)Middle value d1=0.85, d2=1.75, α3=15; (c)d1=0.5, d2=1.75, α3=15;(d) d1=1.2, d2=1.75, α3=15;(e) d1=0.85, d2=1. 5, α3=15;(f) d1=0.85, d2=2.0, α3=15;(g) d1=0.85, d2=1.75, α3=10; (h) d1=0.85,d2=1.75, α3=20

表1预备体建模时间和参数精度(均值标准差)

Tab.1Preparationmodelingtimeandparametersaccuracy(meanSD)

类型分组样本量/个建模时间/s肩台偏差/μm聚合度偏差/(°)磨牙组204 85±0 695 00±0 290 44±0 05前磨牙组201 43±0 215 50±0 820 52±0 11

4.2精度分析

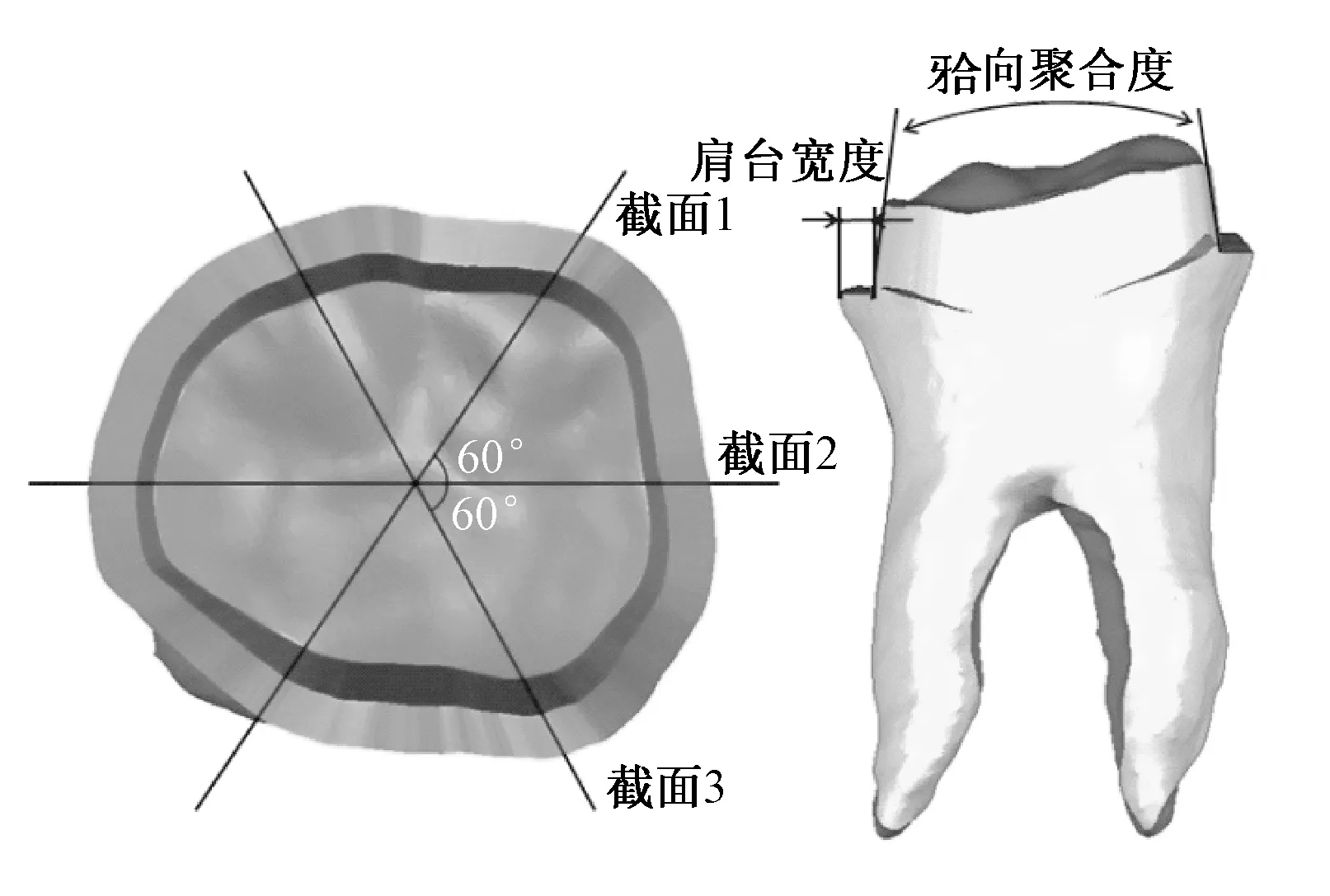
图13 精度分析截面位置与剖面图Fig.13 Cross-sectional position and view of precision analusis

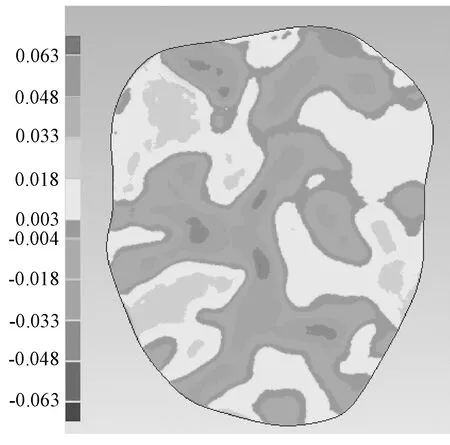
图14 牙齿、面偏差色斑图Fig.14 Deviation mottling of tooth occlusal surface

5 讨论与结论

本研究首次尝试对复杂形状、多约束的牙齿预备体进行数字化、参数化建模。针对离散网格模型的特殊性，在分析尺寸约束关系的基础上，通过借鉴连续曲面的参数化方法，将预备体模型设计分解成连续步骤的参数化操作，解决了预备体模型的精确生成问题。同时，利用基于历史的参数化方法，结合参数化操作步骤，成功解决了预备体模型的参数化修改问题，具有较传统手工预备方法更高的精度和手术效率，为开发新的牙齿预备临床操作模式，研发新的自动化预备设备打下了坚实的基础。同时也验证了基于参数化操作和基于历史方法在模型参数化过程中的技术可行性，对于其他离散模型参数化建模也具有重要的参考意义。

[1] 夏刚，刘晓亮.第三次全国口腔健康流行病学调查报告[R].北京：人民卫生出版社,2008.

[2] Bruyns CD,Seager S,Menon A,etal.A survey of interactive mesh- cutting techniques and a new method for implementing generalized interactive mesh cutting using virtual tools[J].The Journal of Visualization and Computer Animation , 2002,13: 21-42.

[3] Pernot JP,Moraru G,Veron P.Filling hole in meshes using a mechanical model to simulate The curvature variation minimization[J].Computers Graphics , 2006,30:892-902.

[4] Qu Xiuzhi,Stucker B. A 3D surface offset method for STL-format models [J].Rapid Prototying Journal,2003,9(3):133-141.

[5] 孟祥旭,徐延宁.参数化设计研究[J].计算机辅助设计与图形学学报, 2002 ,14(11):1086-1090.

[6] Lin VC,Gossard DC,Light RA.Variational geometry in computer-aided design[J]. Computer Graphics,1981,15(3):171-177.

[7] Fudos I, Hoffmann CM. A graph-constructive approach to solving systems of geometric constraints[J]. ACM Transaction on Graphics, 1997,16(2):179-216.

[8] Monedero J. Parametric design:a review and some experiences[J]. Automation in Construction,2000,9:369-377.

[9] Bettig B,Hoffmann CM.Geometric constraint solving in parametric computer aided design[J].Journal of Computing and Information Science in Engineering,2011,11:211-218.

[10] 刘荣森.全瓷修复的牙体预备[J].中华老年口腔医学杂志, 2009,7(3):177-179.

[11] 郭大伟.粘结全瓷冠的牙体预备设计要求[J].口腔材料器械杂志,2003,12(3):157-159.

ResearchandImplementationforParametricDesignofToothPreparation

SONG Ying-Long1DAI Ning1*XU Zhi1SUN Yu-Chun2LV Pei-Jun2YUAN Fu-Song2

1(CollegeofMechanicalandElectricalEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)2(NationalEngineeringLaboratoryforDigitalandMaterialTechnologyofStomatology,PekingUniversitySchoolandHospitalofStomatology,Beijing100081,China)

Tooth preparation is a key part in the treatment of dental hard tissue disease. In order to develop a new mode of tooth preparing operation and realize automatic preparation, in this paper, we studied the computer aided method of complex-shaped and multiple-constrained preparation generation and parametric modification. First, for the characterization of triangular mesh, we proposed parametric operations of preparation generation by analyzing the relationship of dimension chains. By the operations, an whole-ceramic preparation model within the standard was generated. Meanwhile, a history-based approach was used to realize the preparation’s dynamic modification. Twenty instances of molar and premolae showed that our method worked well in preparation’s generation and parametric modification. The model was conformed with maximum design deviation of 48 μm by the third-party software Geomagic Studio, reaching the clinical adhesion requirement of less than 100 μm.

preparation design; discrete data modeling; parametric CAD; parametric operation

10.3969/j.issn.0258-8021. 2014. 01.011

2013-05-16，录用日期：2013-12-30

国家科技支撑计划(2012BAI07B04)；国家自然科学基金(51205192,81271181)；南航科研基地创新基金(NJ20130015)

R318

A

0258-8021(2014) 01-0071-08

*通信作者。E-mail: dai_ning@nuaa.edu.cn