10岁儿童头部有限元模型的建立及验证

曹立波 周 舟 蒋彬辉 张冠军

(湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082)

10岁儿童头部有限元模型的建立及验证

曹立波 周 舟 蒋彬辉*张冠军

(湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082)

运用ANSYS ICEM CFD以及HYPERMESH软件对10岁儿童头部几何模型进行合理的网格划分，获得具有高度解剖学细节的10岁儿童头部有限元模型。利用MADYMO软件自带的假人，模拟一起典型跌落事故中,受伤儿童从3个不同高度跌落时人体的动力学响应过程，并计算头部与地面碰撞接触瞬间的方位和速度等运动学参数。然后将这些参数输入到10岁儿童头部有限元模型中，模拟头部与地面的碰撞过程，并分析与损伤相关的生物力学参数。结果表明，颅骨的最大应力和最大应变分布在枕骨右侧，与碰撞点的位置较为吻合，但均未超过颅骨的耐受极限。利用颅内压力可较好地预测脑组织的损伤程度，而利用脑组织的von-mises应力可较好地判断脑组织的损伤位置。事故重建的结果表明,该模型具有较好的生物逼真度，可以用于儿童头部损伤生物力学的研究。

头部损伤；有限元模型；事故重建；10岁儿童

引言

随着我国乘用车逐步进入家庭，儿童乘员的数量也在不断增加。通过对交通事故中儿童受伤情况的调查研究发现，道路交通事故导致的儿童伤害和死亡率,在1985～1999年的15年间增长了81%[1]，青少年头部撞击损伤的发生率更是高达38.76%[2]。儿童时期所遭受的头部损伤可能导致持续一生的精神损害，造成严重的社会和经济损失。因而，儿童颅脑损伤机理的研究及相关防护装置的开发，成为近期的研究热点。

头部损伤生物力学的主要研究手段，有机械模型实验、动物模型实验、志愿者实验及尸体模型实验。机械模型实验具有较好的重复性，也便于实验数据的测量。但是机械模型的生物逼真度有限，难以代替生物实验。动物实验可以观察到由于承受载荷而引起的组织破坏及病理生理学变化，但动物与人在解剖结构和组织材料特性上存在较大的差异，且在发育速度上也存在很大的区别。因此在利用动物实验来研究儿童损伤时，除了需要处理动物与人体在解剖结构和材料特性上的差异外，还须关联动物与人在发育速度上的关系。志愿者实验是获得最真实人体生物力学响应数据的方法，但在实验过程中志愿者存在一定的损伤风险，这使得志愿者实验广受批评和制约。尸体具有与活体相同的解剖结构，是开展损伤生物力学研究较好的替代品。但由于社会、伦理和法律等方面的限制，尸体标本的获得受到了很大的限制，特别是儿童尸体实验更是难以开展[3]。

近年来，随着计算机技术和软件能力的不断提高，数字化仿真技术取得很大的进展，有限元模型逐渐成为研究儿童头部损伤的重要手段。有限元模型可重复使用，并且能用于颅脑应力、应变及其他各种相关特征参数的研究。然而，由于缺乏儿童颅脑的材料属性和损伤极限数据，已经建立的非婴幼儿的儿童头部有限元模型非常有限。2007年Roth等建立了3 岁儿童头部模型，用以研究真实事故中儿童跌倒导致的神经损伤阀值[4]。2012 年Ruan等构建了一个比较详细的6 岁儿童头部有限元模型，模型的仿真结果经过有效性分析和与Nahum尸体实验数据[5]对比，证明该模型可用于儿童颅脑损伤的基础研究[6]。此外，本课题组在2013 年建立了一个3 岁儿童头部模型，该模型基本能够预测 3岁儿童头部骨折，可用于颅骨骨折损伤机理和耐受限度的研究[7]。

虽然这些模型对儿童颅脑损伤的研究起到了很大的帮助，但它们都集中分布在3～6 岁区间，难以用于其他年龄段儿童头部损伤的研究。因此，本研究构建了一个具有详细解剖学特征的10 岁儿童头部有限元模型，通过对典型跌落事故的重建，保证所建立的模型具有足够的生物逼真度。

1 有限元模型与研究方法

1.1头部有限元模型的建立

模型的解剖学数据，来源于美国密歇根儿童医院一名年龄为10岁的儿童病人临床CT和MRI扫描数据。该儿童性别男，身高为137 cm，且临床诊断记录显示无颅脑损伤。临床数据的最小精度为256像素×256像素，扫描间距为2 mm。其后，采用Mimics(13.0, Materialize, Leuven, Belgium)软件对组织结构进行识别，通过阀值化操作控制各组织的清晰度，获得10岁儿童头部的CAD模型。在此基础上，采用ANSYS ICEM CFD/HEXA(12.0, ANSYS, Canonsburg PA, USA)以及HYPERMESH(10.0, Altair, Troy MI, USA)软件，对几何模型进行前处理和网格划分，建立了相对完整的、具有详细解剖学特征的10岁儿童头部有限元模型。整个模型包括头皮、颅骨、面骨、下颌骨、脑镰、脑幕、脑脊液(集合软脑膜和蛛网膜)、硬脑膜、大脑、小脑、脑干和胼胝体等结构，如图1所示。

模型包括195 290 个节点，23 346 个壳单元和174 910 个6面体单元。参照Dekaban等在统计儿童头部测量学数据时描述的方法[8]，测量头部模型中枕后隆突点到眉间点距离为头长、经过耳部上缘水平的最大宽度为头宽、经眉弓上方突出部绕经枕后结节一周的长度为头围、颅腔的容量为颅容量，并与Dekaban等统计的人体测量学统计数据进行了对比，结果如表1所示：其几何尺寸偏差小于2%。表明该模型基本能够反映10岁儿童头部的几何特点，可用于进一步的有限元建模。

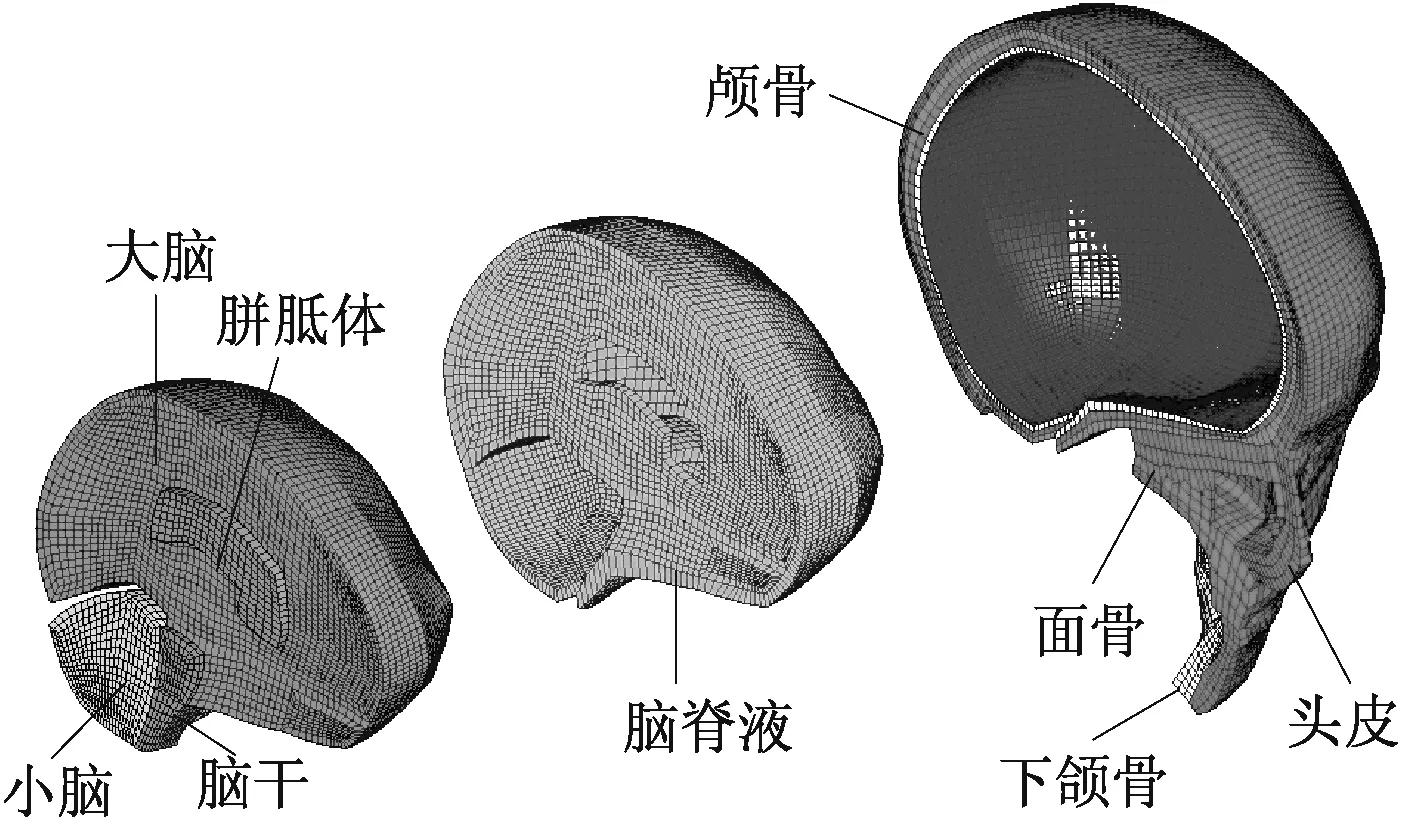
图1 10岁儿童头部有限元模型Fig.1 FE model of the 10 year-old child

表1头部几何尺寸

Tab.1Geomitericparametersofthehead

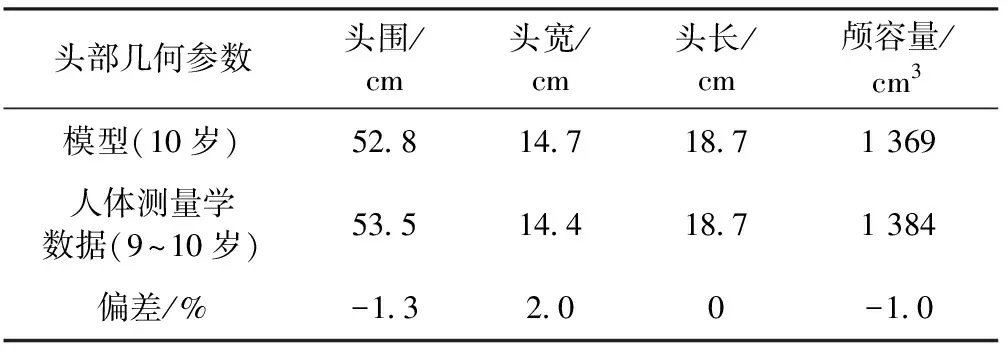
头部几何参数头围/cm头宽/cm头长/cm颅容量/cm3模型(10岁)52 814 718 71369人体测量学数据(9～10岁)53 514 418 71384偏差/%-1 32 00-1 0

建模过程中，脑镰、脑幕、硬脑膜以及一些接触面等采用壳单元模拟，其余组织均采用6面体单元模拟。由于目前还没有完全合适的颅—脑边界条件的接触算法[9]，所以该模型的脑组织通过构建一层脑脊液单元与颅骨连接，且网格连续。

为了确保模型计算过程中，颅骨以及颅内软组织的应力应变不会由于网格质量差而导致较大偏差，在模型网格划分时对网格质量进行了控制，见表2。实体单元中雅克比小于0.7的单元仅占总单元数的2%。

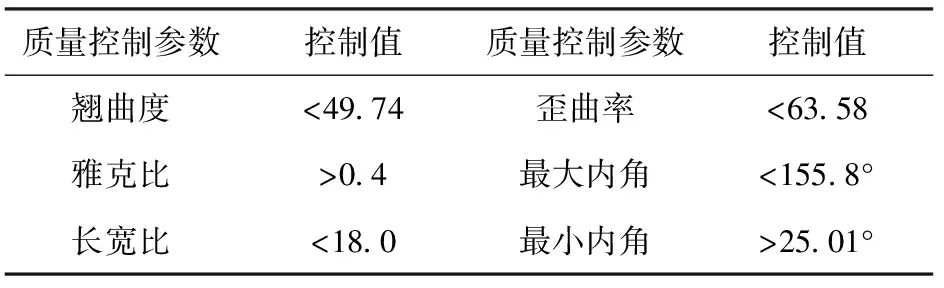
表2 模型网格划分的单元质量控制

1.2头部模型材料参数

由于临床医学数据精度较低，因此难以获得清晰的松质骨和皮质骨的边界，因此参考Motherway等提出的处理方法[10]，参照具有3层结构颅骨的力学特性，将模型中的3层颅骨单元赋予相同的材料。文献检索表明，目前全世界仅有5项研究利用儿童尸体样本测试儿童头部组织的力学材料特性(Davis等，2012[11]；Prange等，2004[12]；Margulies等，2000[13]；Weber等，1985[14]；McPherson等，1980[15])，其中仅有Davis等的研究对象为6周岁的非婴幼儿。由于缺少专门研究10岁儿童颅骨力学性能的实验，模型中颅骨的材料属性是通过缩放的方法得到(见表3)，缩放区间根据文献[11]及文献[16]确定。

表3 颅骨材料属性

脑组织和脑脊液属于生物体软组织，具有质软易变形、抗拉强度非线性及不能抗弯和抗压等特点，通常采用黏弹性材料模型模拟。在参考文献[17]的基础上，10岁儿童头部有限元模型的脑组织和脑脊液的体积弹性模量设定为2.19 GPa，并对脑干和脑脊液等黏弹性结构的剪切模量取值不同。剪切弹性模量可表示为

(1)

式中，G∞为长效剪切模量，G0为短效剪切模量，β为延迟系数，t为时间。具体的取值见表4。

模型中脑镰、脑幕、硬脑膜及头皮的材料参数，是参考文献[17]设定的，具体见表5。

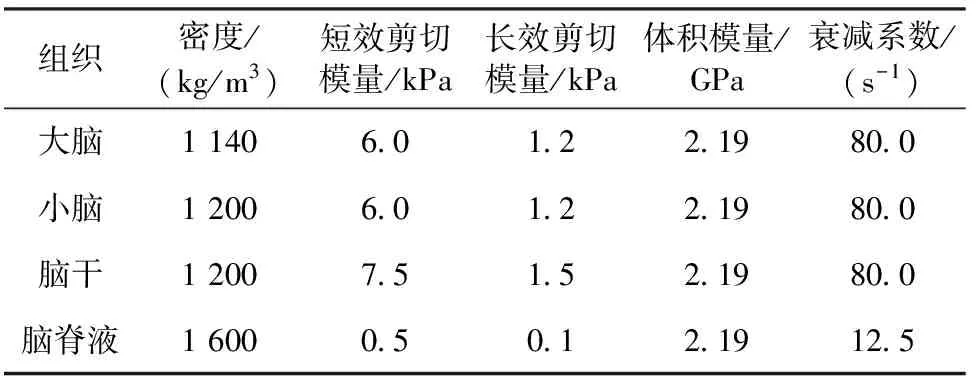
表4 大脑、小脑、脑干及脑脊液材料属性

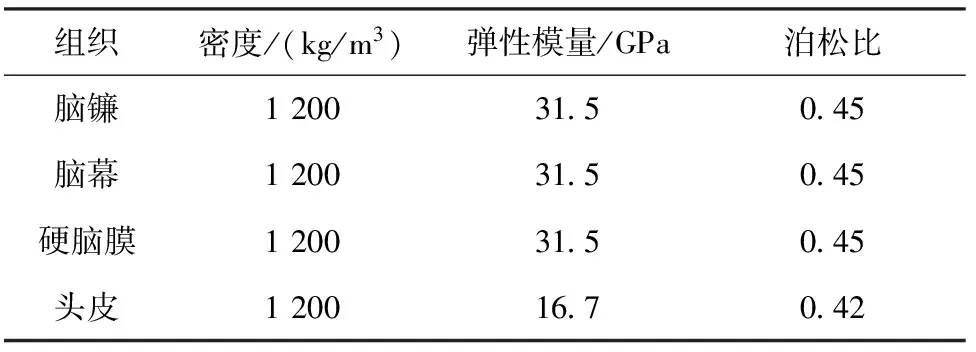
表5 脑镰、脑幕、硬脑膜及头皮材料属性

1.3模型验证

儿童并不是矮小的成人，儿童头部的几何形状、颅骨的连接及骨质结构、器官的材料属性等方面都异于成年人，因此难以借助成年人尸体实验的数据对所建模型进行验证，但目前文献中有关儿童尸体碰撞的实验数据又鲜有发表。国外研究人员将深入的事故调查和事故重建工作的成果，用于有限元模型的验证、损伤评估和损伤机理的研究。本研究运用MADYMO(7.4.1, TNO, Rijswijk, Netherlands)建立一起10 岁儿童跌落事故的再现模型，获得儿童头部与地面发生碰撞过程中的动力学响应，并将碰撞前瞬间头部的运动速度作为有限元模型分析的输入条件，在LS-DYNA(971, LSTC, Livermore, CA, USA)软件中进行仿真计算，最终获得10 岁儿童头部在典型跌落事故中的生物力学响应过程。具体流程见图2。

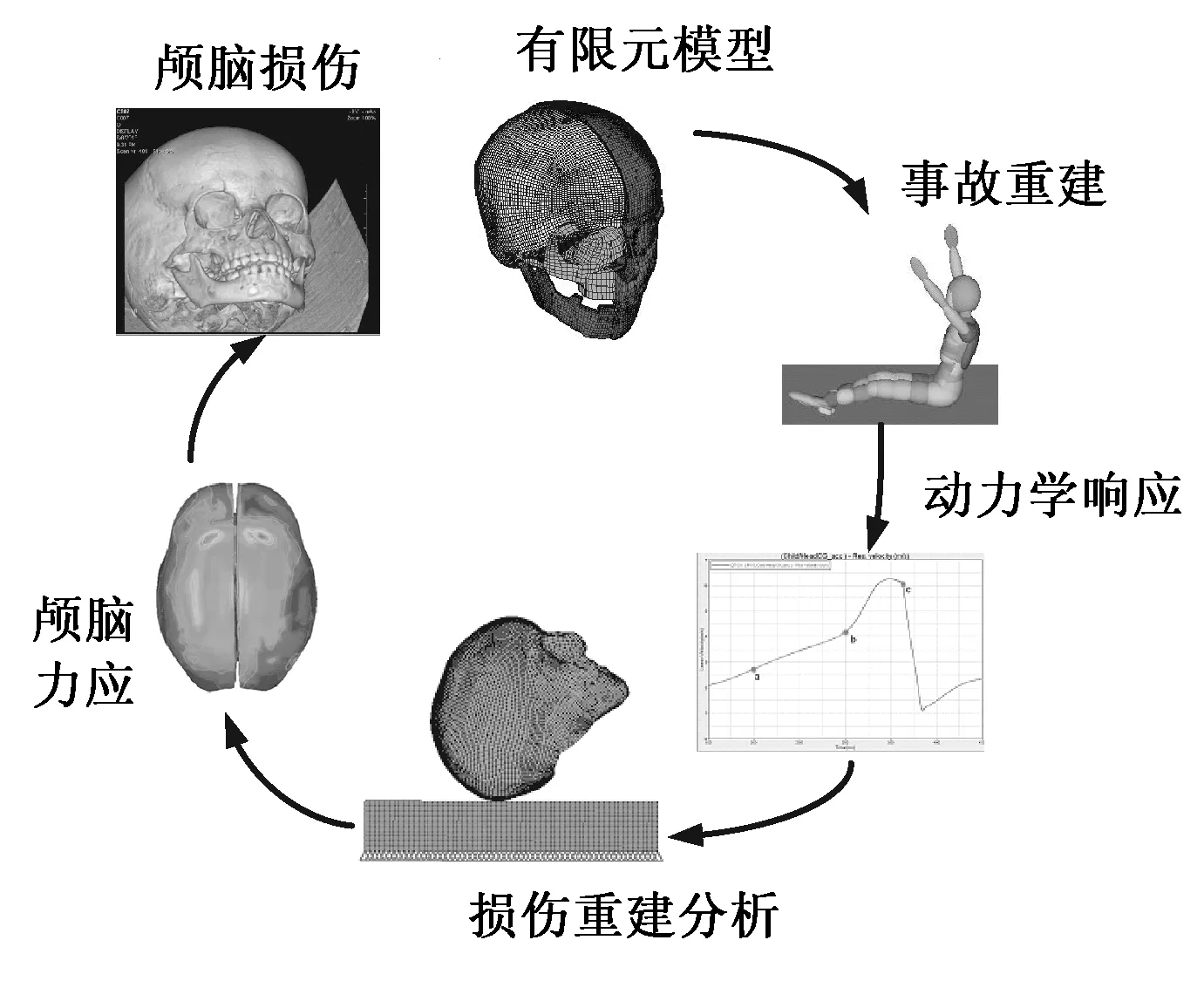
图2 儿童典型跌落事故重建及损伤分析过程图Fig. 2 Accident reconstruction process of a typical fall accident

1.3.1事故重建

选择Plunkett等统计的一起10岁儿童低空跌落事故进行事故，重建及有限元仿真分析。事故描述为一名10 岁儿童在秋千向前摆至最高处时与秋千脱离，从0.9～1.5 米高处跌落，后脑撞击到沥青地面上。CT检查显示伤情为：右顶叶及额叶交界处出现硬脑膜下血肿，伴有颞叶沟回疝等病症。伤者在血肿切除手术后第6 d死亡。尸检报告显示：受害者右顶叶蛛网膜下腔血管畸形，相邻区域仍有少量残余硬脑膜下出血，脑部出现了水肿及脑疝等症状，未发现颅骨骨折[18]。

利用MADYMO软件建立儿童跌落事故再现模型。采用MADYMO软件中的10岁儿童假人，并根据事故描述，设定假人身体各部位与地面的摩擦系数为0.7，定义假人与地面的接触。调整假人的姿势，保证头部撞击点位于枕骨偏右侧。MADYMO软件的仿真过程见图3。由于事故描述中的跌落高度是在0.9～1.5 m之间，对假人的跌落高度进行调整。在保证撞击位置满足事故描述要求的前提下，将仿真1、仿真2和仿真3中假人的重心高度，分别设定为0.9、1.2、1.5 m，获得在此3种跌落高度下的儿童头部碰撞地面前瞬间的速度，具体数值如表6所示。

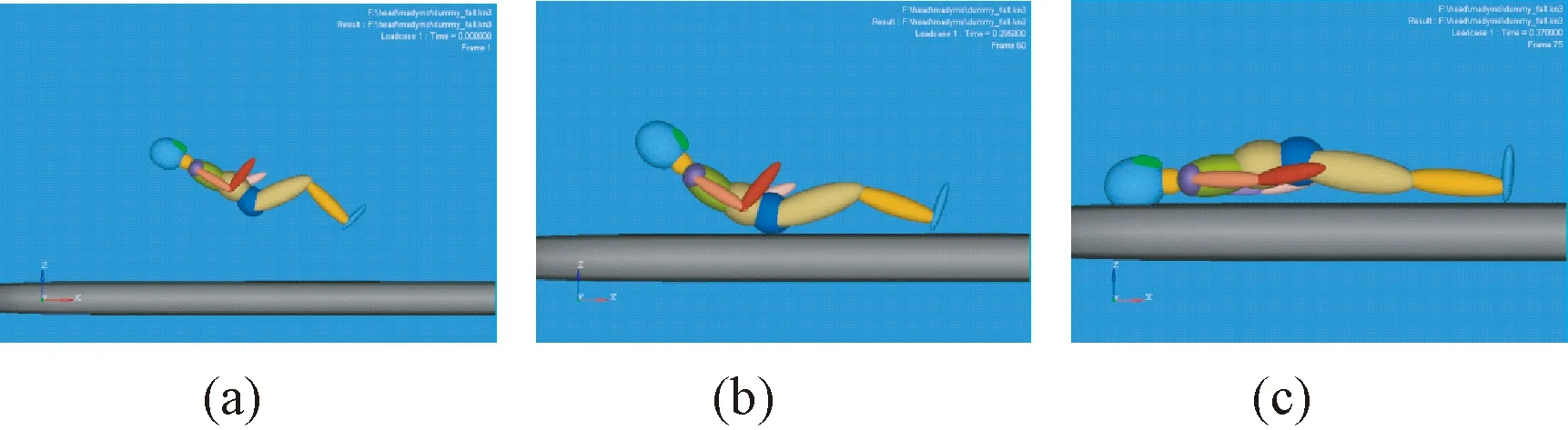
图3 事故儿童假人跌落过程。(a)假人刚开始跌落时刻；(b)假人身体接触地面时刻；(c)假人头部接触地面时刻Fig. 3 Falling process of the child. (a) Initial time of the fall;(b) Initial time of the contact between dummy body and ground; (c) Initial time of the contact between dummy head and ground

1.3.2基于事故重建的仿真设置

在HYPERMESH中建立地面网格，并根据MADYMO软件中头部与地面发生碰撞的位置和角度调整有限元模型，确保有限元模型与多刚体假人模型的头部具有完全相同的方位。由于头部与地面撞击的时间极短(6 ms)，因此忽略颈部对头部运动响应的影响，设定头部有限元模型为自由边界。3组仿真中，将受害者头部接触地面的速度设定为表6中对应的数值，确保运动的一致性。碰撞模型见图4。

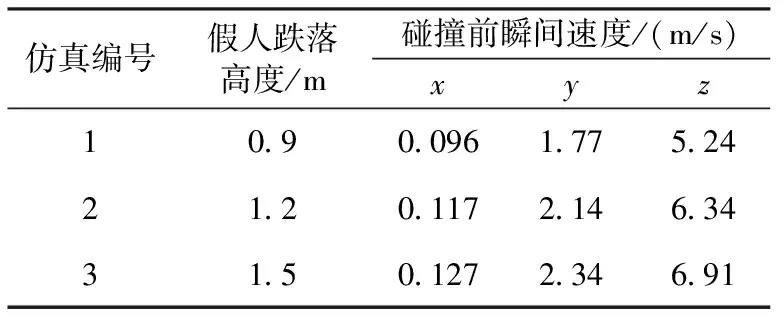
表6 事故重建结果

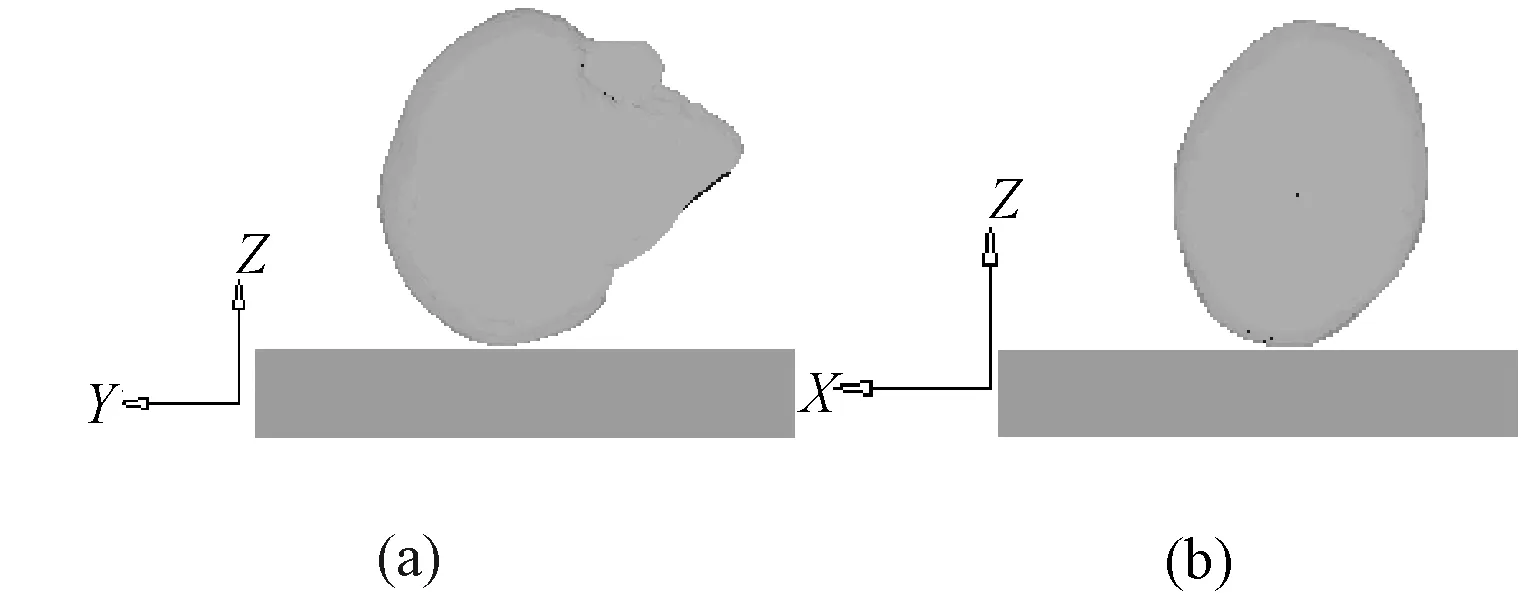
图4 头部跌落模型。(a)YZ 视图;(b)XZ视图Fig. 4 Loading model of the head. (a) YZ view; (b) XZ view

2 仿真损伤结果分析

2.1颅骨损伤分析

图5和图6分别为颅骨应力分布云图和颅骨应变分布云图。颅骨的最大应力和最大应变均出现在撞击点附近，且随着跌落高度的增加，同一部位的应力值和应变值均增大。如图5所示，3组仿真中预测到颅骨的最大von-mises应力为42.3 MPa，小于6岁儿童颅骨极限应力(Davis等[11])及成人颅骨极限应力(McElhaney等[16])。如图6所示，3组仿真中预测到颅骨的最大von-mises应变为0.89%，同样小于6岁儿童颅骨极限应变(Davis等，2012[11])及成人颅骨极限应变(McElhaney等[16])。从表7中可以看出，有限元模型预测在该事故中将不会发生颅骨骨折的损伤，这与事故描述的颅骨损伤情况一致。

2.2脑组织损伤分析

在碰撞过程中，头部的受力情况较为复杂。本研究在参考文献[19]的基础上，选用颅内压和von-mises应力作为判断脑组织损伤的物理参数，对事故中儿童脑部的损伤位置和严重程度进行预测。图7为颅内压力达到最大值时颅内压分布云图。

图5 颅骨von-mises应力分布云图。(a)仿真1；(b)仿真2；(c)仿真3Fig. 5 Von-mises stress contour of the skull. (a) Simulation 1; (b) Simulation 2; (c) Simulation 3

图6 颅骨von-mises应变分布云图。(a)仿真1；(b)仿真2；(c)仿真3Fig. 6 Von-mises strain contour of the skull. (a) Simulation 1; (b) Simulation 2; (c) Simulation 3

表7颅骨损伤分析

Tab.7FEsimulationresultofskulldamage

仿真编号123参考极限值颅骨应力/MPa31 933 042 36岁儿童颅骨极限应力：82 87[11] 成人颅骨极限应力：96 53[16]颅骨应变/%0 820 840 906岁儿童颅骨极限应变：3 3[11] 成人颅骨极限应变：5 1[16]

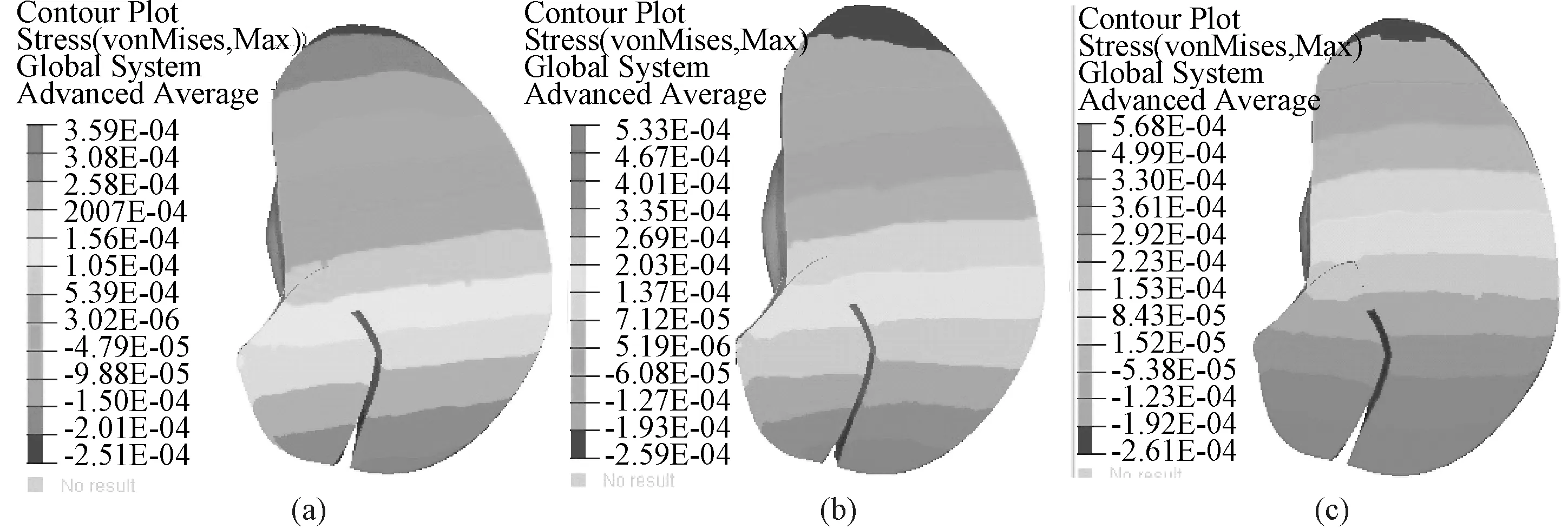
图7 脑组织压力分布云图。(a)仿真1；(b)仿真2；(c)仿真3Fig. 7 Pressure contour of the brain tissue. (a) Simulation 1; (b) Simulation 2; (c) Simulation 3

3组仿真中，撞击侧最大压力均分布在枕叶处，峰值分别为359、533、568 kPa；撞击对侧最大压力均分布在额叶处，峰值分别为-251、-259、-261 kPa。与文献[20]中提出的颅内压力耐受极限相比，3组仿真中撞击侧及撞击对侧的颅内压力均超过了参考极限值，表明儿童在此事故中将会遭受严重的脑组织损伤，与事故描述的脑组织损伤程度一致。

图8为脑组织von-mises应力达到最大值时脑组织应力分布云图。3组仿真中，脑组织的von-mises应力极值，均分布在额叶与右顶叶相交处和颞叶外侧，与受害者头部出现硬脑膜下血肿及颞叶沟回疝的位置高度吻合。该位置的von-mises应力在3组仿真中的响应情况较为一致，以3号仿真为例(见图9)，在碰撞接触后的4.8 ms时刻，von-mises应力达到最大值，其后出现回落。3组仿真中，脑组织的最大von-mises应力分别为4.02、5.19、7.08 kPa。与文献[21]中提出脑组织皮层von-mises应力耐受极值(7 kPa)相比，仅有当跌落高度为1.5 m的仿真3结果中，最大的von-mises应力超过了参考极限值；与文献[22]中提出的脑组织von-mises应力耐受极值(11～16.5 kPa)相比，3组仿真中脑组织最大von-mises应力均未超过参考极限值。

图8 脑组织von-mises应力分布云图。(a)1号仿真；(b)2号仿真；(c)3号仿真Fig. 8 Von-mises stress contour of the brain tissue. (a) Simulation 1; (b) Simulation 2; (c) Simulation 3

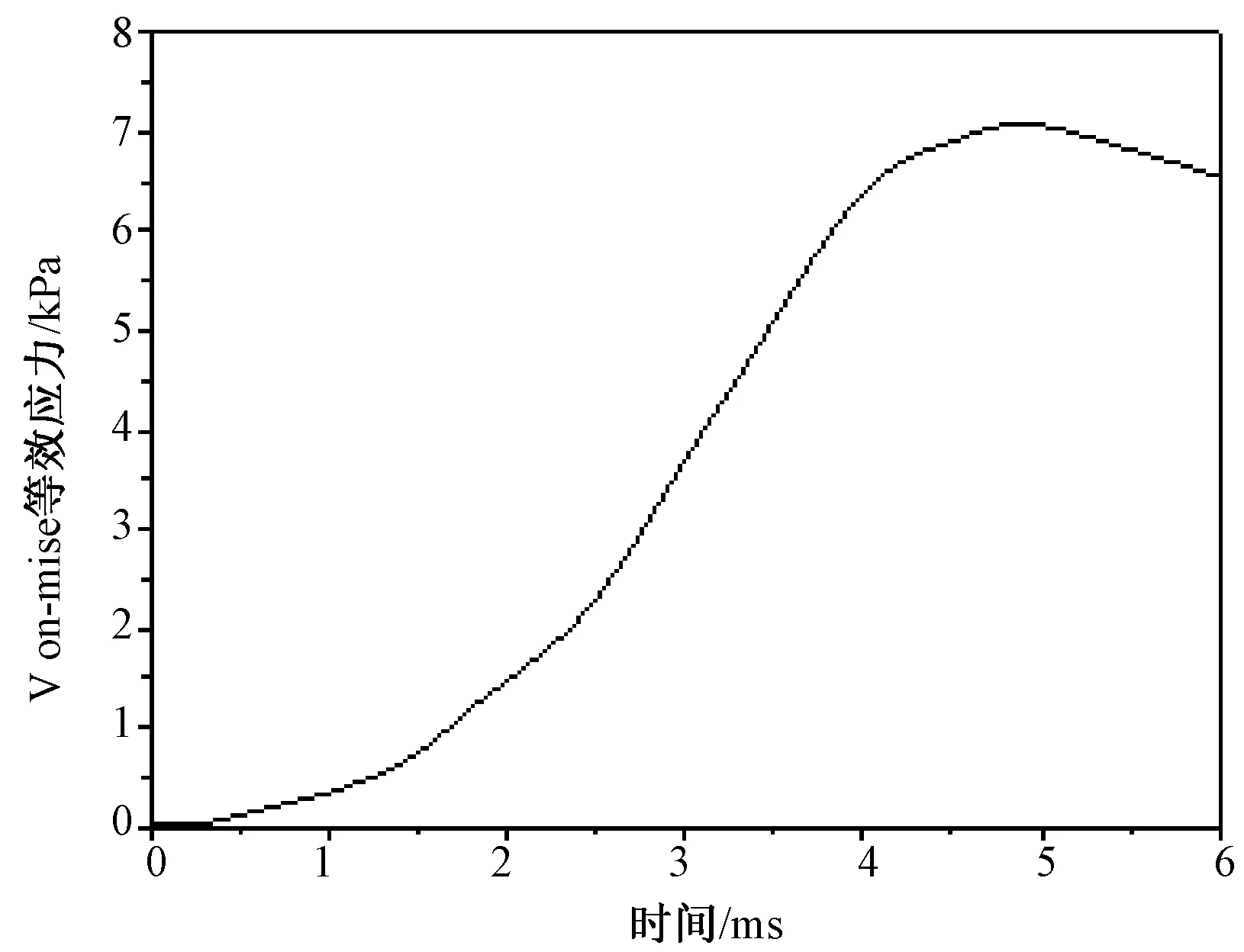
图9 仿真3 von-mises等效应力-时间曲线(额叶与顶叶交界处) Fig. 9 The curve of the von-mises stress in simulation 3 (The junction of the frontal and parietal lobes)

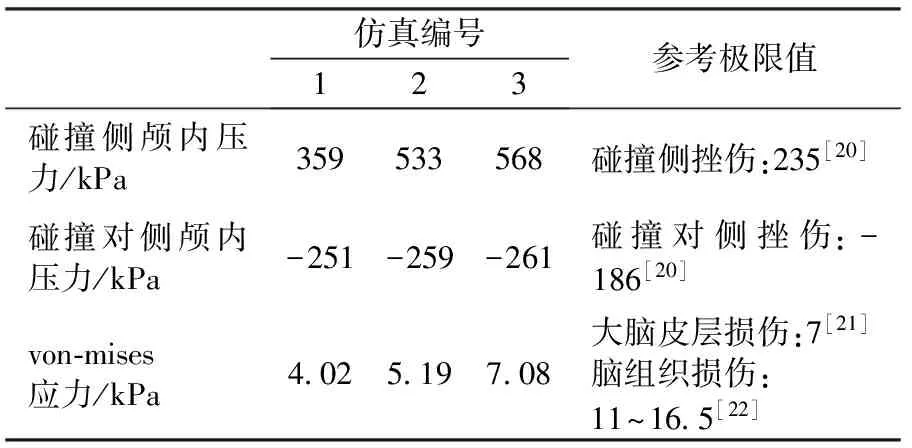
表8 脑组织损伤分析

3 讨论

脑组织损伤分析结果表明，采用颅内压力预测脑组织损伤时，出现最大正压的位置和最大负压的位置分别为枕叶和额叶，并在脑组织内形成了均匀的压力梯度，这与Ward等的实验和仿真结果[20]较为一致。基于颅内的最大正压和最大负压比较准确地判断出了脑组织的损伤程度，但无法预测事故中脑组织的损伤位置；而采用von-mises应力预测脑组织损伤时，则较为准确地判断出了受害人的损伤部位为额叶与右顶叶的交界处和右颞叶外侧。造成这一差异的主要原因，是由于颅内压和von-mises应力是不同载荷作用的结果。在跌落瞬间，坚实的地面对头部造成了巨大的冲击，使得撞击位置的颅骨产生一定的变形，而导致撞击处的局部脑损伤；与此同时，快速接触载荷会产生应力波，且当应力波在脑内传播时，致使颅内形成压力梯度而导致脑组织的局灶性损伤和擦伤。此外，接触载荷还可能导致大脑表面产生相对于颅骨内表面的运动，使得脑组织承受较大的应力，而造成大脑表面挫伤和桥静脉的撕裂(造成硬脑膜下血肿)。故该事故中出现在额叶与右顶叶交界处的硬脑膜下血肿和右颞叶外侧的脑疝，应是由大脑表面与颅骨内表面的相对运动造成的损伤，而不是接触位置的颅骨变形或颅内压力梯度所导致，因而难以依靠颅内压来判断损伤部位。但颅内压从侧面反映了头部受到的冲击载荷的大小及颅脑相对运动的严重程度。

此外，在利用von-mises应力预测脑组织的损伤程度时，与事故记录存在一定的差异。这主要是由于在缺乏儿童脑组织损伤极限数据的情况下，本研究选取的von-mises参考极限值，是研究者基于动物实验和成人实验的基础上得到的：如Miller等根据动物实验和模拟计算的结果，获得当von-mises应力超过7 kPa时，会对大脑造成严重损伤的结论[21]；而Kang等则是利用ULP成人头部模型与Hybrid假人连接，进行假人跌落仿真和重构摩托车交通事故，获得成人脑组织所能承受的von-mises极限应力在11～16.5 kPa之间[22]。因此，利用动物及成人脑组织von-mises应力耐受值来判断儿童脑组织的损伤严重程度时，可能会存在一定误差，还需进一步的研究，来获得更精确的10 岁儿童脑组织von-mises应力耐受限度。此外，所建立的头部模型中，脑组织与颅骨内表面采用共节点的连接方式，该模拟方法也可能导致模型预测到的脑组织von-mises应力偏低[23]。

4 结论

本研究以CT数据为依据，建立了一个10 岁儿童头部有限元模型。模型真实地反映了10 岁儿童头部解剖学结构及几何尺寸等特征。采用典型跌落事故重建的方法对所建模型进行了验证。3组仿真中，颅骨的最大应力和最大应变的分布位置与撞击点的位置高度吻合，但均未超过颅骨的耐受值；利用颅内压力及von-mises应力对脑组织的损伤情况进行了预测，并对基于不同损伤准则预测的脑组织损伤结果的差异进行了分析。模型的仿真结果与受害者损伤情况对比表明，本研究建立的10 岁儿童头部有限元模型具有足够的生物逼真度，基本能够预测颅骨及脑组织的损伤位置及损伤程度。

[1] 全球儿童安全网络(中国).儿童道路交通伤害状况[R/OL]． http://safekidschina.org. 2007-11-27/2013-4-22.

[2] 张良，周继红，李国林，等. 2000-2006年重庆地区0～19岁人群道路交通伤害特点与趋势[J]. 创伤外科杂志, 2011,13(3): 212-215

[3] 蒋彬辉.儿童胸部损伤机理[D].长沙:湖南大学, 2013.

[4] Roth S, Vappou J, Raul JS,etal. Child head injury criteria investigation through numerical simulation of real world trauma[J]. Computer Methods and Programs in Biomedicine, 2009,93(1): 32-45.

[5] Nahum AM, Smith R, Ward C. Intracranial pressure dynamics during head impact[C]//Proceedings of the 21stStapp Car Crash Conference. Warrendale: SAE International Society of Automotive Engineers, 1977:339-366.

[6] 阮世捷，李盼东，李海岩，等. 6岁儿童头部有限元模型的构建与验证[J].中国生物医学工程学报, 2012,31(4):502-506.

[7] 曹立波，高海涛，冒浩杰. 三岁儿童头部有限元模型的建立及验证[J]. 汽车工程, 2013,35(1): 56-59.

[8] Dekaban AS. Tables of cranial and orbital measurements, cranial volume, and derived indexes in males and females from 7 days to 20 years of age[J]. Annals of Neurology, 1977,2(6): 485-491.

[9] Wittek A, Omori K. Parametric study of effects of brain-skull boundary conditions and brain material properties on responses of simplified finite element brain model under angular acceleration impulse in sagittal plane[J]. JSME International Journal Series C, 2003,46(4): 1388-1399.

[10] Motherway JA, Verschueren P, Van der Perre G,etal. The mechanical properties of cranial bone: the effect of loading rate and cranial sampling position[J]. Journal of Biomechanics, 2009,42(13): 2129-2135.

[11] Davis MT, Loyd AM, Shen HH,etal. The mechanical and morphological properties of 6 year-old cranial bone[J]. Journal of Biomechanics, 2012,45(15):2493-2498.

[12] Prange MT, Luck JF, Dibb A,etal. Mechanical properties and anthropometry of the human infant head[J]. Stapp Car Crash Journal, 2004,48:279-299.

[13] Margulies SS, Thibault KL. Infant skull and suture properties: Measurements and implications for mechanisms of pediatric brain injury [J]. Journal of Biomechanical Engineering, 2000,122(4): 364-371.

[14] Weber W. Biomechanical fragility of the infant skull[J]. Journal of Legal Medicine, 1985,94(2): 87-94.

[15] McPherson GK, Kriewall TJ. The elastic modulus of fetal cranial bone: a first step towards an understanding of the biomechanics of fetal head molding[J]. Journal of Biomechanics, 1980,13(1): 9-16.

[16] McElhaney JH, Fogle JL, Melvin JW,etal. Mechanical properties of cranial bone[J]. Journal of Biomechanics, 1970,3(5): 495-511.

[17] Yang KH, Hu J, White NA,etal. Development of numerical models for injury biomechanics research: a review of 50 years of publications in the Stapp Car Crash Conference[J]. Stapp Car Crash Journal, 2006,50: 429-490.

[18] Plunkett J. Fatal pediatric head injuries caused by short-distance falls[J]. The American Journal of Forensic Medicine and Pathology, 2001,22(1): 1-12.

[19] Yang JK. Review of injury biomechanics in car-pedestrian collisions[J]. International Journal of Vehicle Safety, 2005,1(1) : 100-117.

[20] Ward CC, Chan M, Nahum AM. Intracranial pressure—a brain injury criterion[C]// Proceeding of the 24thStapp Car Crash Conferences. Troy: Society of Automotive Engineers, 1980:347-360.

[21] Miller RT, Margulies SS, Leoni M,etal. Finite element modeling approaches for predicting injury in an experimental model of severe diffuse axonal injury[J]. SAE Transactions, 1998,107(6): 2798-2810.

[22] Kang HS, Willinger R, Diaw BM,etal. Validation of a 3D anatomic human head model and replication of head impact in motorcycle accident by finite element modeling[C]//Proceedings of Stapp Car Crash Conference. Florida: Society of Automotive Engineers SAE, 1997: 329-338.

[23] Aomura S, Fujiwara S, Ikoma T. Study on the influence of different interface conditions on the response of finite element human head models under occipital impact loading[J]. JSME International Journal Series C, 2003,46(2): 583-593.

DevelopmentandValidationoftheFEModelfora10-Year-OldChildHead

CAO Li-Bo ZHOU Zhou JIANG Bin-Hui*ZHANG Guan-Jun

In this study, the software ANSYS ICEM CFD and HYPERMESH was used to develop a finite element (FE) model for 10-year-old child head with detailed anatomical characteristics. The MADYMO models of crash dummies were used to simulate the dynamic responses of an injured child in a typical falling accident from three different heights, and the motion parameters of orientation and velocity of the child head at the moment of impact were calculated. These parameters were input into the 10-year-old child head finite element model to simulate the head response during the fall impact and analyze the injury-related biomechanics parameters. Results showed that the location of maximum von-mises stress and maximum von-mises strain in the skull matched well with the impact site located on the right side of the occipital, but within their limits of tolerance. The intracranial pressure could accurately predict the injury level, while the von-mises stress could approximately recognize the traumatic location. The accident reconstruction results indicate that the constructed model has a good biofidelity and can be used for the further study of the child head injury mechanism.

head injury; finite element model; accident reconstruction; 10-year-old child

10.3969/j.issn.0258-8021. 2014. 01.010

2013-08-20，录用日期：2013-12-23

国家自然科学基金(11172099)

R318

A

0258-8021(2014) 01-0063-08

*通信作者。E-mail: jjhhzz123@126.com