DICE/RICE模型中碳循环模块的比较

吴 静，朱潜挺，刘昌新，王 铮,3,*

(1. 中国科学院科技政策与管理科学研究所，北京 100190; 2. 中国石油大学(北京)工商管理学院，北京 102249;3. 华东师范大学地理信息科学教育部重点实验室， 上海 200062)

DICE/RICE模型中碳循环模块的比较

吴 静1，朱潜挺2，刘昌新1，王 铮1,3,*

(1. 中国科学院科技政策与管理科学研究所，北京 100190; 2. 中国石油大学(北京)工商管理学院，北京 102249;3. 华东师范大学地理信息科学教育部重点实验室， 上海 200062)

碳循环模型的正确构建是影响综合集成评估模型IAM(Integrated Assessment Model)模拟结果的重要因素之一。DICE/RICE模型中的碳循环模型主要有两个，即Nordhaus单层碳库模型和Nordhaus三层碳库模型，但这两个模型的主要缺陷是不考虑陆地生态系统在碳循环中的贡献，因此，引入了包含陆地生态系统的Svirezhev碳循环模型，并将其与Nordhaus单层碳库模型、Nordhaus三层碳库模型展开比较研究。结果表明，在基于历史数据的模型检验中，Svirezhev碳循环模型对全球二氧化碳浓度模拟的准确度优于其他两个模型。对于未来全球气候变化的模拟，3个模型模拟得到了至2100年的温度预测值分别为2.98,3.54,2.91℃，二氧化碳浓度值分别为608.04,733.04,594.70μL/L。 其中，Svirezhev碳循环模型的模拟值在3个模型中最低，表明了陆地生态系统和海洋对二氧化碳的吸收作用对抑制全球升温的贡献；而分析也发现Nordhaus三层碳库模型对陆地生态系统和海洋碳库的模拟与实际观测值偏离较大。最后，通过敏感性分析，研究发现DICE/RICE模型中使用的气候响应模块在短期温度模拟中对地表温度的初值较为敏感，在长期温度模拟中敏感度显著下降。总之，从碳循环机制的模拟性能而言，Svirezhev碳循环模型优于其他两个模型，而Nordhaus单层碳库模型虽然机制较为简单却保证了模拟的准确性，但Nordhaus三层碳库模型虽然丰富了碳库的表征，实际上各碳库的模拟准确性差，降低了模型的可靠性。

IAM；碳循环；陆地生态系统；碳库; 全球气候和经济动态模型(DICE); 区域气候和经济动态模型(RICE)

自1970年代以来，针对全球气候变化政策模拟的综合集成评估模型(Integrated Assessment Model, IAM)得到了广泛的发展。所谓IAM，是整合气候变化的科学性、社会-经济性等各方面要素的建模方法，它以评价气候变化控制政策选择为主要目的[1]。Nordhaus认为全球气候保护IAM的框架有5个基本组成部分，即包括碳排放、碳循环、气候系统、影响评估、政策措施[2]。其中，碳循环模块主要模拟了人类活动引起的碳排放在大气-海洋-生物圈碳库之间的转移、吸收的过程，碳循环引起的大气碳含量直接影响着大气辐射强迫的变化，从而作用于模型对全球升温的估算和预测。Van Vuuren 等人[3]，Warren等人[4]认为IAM对碳循环和气候响应模式的不同表征将引起模型结果的显著差异。实际上，在IAM中，碳循环模拟不仅实现了大气碳平衡变化的模拟，同时它所涉及的地理过程为气候适应和减排提供了可操作的政策接口，包括增汇、土地利用类型变化等。因此，正确建模对IAM的升温预测以及减排政策制定具有重大的影响意义。

从理论上说，大气环流模型(General Circulation Model,GCM)是气候保护建模中碳循环建模的最理想方法。但是由于GCM模型细节过于繁杂、规模宏大，动辄涉及成千上万的方程，故不能很好地融合到IAM中来，特别是很难与具有实时决策支持功能的IAM相结合。因此，在IAM中普遍采用的做法是在保证全球碳循环特征的前提下，抽象出较简单的地球物理系统模型，再与气候保护的建模相结合。通常IAM中的碳循环模型为整体模型或零维模型，这类模型将全球看作一个整体，计算全球地表平均温度[5- 8]。

当前，在诸多IAM模型中，DICE/RICE模型是发展较早且得到广泛应用模型之一。1992年，Nordhaus正式提出了一个针对全球气候变化政策模拟的DICE(Dynamic Integrated model of Climate and the Economy)模型[9- 10]，并于1996年发展为多区域的RICE(Regional dynamic Integrated model of Climate and the Economy)模型[6]。虽然国内外学者已经对DICE/RICE模型展开了大量的扩展和改进工作，包括对内生技术进步的改进[11- 14]；对GDP溢出的扩展[15]；等等。但这些工作大多都集中在经济系统的建模，对于DICE/RICE模型的碳循环的改进却非常少。相对于早期DICE/RICE模型中碳循环的建模，即二氧化碳只存在于大气中并以一个恒定的速率从大气中衰减[16- 17]，唯一对于DICE/RICE模型碳循环机制的改进是1999版的DICE/RICE模型将早期的碳循环模型发展为三层碳库的碳循环模型，即二氧化碳在大气、上层生物圈/浅层海洋、深层海洋之间循环。那么，改进之后的碳循环模块的模拟性能是否有所提高，又是否存在不足之处，这在以往的研究中并未得到论证。

因此，本文将比较DICE/RICE模型的单层碳库模型和三层碳库模型，并引入Svirezhev碳循环模型与前两者模型进行比较，以此分析各个模型在IAM碳循环建模中的优劣所在。为DICE/RICE模型或IAM模型找到一个较优的碳循环模拟模型。

1 模型

1.1 DICE/RICE模型中的碳循环及气候响应建模

早期的DICE/RICE模型中，只存在一个大气碳库，大气中碳含量随时间的变化为[16]：

M(t)-590=βiE(t-1)+(1-δm)(M(t- 1)-590)

(1)

式中,M(t)是t阶段的大气碳含量(GtC)，βi表示二氧化碳在大气中的停滞率。一单位的值βi意味着每吨排放出来的二氧化碳变为了一吨大气中存在的二氧化碳。E(t-1)为前一期的碳排放量(GtC)，参数δm为衰减率，它假设在前工业化时期590GtC的水平上，大气中的二氧化碳是慢慢衰减的，即逐渐被海洋等吸收[16]。为表述方便，下文将基于(1)式的模型称为“Nordhaus单层碳库模块”。

1999年，在DICE/RICE99中，Nordhaus[17]将碳循环改进为三层碳库模型，即大气碳库MAT(GtC)、上层海洋与生物圈碳库MUP(GtC)、深层海洋碳库MLO(GtC)，相邻两碳库间存在碳传递，用方程表示为[17]：

(2)

MUP(t)=φ12MAT(t-1)+φ22MUP(t-1)+φ32MLO(t-1)

(3)

MLO(t)=φ23MUP(t-1)+φ33MLO(t-1)

(4)

式中，φij表示了碳库间的碳传递系数。为表述方便，下文将基于(2)—(4)式的模型称为“Nordhaus三层碳库模块”。

而DICE/RICE模型中气候响应模块的建模在改进前后并未发生变化。在基于(1)式、(2)式描述的大气碳含量的变化下，全球辐射强迫水平F(t)变化满足：

(5)

其中，MAT(1750)为1750年工业化以前的大气碳含量；由于DICE/RICE模型主要是评估二氧化碳对全球气候变化的影响，而未纳入其他温室气体如甲烷、氧化亚氮等的影响作用，故将其他温室气体导致的辐射强迫变化在(5)式中以FEX(t)予以考虑(W)，FEX(t)满足：

(6)

增加的辐射强迫最终导致全球温度的上升：

TAT(t)=TAT(t-1)+ξ1{F(t)-ξ2TAT(t-1)-ξ3[TAT(t-1)-TLO(t-1)]}

(7)

TLO(t)=TLO(t-1)+ξ4{TAT(t-1)-TLO(t-1)}

(8)

式中，TAT(t)为地表温度(℃)，TLO(t)为深海温度(℃)。分析以上两个模型的优劣所在，可以发现：Nordhaus单层碳库模型只考虑了碳在大气中的滞留和衰减，模型未能对碳循环的基本循环过程进行建模，从建模机制上说单层碳库模型显得过于简单。

Nordhaus三层碳库模型则对碳循环的过程区分了大气、上层海洋/生物圈、深层海洋3个主要的碳库，这符合通常认识的碳循环过程。但是深究其内部结构，发现了Nordhaus三层碳库模型所存在的不足之处：①各碳库之间的传递系数为常数，这样就忽略了温度变化对不同碳库吸收率的影响[18]，也忽略了各碳库的当前碳含量水平对下阶段碳溶解率的影响；②将陆地生态系统与海洋表层作为一个整体碳库考虑，这样就不能对在全球碳循环产生重要影响作用的陆地生态系统的固碳能力展开进一步的模拟研究， Fang,等人[19]，方精云等人[20]研究表明北半球中高纬度陆地生态系统在全球碳循环中起着重要的碳汇作用，其值可达2—3PgC/a，同时Liu, 等人[21]研究表明全球森林固碳潜力巨大，因此，在IAM中不能对陆地生态系统的碳汇作用简单处理，而需要进一步的细化模拟。

1.2 Svirezhev碳循环及气候响应建模

针对DICE/RICE模型中碳循环模型的不足，本文引入Svirezhev 等人提出的一个以大气、陆地生态系统、海洋碳库为主体的三层零维模型[22]。与GCM相比，该模型也只是一个简化的碳循环模型，但也正是由于其简化性使其能很好地与IAM建模相整合实现对全球碳循环过程的模拟。为表述方便，下文将Svirezhev等人[22]提出的碳循环模型简称为“Svirezhev碳循环模块”，其模型详细结构如下：

(1)陆地生态系统碳循环

陆地生态系统碳循环由两部分组成，即生物碳和土壤碳。定义N(t)为陆地植被中的碳(GtC)，则：

(9)

式中，P(C,N,T)是植被的年净初级生产力，单位为GtC/a；m(t)为植被中碳逃逸率。但由于Leith认为NPP只与生态条件相关(如温度、降水)[22]，因此P(C,N,T)进一步被具体表示为：

P(C,T)=P0(1+a1T)(1+a2(C-C0))

(10)

式中，P0为工业化以前的净初级生产力。

另外，(9)式中m(t)满足：

(11)

式中，τB(t)为碳在植被中滞留的时间，也就是说植被碳的逃逸率与其滞留时间成反比。从植被中逃逸出来的碳又分为长期存留和短期存留两种类型，前者将转化为土壤碳，后者将以二氧化碳的形式被释放出来进入大气中。这里以ε表示长期存留碳占生物质碳逸出总量的比例，则短期存留碳所占比例为1-ε。因此，得到土壤碳含量S(t)的传递量为：

(12)

式中，δ(T)为土壤碳分解率。(12)式表明土壤碳的变化量除了吸收来自植被释放的碳，自身也通过分解过程释放部分碳。土壤碳分解率受当期的温度影响定义为(13)式：

δ(T)=δ0(1+a3T)

(13)

可以看出随温度的升高，土壤碳的分解率也将增加，也就将有更多的碳从土壤中逃逸出来到大气中去。

(2)海洋碳循环

每一期，海洋碳含量变化不仅受到海洋上一期碳含量水平的影响，同时还受到大气碳含量水平的影响，即部分大气中的碳将融入海洋，得到海洋碳的传递量为：

(14)

其中，σ,ξ为相关参数。

(3)大气碳循环

在陆地碳循环、海洋碳循环作用下，大气碳循环的碳传递量为：

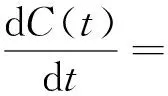
(15)

式中，E(t)为人类活动产生的碳排放。

(4)气候子系统

在气候响应模块，与DICE/RICE模型不同，Svirezhev等人定义的气候响应模型较为简单。全球地表温度T(t)满足：

(16)

式中，C(t)为大气碳含量，C0为工业化以前的大气碳含量，μ和α为模型参数。

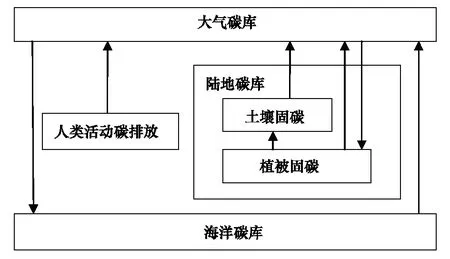
图1 Svirezhev碳循环模型结构图Fig.1 The structure of Svirezhev carbon cycle model

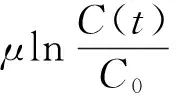
为了弥补Svirezhev碳循环模块中气候响应模块的不足，同时也为了避免由于气候响应模块不同而引起的全球升温趋势模拟差异。本文将DICE/RICE模型中的气候响应模块链接到Svirezhev碳循环模块上，即用(5)—(8)式代替(16)式的气候响应模块。从而构造了3个可以比较不同碳循环机制影响差异的碳循环-气候响应模型，如图2所示，下文将分别简称该3个模型为N1-N模型、N3-N模型、S-N模型。在3个模型下，碳循环模块的大气碳含量输出作为气候响应模块的输入，气候响应模块基于该输入获得全球的温度变化，碳循环模块与气候响应模块均处于松耦合状态。

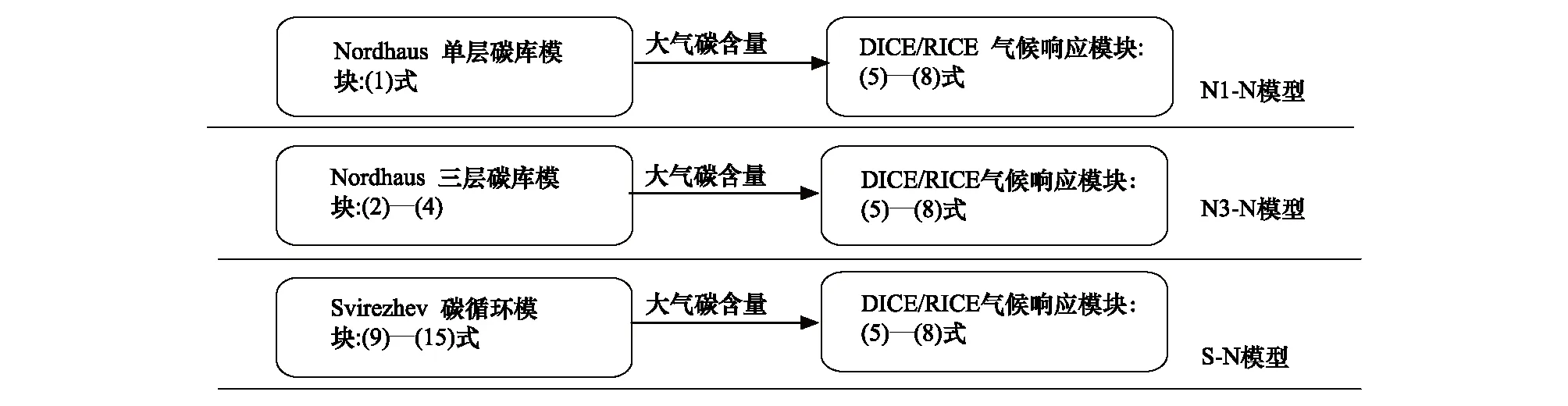
图2 3个碳循环-气候响应模型示意图Fig.2 Comparison of the three carbon cycle-climate response models

2 参数取值和计算实现

由于篇幅有限，这里不能一一罗列各模型的参数取值，对于Nordhaus单层碳库模块及其响应的气候响应模块的参数，读者可参考Pizer[16]，王铮等人[23]，Nordhaus，Yang[6]，Nordhaus, Boyer[17]；对于Svirezhev碳循环模块可参考Svirezhev等人[22]。但需要特别处理的是，对于Nordhaus三层碳库模块来说，由于Nordhaus, Boyer[17]原模型的时间间隔为10a，因此碳库的传递系数也为每10a各碳库碳传递的系数值(表1)，其中各列的加和等于1，即保证了各碳库在传递中的总量守恒。但由于各碳库间碳传递的非线性，不能简单将10a的传递系数作用于1a的碳传递方程中。因此，将(2)，(3)，(4)式中各碳库系数矩阵的转移矩阵作为每年的传递系数矩阵(表2)，从而保证了每10a各碳库间的碳传递总量与Nordhaus, Boyer[17]原模型一致，且保证了3个碳库间的年传递量守恒。

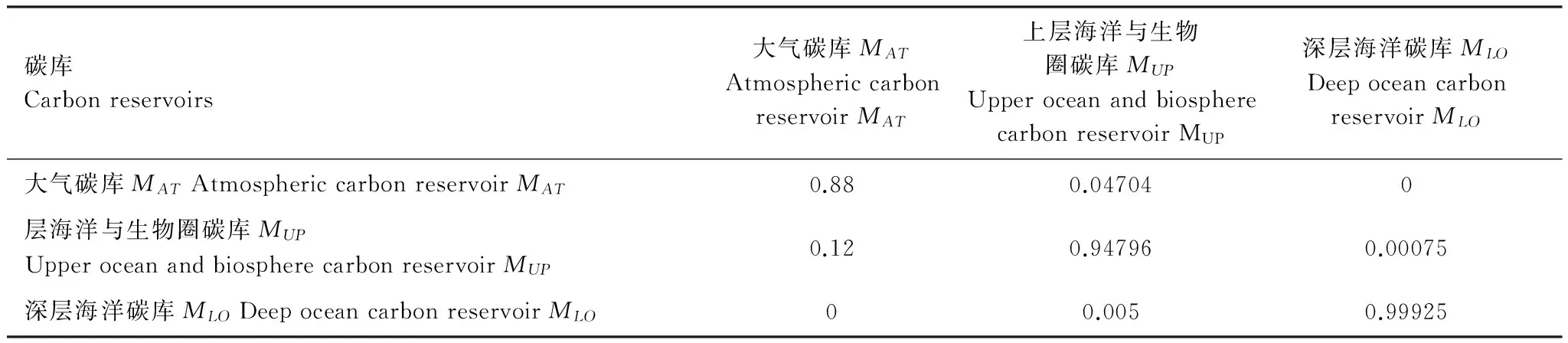
表1 Nordhaus三层碳库模块的10a碳传递率矩阵[24]

在计算实现上，采用Visual C#为开发工具分别对以上3个模型单独进行编程实现，而将人类活动引起的碳排放数据作为各个模型的输入数据，也就是说3个模型具有完全一致的输入，就可以从输出结果的差别上分析模型的性能差别。

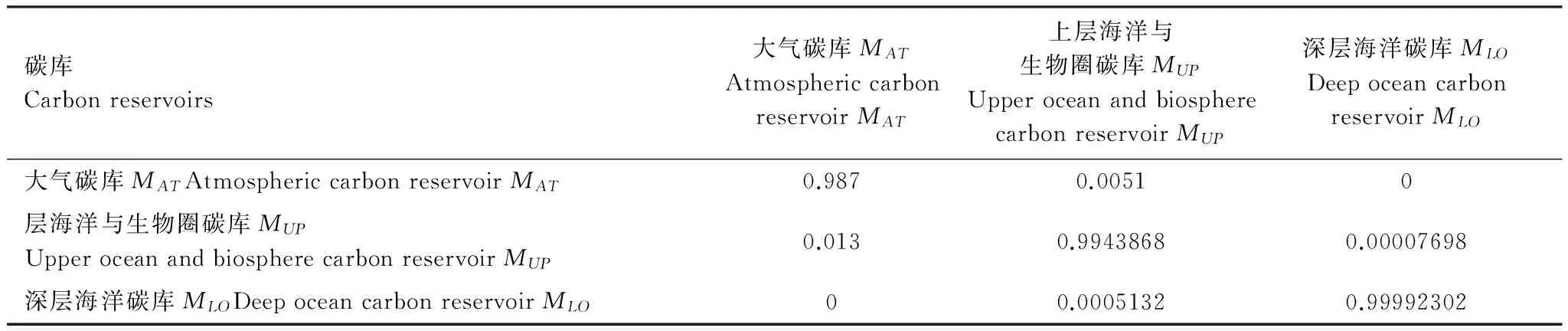
表2 Nordhaus三层碳库模块的1a碳传递系数矩阵

3 模拟结果分析

3.1 模型检验

上文介绍的3个碳循环-气候响应模型对未来全球升温和全球二氧化碳浓度模拟的性能究竟如何？首先对3个模型的准确性进行了检验。本文以2001—2008年的全球历史碳排放数据作为检验的输入数据。这里之所以选取2001—2008年作为检验数据的起讫年原因在于：①Nordhaus三层碳库模块的参数基准年为2000年，虽然另外两个模型的基准年为1995年，但为了保持3个模型基准年的一致性，将另外两个模型的基准年也校准到2000年；②由于数据的可获得性限制，目前能获得的权威的全球碳排放数据仍只截止到2008年。

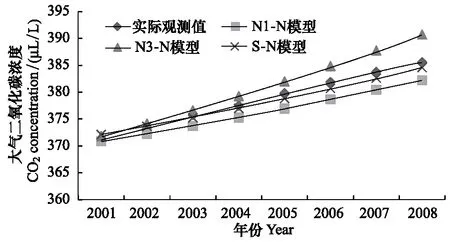
图3 2001—2008年全球二氧化碳浓度模拟值与实际观测值比较Fig.3 Comparison of simulated and realistic CO2 concentration in 2001—2008

模拟得到，3个模型下全球二氧化碳浓度的变化如图3所示。可以发现，N3-N模型的大气二氧化碳浓度略高于实际观测值，该模型模拟值与实际观测值的相关系数为0.99，方差为0.45；而N1-N模型和S-N模型的模拟值稍低于观测值，这两个模型与实际观测值的相关系数分别为0.99,0.99，方差分别为0.34,0.84。因此，整体上说，3个模型对于全球大气二氧化碳浓度的变化趋势模拟均获得了较好的结果，模拟值与实际观测值没有显著差异，两者高度相关。为了进一步比较模拟的准确度，计算得到N1-N模型、N3-N模型和S-N模型下的RMSE(均方根误差，也称标准误差)分别为2.53,2.76,0.89，分别占2001—2008年二氧化碳浓度实际观测值的0.67%，0.73%，0.23%，结果显示了S-N模型的标准误差显著小于其他两个模型。由于对于二氧化碳浓度的模拟是由碳循环模块完成的(图2)，因此，结果也揭示了Svirezhev碳循环模块对历史二氧化碳浓度的模拟的准确度显著优于其他两个模型。

当碳循环模块模拟得到的大气碳含量被输入到气候响应模块，这样就模拟得到3个模型下全球2001—2008年的升温趋势如图4所示。可以发现，实际观测值温度呈显著的锯齿型波动，而模拟值均为单调的线性上升趋势，这主要是由于实际的全球升温过程不仅受到人类碳排放的影响，还受到很多其他自然因素的干扰，是多种要素对温度影响的叠加效果，但本文只考虑了人类活动引起的碳排放对温度的驱动作用。进一步分析，3个模型对全球升温的模拟值均低于全球实际的观测值，但3个模型模拟值间的差别十分微小，升温模拟轨迹几乎重叠。计算得到，N1-N模型、N3-N模型和S-N模型的模拟值与实际观测值的相关系数分别为0.45,0.45,0.45，方差分别为0.003,0.006,0.004，RMSE分别为0.18,0.18,0.18，分别占2001—2008年实际平均温度的19.5%,18.7%,19.1%。可以判断，在以2001—2008年为模型检验期时，3个模型的温度模拟值与实际观测值的相关系数均小于相应的相关系数临界值，模拟值与观测值相关性较差，两者存在显著差异，表明模拟值不能很好地反映实际温度的变化趋势；同时，3个模型的标准误差也较大，反映了模型对于温度模拟的准确性也仍有待提高。

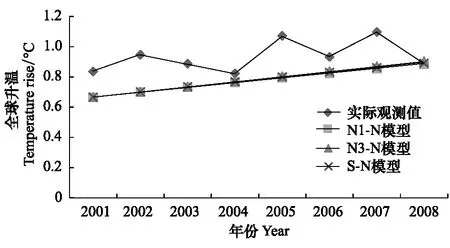
图4 2001—2008年全球升温模拟值与实际观测值比较Fig.4 Comparison of simulated and realistic temperature rise in 2001—2008

由于3个模型对全球二氧化碳浓度变化的模拟在趋势性和准确性上都获得了比较好的结果，与实际值高度相关；但高相关性的大气二氧化碳模拟结果却最终得到了低相关性的温度模拟结果，3个模型对全球温度变化的模拟均不理想。考虑碳循环模块与气候响应模块之间的松耦合性，可以判断3个模型对温度模拟的失败，主要问题出在气候响应模块，需要进一步的探讨。

考虑到上文对模型检验所采用的数据起讫时间为2001—2008年，是一个比较短的时间序列，有可能会对气候响应模块的模拟准确性产生一定的影响。因此，试图将3个模型的检验基准年前推至1995年，但由于Nordhaus三层模型中Mup和Mlo参数的1995年取值的不可获得性，最终只能将N1-N模型和S-N模型的检验期扩展到1995—2008年。但这并不影响对气候响应模块的检验。模拟得到两个模型下全球1996—2008年的二氧化碳排放与升温趋势分别如图5、图6所示。其中，N1-N模型和S-N模型的二氧化碳模拟值与实际观测值的相关系数分别为0.99和0.99，方差分别为0.34和0.31，RMSE分别为4.03和2.91，分别占1996—2008年二氧化碳浓度实际观测值的1.07%，0.77%；同时，N1-N模型和S-N模型的温度模拟值与实际观测值的相关系数分别为0.71, 0.71,方差分别为0.18和0.37RMSE分别为0.16, 0.16，分别占1996—2008年平均温度的19.35%，19.44%。可以看出，当时间序列起点年前推至1995年，两个模型的碳循环模块对全球二氧化碳浓度的模拟仍保持了高度的相关性和准确性；而气候响应模块对全球温度的模拟较2001—2008年序列下的结果的相关性有所提高，模拟值较好地反映了温度的实际变化趋势，但模拟结果的准确性却仍较低。

图5 1996—2008年全球二氧化碳浓度模拟值与实际观测值比较Fig.5 Comparison of simulated and realistic CO2 concentration in 1996—2008

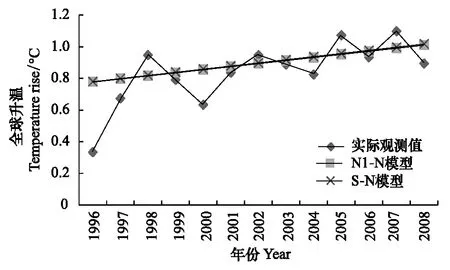
图6 1996—2008年全球升温模拟值与实际观测值比较Fig.6 Comparison of simulated and realistic temperature rise in 1996—2008

综上，3个碳循环模块能较好地模拟全球二氧化碳浓度变化，不仅获得了与实际观测值高度相似的模拟值，同时其准确度也较高；但3个模型共同采用的气候响应模块，即DICE/RICE气候响应模块，其模拟能力值得商榷，当检验的时间序列得到扩展时，模块对温度变化趋势性的模拟有显著提高，但准确性仍较低。

3.2 气候响应模块的敏感性分析

在模型检验中，当检验基准年由2000年前推至1995年时，模拟的相关性得到了显著的提高。其中除了时间序列延长对结果的影响之外，基于气候响应模块的建模方程，可以知道，基准年地表温度TAT，深海温度TLO的初值也是影响气候响应模块结果的主要因素。在分别以1995年和2000为基准年时，地表温度TAT，深海温度TLO的取值分别如表3所示。为了评估由于模型参数初始值取值不同引起的敏感度，基于对二氧化碳浓度模拟具有最优效果的Svirezhev碳循环模块(即S-N模型)，以2001—2008年全球历史排放为输入数据，展开了情景对比分析，情景假设如表4所示。

表3 不同基准年下的参数初始值

表4 短时间序列敏感性分析情景假设

Table 4 Scenario assumptions for the short-term sensitivity analyses

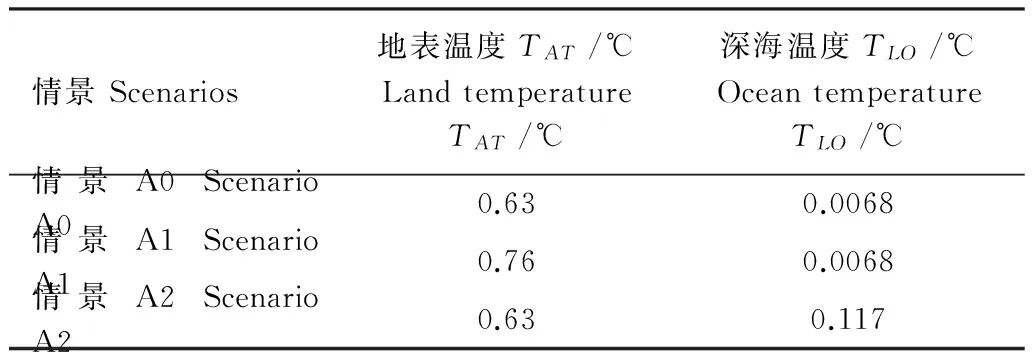
情景Scenarios地表温度TAT/℃LandtemperatureTAT/℃深海温度TLO/℃OceantemperatureTLO/℃情景A0ScenarioA00.630.0068情景A1ScenarioA10.760.0068情景A2ScenarioA20.630.117

模拟得到，情景A1、情景A2与情景A0的温度变化的比较如图7所示。观察发现，情景A1的模拟值比情景A0显著上升，而情景A2的模拟值与情景A0的差异十分微小。以各情景下2001—2008年的温度均值作为各情景的考察对象，情景A0，情景A1，情景A2下的温度平均值分别为0.78,0.86,0.79℃，则计算得到以情景A0为基准，由情景A1和情景A2下参数初始值调整而引起的结果敏感度分别为0.54和0.0007。这表明，在较短的时间序列上，DICE/RICE模型的气候响应模型对于地表温度初始值较为敏感，而对于深海温度初始值不敏感。

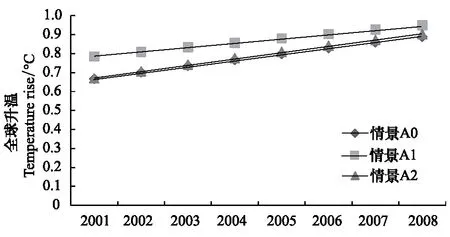
图7 气候响应模块短时间序列敏感度分析的升温比较Fig.7 Comparison of temperature rise in the short-term sensitivity analyses

那么进一步，该气候模型在长期时间序列上是否也对地表温度初始值表现出敏感性呢？为了保持分析的一致性，仍在S-N模型下，以王铮等人[26]开发的MRICES模型的基准情景下2005—2100年的全球碳排放量数据作为输入，针对气候响应模块取不同初始值的情景做了比较分析，具体情景假设见表5。模拟得到，3个情景下全球升温如图8所示，可以看到在模拟初期，情景B1的温度显著高于情景B0和情景B2。随着时间的变化，情景间的差别逐渐缩小，升温模拟值逐渐趋于一致，至2100年，3个情景下温度模拟值分别为2.919℃，2.919℃，2.923℃，方差仅为0.00002，可以认为不同初值下的温度预测值出现收敛。同样以各情景的温度平均值作为考察对象，情景B0，情景B1，情景B2下的平均温度分别为1.911℃，1.919℃，1.915℃，故计算得到情景B1和情景B2下参数初始值调整而引起的结果敏感度分别为0.04和0.02。相对于短时间序列的敏感度而言，地表温度初值的敏感度下降，深海温度初值的敏感度上升，但总体而言，长时间序列下气候模型对地表温度和海洋温度的敏感性均较小。

表5 长时间序列敏感性分析情景假设

Table 5 Scenario assumptions for the long-term sensitivity analyses

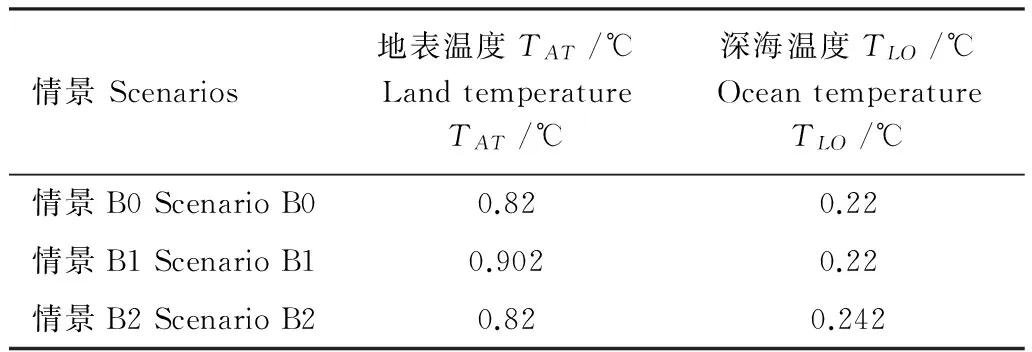
情景Scenarios地表温度TAT/℃LandtemperatureTAT/℃深海温度TLO/℃OceantemperatureTLO/℃情景B0ScenarioB00.820.22情景B1ScenarioB10.9020.22情景B2ScenarioB20.820.242

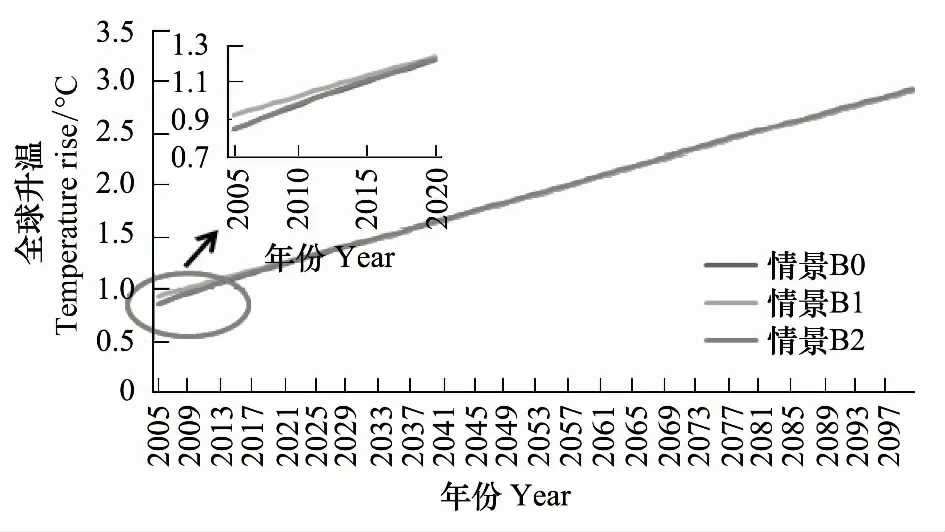
图8 气候响应模块长时间序列敏感度分析的升温比较Fig.8 Comparison of temperature rise in the long-term sensitivity analyses

因此，DICE/RICE气候响应模块的短期温度模拟对地表温度初值敏感性强，对深海温度初值敏感性较弱；而长期温度模拟对地表温度初值的敏感性下降，对深海温度初值的敏感性上升，但两者的敏感性均小于短时间序列下的敏感性，且在长时间序列下不同初值下的温度预测最终将出现收敛，即初值的差异对长期的温度预测影响可以忽略不计。

3.3 未来全球温度及大气二氧化碳浓度预测分析

建立IAM，最终的目的是对未来全球温度及大气二氧化碳浓度做出预测，以帮助制定一定温度控制目标下的全球减排方案。仍以2005—2100年的全球碳排放量数据，作为N1-N模型、N3-N模型和S-N模型的输入，分别模拟得到3个模型至2100年全球升温和全球二氧化碳浓度变化情景，分别如图9所示。

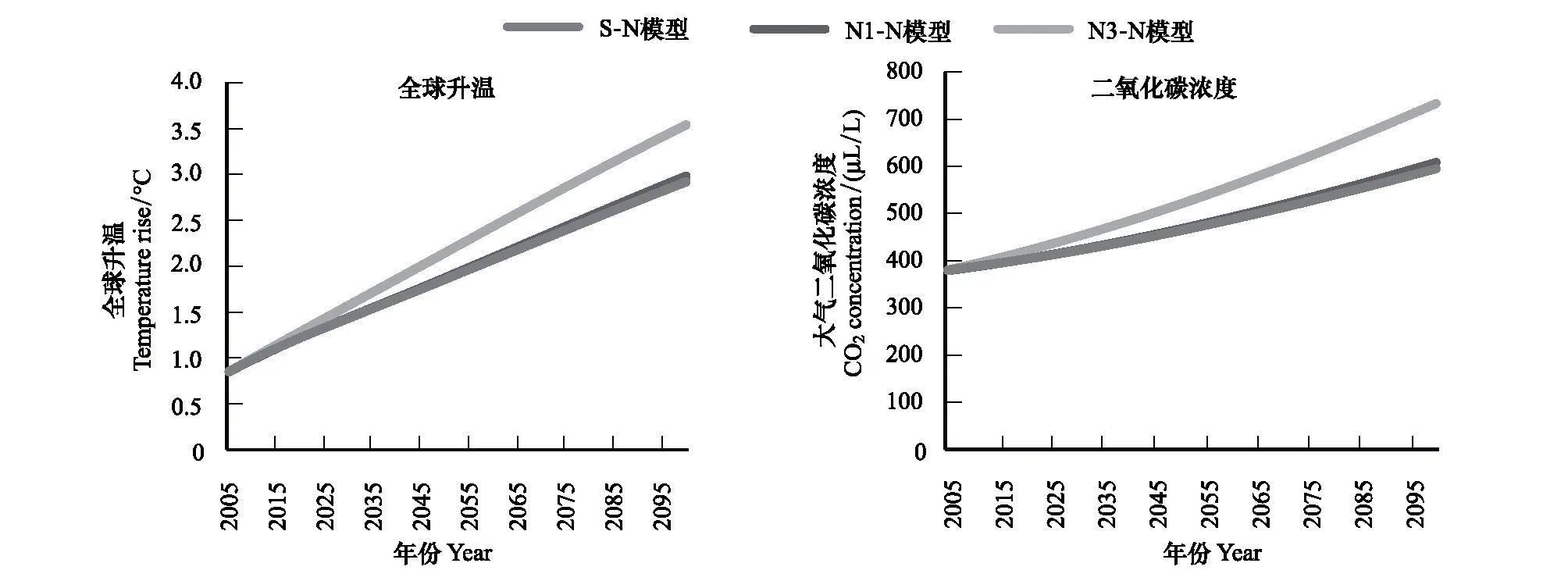
图9 2005—2100年全球升温和二氧化碳浓度预测Fig.9 Projection for temperature rise and CO2 concentration in 2005—2100

至2100年，N1-N模型、N3-N模型和S-N模型的温度预测值分别为2.98,3.54,2.91℃，二氧化碳浓度值分别为608.04,733.04,594.70μL/L。可以看到，3个模型的温度预测值均落在IPCC第四次评估报告得到的至本世纪末升温1.8℃—4.0℃的预测范围之内[27]，其中N3-N模型的预测温度值最高，比S-N模型获得的最低预测值高出0.62℃，而N1-N模型和S-N模型的预测结果相差很小，差值仅为0.07℃。而3个模型下全球二氧化碳浓度模拟结果也具有相似的排序。这里之所以在S-N模型下模拟得到2100年全球升温和二氧化碳浓度都最低，是由于Svirezhev碳循环模块考虑了陆地生态系统对二氧化碳的吸收作用，降低了大气二氧化碳含量，体现了陆地生态系统在碳循环建模中不可忽视的作用。

由于N3-N模型和S-N模型中的碳循环模块，即Nordhaus三层碳库模块和Svirezhev碳循环模块，都考虑了大气、陆地、海洋3个碳库，因此可以进一步比较两个模块的陆地和海洋碳库碳含量模拟值，如图10所示。在两个模型下，全球陆地生态系统的碳含量和海洋碳含量都逐年曾加，但进一步分析两个模型的陆地和海洋碳含量值，却发现两者存在较大的差别。

首先，Nordhaus三层碳库模型的陆地碳库碳含量小于Svirezhev碳循环模型的中陆地碳库的碳含量。而实际上，Nordhaus三层碳库模型中的陆地碳库是由陆地生物圈和海洋表层碳含量两部分组成，从理论上来说，其涵盖的范围大于Svirezhev碳循环模型中陆地生态系统的范围，但其模拟得到的碳含量值却小于Svirezhev模型。同时，IPCC研究表明陆地生态系统的碳含量约为2000GtC[28]，那么从数值上来看，Nordhaus三层碳库的模拟结果也远小于实际值，这也就导致了该模型的大气碳含量偏高，从而使其模拟得到的全球升温预测值也偏高。

其次，同样的情况也发生在图10中，可以看到Nordhaus三层碳库模型的碳含量远小于Svirezhev碳循环模型。目前研究表明深层海洋的碳含量约37000—40000GtC[28]，Svirezhev碳循环模型模拟值与该观测值接近，而Nordhaus三层模型的模拟值与该观测值偏离较大。造成Nordhaus三层碳库模型偏差较大的原因在于Nordhaus, Boyer[17]对于MLO的取值是与Bern碳循环模型校准的结果，而非实际观测意义上的值，也就是说Nordhaus三层模型中的深层海洋并非真实的深层海洋，那么该模型也就不是真正意义上的三层碳库模型。因此， Nordhaus三层碳库模型模拟的准确性仍值得商榷；而Svirezhev碳循环模型不仅将陆地生态系统细分为植被和土壤碳库，而且对各碳库都获得了较好的模拟结果。

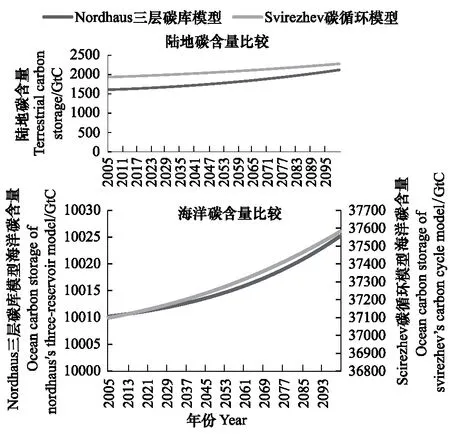
图10 陆地和海洋碳库碳含量预测Fig.10 Comparison of terrestrial and ocean carbon storage

总体而言，针对长期的气候变化预测，Nordhaus单层模型与Svirezhev碳循环模型在模拟结果上较为接近，但后者在碳循环机制上有了较显著的改进，不仅实现了动态的三层碳库循环模拟，而且进一步细化了陆地生态系统的固碳机制；而Nordhaus三层碳库模型虽然为三层碳库，但其陆地和海洋碳库的碳含量远小于各碳库碳含量的实际观测值，使该模型的准确性和可靠性大打折扣。

4 结论

对碳循环机制的正确建模是影响IAM结果的重要因素之一。本文分别将DICE/RICE模型中的Nordhaus单层模块、Nordhaus三层模块及Svirezhev碳循环模块与DICE/RICE模型的气候响应模块整合，构建了N1-N模型、N3-N模型、S-N模型，就3个模型对全球二氧化碳浓度、全球温度的模拟性能展开了比较分析。

以2001—2008年历史碳排放数据对3个模型进行校验，研究发现，3个碳循环模块对全球二氧化碳浓度变化的模拟在趋势性和准确性上都获得了比较好的结果，与实际值较为相似，其中以Svirezhev碳循环模块的标准误差最小，模拟性能相对较为突出；而DICE/RICE模型中的气候响应模块对全球温度变化的模拟准确度仍有待提高，同时，敏感性分析也发现，短期的温度模拟对地表温度初值敏感性强，长期的温度模拟对地表温度敏感度有所下降。

以MRICES模型模拟得到的2006—2100年碳排放量为模型输入，研究得到，N3-N模型对2100年温度的预测值最高，为3.54℃，这显著高于N1-N模型和S-N模型的预测值2.98℃, 2.91℃。S-N模型相对较低的温度预测值主要是由于Svirezhev碳循环模块考虑了陆地生态系统和海洋碳库对二氧化碳的吸收，降低了大气二氧化碳含量，这表明陆地生态系统和海洋碳库在碳循环中对固碳的显著贡献。

概括而言，基于对3个模型的比较分析，我们认为，在3个碳循环模块中，Svirezhev碳循环模型将陆地生态系统纳入到IAM的碳循环中，细化了IAM中碳循环机制的模拟，同时在大气二氧化碳含量模拟的趋势性和准确性上又获得了较好的结果，其模拟性能在3个模型中较为突出；Nordhaus三层碳库模型虽然纳入了陆地和海洋碳库，但并未能在模拟性能上对DICE/RICE模型的碳循环模块有显著改善，相反其对陆地和海洋碳库碳含量的模拟是不准确的，与实际观测值偏离较大；而Nordhaus单层碳库模型虽然模型较为简单，但该模型与Svirezhev碳循环模型的模拟结果均较为接近，说明该模型在对碳循环的简化抽象中保证了准确性，其模拟性能仍优于Nordhaus三层碳库模型。 总之，引入Svirezhev碳循环模型将在建模机制和模拟性能上对DICE/RICE模型的碳循环模块有所改进。

[1] Kelly D, Kolstad C. Integrated assessment models for climate change control // Folmer H, Tietenberg T, eds. The International Yearbook of Environmental and Resource Econoics: 1999/2000: A survey of Current Issues. Cheltenham, U. K.: Elgar, 1999: 171- 197.

[2] Nordhaus W D. Integrated Economic and Climate Modeling. New Haven: Yale University, 2011.

[3] van Vuuren D P, Lowe J, Stehfest E, Gohar L, Hof A F, Hope C, Warren R, Meinshausen M, Plattner G K. How well do integrated assessment models simulate climate change?. Climatic Change, 2011, 104(2): 255- 285.

[4] Warren R, Mastrandrea M D, Hope C, Hof A F. Variation in the climatic response to SRES emissions scenarios in integrated assessment models. Climatic Change, 2010, 201(3- 4): 671- 685.

[5] Nordhaus W D. Rolling the ‘DICE’: An optimal transition path for controlling greenhouse gases. Resource and Energy Economics, 1993, 15(1): 27- 50.

[6] Nordhaus W D, Yang Z. A regional dynamic general-equilibrium model of alternative climate-changes strategies. American Economic Review, 1996, 86(4): 741- 765.

[7] Plambeck E L, Hope C, Anderson J. The model: integrating the science and economics of global warming. Energy Economics, 1997, 19(1): 77- 101.

[8] Tol R S J. Spatial and temporal efficiency in climate policy: applications of FUND. Environmental and Resource Economics, 1999, 14(1): 33- 49.

[9] Nordhaus W D. The “DICE” Model: Background and Structure of a Dynamic Integrated Climate-Economy Model of the Economics of Global Warming. New Haven: Yale University, 1992.

[10] Nordhaus W D. Optimal greenhouse-gas reductions and tax policy in the “DICE” model. American Economic Review, 1992, 83(2): 313- 317.

[11] Buonanno P, Carraro C, Galeotti M. Endogenous induced technical change and the costs of Kyoto. Resource and Energy Economics, 2003, 25(1): 11- 34.

[12] van der Zwaan B C C, Gerlagh R, Klaassen G, Schrattenholzer L. Endogenous technological change in climate change modelling. Energy Economics, 2002, 24(1): 1- 19.

[13] Popp D. ENTICE-BR: The effects of backstop technology R&D on climate policy models. Energy Economics, 2006, 28(2): 188- 222.

[14] Wu J, Zhu Q T, Wang Z. Modeling the influence of R&D expenditures on global climate protection. Studies in Science of Science, 2012, 30(4): 517- 525.

[15] Wang Z, Li H Q, Wu J, Gong Y, Zhang H B, Zhao C. Policy modeling on the GDP spillovers of carbon abatement policies between China and the United States. Economic Modelling, 2010, 27(1): 40- 45.

[16] Pizer W A. The optimal choice of climate change policy in the presence of uncertainty. Resource and Energy Economics, 1999, 21(3- 4): 255- 287.

[17] Nordhuas W D, Boyer J. Warming the World: Economic Models of Global Warming. Massachusetts, US: MIT Press, 2000.

[18] Yu G R, Fang H J, Fu Y L, Wang Q F. Research on carbon budget and carbon cycle of terrestrial ecosystems in regional scale: a review. Acta Ecologica Sinica, 2011, 31(19): 5449- 5459.

[19] Fang J Y, Chen A P, Peng C H, Zhao S Q, Ci L J. Changes in forest biomass carbon storage in China between 1949 and 1998. Science, 2001, 292(5525): 2320- 2322.

[20] Fang J Y, Piao S L, Zhao S Q. The carbon sink: the role of the middle and high latitudes terrestrial ecosystems in the northern hemisphere. Acta Phytoeclogical Sinica, 2001, 25(5): 594- 602.

[21] Liu Y C, Yu G R, Wang Q F, Zhang Y J. Huge carbon sequestration potential in global forests. Journal of Resources and Ecology, 2012, 3(3): 193- 201.

[22] Svirezhev Y, Brovkin V, von Bloh W, Schellnhuber H J, Petschel-Held G. Optimisation of reduction of global CO2emission based on a simple model of the carbon cycle. Environmental Modeling and Assessment, 1999, 4(1): 23- 33.

[23] Wang Z, Wu J, Zhu Y B, Yue Q. Economic Research on Climate Protection. Beijing: Science Press, 2010.

[24] Nordhaus W D. RICE2010. [2012- 12-08]. http://nordhaus.econ.yale.edu/RICEmodels.htm.

[25] Annual global temperature anomalies. National Ocean and Atmospheric Administration. [2012- 12-01].htm.http://www.ncdc.noaa.gov/oa/climate/research/anomalies/index.html

[26] Wang Z, Wu J, Li G Q, Zhang H B, Wang L J. Using simulation to assess climate-change strategies for global participation. Acta Ecologica Sinica, 2009, 29(5): 2407- 2417.

[27] IPCC. Climate Change 2007: Synthesis Report. Cambridge, U. K.: Cambridge University Press, 2007.

[28] IPCC. Climate Change 2001: The Scientific Basis. Cambridge, U. K.: Cambridge University Press, 2001.

参考文献:

[14] 吴静, 朱潜挺, 王铮. 研发投资对全球气候保护影响的模拟分析. 科学学研究, 2012, 30(4): 517- 525.

[18] 于贵瑞, 方华军, 伏玉玲, 王秋凤. 区域尺度陆地生态系统碳收支及其循环过程研究进展. 生态学报, 2011, 31(19): 5449- 5459.

[20] 方精云, 朴世龙, 赵淑清. CO2失汇与北半球中高纬度陆地生态系统的碳汇. 植物生态学报, 2001, 25(5): 594- 602.

[23] 王铮, 吴静, 朱永彬, 乐群. 气候保护的经济学研究. 北京: 科学出版社, 2010.

[26] 王铮, 吴静, 李刚强, 张焕波, 王丽娟. 国际参与下的全球气候保护策略可行性模拟. 生态学报, 2009, 29(5): 2407- 2417.

Comparison of the carbon cycle models in DICE/RICE

WU Jing1, ZHU Qianting2, LIU Changxin1, WANG Zheng1,3,*

1InstituteofPolicyandManagement,ChineseAcademyofSciences,Beijing100190,China2SchoolofBusinessAdministration,ChinaUniversityofPetroleum,Beijing102249,China3KeyLaboratoryofGeographicalInformationScience,MinistryofStateEducationofChina,EastChinaNormalUniversity,Shanghai200062,China

Modeling of the carbon cycle is one of the most important issues in research of the Integrated Assessment Model (IAM). The carbon-cycle module can not only implement the carbon balance among different carbon reservoirs, but can also provide an interface for climate adaptation and mitigation through management of carbon sinks and land use change. As one of the most popular IAMs in the world, the dynamic integrated model of climate and the economy / regional integrated model of climate and the economy (DICE/RICE) model has two versions of carbon-cycle models. These are the solo-reservoir (N1-N) and three-reservoir (N3-N) models. However, there is an obvious drawback of the two models. This is that terrestrial carbon storage is not considered. Therefore, this work examines the effectiveness of the carbon-cycle models within DICE/RICE, and compares the two models with another carbon-cycle model presented by Svirezhev (S-N model).By inputting global historical emission data into the three models (N1-N, N3-N and S-N), we obtain simulations of historical temperature and CO2concentration during 2001 to 2008. The results are calibrated with observed historical CO2concentrations and temperature changes, by developing a correlation test. The results show that correlations of CO2concentration based on the N1-N, N3-N and S-N models are 0.9967, 0.9971 and 0.9970, respectively, and corresponding correlations of temperature are 0.452, 0.447 and 0.451. It was found that there was a significant correlation between simulated and observed CO2concentration data, but simulated and observed temperature data were uncorrelated. This result is verified by an analysis of variance for the simulated and observed data. Although the correlations between the N1-N, N3-N and S-N models are very similar, the standard errors of CO2concentration data are 2.53, 2.76 and 0.89, respectively. This shows that the simulation based on the S-N model is much more accurate in relation to the observed data. The N1-N, N3-N and S-N models were used to project climate change by the year 2100, for which the temperatures are 2.98, 3.54℃ and 2.91℃, respectively, and the CO2concentrations are 608.04,733.04, 594.70 ppm, respectively. Projections with smallest values were produced by the terrestrial ecosystem and ocean carbon reservoir represented in the S-N model. This indicates that when carbon is absorbed by the terrestrial ecosystem and ocean in that model, atmospheric carbon is less than those in the other models. Although there are also three reservoirs in the DICE/RICE N3-N model, its results deviate substantially from actual observations. The climate response model used by DICE/RICE was also found to be sensitive to the initial value of land surface temperature, when applied in a short-term projection. However, the sensitivity becomes weaker when applied in a long-term projection. Therefore, the S-N model turns out to be superior to the other models in terms of a much more detailed model mechanism and more accurate modeling performance. In spite of the simplification of the N1-N model, its simulation results are still better than those of the N3-N, in which carbon in the biosphere and ocean is significantly different from observations.

IAM; carbon cycle; terrestrial ecosystem; carbon reservoir; Dynamic Integrated model of Climate and the Economy (DICE); Regional dynamic Integrated model of Climate and the Economy (RICE)

国家重大研究计划(973)项目(2012CB955800); 中国科学院战略性先导科技专项 (XDA05150900)

2013- 02- 25; 网络出版日期:2014- 03- 14

10.5846/stxb201302250298

*通讯作者Corresponding author.E-mail: wangzheng@casipm.ac.cn

吴静，朱潜挺，刘昌新，王铮.DICE/RICE模型中碳循环模块的比较.生态学报,2014,34(22):6734- 6744.

Wu J, Zhu Q T, Liu C X, Wang Z.Comparison of the carbon cycle models in DICE/RICE.Acta Ecologica Sinica,2014,34(22):6734- 6744.