桩径和端形对粗粒土破碎的模拟分析★

胡舫瑞 邵晓泉

(中国地质大学(武汉)工程学院，湖北 武汉 430071)

桩径和端形对粗粒土破碎的模拟分析★

胡舫瑞 邵晓泉

(中国地质大学(武汉)工程学院，湖北 武汉 430071)

基于二维颗粒流理论，采用特定的破碎法则，对不同桩尖形状和不同桩径的沉桩过程进行了离散元模拟，对桩周地基土颗粒的破碎及其对沉桩的宏观影响进行了详细的分析研究，得出了一些有意义的结论。

桩尖形状，桩径，破碎，离散单元法

0 引言

早在20世纪60年代，颗粒破碎现象就引起了岩土工程师的广泛关注。研究表明，易发生颗粒破碎的情况主要有两种：一是诸如强风化花岗岩、火山灰和碳酸盐类砂土颗粒自身强度较低，在常应力下即可发生明显的颗粒破碎现象[1]；二是其颗粒强度本身很高，但是处于高应力状态，诸如铁路路床、土石坝和桩基础等[2]。

随着计算机功能的不断增强，从细观角度辅助颗粒破碎的研究成为可能。颗粒流作为一种简化的离散单元法，在20世纪就开始广泛应用于细观研究中，桩土相互作用一直是人们研究的重点，以周健为代表的众学者近十年实验结合数值分析对桩土相互作用展开较系统的研究[3，4]，但是在桩土中考虑颗粒破碎的研究却少有。并且目前基于pfc离散元方法考虑颗粒破碎的方式主要有两种，一种是通过将一定数量的小球/圆盘按一定的方式组合粘结起来组成不同形状的颗粒簇，粘结键的断裂即代表该颗粒发生了破碎[5]；另一种则是基于单个颗粒，当其所受到的接触力满足一定条件时，则认为颗粒发生了破碎[6]。两种考虑方法各有优缺点。

本文选择第二种考虑颗粒破坏的方式，基于颗粒流理论，对闭口桩的沉桩过程中的颗粒破碎进行了数值模拟分析。模拟中具体对桩端形状和桩径对颗粒破碎及沉桩阻力进行了研究，在分析过程中克服了传统连续介质力学模型的宏观连续性假设，从颗粒尺度探讨闭口管桩沉桩过程中宏细观力学机理和颗粒破碎的发展模式。

1 颗粒破碎准则与破坏模式

颗粒破坏模式参考前人研究成果[6,7]，认为单个颗粒的破碎与该颗粒的配位数相关。此处配位数即是指颗粒接触点的个数，是描述颗粒材料性态的一个重要微观参数。前人研究认为C>4不再发生破碎，破坏模式为与配位数相关的较严重的破裂，并未考虑研磨破碎，因此本文增加了与配位数相关的破坏模式，认为C=5时颗粒发生了程度较轻的研磨破坏，具体破坏模式如图1所示。

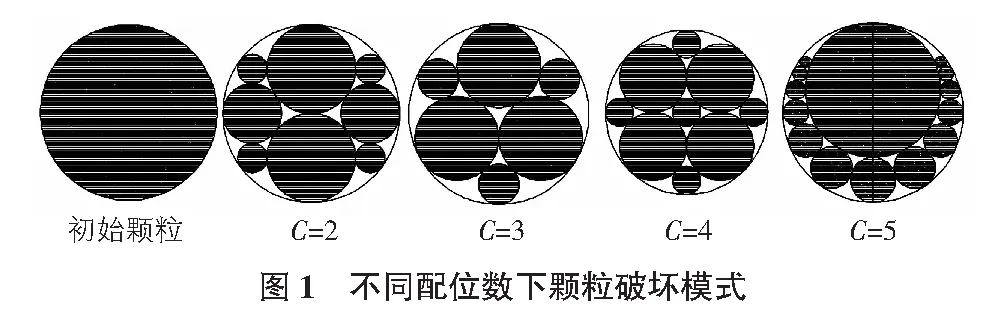
C∈[2，5]时颗粒发生破碎，破碎成几个大粒径的主要颗粒和小颗粒，如图1所示，C=2时颗粒破坏为含有两个大颗粒的八颗粒群体，C=3时颗粒破坏为含有两种尺寸的六个颗粒，C=4时颗粒破坏为含有两种尺寸的九个颗粒，当C=5时我们认为颗粒发生了研磨破坏，破坏模式为含有一个超大颗粒的群体。

借鉴Lobo-Guerrero和Vallejo(2005)等采用的破坏准则，颗粒在受多个力平衡时，其拉伸应力为:

σt=2Pmax/πLD。

其中，Pmax为圆盘所受接触力中最大的；L为圆盘厚度；D为圆盘直径。

假设半径为1 mm的圆盘抗拉强度σmax1 mm为一定值，从而可得一般粒径颗粒的抗拉强度σmax(r)为：

σmax(r)=σmax1 mm[r]-1。

当配位数C∈[2，5]，且σt>σmax(r)时，颗粒即发生破碎[7]。

必须指出的是上述给出的与配位数相关的破碎模式是在缺少试验资料的情况下提出来的，目的是考察破碎对沉桩结果的影响[6]。

2 模型的建立

选取不同的桩尖形状和不同桩径的闭口管桩进行颗粒流模拟。模型尺寸和试验材料参考江浩等(2010)所做的模型桩实验[8]，通过对称性简化为二维模型，模型箱尺寸为700 mm×900 mm，桩径为30 mm，桩长为500 mm，为了作对比，桩尖形状选择半圆形和不同角度的桩尖，桩径为20 mm和40 mm的桩。如果按试验时所用钙质砂的级配曲线生成颗粒，则颗粒数量巨大，直接影响计算的效率，参考周健等(2012)的处理方式，桩周及桩端附近采用较小的砂土粒径，离桩较远处采用较大粒径，以便使这些区域的颗粒与实际砂土的工程特性相接近[3]。将周围颗粒用较大粒径的颗粒进行替换，如图2所示，各区域呈轴对称分布，区域1颗粒粒径为1 mm～2 mm，区域2颗粒粒径为4 mm～6 mm，区域3颗粒粒径为8 mm，区域4颗粒粒径为12 mm。

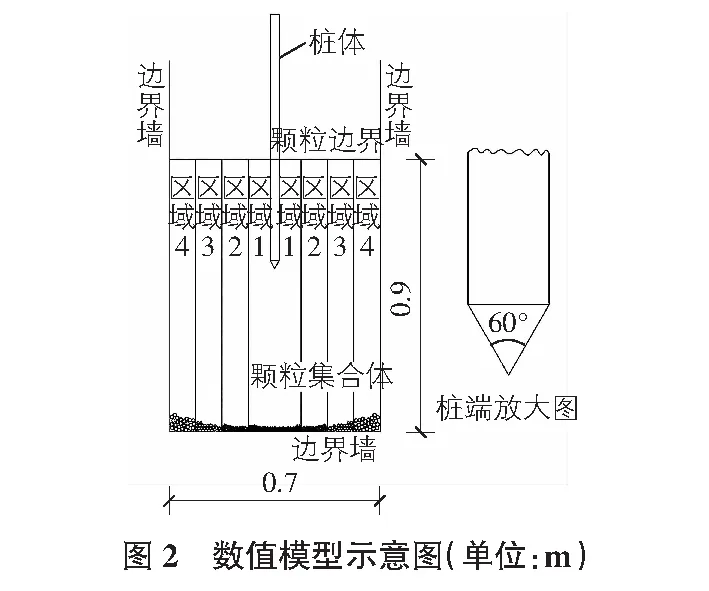
试验材料参数通过对比文献中钙质砂力学性质为依据，通过双轴试验与室内三轴试验对比分析，反复验证，最终确定颗粒的密度为2.79 g/cm3，切向刚度为6.4×108N/m，法向刚度为6.4×108N/m，摩擦系数为0.6，孔隙比为0.20。管桩采用墙体模拟，在沉桩过程中不可破坏，同时参考周健等人的文章，桩体刚度不小于土体颗粒的10倍，最终确定桩体的颗粒密度为2.9 g/cm3，切向刚度6.4×1010N/m，法向刚度6.4×1010N/m，摩擦系数0.9。

沉桩过程中，圆盘本身并不会发生破坏，采用Fish语言编写特定的程序，在颗粒受力和接触数达到一定条件时，则认为颗粒发生破碎，根据不同的接触数和记录下来的颗粒粒径对颗粒进行替换，即删除现有的颗粒，按等比例替换为新的颗粒集合。为了控制破碎量，假定半径为1 mm的颗粒破碎时，其极限抗拉应力为3 MPa。一般认为颗粒破碎到一定程度即不会再发生破碎，模拟时取极限破碎粒径为1 mm。

以一定的速度静压桩体，同时监测压桩过程中桩体受力和颗粒中的最大颗粒数，为了对桩沉入过程进一步了解，在桩下沉0.05 m,0.1 m,0.3 m和0.5 m时自动保存计算结果，便于对沉桩过程进行分析。

3 桩的沉入过程分析

桩端阻力与桩侧阻力相比，桩端受力较大，故可以判断颗粒破碎主要是由桩端对土体的挤压造成的。如图3所示，桩端阻力和桩侧阻力均随着贯入深度的增加而增加，桩端阻力在压桩初期急剧增加，随着压桩的进行，桩端阻力增加缓慢，最后桩端阻力得到完全发挥，阻力值在一定范围内波动。桩侧阻力随着桩的下沉均匀增加，主要受桩入土深度的影响。仔细对比不难发现地基土中最大颗粒数与桩端阻力的波动密切相关，每当发生较剧烈的颗粒破碎，颗粒数量急剧增加，而桩端阻力则发生较大的突降，然后随着压桩的深入，桩端阻力又开始进一步增加，直到下一次剧烈下降。

4 桩端形状的测试结果

图4为不同沉入深度下不同桩尖形式的管桩桩周颗粒破碎情况，不难发现，颗粒破碎发生于整个沉桩过程，随着压桩的深入，颗粒破碎越严重。对比桩尖角为60°,90°和120°不同深度的桩周颗粒分布情况可以发现，随着桩尖角度的增加，桩的排土能力越差，桩尖颗粒破碎范围增加，在相同的沉桩速度下，桩端颗粒受力越大，破碎越严重。半圆形与平底桩桩底颗粒破碎范围角含有一定角度的锥形桩大，说明锥形桩尖角半圆形和平底桩更易压入土体。

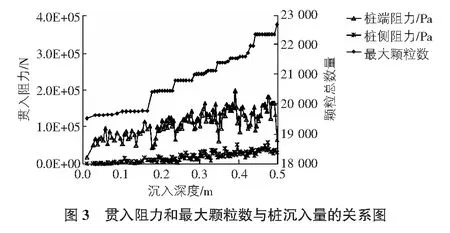
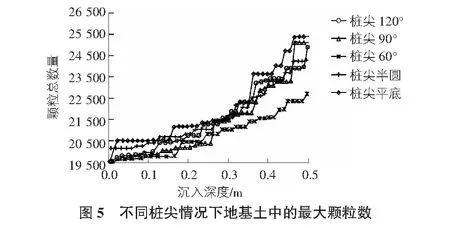
图5为不同桩尖情况下地基土颗粒体系中的最大颗粒数，桩尖角为60°时，颗粒破碎明显弱于其他情况，说明桩尖角度越小，桩的排土性越好，对地基土颗粒的集中力越小。压桩初期，桩尖为平底和半圆形时，颗粒总数量突变明显，主要是由于平底和半圆形桩端与颗粒接触数多，排土速度不快，桩端颗粒受力较大，导致颗粒破碎严重。对比图5中曲线，半圆形桩尖除在沉桩初期颗粒总数发生突变外，整个沉桩过程中颗粒总数平缓增加，相较其他曲线而言，颗粒数波动较小，桩受力更平稳。当然由于破坏准则中规定颗粒破坏替换随接触数的不同而变化，不能通过颗粒数量的多少来简单判断颗粒破碎的严重程度，而需要采用专门的颗粒破碎指标来探讨。

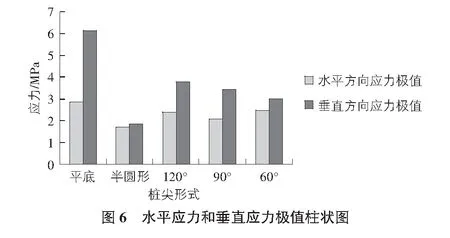
通过监测圆监测桩周附近应力情况可知，不同桩尖形式下应力分布具有相似性，在桩底均形成了应力核，但应力的大小和分布情况因桩尖形式而不同，图6为桩下沉深度为0.4 m时不同桩尖形式下，地基土中的水平和垂直应力极值柱状图。从图6中不难看出，桩尖为平底的地基土中应力极值最大，而半圆形桩尖的应力极值最小，随着桩尖角度的减小，垂直方向应力极值逐渐减小，综合来看，半圆形桩受力较小，且均匀。

5 桩径的影响分析

图7为不同桩径地基土中颗粒总数量随沉入深度关系图，在桩下沉深度小于0.25 m时，颗粒总数量并不因桩径不同而有明显差别，主要是由于颗粒在浅层受到的应力小，颗粒运动受到的限制相对较小，可以通过颗粒的压缩挤密和移动来重新调整。下沉深度超过一定值后，颗粒总数量区别明显，表现为桩径越大，颗粒总数量越多。

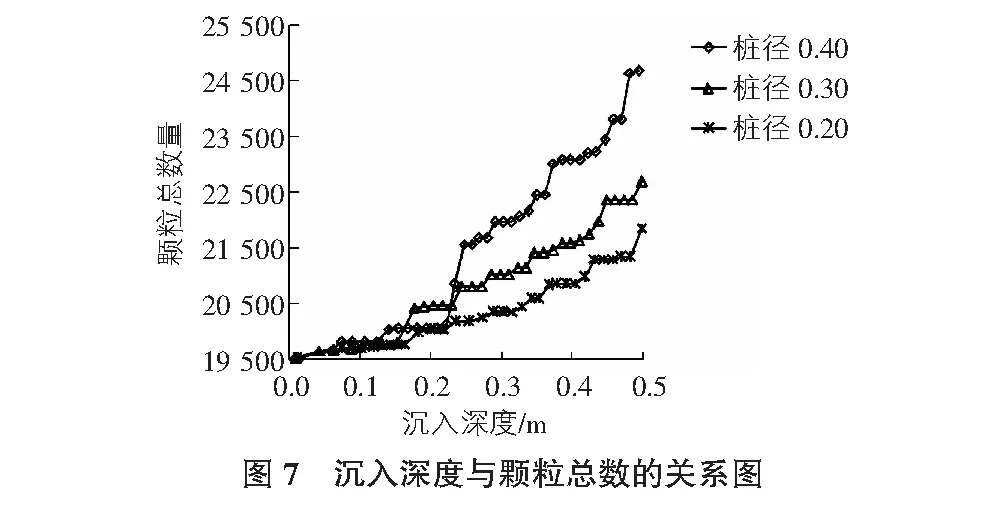
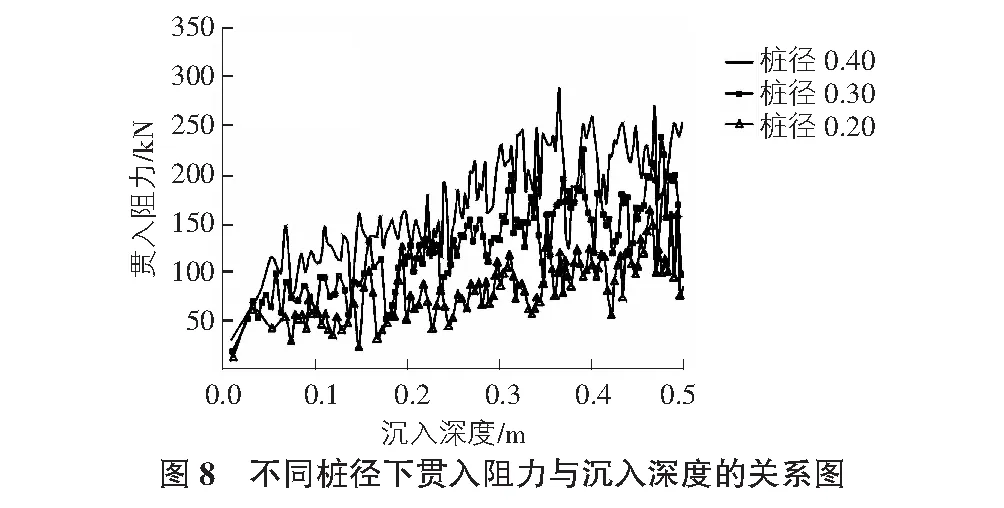
图8为不同桩径下贯入阻力与沉入深度的关系图，贯入阻力随沉入深度具有较大的波动性，压桩初期贯入阻力急剧增加，随着贯入深度的增加，贯入阻力增长速率减小。但整体来看，桩径越大，相同贯入深度下贯入阻力越大。

6 结语

1)桩端阻力和桩侧阻力均随着贯入深度的增加而增加，桩端阻力在压桩初期急剧增加，随着压桩的进行，桩端阻力增加缓慢。桩侧阻力随着桩的下沉均匀增加。

2)地基土中颗粒破碎与桩端阻力的波动密切相关。

3)在相同的沉桩速度下，桩尖角度越大，排土能力越差，桩端颗粒受力越大，破碎越严重。锥形桩尖角半圆形和平底桩更易压入土体。

4)半圆形桩尖的桩体受力更平稳。

5)桩径越大，相同贯入深度下颗粒破碎越严重，贯入阻力也就越大。

[1] 张家铭，蒋国盛，汪 稔.颗粒破碎及剪胀对钙质砂抗剪强度影响研究[J].岩土力学，2009,30(7):2043-2048.

[2] 杜 俊，侯克鹏，梁 维，等.粗粒土压实特性及颗粒破碎分形特征试验研究[J].岩土力学，2013,34(S1):155-161.

[3] 周 健，李魁星，郭建军，等.分层介质中桩端刺入的室内模型试验及颗粒流数值模拟[J].岩石力学与工程学报，2012(2):375-381.

[4] 张伟丽，蔡 健，林奕禧，等.桩径和桩距对搅拌桩复合地基影响的研究[J].科学技术与工程，2009,9(16):4703-4708.

[5] 邵 磊，迟世春，王振兴.基于裂缝扩展的堆石料流变细观模型[J].岩土工程学报,2013,35(1):66-75.

[6] 楚锡华，周伦伦，徐远杰.可破碎颗粒材料组构各向异性演化及剪胀性的离散元模拟[A].颗粒材料计算力学会议[C].2012.

[7] Lobo-Guerrero S,Vallejo L E.Discrete Element Method Evaluation of Granular Crushing Under Direct Shear Test Conditions[J].Journal of Geotechnical and Geoenvironmental Engineering，2005,131(10):1295-1300.

[8] 江 浩，汪 稔，吕颖慧，等.钙质砂中模型桩的试验研究[J].岩土力学，2010,31(3):780-784.

On simulation analysis of pile diameter and end relief on coarse-grained soil crushing★

HU Fang-rui SHAO Xiao-quan

(Engineering College, China University of Geosciences(Wuhan), Wuhan 430071, China)

Based on the two-dimensional granular flow theory, adapts crushing rule, the paper undertakes the discrete element simulation in the pile sinking process with different pile points and pile diameters, undertakes the detailed analysis and research on the pile surrounding foundation soil granular and its macroscopic influence on pile sinking, and has some meaningful conclusion.

pile toe shapes, pile diameter, crushing, discrete element method

1009-6825(2014)31-0072-03

2014-05-12★：2013年中国地质大学(武汉)教学实验室开放基金资助项目

胡舫瑞(1988- )，男，在读硕士； 邵晓泉(1990- )，女，在读硕士

TU473.1

A