卫星编队飞行相对绕飞控制策略

姜 宇 李恒年 潘立公 胡 静 宝音贺西

1.宇航动力学国家重点实验室，西安 710043 2.清华大学航天航空学院，北京 100084



卫星编队飞行相对绕飞控制策略

姜 宇1,2李恒年1潘立公1胡 静1宝音贺西2

1.宇航动力学国家重点实验室，西安 710043 2.清华大学航天航空学院，北京 100084

提出了一种能考虑复杂摄动模型的卫星编队飞行相对绕飞控制策略，该策略仅需进行切向和法向控制，控制律不需要改变推力大小和方向，不需要进行卫星的姿态机动，适用范围广。对绕飞角、绕飞中心、绕飞基线等编队构形参数的控制精度高，对绕飞角的控制误差可达0.05°以下，绕飞挠率控制到0.001以下。此外，绕飞中心、绕飞角、绕飞基线、最小距离、最大距离均可稳定地保持，控制后编队构形稳定性好，有利于延长保持控制的周期，节约推进剂的消耗。该策略首次实现了对绕飞中心和绕飞挠率的控制。

卫星编队飞行；绕飞曲率；绕飞挠率；绕飞控制；相对控制；控制策略

卫星编队飞行可用于合成孔径雷达、反卫星相对伴飞、科学试验、深空探测等诸多空间技术领域。合成孔径雷达(Synthetic Aperture Radar，SAR)卫星编队[1-2]具有全天候远距离高分辨率成像、干涉测高、移动目标识别定位等优点，具有广泛的用途。特别是由于SAR不易受气候和日照条件的影响，能穿透云层昼夜工作，可对地面、海洋、空间移动目标进行全天候侦查，故而由合成孔径雷达卫星组成的编队实施空间侦察任务将逐渐成为未来侦查卫星的主要发展方向之一。绕飞式的编队构形是SAR卫星编队主要采用的编队构形[1]。编队构形的控制可分为编队控制目标的计算和编队控制策略的计算，前者即编队构形的设计计算。

Schaub等[3-4]通过轨道平根数给出了一种J2不变相对轨道条件(J2Invariant Relative Orbit)，并基于平根数和该条件，给出了一种建立在Lyapunov稳定性基础上的编队控制方案。由于该方案是基于轨道平根数的，故无法进行圆形绕飞编队、Pendulum编队等[5-6]的控制。Amico 和 Montenbruck在2008年给出了一种绕飞式编队构形的相对控制方法[7]，不含绕飞角的控制，对于绕飞基线在千米量级、轨道高度500km左右的绕飞构形，控制后若要求编队构形漂移不超过250m，则理论上自然式的无控制相对运动可保持30d左右。杨海峰和尹路明[11]给出了一种针对平均轨道根数进行控制的近地轨道卫星编队构形保持方法，此外还有基于相对运动方程的编队构形反馈控制方法[9-10]。这些编队控制方法无法叠加复杂的高精度引力场模型，优点是易于实施；有适用于短期的无具体构形要求的卫星编队[3-4,11-13]，也有适用于有具体构形要求的卫星编队[7]。

实际的卫星编队构形的控制要求为：控制算法易于实施；控制精度高，控制算法中能考虑复杂的高精度地球引力场模型、大气阻力及日月引力摄动等以便于控制后的相对构形尽可能长期地稳定；能对绕飞角、各方向绕飞基线等精细参数进行控制。

针对相对绕飞控制问题，本文提出了一种考虑复杂摄动模型的卫星编队飞行相对绕飞控制策略，不仅可对绕飞角、绕飞中心、绕飞基线等编队构形参数进行控制，而且控制精度极高。控制后编队构形稳定性好，编队构形参数如绕飞中心、绕飞角、最小距离、最大距离等均可稳定地保持，有利于延长保持控制的周期，节约推进剂的消耗。并且首次实现了对绕飞中心和绕飞挠率的控制。本文提出的编队相对绕飞控制策略仅需进行切向和法向的控制，控制律不需要改变推力的大小和方向，不需要进行卫星的姿态机动，适用范围广。

1 相对运动计算模型

1.1 相对运动动力学模型

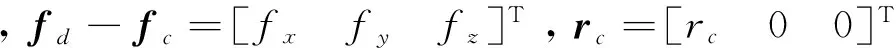
(1)

这是一个精确的相对运动动力学模型，通过对它的化简可以得到一些简化的近似模型。文献[8]的Clohessy-Wiltshire方程模型和文献[9]的Lawden方程模型都是其特例。若考虑近距离编队情形，即可由式(1)化简为Lawden方程模型；若考虑近距离编队情形，且令偏心率为0，则可由式(1)化简为Clohessy-Wiltshire方程模型。

根据Vadali[10]可得：

(2)

(3)

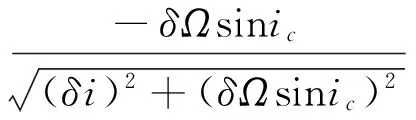
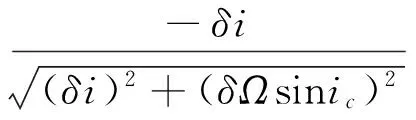
令δλ+δΩcosic=0，则由式(3)可得副星d相对主星的位置矢量在主星轨道坐标系C-xyz各轴表示为

(4)

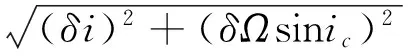
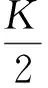
(5)

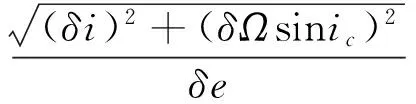
1.2 绕飞参数计算

副星相对主星的绕飞轨迹动量矩矢量为

H=R×V

(6)

式中，R为副星相对位置矢量在主星轨道坐标系的分量，V为副星相对速度矢量在主星轨道坐标系的分量，R和V均由式(1)计算。

绕飞平面同Cyz平面、Cxz平面以及Cxy平面的夹角α，β，γ分别为

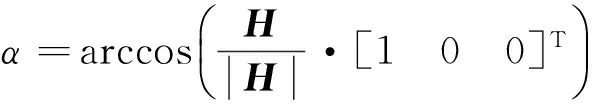
(7)

式中“·”表示内积。

绕飞曲率是表征编队相对运动轨迹弯曲程度的物理量，绕飞挠率是表征编队相对运动轨迹偏离平面运动程度的物理量。绕飞曲率k和绕飞挠率τ按照下式计算

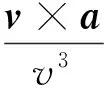
(8)

1.3 编队绕飞控制目标计算

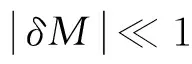
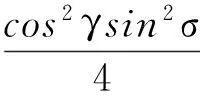
(9)

令

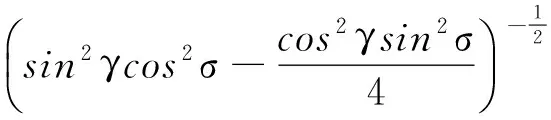
(10)

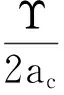
(11)

令ε=-ωc或ε=π-ωc，则其余轨道根数差按照式(12)计算

(12)

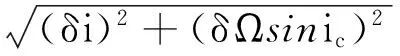
一般的编队构形设计，都将编队卫星的半长轴差设计[1-13]为0，由于复杂摄动力的作用，为了保证编队卫星在沿飞行方向不发生漂移，编队卫星的半长轴差一般不能设计为0；若将编队卫星的半长轴差设计为0，则对于几千米左右的编队基线，其构形的漂移速度很快，一般3～4d就需要进行构形保持控制，控制周期最长也不超过30d左右，文献[7]设计的编队理论上最长的控制周期为30d左右。下面给出半长轴差精确设计的方法。通过对相对位置在一个轨道周期内积分，计算绕飞中心，叠加高精度的摄动模型，对编队卫星的轨道进行外推，计算Nk圈以后的绕飞中心沿飞行方向即Cy轴的漂移量ΔL，通过下式迭代修正半长轴差

(13)

其中，k为迭代次数，一般可令Nk逐渐增大，k=3～5次，即可获得满意的结果，理论上轨道平面内的控制周期可达2年以上。

2 绕飞控制方法

假定发动机工作的过程中推力为常值且姿态无误差，发动机连续工作的时间为Δt，对应的工作弧段长度为Δu，弧段中点为u0，V是轨道速度，则当发动机仅提供切向推力T，受到影响的是a,e,w，其控制增量为

(14)

当发动机仅提供法向推力N时，i,Ω将发生变化但不影响a,e,ω，控制增量为

(15)

通过平面内2次横向速度增量控制,Δa,Δex和Δey的控制方法为[14]：

(16)

(17)

此时，速度增量及控制时刻轨道幅角的计算公式为

(18)

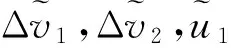
(19)

由此可达到对编队卫星之间的Δa,Δex,Δey和ΔL均进行控制的目的。

3 控制策略算例

摄动模型考虑：地球引力场采用JGM-3模型并取20×20阶，太阳引力和月球引力，大气阻力，太阳光压。设有A，B两个卫星需要进行编队飞行的相互绕飞控制。历元时刻取北京时间2012年06月01日07时00分00秒。

m表示卫星总质量，S表示截面积，mP表示推进剂质量，P表示推进剂箱压，CR表示光压系数，CD表示大气阻力系数。推力标定系数取1.0，设卫星轨道根数当前圈数为第1圈，要求平面内控制在第3，5，7圈进行，平面外控制在第6圈进行。要求平面内最大编队基线取为4000.0m，编队绕飞平面与当地水平面的夹角为34.0°，平面外采取降轨控制。每次控制最大推进时长约束为500s，控制过程中的最小安全距离约束为200m。控制时间要求约束在北京时间8～23h之间。要求控制后水平绕飞角控制误差约束为±1°，绕飞挠率小于0.005。要求绕飞中心在沿迹方向的分量相对基线长度的偏离小于5.0%，即小于200m。一般可取保持控制门限为绕飞中心在沿迹方向分量的绝对值大于平面内最大编队基线的20%～50%，如果平面内最大编队基线取为4.0km，则保持控制门限为绕飞中心在沿迹方向分量的绝对值大于0.8～2.0km。本文所述算法既可以进行编队绕飞构形形成控制策略的计算，也可进行编队绕飞构形保持控制策略的计算。

首先进行编队绕飞构形的设计，根据设计结果进行编队绕飞控制策略的计算，根据最终控制结果，进行控制后编队构形的预报。

计算得设计需求为δe=0.000285，δM=0.003442°，K=1.529771。据此设计的满足条件的副星目标轨道根数有2组，如下所示

表1 编队相对构形设计结果

构形设计结果如表1所示，可见满足设计要求的副星轨道有2个。其中水平绕飞角为编队相对绕飞平面与当地水平面的夹角，轨道面绕飞角为编队相对绕飞平面与主星轨道面的夹角，法平面绕飞角为编队相对绕飞平面与主星轨道面的子午面之间的夹角。水平绕飞角误差最大为0.058°，绕飞方向or，ot，on分别为相对绕飞轨迹法线方向在主星CW坐标系的三轴分量。

考虑20×20阶地球引力场模型、日月引力、大气阻力、太阳光压，按照需求和编队构形设计结果，进行编队绕飞控制策略的计算，将副星按照设计的副星轨道1进行相对控制。控制策略计算结果如表2所示。

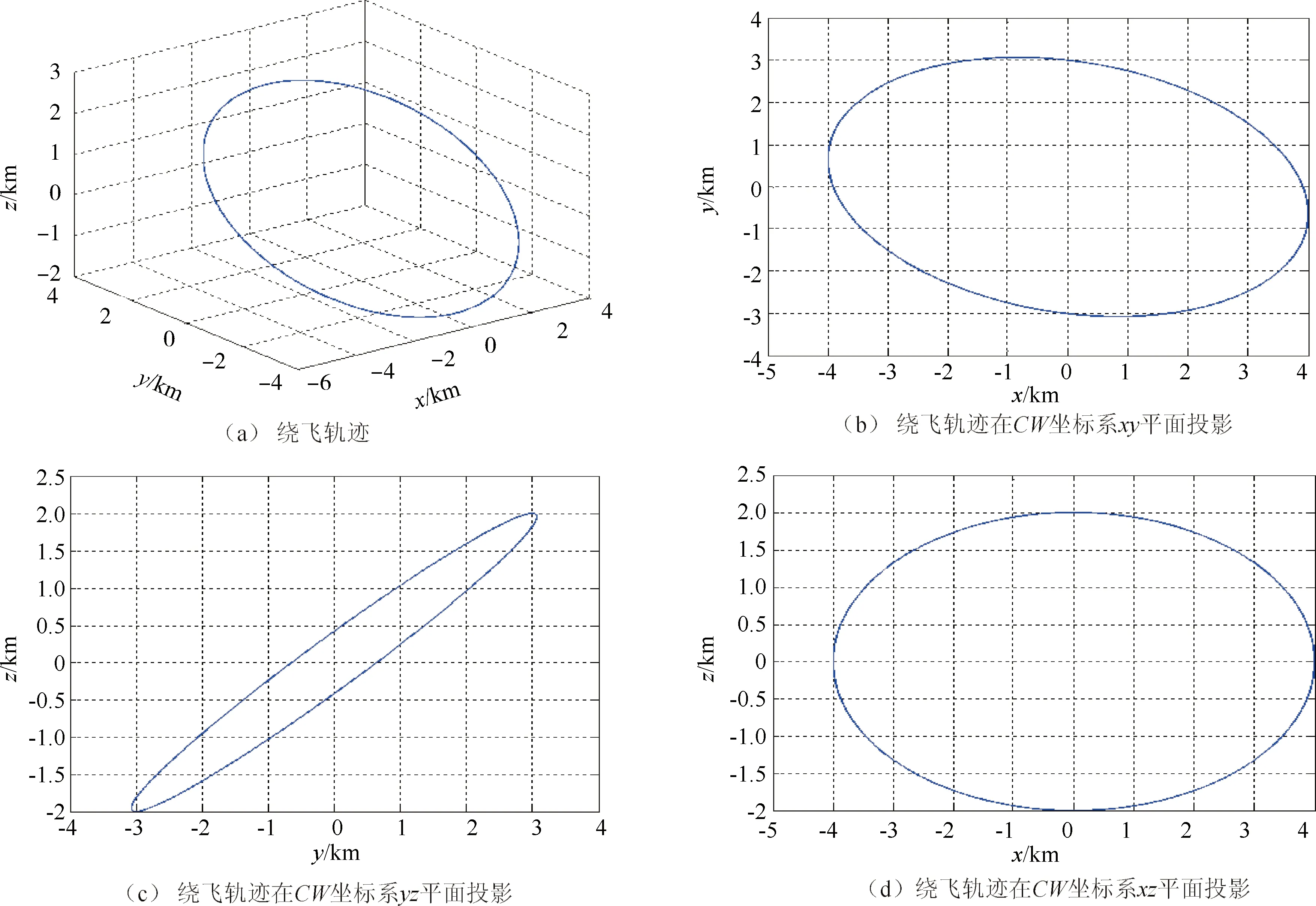
图1 设计的副星轨道1对应的相对主星绕飞轨迹

表2 编队相对绕飞形成与保持控制策略

第4次控制结束时刻为2012年06月01日16时34分 20.266秒。控制后轨道根数为

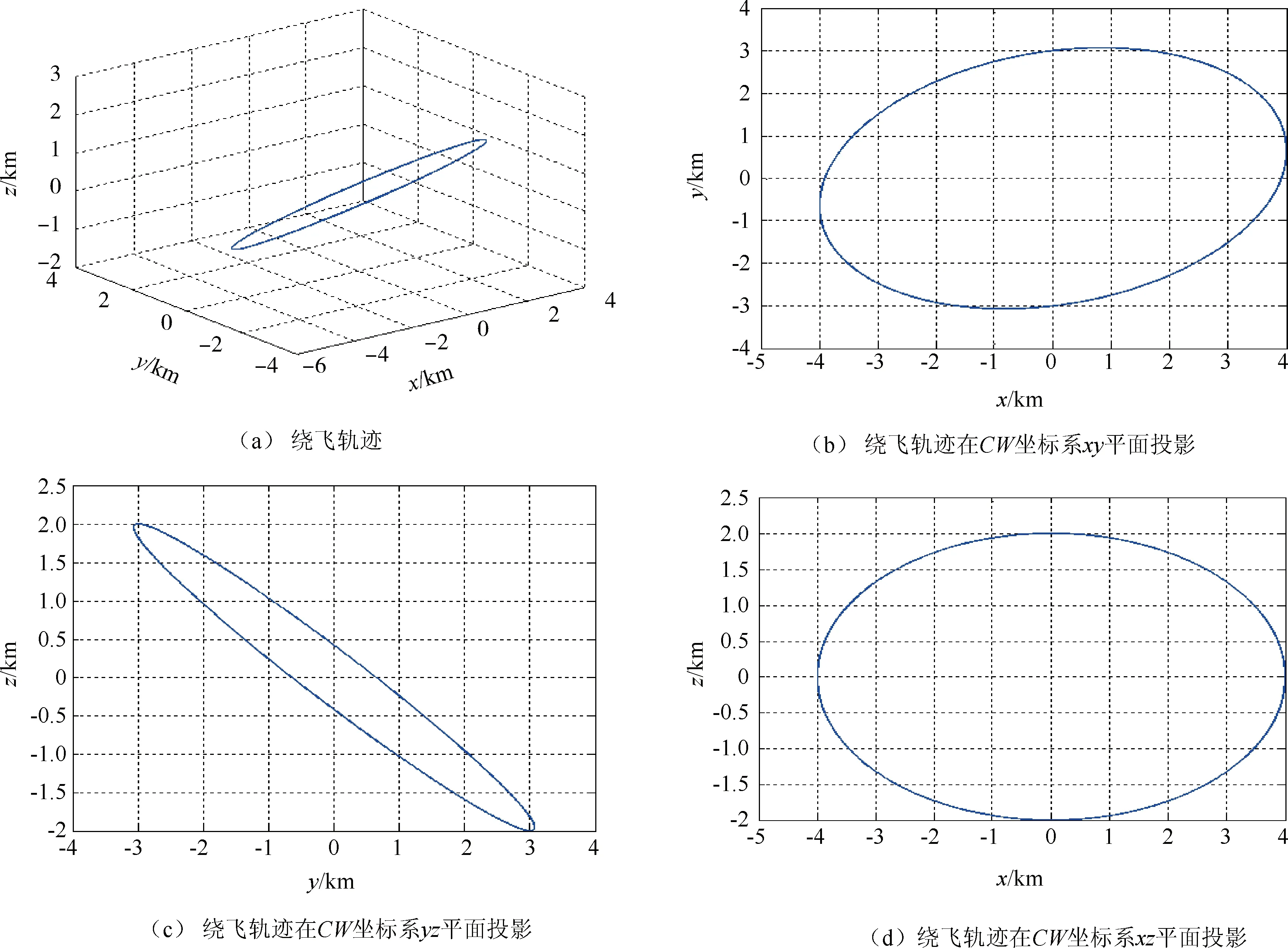
图2 设计的副星轨道2对应的相对主星绕飞轨迹

控制后一个绕飞周期中的最小距离为3477.7m，最大距离为4184.6m，水平绕飞角为34.017°。共进行了4次控制，最大推进时长为295.257s，满足最大推进时长不超过500s的约束。4次控制均安排在北京时间8～23h之间。编队控制过程中最小相对距离为539.1309m，满足控制过程中的最小安全距离为200m的约束。最大距离控制误差为0.69%，最小距离控制误差为0.049%。最后将水平绕飞角控制为34.0175°，一圈内最大瞬时绕飞角为34.026°，一圈内最小瞬时绕飞角为33.934°，可见编队相对绕飞控制策略对水平绕飞角的控制误差仅为0.0175°，且漂移量在0.03°以内，精度很高。将绕飞挠率控制至仅为0.0002，可见该策略对相对绕飞曲面的控制效果非常好，瞬时绕飞平面偏离目标绕飞平面的程度很小。绕飞中心在沿迹方向的分量控制至仅为-5.153m，远小于绕飞中心在沿迹方向的分量相对基线长度的偏离小于5.0%的约束。

表3 控制后长期构形漂移预报结果

由表3可见，使用本文的编队绕飞控制策略进行编队绕飞控制后，绕飞中心、绕飞角、最小距离、最大距离均可良好稳定地保持，控制后编队构形稳定性好,有利于延长保持控制的周期，节约推进剂的消耗。

4 结论

本文提出的卫星编队飞行相对绕飞控制策略，仅需进行切向和法向的控制，控制律不需要改变推力的大小和推力，适用范围广。对一般的单组元冷气推进、双组元推进、电推进等各种推进系统都适用。同时，该控制策略不需要进行卫星的姿态机动，并且对绕飞角、绕飞中心等编队构形参数的控制精度高。此外，使用该控制策略进行控制后，绕飞中心、绕飞角、最小距离、最大距离均可良好稳定地保持，控制后编队构形稳定性好。对于轨道高度在2000km以下、编队基线为5km左右的编队绕飞构形，如果控制执行误差为0.01m，绕飞中心漂移范围限制在600m以内，则控制后编队绕飞构形可保持1年以上，有利于延长保持控制的周期，节约推进剂的消耗。同时，本文还首次实现了对绕飞中心和绕飞挠率的控制。

[1] 陈杰, 周荫清，李春升.分布式SAR小卫星编队轨道设计方法研究[J].中国科学(E辑)信息科学,2004, 34(6):654-662.(Chen Jie, Zhou Yinqing, Li Chunsheng. Study of Orbit Design Methods for Formation Flying with Distributed Small SAR Satellites[J]. Science in China Ser. E Information Sciences, 2004, 34(6): 654-662.)

[2] 张润宁，李洋，李国军.编队飞行干涉SAR卫星系统任务分析与设计[J].航天器工程,2008, 17(5):18-24.(Zhang Running, Li Yang, Li Guojun. Mission Analysis and Design of Formation Flying Interferometric SAR Satellite System[J]. Spacecraft Engineering, 2008, 17(5):18-24.)

[3] Hanspeter Schaub and Kyle T Alfriend .J2 Invariant Relative Orbit for Spacecraft Formations[J]. Celestial Mechanics and Dynamical Astronomy, 2011, 79(2):77-95.

[4] Hanspeter Schaub, Srinivas R Vadali, John L Junkins and Kyle T Alfriend. Spacecraft Formation Flying Control Using Mean Orbit Elements[J]. Journal of the Astronautical Sciences, 2000, 48(1): 69-87.

[5] His-Han Yeh and Andrew Sparks. Geometry and Control of Satellite Formations[C]. Proceedings of the American Control Conference. Chicago, June 2000.

[6] Kyle T Alfriend，Hanspeter Schaub，Dong-Woo Gim. Gravitational Perturbations，Nonlinearity and Circular Orbit Assumption Effects on Formation Flying Control Strategies[R]. Annual AAS Rocky Mountain Guidance and Control Conference. Breckenridge，2000, AAS 00-012.

[7] Simone D Amico and Oliver Montenbruck. Proximity Operations of Formation-Flying Spacecraft Using an Eccentricity/Inclination Vector Separation[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(3): 554-563.

[8] Clohessy W, Wiltshire R. Terminal Guidance System for Satellite Rendezvous[J]. Journal of The Aerospace Sciences,1960, 27(9): 653-658.

[9] Lawden D. Fundamentals of Space Navigation[J]. Journal of the British Interplanetary Society, 1954, 13(2): 87-101.

[10] Srinivas R Vadali. An Analytical Solution for Relative Motion of Satellites[C]. Dynamics and Control of Systems and Structures in Space, 2002, Cranfield Univ, Cranfield, UK,: 309-316.

[11] 杨海峰,尹路明.近地卫星编队构形保持方法[J].航天控制,2010, 28(1):17-20,69.(YANG Haifeng, YIN Luming. A Method for LEO Satellite Formation Keeping[J]. Aerospace Control,2010, 28(1):17-20,69.)

[12] 郭碧波,李立涛,强文义,等.卫星编队飞行相对位置保持的脉冲控制[J].航天控制,2007, 25(2):32-35,91. (Guo Bibo , Li Litao , Qiang Wenyi,et al. Pulse-based Control of Relative Station-keeping about Formation Flying Satellites[J]. Aerospace Control, 2007, 25(2):32-35,91.)

[13] 张保群,宋申民,陈兴林.带时延和拓扑切换的编队卫星鲁棒协同控制[J].宇航学报,2012,33(7):910-919.(Zhang Baoqun, Song Shenmin, Chen Xinglin. Robust Coordinated Control for Formation Flying Satellites with Time Delays and Switching Topologies[J]. Journal of Astronautics, 2012, 33(7):910-919.)

[14] Brower D. Solution of the Problem of Artificial Satellite Theory without Drag[J]. Astronautical Journal, 1959, 64(1274): 378-397.

Relative Fly-Around Control Strategy for Satellite Formation Flying

JIANG Yu1,2LI Hengnian1PAN Ligong1HU Jing1BAOYIN Hexi2

1. State Key Laboratory of Astronautic Dynamics, Xi’an 710043, China 2. School of Aerospace, Tsinghua University, Beijing 100084, China

Arelativeflyaroundcontrolstrategywithsophisticatedperturbationforsatelliteformationflyingispresented.Thecontrolofalong-trackandcross-trackmaneuversisonlyrequiredintheproposedstrategy.Theattitude,thesizeandthedirectionofthethrustdon’tneedtochangewhenthecontrolstrategyisexecuting.Theparametersofformationconfiguration,includingflyaroundangle,flyaroundcenter,flyaroundbaselineandetc,havehighprecisioninthiscontrolstrategy.Thewarpoftheflyaroundangleislessthan0.05degreeaftercontrol,andtheflyaroundtorsionislessthan0.001aftercontrol.Besides,thestabilityofformationconfigurationisfine.Theflyaroundcenter,theflyaroundangle,theflyaroundbaseline,theminimumrelativedistanceandthemaximalrelativedistancecankeepforalongtime.Therefore,thecontrolperiodcanbeextendedandthepropellantcanbeeconomized.Therelativeflyaroundcontrolstrategyrealizesthecontroloftheflyaroundcenterandtheflyaroundtorsionforthefirsttime.

Satelliteformationflying;Flyaroundcurvature;Flyaroundtorsion;Flyaroundcontrol;Relativecontrol;Controlstrategy

2013-10-14

姜 宇(1983-),男，陕西子洲人，硕士研究生，工程师，主要研究方向为航天器编队飞行与星座控制、强不规则天体势场中的探测器运动等；李恒年(1967-)，男，甘肃永昌人，博士，研究员，主要研究方向为卫星动力学与控制等；潘立公(1968-)，男，山西万荣人，硕士，高级工程师，主要研究方向为航天测控总体与调度管理等；胡 静(1983-)，女，陕西子洲人，硕士，助理工程师，主要研究方向为航天器轨道动力学与仿真等；宝音贺西(1972-)，男，内蒙古扎赉特旗人，博士，博士研究生导师，教授，主要研究方向为行星际探测轨道设计、强不规则天体势场中的探测器运动等。

V448.2

A

1006-3242(2014)01-0055-08