直流配网线路供电能力分析

刘自发，李韦姝，韦涛，惠慧

(1.华北电力大学电气与电子工程学院，北京市 102206;2.中国电力科学研究院配电研究所，北京市 100192)

0 引言

随着我国新能源、信息技术、电力电子技术等的发展和经济的迅速增长，用户的用电需求以及对电能质量、供电可靠性、经济性和环保性的要求不断提高，配电网面临着负荷多样化、城市中心供电能力不足、供电走廊紧张、分布式电源接入等问题。

与交流配电网相比，直流配电网具有供电容量大［1-4］、线路损耗小［5-7］、能量传输效率高［8-10］、电能质量好［11-12］、供电可靠性高［13］以及适于可再生能源接入［14-15］等一系列优点。光伏电池及燃料电池发出的是直流电，需要经过DC/AC换流器才能并入交流电网;风力发电发出的是随机波动的交流电，需要经过AC/DC/AC换流器才能并入交流电网。目前许多直流负荷，输入端的AC/DC换流器也是为交流供电而设计，若采用直流供电，则可省略中间的整流或逆变环节，节能降耗，分布式发电并网的控制技术也简单得多［14］。

在线路供电能力的研究中，文献［16-18］以电压降为约束条件，比较了交流配电网中不同电压等级下不同型号导线的供电半径;文献［7，19］以线路最大电流及电压降为约束条件，给出了直流配电网中线路最大传输功率随线路长度的变化趋势。目前国内外对直流配电网供电能力的详细研究较少，还没有考虑到线路功率损耗作为约束条件，本文推导直流配电网中线路分别在允许电压降及线路功率损耗约束下的供电能力计算模型，并通过与交流配电网相应指标的比较，评估直流配电网供电能力较之交流配电网的优劣。

1 供电能力指标及计算模型

通常所说线路的供电能力，是指一定电压的供电线路在满足供电安全和可靠性的情况下，能供多少负荷，能供多远距离，即线路的供电能力指标可用负荷矩与供电距离来表示。

1.1 以电压降作为约束条件时的计算模型

线路压降与输送的负荷、线路长度、电压等级及功率因数密切相关，因此我们可以从计算线路电压降入手，对交流线路、直流单极线路、直流双极线路的供电能力分别进行分析。

1.1.1 交流线路计算模型

对于某一电压等级的供电线路，由于线路存在着阻抗，当有负荷电流通过时，在线路上要产生电压损耗。负荷的分布形式有:集中在线路末端，沿线路均匀分布，沿线路等差级数递增或递减，以及沿线路不规则分布。此处按照极限情况，负荷集中在线路末端计算。电压损耗的计算公式［20］如下:

式中:P为线路输送功率，kW;L为线路长度，km;r0为线路单位长度电阻，Ω/km;x0为线路单位长度电抗，Ω/km;UAC为线路所在电压等级的额定电压，kV;φ为线路的功率因数角。

根据式(2)可以推得线路负荷矩与电压损耗的关系:

式中:I为线路上允许流过的电流，A;β为线路负载率。

将式(4)代入式(3)中，可以得出线路的输送距离与电压损耗的关系为

1.1.2 允许压降约束时直流单极线路计算模型

直流单极送电采用的是直流单极导体回流方式，当电力负荷集中在线路末端时，产生的电压损耗［21］为

式中UDC1为单极直流供电线路的电压，kV。

推得直流单极线路负荷矩与电压损耗的关系为

直流单极线路输送的功率为

则可求出直流单极线路的供电距离与电压损耗的关系为

1.1.3 允许压降约束时直流双极线路计算模型

直流双极送电采用的是中性点两端接地方式，若采用电压为±UDC2的线路供电，当电力负荷集中在线路末端时，产生的电压损耗［21］为

式中UDC2为双极直流供电线路的电压，kV。

推得直流双极线路负荷矩与电压损耗的关系为

直流双极线路输送的功率为

则可求出直流双极线路的供电距离与电压损耗的关系为

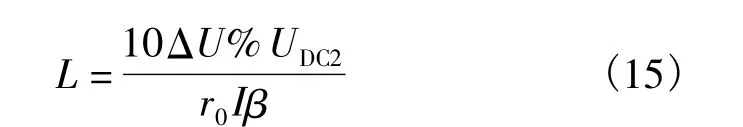
1.2 以线路功率损耗作为约束条件时的计算模型

对于交流供电线路，按照最大允许电压损耗进行计算即可，而直流供电线路，除了在满足电压损耗约束条件外，还需满足线路功率损耗不能过大，其计算模型如下所述。

1.2.1 允许线损约束时直流单极线路计算模型

采用直流单极导体回流方式，当电力负荷集中在线路末端时，在线路上产生的功率损耗［21］为

可得出直流单极线路负荷矩与线损率的关系为

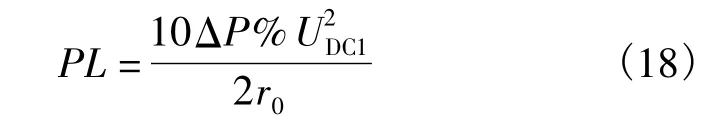
结合式(9)，直流单极线路的供电距离与线损率的关系为

1.2.2 允许线损约束时直流双极线路计算模型

采用中性点两端接地方式，当电力负荷集中在线路末端时，在线路上产生的功率损耗［21］为

则直流双极线路负荷矩与线损率的关系为

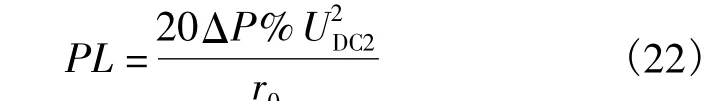
结合式(14)，直流双极线路的供电距离与线损率的关系为

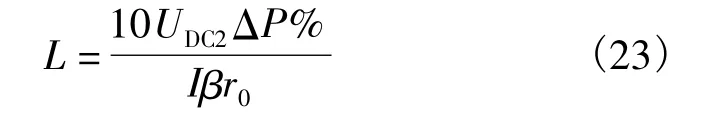
2 供电能力计算

由于目前中压直流配网的电压等级尚未确定，为比较交流线路与直流线路的供电能力，在选择直流系统电压时，须考虑到设备在直流系统中的绝缘水平。在交流系统中，相间绝缘承受的最大工作电压为线电压，而将交流配网改造为直流时，直流电缆允许电压为交流额定电压的峰值［1］。由此，可得出直流电压与交流电压的关系为

根据现有中压交流配网的电压等级，设定4个中压交流电压等级，分别为 10，15，20，25 kV，对应的单极直流电压为 14，21，28，35 kV，双极直流电压为±7，±10.5，±14，±17.5 kV。计算线路在对应电压等级下的负荷矩和供电距离，线路采用几种常用的架空线和电缆，参数值如表1所示。计算时取线路负载率为50%。

表1 常用导线电气参数Tab.1 Electrical parameters of commonly used wires

对于交流线路，根据GB 12325—1990《电能质量供电电压允许偏差》中规定:中压配网三相供电电压允许偏差为额定电压的±7%。线路的功率因数取0.9。

对于直流线路，以电压降落作为约束条件计算时，选择直流系统中所设定电压等级的电压降均为7%。以线路功率损耗作为约束条件计算时，根据经验值，选择功率损耗为3%。

2.1 按照允许电压降的计算结果

根据参数设置、表1的导线参数以及上述公式，可以计算出电力负荷集中在线路末端时，常用导线在满足允许的电压降的条件下，各设定电压等级的负荷矩和供电距离，计算结果如表2～5所示。计算出的直流双极线路负荷矩与供电距离与直流单极线路相等，将计算结果列在一个表中，括号内表示直流双极线路的电压。

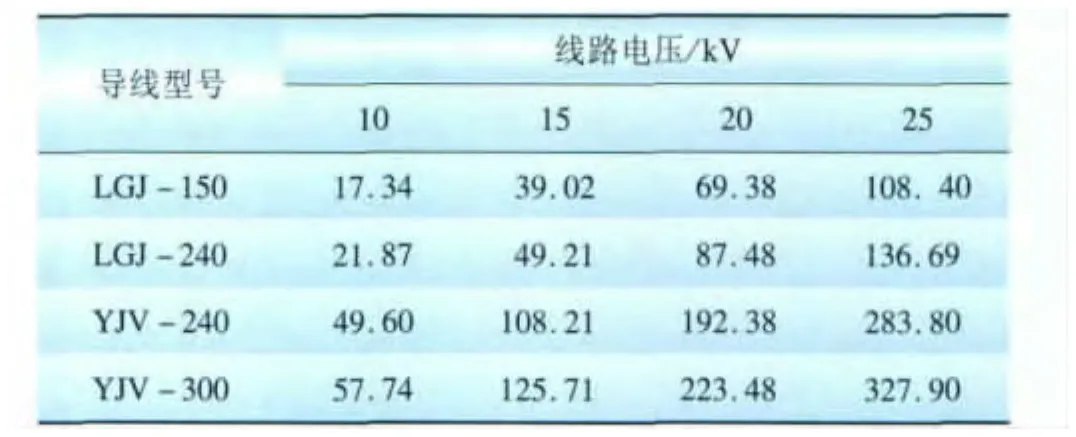
表2 交流线路负荷矩Tab.2 Load moment of AC power lineMW·km

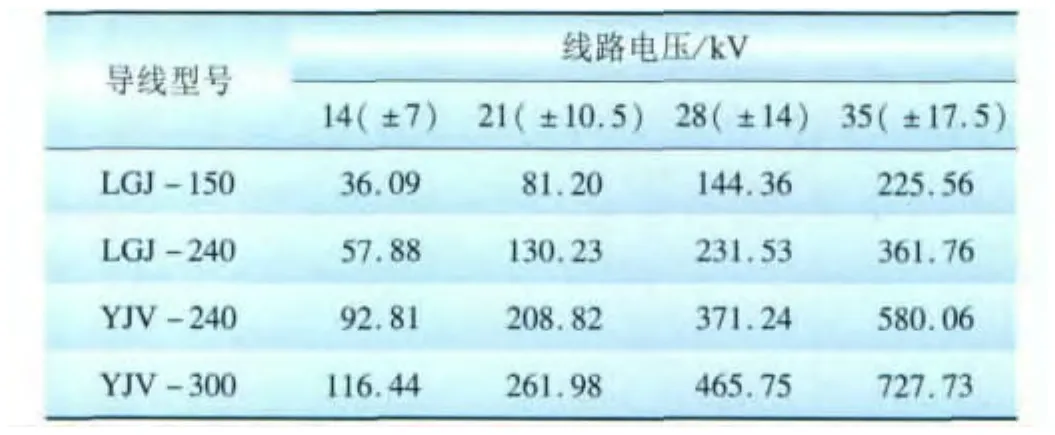
表3 允许压降约束时直流单(双)极线路负荷矩Tab.3 Load moment of DC monopole(bipolar)power line with allowed voltage drop constraintMW·km

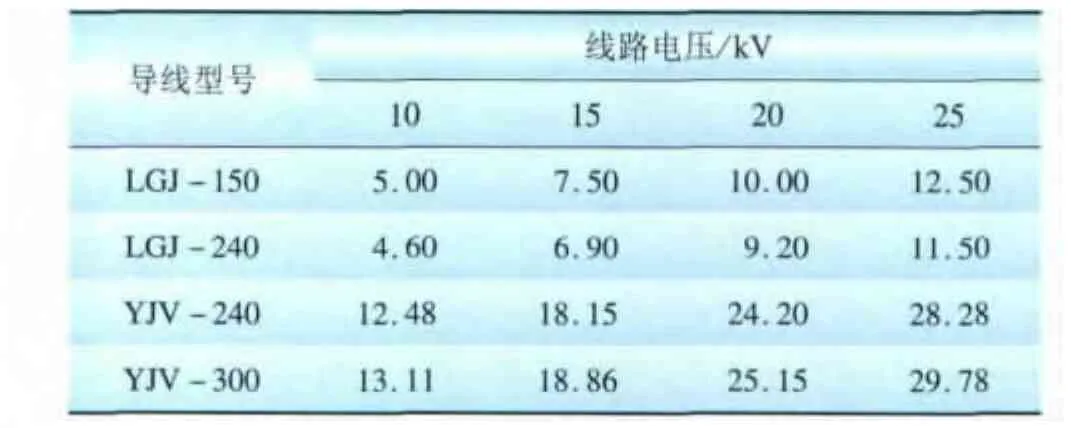
表4 交流线路供电距离Tab.4 Supply distance of AC power line km

2.2 按照允许功率损耗的计算结果

根据参数设置、表1的导线参数及上述公式，可以计算出当电力负荷集中在线路末端时，直流线路在满足允许的功率损耗条件下，分别在4个电压等级下的负荷矩和供电距离，如表6～7所示。

表5 允许压降约束时直流单(双)极线路供电距离Tab.5 Supply distance of DC monopole(bipolar)power line with allowed voltage drop constraint km

表6 允许线损约束时直流单(双)极线路负荷矩Tab.6 Load moment of DC monopole(bipolar)power line with allowed power loss constraint MW·km

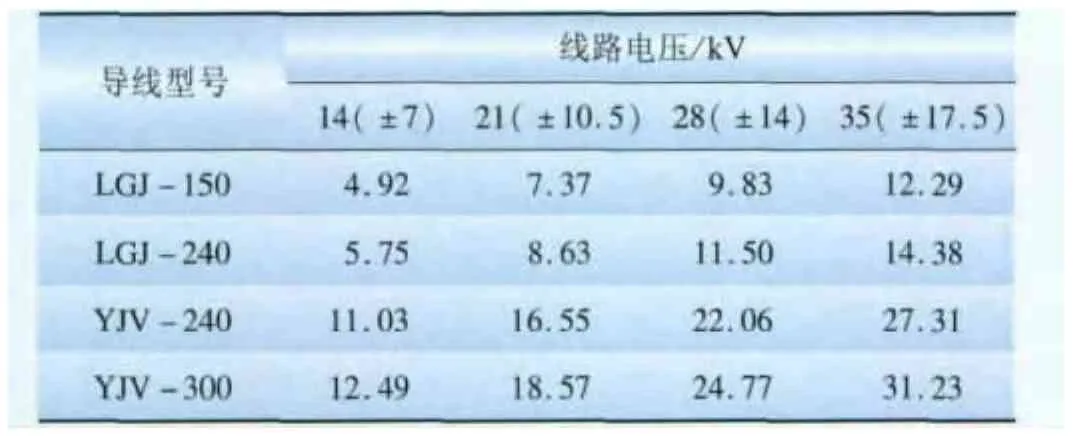
表7 允许线损约束时直流单(双)极线路供电距离Tab.7 Supply distance of DC monopole(bipolar)power line with allowed power loss constraint km

2.3 约束条件的选取

同时考虑到电压降约束以及功率损耗约束，将以电压降落为约束条件的线路供电能力计算结果，与以功率损耗为约束条件的线路供电能力计算结果相比，可以看出，当满足功率损耗为3%时，直流线路的负荷矩与最大供电距离比满足电压降为7%时的负荷矩与最大供电距离小，直流系统中线路约束对功率损耗较敏感，即在计算线路供电能力时，功率损耗约束比电压降约束更能起到约束作用。满足允许的功率损耗，则能保证电压降落不会越限。

究其原因，主要是由于在直流系统中，只有有功功率与线路的电阻，没有无功功率及电抗，使得直流系统中，线损率与电压降落相等，对比式(7)和(17)，式(12)和(21)可证明这一点。当满足电压降落为7%时，与功率损耗为7%时计算出来的负荷矩与最大供电距离相等，当满足功率损耗为3%时，此时线路上的电压降落也为3%。因此，为保证系统运行的经济性，应当选择允许功率损耗作为直流系统供电能力计算的有效约束条件。

3 交直流系统供电能力对比

分析计算结果，各个对应电压下交直流系统负荷矩变化趋势相同，因此，本文选择架空线LGJ-240和电缆YJV-300，在各自有效约束条件下，做出电力负荷集中在线路末端时，交流系统与直流系统中线路的负荷矩对比图，如图1、2所示。

图1 LGJ-240负荷矩对比Fig.1 Load moment comparison for LGJ-240

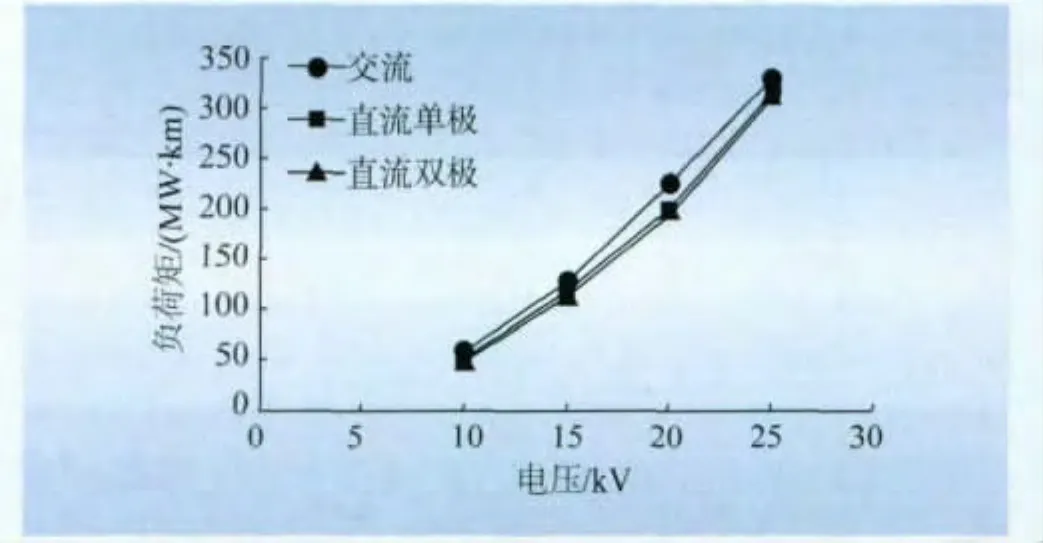
图2 YJV-300负荷矩对比Fig.2 Load moment comparison for YJV-300

从图1～2中可以看出，在相同绝缘水平下，架空线LGJ-240的直流供电能力较交流略大，电缆YJV-300的直流供电能力较交流略小。主要原因是LGJ型架空线的电抗比电缆电抗大，在交流系统中的压降损失大，计算供电能力时，交流线路是允许电压降起有效约束作用，因此LGJ-240的直流供电能力略大于交流供电能力，而YJV-300的直流供电能力较交流略小。

对于负荷的另外几种典型分布形式:沿线均匀分布，沿线路等差级数递增或递减分布，中间大两端小分布，根据文献［22］中的表1～23分散负荷与末端集中负荷间的系数关系，交流线路以允许电压偏差作为有效约束条件，负荷呈均匀分布、递增分布、递减分布、中间大两端小分布时引起的电压损耗分别为负荷集中在末端时引起电压损耗的0.5、0.67、0.33、0.5倍;直流线路以允许线损率作为有效约束条件，负荷呈均匀分布、递增分布、递减分布、中间大两端小分布时引起的功率损耗分别为负荷集中在末端时引起功率损耗的 0.33、0.53、0.2、0.38倍，可得出架空线LGJ-240和电缆YJV-300在不同负荷分布形式下的负荷矩，如表8所示。线路电压仍设定为相同绝缘水平，直流单双极负荷矩计算结果相等，合并列出。

表8 典型负荷分布形式下线路负荷矩Tab.8 Load moment under typical load distribution patterns MW·km

通过表8的对比可看出，当负荷呈现4种典型分布时，在相同绝缘水平下，均有直流线路的供电能力大于交流线路。

负荷集中在线路末端时，由负荷矩与供电距离的计算公式可知，直流线路负荷矩与线路电压的平方成正比，供电距离与线路电压成正比，若直流线路电压等于交流线路电压，计算出直流线路的供电能力小于交流线路。根据文献［21］，直流的绝缘耐受能力比交流强，对于架空线路，直流极对地电压可以提高至交流相电压的1.5～2.5倍，对于电缆线路，直流极对地电压可以提高至交流相电压的3～5倍。

若将电缆线路的直流电压提高至交流相电压的3倍，对应10，20 kV交流线路电压，直流单极线路电压为17，34 kV，直流双极线路电压为±8.5，±17 kV。则交直流电缆线路的负荷矩与供电距离计算结果如表9所示。计算出的直流双极线路的负荷矩与供电距离与直流单极线路相等，将结果列在一起。由表9可知，当电缆线路直流电压提高至交流相电压的3倍时，在直流中的供电能力大于交流。

表9 电缆线路直流电压为交流相电压3倍时的供电能力计算结果Tab.9 Results of power supply capability when DC voltage equals to 3 times AC phase voltage of cable line

对于不同型号线路，计算出当线路的直流供电能力与交流供电能力相当时，直流线路的临界电压值，如表10所示，UAC表示交流线路线电压，括号内表示直流双极线路电压。当直流电压大于此临界值时，直流线路供电能力大于交流线路。

表10 交直流供电能力相当时直流电压临界值Tab.10 Threshold of DC voltage when power supply capability of DC equals that of AC

4 结论

本文通过对交流供电线路供电能力的分析，推导出直流供电线路的供电能力计算模型，选择常用的架空线路LGJ-150、LGJ-240及电缆线路YJV-240、YJV-300，设定允许电压降为7%，允许功率损耗为3%，在4个线路电压下分别进行了交直流线路负荷矩及供电距离的比较，得出如下结论:

(1)根据设定条件，计算供电能力时，交流线路中是允许电压偏差起有效约束作用，而直流线路中是允许功率损耗起有效约束作用。

(2)在设定的条件下，对于LGJ-240及YJV-300在几种典型负荷分布形式下进行了供电能力比较。负荷集中在线路末端时，在相同电压下，直流的供电能力小于交流。在相同绝缘水平下，LGJ--240的直流供电能力较交流略大，YJV-300的直流供电能力较交流略小。由于直流的绝缘耐受能力比交流强，当直流线路电压高于对应临界值时，直流线路的供电能力大于交流线路。

［1］江道灼，郑欢.直流配电网研究现状与展望［J］.电力系统自动化，2012，36(8):98-104.

［2］谭逢时.未来直流配电网建设初探［J］.科技资讯，2011(23):110-112.

［3］Hammerstrom D J.AC versus DC distribution systems-did we get it right［C］//Proceedings of IEEE Power Engineering Society General Meeting，2007，Tampa，FL，USA:1-5.

［4］Starke M，Li F X，Tolbert L M，et al.AC vs.DC distribution:maximum transfer capability［C］//Proceedings of IEEE Power and Energy Society GeneralMeeting-Conversion and Delivery of Electrical Energy in the 21st Century，2008，Pittsburgh，PA，USA:1-6.

［5］Starke M R，Olbert L M，Ozpinect B.AC vs.DC distribution:a loss comparison［C］//Proceedings ofIEEE/PES Transmission and Distribution Conference and Exposition，April 21-24，2008，Chicago，IL，USA:1-7.

［6］Amin M，Arafat Y，Lundberg S，et al.Low voltage DC distribution system compared with 230 V AC［C］//Proceedings of Electrical Power and Energy Conference(EPEC)，2011，Winnipeg，MB:340-345.

［7］Ssnnino A，Postiglione G，Bollen M H J.Feasibility of a DC network for commercialfacilities［J］.IEEE Transactionson Industry Applications，2003，39(5):1499-1507.

［8］Pang H，Lo E，Pong B.DC electrical distribution systems in buildings［C］//Proceedings of the 2nd International Conference on Power Electronics Systems and Applications，2006，Hong Kong，China:115-119.

［9］Nilsson D，Sannino A.Efficiency analysis of low-and-mediumvoltage DC distribution systems［C］//Proceedings of IEEE Power Engineering Society General Meeting，2004，Denver，CO，USA:1-7.

［10］Dastgeer F，Kalam A.Efficiency comparison of DC and AC distribution systems for distributed generation［C］//Proceedings of Australasian Universities Power EngineeringConference，2009，Adelaide，SA，Australia:1-5.

［11］Musolino V，Piegari L，Tironi E，et al.Simulations and field test results for potential applications of LVDC distribution network to reduce flicker effect［C］//Proceedings of 14th International Conference on Harmonics and Quality of Power，2010，Bergamo，Italy:1-6.

［12］汤广福.基于电压源换流器的高压直流输电技术［M］.北京:中国电力出版社，2009.

［13］Sithmolada V，Sauer P W.Facility-level DC vs.typical AC distribution for data centers［C］//Proceedings of 2010 IEEE Region 10 Conference，2010，Fukuoka，Japan:2102-2107.

［14］Wang F，Pei Y Q，Boroyevich D，et al.AC vs.DC distribution for off-shore power delivery［C］//Proceedings of IEEE 34th Annual Conference，2008，Orlando，FL，USA:2113-2118.

［15］胡航海，李敬如，杨卫红，等.柔性直流输电技术的发展与展望［J］.电力建设，2011，32(5):62-66.

［16］李金芳，刘宗岐，张建华，等.中压配电电压等级选择研究［J］.现代电力，2009，26(4):51-55.

［17］马勇飞，王沧海，王献敏，等.浅析配电网供电半径与最大供电负荷的关系［J］.青海电力，2011，30(1):1-3.

［18］朱娅.20 kV配电网的技术性研究［D］.成都:西南交通大学，2012.

［19］Agustoni A，Borioli E，Brenna M，et al.LV DC distribution network with distributed energy resources:Analysis of possible structures［C］//Proceedings of 18th International Conference and Exhibition on Electricity Distribution，2005，Turin，Italy:1-5.

［20］陈珩.电力系统稳态分析［M］.北京:中国电力出版社，2007.

［21］赵畹君.高压直流输电工程技术［M］.北京:中国电力出版社，2011.

［22］方大千.输配电速查速算手册［M］.北京:中国水利水电出版社，2004.