多重赋权模糊综合评价在采场结构参数优化中的应用
2014-08-08郭奇峰任奋华
彭 超 郭奇峰 冀 东 赵 亮 任奋华
(1.北京科技大学土木与环境工程学院,北京 100083;2.金属矿山高效开采与安全教育部重点实验室,北京 100083)
多重赋权模糊综合评价在采场结构参数优化中的应用
彭 超1,2郭奇峰1,2冀 东1,2赵 亮1,2任奋华1,2
(1.北京科技大学土木与环境工程学院,北京 100083;2.金属矿山高效开采与安全教育部重点实验室,北京 100083)
房柱交替式上向分层充填法是三山岛金矿深部采用的主要采矿方法,国内采用该方法的矿山所选取的结构参数大小不一,因此依靠工程经验类比难以得出适合矿山的采场参数。针对这个问题,结合三山岛金矿深部高应力、高岩爆倾向性的特点,通过数值模拟得到不同结构参数条件下采场一步采与二步采过程中盘区顶板沉降和采场内的位移,综合考虑相对生产能力、综合效率、设备匹配度、施工难度等因素,建立了采场参数的模糊综合评价模型。通过合理确定评价指标的隶属度函数,以及运用变异系数法、模糊判据法和熵值法的多重赋权优化确定各评价指标的权重,对列出的5种方案进行综合评价,确定了符合矿山实际条件的最优采场参数,从而保证了矿山的安全生产和经济效益。
综合评价 采场参数优化 隶属度 权重
山东黄金集团三山岛金矿是我国第一个进行海底采矿的硬岩矿山,其矿体位于海床下数十米至数百米范围内,是完全意义上的海底开采。为了满足生产能力和安全性的要求,矿山深部采用房柱交替式上向分层充填采矿法,该方法开采贫化率和损失率相对较低,回采安全性很好,可以很好地适应深部开采面临的高应力和高岩爆倾向性问题[1]。目前国内采用该采矿方法的矿山所采用的结构参数大小不一,矿房、矿柱的宽度6~15 m不等,针对三山岛金矿深部高应力、高岩爆倾向性以及开采规模和开采难度增加的特点[2],单纯依靠工程经验类比的方法已经不再适用。
本研究建立采场参数的模糊综合评价模型,通过数值模拟确定优化指标值,运用变异系数法、模糊判据法和熵值法的多重赋权优化确定各评价指标的权重,利用模糊评价方法进行采场结构参数的优化研究,最终确定符合矿山实际条件的最优采场参数,对实现大产能和高效经济开采,满足生产安全要求具有重要意义。
1 多重赋权模糊综合评价模型
1.1 模糊评判定义
模糊评判是指在模糊环境中对受多因素影响的事物做出全面评价的一种多因素决策方法[3-4]。进行模糊评判首先要定义2个集合:设
U为由m个评判因素组成的集合,称为因素集;设
V为由n个决策评语组成的集合,称为评判集。
1.2 隶属度矩阵的确定
如果对每一个ui单独做一个模糊评判,则得到因素ui的单因素评判集合为
对m个影响因素的评判就构成了总的因素评判矩阵R,R=(rij)m×n表示因素集U与评判集V之间的模糊关系,其中表rij示第i个影响因素ui对该事物的决策评语vj的隶属度。根据评判因素性质的不同,隶属度矩阵分为以下两种[5]。
(1)定量指标隶属度矩阵。定量指标隶属度矩阵采用隶属函数法确定,将定量指标构建成目标特征值矩阵。对数值越大越优指标,采用式(1)进行计算;对数值越小越优指标,采用式(2)进行计算:
(1)
(2)
式中,yij为第i个指标属于j个评判类别的标准值;rij为相对隶属矩阵的因素。从而得到定量指标隶属度矩阵
(3)
(2)定性指标相对隶属度矩阵。定性指标的相对隶属度采用相对二元比较法进行规格化,依据如下原则确定排序标度:若Rk比Rl重要,令rkl=1,rlk=0;若Rk与Rl同样重要,令rkl=0.5,rlk=0.5;若Rl比Rk重要,令rkl=0,rlk=1;其中k=1,2,…,m,l=1,2,…,n。建立非定量特征向量矩阵
(4)
将定性特征向量矩阵各行之和,按照由大到小排列,得到各指标的重要性排序,数值相同,则排序相同。根据重要性排序,按照表1所示语气算子与定量标度表[6],建立定性指标的相对隶属度矩阵。将定量指标隶属度矩阵R1与定性指标隶属度矩阵R2合并,得到优化指标的综合隶属度矩阵R。

表1 语气算子与定量标度相对隶属度关系Table 1 Relative membership between mood operator and quantitative scale
1.3 权重向量的确定
由于各因素ui在决策中起的作用大小不同,权重不同,因而评判也就不同。所以定义一个模糊集合
A称为U的因素重要度的权重向量,ai表示第i个影响因素ui的权重,且它们满足归一化条件
本研究采用变异系数法、模糊判据法和熵值法计算各优化指标的权重值[7-9],建立优化权重向量,对各赋权法确定的优化指标相对重要性排序进行一致性评价[10],在此基础上采用加权平均的方法计算三种赋权方案的平均权重为最终组合权重向量。
1.4 模糊综合评判
当权重向量A和隶属度矩阵R为已知时,可以得到由三元体(U,V,R)组成的模糊综合评判模型。可做模糊变换进行综合评价:
其中,
B即为评判集V上的等级模糊子矩阵,得到B后可根据最大隶属度原则进行分类。
2 基于数值模拟的优化指标隶属度研究
随着计算机技术的发展,以FLAC3D为代表三维有限元分析软件在矿山中的应用越来越广泛和深入,可用于模拟采场稳定性问题,模拟开采过程中的应力、位移情况,为解决开采过程的设计和施工提供了十分可靠的定量数据和依据。
2.1 数值模型的建立
以三山岛金矿-555 m水平为模拟对象,机械化盘区式开采沿矿体走向划分8个连续采场,采场垂直矿体走向布置,盘区实际埋深为-510~-555 m。FLAC3D数值模型尺寸选取X(垂直矿体走向方向)方向400 m,Y(沿矿体走向方向)方向300 m,Z(垂直方向)方向200 m。模型顶部实际埋深-430 m,底部埋深-630 m。其中矿体厚度取30 m,倾角45°,盘区高度45 m。FLAC3D数值计算模型如图1所示,图1中包含矿体、充填体、上盘、下盘、断层5种介质。一步采二步采的回采顺序如图2所示。

图1 数值模型图
图2 一步采二步采回采顺序示意
为对三山岛金矿深部房柱交替式上向分层充填开采过程中的一步采与二步采的采场宽度布置进行优化,通过工程类比设计5个一步采宽和二步采宽搭配方案如表2所示,针对各方案分别建立FLAC3D模型进行模拟开采,构建采场结构参数的加权多重赋权优化模型,提取开采过程中盘区顶板沉降(最终开挖边界顶板)、上盘竖向位移以及采场内的Z向位移、X向位移、X向应力、Y向位移和Y向应力作为优化的定量指标,参考综合效率、相对生产能力、设备匹配度、施工难度等定性指标进行优化选择。
表2 5个拟定搭配方案

Table 2 The parameters of five schemes m
采用房柱交替式上向分层充填采矿法,机械化盘区布置,相邻的一步矿房与二步矿房交替上升开采。数值模拟在盘区内连续布置8个矿房,根据开挖和充填的交替,将各方案分6步进行开挖,每一步的开采充填状态如下。
步骤1:2、4、6、8采场回采高度9.5 m,接顶充填,1、3、5、7采场回采高度0 m。
步骤2:2、4、6、8采场回采高度9.5 m,接顶充填,1、3、5、7采场回采高度17.5 m,接顶充填。
步骤3:2、4、6、8采场回采高度27 m,接顶充填,1、3、5、7采场回采高度17.5 m,接顶充填。
步骤4:2、4、6、8采场回采高度27 m,接顶充填,1、3、5、7采场回采高度35 m,接顶充填。
步骤5:2、4、6、8采场回采高度42 m,接顶充填,1、3、5、7采场回采高度35 m,接顶充填。
步骤6:2、4、6、8采场回采高度42 m,接顶充填,1、3、5、7采场回采高度42 m,接顶充填。
根据三山岛金矿深部矿岩物理力学试验结果,参考《GB50218—92 工程岩体分级标准》和《岩土工程勘察规范》和三山岛金矿深部开采工程地质条件对岩体工程力学参数强度系数折减,结合工程经验综合选取数值计算模型中上盘围岩、下盘围岩、矿体、断层的岩体力学参数如表3所示。

表3 岩体力学参数Table 3 The mechanical parameters of rock mass
在深部采场结构参数优化模拟计算过程中,采场埋深在-500 m以下,故依据地应力测量结果和三山岛金矿深部构造赋存状态,将实测地应力按梯度施加到模型边界,模型底面限制Z方向位移,垂直X轴的两个表面限制X方向位移,垂直Y轴的两个表面限制Z方向位移。
2.2 采场结构参数优化指标及其隶属度的确定
根据采场结构参数优化方案的设计,采用FLAC3D数值模拟软件对5个采场结构参数方案进行开采模拟,利用FLAC3D内嵌的FISH语言提取各个方案6个开挖阶段的顶板最大沉降量、上盘最大竖向位移、采场最大竖向位移、采场最大X向位移、采场最大X向应力、采场最大Y向位移、采场最大Y向应力指标。并结合综合效率、相对生产能力、设备匹配度和施工难度为优化的4项非定量指标,采场结构参数加权多重赋权优化的指标如表4所示。
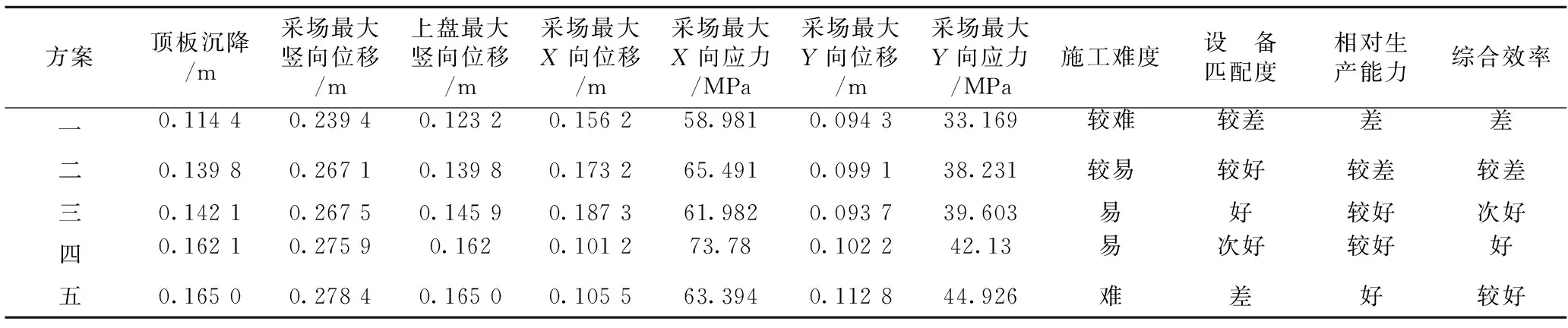
表4 采场结构参数优化评价指标Table 4 Index value for optimization of stope structural parameters
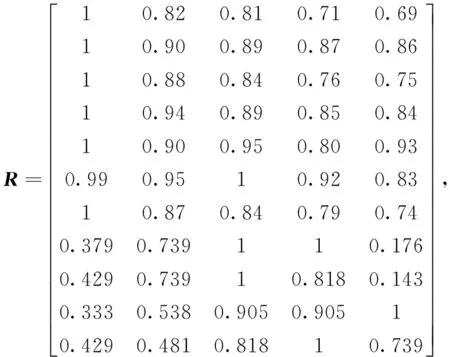
根据表4内容,定量评价指标的相对隶属度矩阵为
根据表1确定各非定量评价指标的相对隶属度向量分别为
综上所述,所有定量指标与非定量指标的综合隶属矩阵为
3 基于加权判别的多重赋权优化
(1)变异系数法赋权。变异系数法赋权的原则是使各指标权重离散度最大化,对于数值差异小的指标赋予较小权重,数值差异大的指标赋予较大权重。根据上述综合隶属矩阵,计算矩阵各行向量的均值与方差:
(5)
(6)
通过下式计算各指标变异系数:
(7)
获取变异系数矩阵为
A'1=(0.096 52,0.086 07,0.083 18,0.089 69,
0.099 23,0.109 66,0.081 27,0.389 66,
0.399 16,0.255 13,0.245 60).
将变异系数矩阵作归一化处理,则变异系数法赋权的各指标权重如下:
A1=(0.049 876,0.044 476,0.042 983,
0.046 347,0.051 277,0.056 665,0.041 998,
0.201 356,0.206 264,0.131 838,0.126 914).
(2)模糊判据法赋权。根据综合隶属矩阵,计算每项指标的权重:
(8)
获取模糊判据权重矩阵为
A'2=(0.097,0.048,0.077,0.048,0.042,
0.031,0.076,0.1706,0.1871,0.1319,0.1533).
将权重矩阵作归一化处理,则模糊判据法赋权的各指标权重如下:
A2=(0.091 345,0.045 201,0.072 511,
0.045 201,0.039 551,0.029 192,0.071 569,
0.160 655,0.176 194,0.134 211,0.144 363).
(3)熵值法赋权。熵值法是以无序度为衡量指标,其赋权原则是值越大,无序度越高,赋权越小;反之值越小,无序度越小,赋权越大[11]。获取各指标熵值hi后,计算每项指标的权重值:
(9)
获取熵值法权重矩阵为
A'3=(0.546 313,0.513 945,0.532 746,
0.514 095,0.510 512,0.504 257,0.532 101,
0.623 797,0.634 735,0.580 469,0.592 180).
将权重矩阵作归一化处理,则熵值法赋权的各指标权重
A3=(0.089 778,0.084 459,0.087 549,
0.084 484,0.083 895,0.082 867,0.087 443,
0.102 511,0.104 309,0.095 391,0.097 316).
将各赋权方案确定的指标权重进行排序,按权重值由小到达的顺序排序,排序号为1至11的整数。排序后可获取3个赋权方案的组合排序向量均为[7 3 6 4 2 1 5 19 11 8 9]。由此可见3种赋权方法确定的各指标权重之间的相对重要性保持完全一致。因此,为减小单一赋权方法的偶然性,可采用加权平均的方法增加赋权的可靠性,进而获取优化指标的最佳权重向量。
加权平均计算后获取的各优化指标权重向量
A=(0.081 603,0.063 535,0.072 529,
0.063 552,0.062 692,0.062 501,0.072 125,
0.124 820,0.135 148,0.100 948,0.113 433).
根据评价因素隶属度矩阵R和指标的总权重向量A,可以确定5个采场结构参数搭配方案的综合评价结果B=AR=[0.665 477 0.727 196 0.866 88 0.827 150 0.608 348]。
通过多重赋权优化及最大隶属度原则可知,5个方案的优选顺序为4、3、1、2、5。优化结果说明三山岛金矿深部进行房柱交替式采矿的一步采二步采采场宽度均应优先采用10 m宽,采场长度为矿体厚度。
4 结 语
(1)通过数值模拟确定优化指标值,综合考虑相对生产能力、综合效率、设备匹配度、施工难度等因素,构建了比较全面的采场参数优化评价体系。利用变异系数法、模糊判别法和熵值法计算优化指标的组合权重,确定3个组合权重向量一致性后,采用加权平均的计算方法计算权重值,从而确保了各评价因素权重分配科学合理。
(2)采用定量与定性的相结合方法,根据隶属函数法和二元对比优先关系法确定定量和定性指标的隶属矩阵,运用多重赋权优化及最大隶属度原则对深部采场结构参数进行优化研究,使得模糊综合评价结果更加可靠。
(3)依据工程类比,设计5种一步采宽和二步采宽搭配方案,经过计算得到5个采场结构参数搭配方案的综合评价结果。通过最大隶属度原则可知最优采场结构为方案三,即一步采宽和二步采宽均为10 m,矿体厚度作为采场长度。经生产验证,该方案生产成本低,是一种安全高效经济的回采方案。通过采场参数的优化,实现了矿山的大产能和高效开采,从而保证了矿山的安全生产和经济效益。
[1] 蔡美峰.金属矿山采矿设计优化与地压控制:理论与实践[M].北京:科学出版社,2001. Cai Meifeng.Optimization of Mining Design and Control of Ground Pressure in Metal mines:Theory and Practice [M].Beijing:Science Press,2001.
[2] 何满潮,钱七虎.深部岩体力学基础[M].北京:科学出版社,2010. He Manchao,Qian Qihu.The Basis of Deep Rock Mechanics[M].Beijing:Science Press,2010.
[3] 李安贵,张志宏,段凤英.模糊数学及其应用[M].北京:北京科技大学出版社,1993. Li Angui,Zhang Zhihong,Duan Fengying.Fuzzy Mathematics and Applications[M].Beijing:Beijing University of Science & Technology Press,1993.
[4] 王新民,赵 彬,张钦礼.基于层次分析和模糊数学的采矿方法选择[J].中南大学学报:自然科学版,2008(5):875-880. Wang Xinmin,Zhao Bin,Zhang Qinli.Mining method choice based on AHP and fuzzy mathematics[J].Journal of Central South University:Nature Science Edition,2008(5):875-880.
[5] 史太禄,任凤玉,李文增,等.模糊数学在采矿方法优选中的应用[J].金属矿山,2007(11):29-31. Shi Tailu,Ren Fengyu,Li Wenzeng,et al.Application of fuzzy mathematics in optimal choice of mining method[J].Metal Mine,2007(11):29-31.
[6] 姚银佩,李夕兵,赵国彦,等.新城金矿二步矿房采矿方法优选研究[J].矿业研究与开发,2010(5):6-8. Yao Yinpei,Li Xibing,Zhao Guoyan,et al.Optimization of mining method for the second-step chamber in Xincheng Gold Mine[J].Mining Research and Development,2010(5):6-8.
[7] 刘爱华,苏 龙,朱旭波,等.基于距离判别分析与模糊数学的岩体质量评判法[J].采矿与安全工程学报,2011(3):462-467. Liu Aihua,Su Long,Zhu Xubo,et al.Rock quality evaluation based on distance discriminant analysis and fuzzy mathematical method[J].Journal of Mining & Safety Engineering,2011(3):462-467.
[8] 罗一忠,吴爱祥,胡国斌,等.采场人-机-环境系统可靠性模糊综合评价[J].中南大学学报:自然科学版,2006,37(4):804-809. Luo Yizhong,Wu Aixiang,Hu Guobin,et al.Reliability fuzzy comprehensive evaluation of man-machine-environment system in stope[J].Journal of Central South University:Nature Science Edition,2006,37(4):804?809.
[9] 闫文周,顾连胜.熵权决策法在工程评标中的应用[J].西安建筑科技大学学报:自然科学版,2004,36(1):98-100. Yan Wenzhou,Gu Liansheng.Application of the method of entropy proportion in the engineering mark[J].Journal of Xi'an University of Architecture & Technology:Nature Science Edition,2004,36(1):98-100.
[10] 匡乐红,徐林荣,刘宝琛.组合赋权法确定地质灾害危险性评价指标权重[J].地下空间与工程学报,2006(6):1063-1067. Kuang Lehong,Xu Linrong,Liu Baochen.A combination weighting method for determining the index weight in geological hazard risk assessment[J].Chinese Journal of Underground Space and Engineering,2006(6):1063-1067.
[11] 魏新江,邓志秋,魏 纲,等.可拓评价方法和熵值法相结合的基坑安全评价[J].岩土工程学报,2008(S1):672-676. Wei Xinjiang,Deng Zhiqiu,Wei Gang,et al.Safety evaluation of foundation pits by extension assessment method combined with entropy law[J].Chinese Journal of Geotechnical Engineering,2008(S1):672-676.
(责任编辑 石海林)
Application of Fuzzy Comprehensive Analysis Based on Multiple Weights to Optimization of Stope Structure Parameters
Peng Chao1,2Guo Qifeng1,2Ji Dong1,2Zhao Liang1,2Ren Fenhua1,2
(1.SchoolofCivilandEnvironmentalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China;2.TheKeyLaboratoryofHigh-efficientMiningandSafetyofMetalMines,Beijing100083,China)
Alternate room-pillar mining method with ascending backfill is the main one mostly used in deep mining of Sanshandao Gold Mine.In mining practice of the metal mines,mines that adopted this method at domestic usually selected different structural parameters,and therefore,it is difficult to draw suitable parameters relying only on analogy or engineering experience.Aiming at those problems and combining with high stress and rock burst possibility in Sanshandao gold mine,the displacement and roof settlement of the middle section in one-step and two-step mining process under different structural parameters are obtained by numerical simulation.Combined with comprehensive efficiency,relative productivity,equipment matching degree and construction difficulties,the model of fuzzy comprehensive analysis is established.Through scientifically determining the membership function and establishing the weight of each factor by variation coefficient method,fuzzy criteria method and entropy method,five schemes listed are evaluated.Then,the optimal stope parameters for the practical mine are selected so as to ensure safety production and better economic profit as well.
Comprehensive analysis,Optimization of stope structure parameters,Membership degree,Weight vectors
2013-12-02
国家自然科学基金项目(编号:51034001)。
彭 超(1985—),男,博士研究生。
TD853.34
A
1001-1250(2014)-04-022-06
