一类p-Laplacian椭圆抛物型偏微分方程解的唯一性

袁海君

( 山东商业职业技术学院,山东 济南 250103 )

一类p-Laplacian椭圆抛物型偏微分方程解的唯一性

袁海君

( 山东商业职业技术学院,山东 济南 250103 )

主要利用了凸集的有序性，证明了一类p-Laplacian椭圆抛物型偏微分方程即：ρt(u)-▽·(|▽u|p-2▽u)=f(t,x)的解的唯一性，其定义在区域(0,T)×Ω，其中Ω是RN的一个有界区域(N≥1)，边界∂Ω是C2光滑的p≥2，ρ(u(0,x))=ρ0。

p-Laplacian；凸集； 有序性； 唯一性

1 引言

目前，物理学、生物化学、医学、控制论等学科的实际问题均可以通过偏微分方程来解决。人们对其的研究日渐深入，并取得了很多重要的成果，使得这方面的理论日趋完善。

本文研究一类具有初边值问题的椭圆抛物型偏微分方

ρt(u)-▽·(|▽u|p-2▽u)=f(t,x)

(*)

其中，(t,x)∈(0,T)×Ω且ρ(u(0,x))=ρ0

其中Ω是RN的一个有界区域(N≥1)，ρ:R→R是有界的非减的Lipschitz连续的函数，其中Lipschitz常数Cp>0。

近年来具有上述初值的椭圆抛物型方程解的问题受到越来越多的关注，在工程力学方面应用性越来越广泛。文献[1]已经证明了该方程解的存在性。接下来利用解的有序性来证明该方程解的唯一性。

2 几个引理

首先结合文献[2]做如下假设

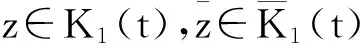
为了去陈述下面的定理，接下来定义在凸集间的有序关系。

下面的引理主要是和解的有序性有关，而解的有序性又是由给定的数ρ0，f和K1(t)来决定的。

证明： 首先，观察下面的两个等式

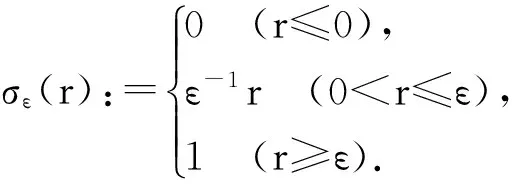
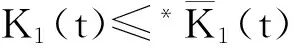
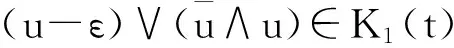
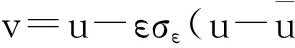
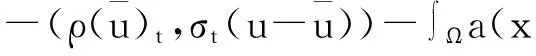
将(2.1)和(2.2)相加，得下面(2.3)成立：

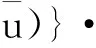
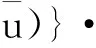
进行讨论：由a(x,▽(u))=|▽u|p-2▽u，有

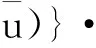
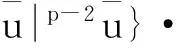
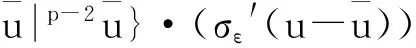
由a(s)=|s|p-2s有a′(s)=(p-1)|s|p-2≥0。因而a(s)是单调递增的，即下面(2.4)和(2.5)成立：

(a(s1)-a(s2))·(s1-s2)≥0.

因此，通过(2.3)结合文献[3]有

因此将(2.3)式和(2.4)式结合，对几乎处处的t∈[0,T]和任意的ε>0

3 结论

定理(解的唯一性)某一确定的f∈W1,2(0,T;H)和ρ，且对某个u0∈K1(t)有ρ0=ρ(u0)，那么问题(P;ρ0,f,K1(t))的解是唯一的。

[1]袁海君, 一类p-Laplacian椭圆抛物型偏微分方程解的存在性[J],湖南工程职业技术学院学报2013,(4)18-21.

[2]M. Kubo and N.Yamazaki. Elliptic-Parabolic Variational Inequalities With Time dependent Constants[J].Discrete and continous dynamical systems.Vol.19, Number.2. 2007, pp.335-359

[3]N. Kenmochi and I. Pawlow.Parabolic-elliptic free boundary problems with time-dependent obstacles[J].Japan J.Appl.Math.,5(1988),87-121

(责任编辑：孙强)

The Uniqueness of Solution to a cClass of P - Laplacian Elliptic- Parabolic Equation

YUAN Hai-jun

( Shandong Institute of Commerce and Technology, Jinan, Shandong 250103, China )

Using the order of the convex, this thesis investigates the uniqueness of solution to a class of p-Laplacian elliptic-parabolic equation ρt(u)-▽·(|▽u|p-2▽u)=f(t,x) in(0,T)×Ω,whereΩ⊂RNwih ∂Ω of C2class,p≥2,ρ(u(0,x))=ρ0.

p-Laplacian；convex；order； uniqueness

2014-08-10

袁海君(1986-)，女，湖南邵阳人，人文学院助教，研究方向为偏微分方程的应用与数学建模。

O172

A

1671-4385(2014)05-0124-03