对称受拉杆系的荷载—位移关系分析
2014-08-08杨小令
陈 诚 王 洁 杨小令
(扬州大学水利与能源动力工程学院,江苏 扬州 225127)
对称受拉杆系的荷载—位移关系分析
陈 诚 王 洁 杨小令*
(扬州大学水利与能源动力工程学院,江苏 扬州 225127)
对称受拉杆系的轴力及结点位移计算方法都存在一定的局限性,而通过建立荷载—结点位移函数关系式,可解决瞬变体系结点位移计算问题,同时提出了超静定结构的各杆轴力比值公式,为结构优化设计提供了理论依据。
瞬变体系,弹性形变,非线性关系,结构优化
0 引言
在对称受拉杆系结点位移及轴力的计算中,往往在小变形假设[1]前提下采用原尺寸原理和“以直代曲”的静力学解法,计算时造成了一定的误差。目前亦有采用迭代法[2]和能量法[3]进行求解的探索,迭代法仅仅在内力的相对误差计算中取得一定突破,而能量法在计算过程中仍借助“以直代曲”的方法进行求解,两者均有一定的局限性。本文以建立荷载和结点位移的函数关系式为出发点,做出荷载—结点位移曲线,并将其同时应用于大、小变形时杆系的轴力、位移分析中。对于静定结构,证明了利用静力法与能量法进行求解的等价性,解决了瞬变体系的结点位移计算问题[4],并且证明了在小变形假设前提下荷载—结点位移函数与现有材料力学结果的一致性。在超静定结构中,推导出杆件轴力比值的精确表达式,在小变形假设前提下借助对勾函数的性质分析荷载和结点位移的变化关系,并进行结构的初步优化设计,创造了一定的工程应用价值。
1 对称受拉杆系的静定结构计算
考虑由两根线弹性杆件连接而成的平面对称桁架结构,如图1所示,在铰A处作用一集中力P,由0开始缓慢增加,方向竖直向下,大小为P,B,C均为固定铰支座。
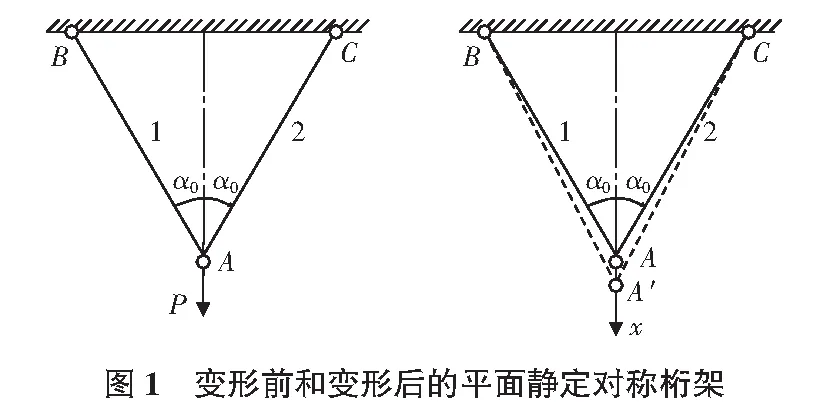
若已知加载前1,2两杆的轴力为FN=0,长度均为l0,与竖直线的夹角均为α0(α0∈[0,90°]),经拉伸变形后1,2两杆的轴力为FN。长度均变为l(根据对称性易知两杆伸长量相等),与竖直线的夹角变为α。两杆的弹性模量均为E,横截面积均为A。经拉伸后结点A的竖直位移为x。
1)几何关系:
铰A的竖直位移:
x=lcosα-l0cosα0
(1)
由式(1)得:
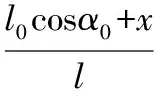
(2)
利用余弦定理[5],得:
(3)
由式(3)得:
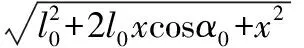
(4)
1,2杆的伸长量:
Δl=l-l0
(5)
2)物理关系:
胡克定律(任意时刻1,2杆的伸长量):
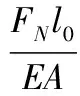
(6)
3)任意位置平衡关系:
P=2FNcosα
(7)
根据以上已知各式,求得轴力与结点位移的关系:
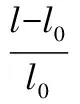
(8)
荷载与位移的关系:

(9)
将式(4)代入得:
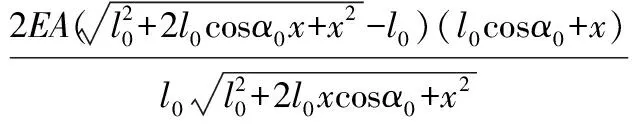
(10)
式(10)表明在EA,l0和cosα0一定的情况下,荷载P是位移x的单值函数,此关系为非线性关系。
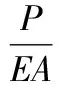
(11)
令δ=x/l0,代入得:
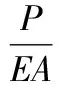
(12)
分别取α0=0°,30°,45°,60°,75°,90°,δ在0到1之间取值(如果将1,2杆换成橡皮筋或弹簧,则在弹性变形范围内,δ完全有可能达到1),利用Matlab软件画出荷载—位移函数(如图2所示)。
从函数图像(曲线由上而下分别对应α0=0°,30°,45°,60°,75°,90°)可以看出:
1)α0=0°时,荷载—位移呈线性关系,曲线斜率为2。当初始角大于0°,荷载—位移呈凹函数关系,且初始角越大,曲线的凹性越明显。这表明随着荷载的均匀增加,位移的增加速率越来越缓,且初始角越大的杆系,这种性质越明显。
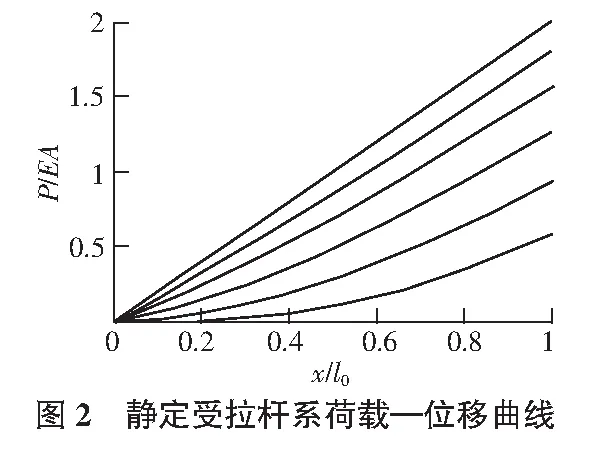
2)在施加同等荷载且杆长相同的情况下,初始角越大,铰A的位移越大。即杆长一定,初始角越小结构越安全。
3)对于弹性模量很小的受拉系统(比如弹簧、橡皮筋),将δ的范围继续增大,则各条曲线有呈近似线性关系的趋向。
特别地,当α0=0°时,将cosα0=1代入并化简得:P/EA=2δ,为线性关系。
而当α0=90°时,为瞬变体系,将cosα0=0代入得:
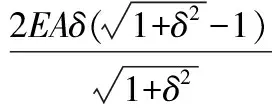
(13)
此时荷载—位移函数关系依然成立,这说明基于荷载—结点位移函数关系式解决受拉杆系结点位移问题具有更强的实用性。
当x≪l0时,将x视作l0的高阶无穷小量,通过分子有理化可得:
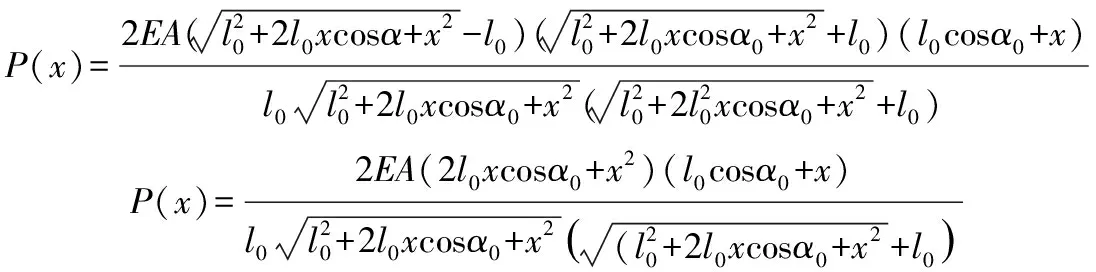
(14)
略去无穷小量得:
这与利用材料力学推得的熟知的结果是一致的,同时也验证了小变形假设在处理受拉杆系位移问题中的可行性。
2 对称受拉杆系的超静定结构计算
下面考虑3根杆同时受拉的超静定结构[6,7],其中1,2两杆轴力FN1=FN2,原长l0,与竖直线的夹角均为α0(α0∈[0,90°)),经拉伸变形后长度均为l,与竖直线的夹角为α。3杆轴力为FN3,方向竖直,原长l0cosα0。3根杆的弹性模量均为E,横截面积A(当α0=90°时,3杆长度为0,可视为静定结构中α0=90°的情况进行考虑)。
变形前和变形后的平面超静定对称桁架见图3。
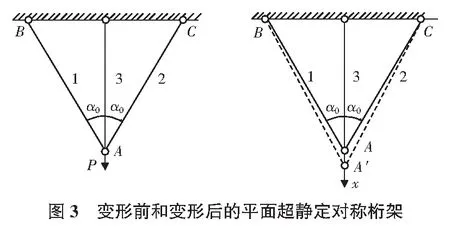
1)几何关系:
铰A的竖直位移:
x=lcosα-l0cosα0
(15)
1,2杆的伸长量:Δl=l-l0,3杆的伸长量:Δl′=x
(16)
余弦定理:
(17)
2)物理关系:
胡克定律(任意时刻杆的伸长量):
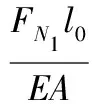
(18)
3)任意位置平衡关系:
P=2FN1cosα+FN3
(19)
轴力与位移的关系:
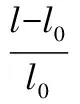
(20)
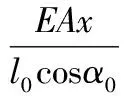
(21)

(22)
当x≪l0,将δ视为无穷小量,且初始角一定,cosα0视为常数,则有:

(23)
利用罗必达法则,上下同时对δ求导得:

(24)
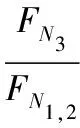
分析式(24)可知,在小变形情况下,3杆与1,2两杆的轴力之比等于1/cos2α0。所以初始角不宜过于接近90°,以免3杆的轴力过大发生受拉破坏导致结构失稳[8,9]。可以考虑增大3杆的EA以优化杆系结构设计。
利用上述各式,求得荷载与位移的关系:
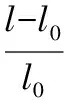
(25)
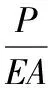
(26)
分子有理化得:
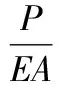
(27)
当x≪l0时,将x视作l0的高阶无穷小量,略去δ的高阶无穷小并化简得:
(28)
上式同样表明在EA,l0和cosα0一定的情况下,荷载P是位移x的单值函数。
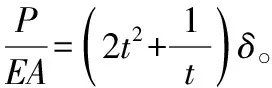

分别取α0等于0°,15°,30°,45°,60°,75°,85°,δ在0~1之间取值,并且用Matlab软件来绘制荷载—位移曲线图,如图4,图5所示。
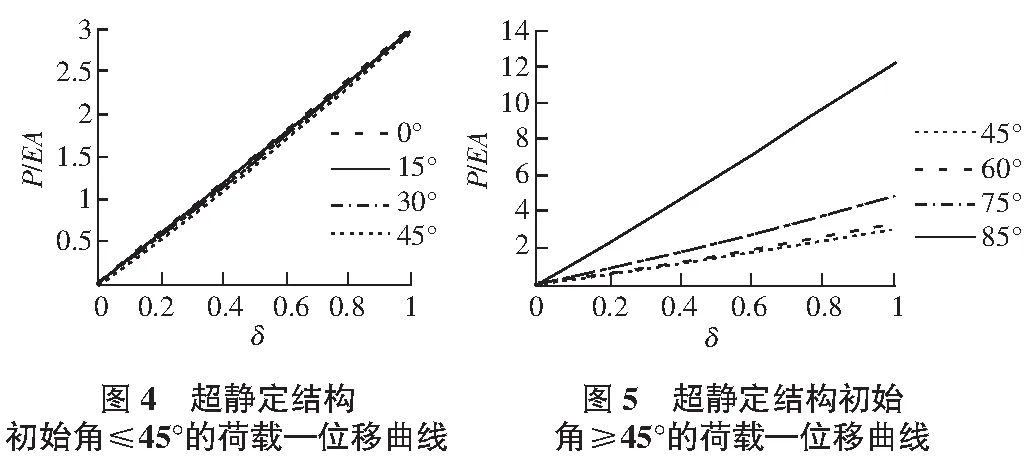
通过上述曲线可以得出以下结论:
1)在超静定结构中,不论初始角为多少,荷载与位移为近似线性关系;
2)当α0≤51°时,荷载—位移变化关系变化不大,曲线斜率非常接近;当α0>51°时,随着初始角的增大,在位移、杆长一定的情况下,荷载呈加速上升趋势。说明对于超静定结构,只要3杆处于弹性变形范围内,初始角越大,杆系越稳定;
3)相比于静定结构,在位移相同的情况下,超静定结构的荷载要大于静定结构,且初始角越大,稳定性的提高越明显。
3 结语
在建立杆系结构弹性位移与荷载的函数关系问题处理中,以上方法得到了相对精确的结果,并且具有普适性,而在忽略微小变形的情况下结果与小变形求得的结果相一致,这本身也印证了这种方法的科学性,可以说它是对材料力学中对称受拉杆系的深入探讨。在静定结构与超静定结构的比较中,我们发现对于初始角小于51°的受拉杆系,在静定结构的基础上增加杆件转化为超静定结构,对于稳定性的提高并不明显,安全度提高为原来的2倍以内。当初始角大于51°,超静定结构的稳定性远远好于静定结构。为了保证3杆在较大荷载作用下处于弹性变形范围之内,可以增大3杆的横截面积和弹性模量,以提高其弹性极限和抗拉强度,这对实际工程应用也具有一定的应用价值。
[1] 郑家树.结构力学中的假设及其对教学的作用[J].西南民族大学学报(自然科学版),2005,31(5):838.
[2] 邓宗白,陶秋帆,金 晖.关于材料力学中小变形问题的讨论[J].力学与实践,2009,31(4):72-76.
[3] 丁小艳,李冠磊.基于能量法求解力学问题[J].宁波职业技术学院学报,2006,10(15):20-23.
[4] 张效松.简单平面桁架结点位移确定的一种方法[J].力学与实践,1998,20(1):54-55.
[5] 孙铁斌.余弦定理在力学解题中的应用[J].中学物理教学参考,2001,30(2):28-30.
[6] 常学平,王 维,蒋 平,等.拉、压静不定问题变形几何分析中存在的问题[J].力学与实践,2008,30(2):89-90.
[7] 熊慧而,罗松南.杆系静定结构的变形协调条件[J].力学与实践,1996,18(6):48-49.
[8] [美]A.查杰斯.结构稳定理论原理[M].唐家祥,译.西安:人民出版社,1982:71-82.
[9] 陈绍藩,吴 博.拉—压杆件的稳定承载能力[J].建筑钢结构进展,2007,9(1):41-45.
[10] 马洪波.基于概率的杆系结构可靠性分析及优化设计[D].西安:西安电子科技大学,2001:31-37.
[11] 李 波,李建营,周 鑫.空间杆系结构布局优化的能量法[J].机械设计与研究,2010,26(2):28-31.
Studyontheload-displacementrelationshipofthesymmetricalrod-systemsundertensionloading
CHENChengWANGJieYANGXiao-ling*
(CollegeofHydraulic,EnergyandPowerEngineering,YangzhouUniversity,Yangzhou225127,China)
Limitations still exist in the present computational methods of the axial force and the node displacement in the axial-symmetric bar systems. The computational problem of the node displacement in the instantaneously changeable system can be actually solved by founding a load-node displacement function relationship. At the same time, a ratio formula presented for the axial force of each rod piece in statically indeterminate structure can provide theoretical basis for optimum structural design.
instantaneously changeable system, elastic deformation, non-linear relationship, structure optimization
1009-6825(2014)14-0057-03
2014-03-02
陈 诚(1993- ),男,在读本科生; 王 洁(1993- ),女,在读本科生; 杨小令(1960- ),男,讲师
TU311.4
:A
