基于断裂点理论与加权Voronoi图的京津冀地区城市影响范围研究

2014-08-08谷景祎周廷刚郭丽敏

地理与地理信息科学 2014年1期

谷景祎，周廷刚，郭丽敏

（三峡库区生态环境教育部重点实验室，西南大学地理科学学院，重庆 400715；重庆市地理空间信息工程技术研究中心，重庆 401147）

0 引言

城市影响范围是中心城市在经济投资、市场分配、产业扩散、货物流通、人才流动等诸多社会经济因素的共同作用下对周围地区影响所能达到的最大地域范围，是一个充满相互作用的复杂区域社会经济系统［1］。城市影响范围的界定是研究城市与周围城市、区域之间相互作用中的一个重要内容，已成为近些年研究的热点［2，3］。在目前已有的几种界定城市影响范围的方法中，利用断裂点模型和Rd链等方法可以生成任意两个相邻城市间的影响范围分界［1］，但针对多个城市间影响范围的界定较为复杂，主要利用场强分析法、基于Voronoi图的空间分析法及其改进模型等方法［4－9］。本文选取了评价城市综合实力的20个指标，运用统计分析和数据变换的方法，确定京津冀地区14个地市的中心性强度。结合城市断裂点理论和加权Voronoi图方法，采用基于欧氏距离的栅格算法界定并生成了京津冀地区各地市的影响范围，实现了中心城市的确定和城市经济影响区的划分，旨在为京津冀地区的城市规划和区域经济决策提供参考，更好地实现京津冀地区经济一体化发展。

1 断裂点理论

1949年康弗斯（P.D.Converse）在赖利（W.J.Reily）“零售引力规律”的基础上提出断裂点理论［10］，其计算模型为：

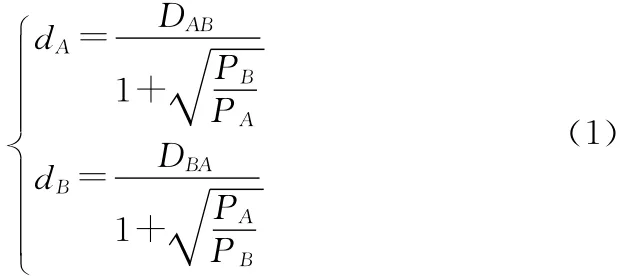
其中，dA和dB分别为A、B两座相邻城市到断裂点的距离，DAB和DBA为两城市间距离，PA和PB分别为这两座城市的人口。

然而从现实角度看，断裂点理论存在很多不合理的地方［7］：首先，城市人口数量不能完全体现出城市的综合实力；其次，断裂点理论公式只提供两座相邻城市间的断裂点的计算，难以计算由多个城市构成的复杂城市体系中的多个断裂点。

本文为能较好地反映城市综合实力，通过一套评价指标体系计算获得城市的中心性强度值，并以此代替城市人口。采用欧氏距离，则有DAB＝DBA。将式（1）进行变换得：

由式（2）可以看出，两座相邻城市到其断裂点的距离与两城市的中心性强度的平方根呈正比。

设a1和a2是属于同一均质平面域的2个相邻生长核的扩张速度，t是它们同时扩张到断裂点所需的时间，则有d1＝a1t，d2＝a2t，将其带入式（2）中可得：

由此可见，生长核的扩张速度是每座城市中心性强度值的平方根，而不是各城市的中心性强度值。

2 Voronoi图模型

2.1 常规Voronoi图

狄利克雷（Dirichlet）于1850年首先讨论了Voronoi图的概念，其定义如下［11］：假设P为位于同一平面上的点集，P＝｛p1，p2，…，pn｝其中任意2点不共线，任意4点不共圆，则任意一点pi的Voronoi图定义为：

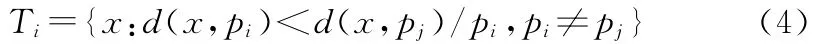
其中，d为欧氏距离。

Voronoi图某一网格中的任意一点到其他网格生长核的距离都大于到该网格生长核的距离。但在界定城市的空间影响范围时，常规Voronoi图并未将城市综合实力这一重要因素纳入考虑范围，仅将与中心城市间的距离作为唯一的影响因素，因此无法较好地模拟实际情况。

2.2 加权Voronoi图

加权Voronoi图是众多Voronoi图中较为常用的一种［7，11］。其定义为：

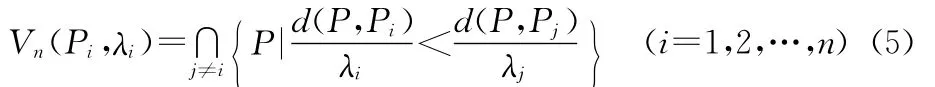
式中：Pi（i＝1，2，…，n）为二维欧氏空间上的n个点；λi（i＝1，2，…，n）为给定的n个正实数。将平面分成n部分，由Vn（Pi，λi）确定的对平面的分割称为点上加权的Voronoi图，称λi为Pi的权重［12］。当各点的权重相等时，式（4）与式（5）等价。

加权Voronoi图网格中的任意一点到其所属网格生长核的距离与该点到其他网格生长核的距离之比小于两生长核的权重之比。由此可见，在各生长核权重存在明显差异的情况下，利用加权Voronoi图进行空间剖分更为合适。

3 基于断裂点理论与加权Voronoi图的城市影响范围划分

京津冀地区地处环渤海经济区的核心区域，包含北京和天津2个直辖市以及河北省的11个地级市。本文以各地市的主城区为对象，研究其对周边区域的影响力。考虑到作为天津市组团城市的滨海新区的迅速崛起，其综合实力超过了河北诸多地市，本文将其作为独立的对象纳入研究范围。

3.1 城市综合实力评定

为了能够比较全面地反映城市对其周边区域的多方面影响，应结合社会学、区域经济学和城市地理学基本原理，根据可持续发展原则、系统性原则、全面性原则、明确性原则、可行性原则等建立城市综合实力评价指标体系，多角度、多层面描述城市综合实力。笔者结合京津冀自身特点，并借鉴前人的研究成果［13，14］，选取2011年京津冀三地4个子系统，共20个指标，即城市社会经济发展水平指标（10个），包括城区常住人口、国内生产总值、财政收入、利用外资总额、消费品零售总额、城镇固定资产投资、民用汽车拥有量、高等学校专任教师数、公共图书馆藏书量、医生人数；城市建设水平指标（4个），包括城区建成区面积、人均住房面积、道路面积、绿地面积；区域发展水平指标（4个），包括地区城镇化水平、人均国内生产总值、城镇人均可支配收入、农民人均纯收入；城市基础条件指标（2个），包括交通可达性以及矿产、旅游资源条件。运用主成分分析方法，计算各城市综合实力得分（表1）。

表1 14个地市的综合实力排名Table 1 The comprehensive strength rank of fourteen cities

城市影响范围主要受制于中心城市的中心性强弱［15］，本文以城市综合实力表征中心性强度，明显可见有些城市的综合得分为负值，利用公式（3）计算断裂点位置时会涉及开方运算，显然直接代入负值是不可行的。为保证计算数据不出现负值，需要对各地市的综合实力得分进行数据变换，且不能改变原有数据的次序特征，因此选择在闭区间［1，10］内对各地市的综合得分进行最小－最大规范化，得到中心性强度值（表1）。

3.2 城市影响范围与经济影响区划分

目前，利用Voronoi图确定中心城市并划分经济影响区的方法，除了王新生等提出的基于常规Voronoi图分析城市体系的方法［16］，还有闫卫阳等提出的基于加权Voronoi图确定中心城市并划分城市经济区的方法［9］。该方法构建以中心性强度值为权重的加权Voronoi图，通过网格的包含关系筛选中心城市，这与城市相互作用理论和断裂点理论并不完全吻合。实验证明，将该方法用于京津冀地区，只能确定北京这一个中心城市，无法进一步详细划分，与实际情况并不完全相符。为此，本文对此方法进行了一定的改进，具体方法步骤如下。

首先，采用基于断裂点理论的加权Voronoi图方法，界定并生成研究区域内各地市的城市影响范围。以京津冀地区14个地市的城市中心性强度值的平方根为速度，以城区作为生长核向周围扩展，最终形成由多个闭合边界组成的京津冀地区城市影响范围加权Voronoi图（图1）。图中闭合单元的边界就是相邻城市间城市影响力的断裂弧，其包围的内部区域就是该城市的影响范围。

图1 城市影响范围Fig.1 The influencing regions of central cities

其次，通过分析基于断裂点理论的加权Voronoi图中的网格间相互关系，在确定区域中心城市的基础上初步形成城市经济影响区的划分方案，分析过程如下：1）逐一分析图1中相邻网格间的包含关系。影响范围被包含在其他城市影响范围内的城市不具备成为区域中心城市的条件。这样，张家口和承德就被排除，候选中心城市减为12个。2）分析图1中每个网格的邻近关系。空间分布邻近的两个影响范围，断裂弧的弯曲方向总是指向中心性强度更大的城市，即指向更具吸引力的城市。在考虑影响范围面积分布均衡的前提下，归并在空间分布上邻近的影响范围，使其成为一个组团。这样可将京津冀地区划分为5个城市组团：北京组团（包含北京、张家口、承德、廊坊、保定），唐山组团（包含唐山、秦皇岛），天津组团（包含天津、滨海新区、沧州），石家庄组团（包含石家庄、衡水），邯郸组团（包含邯郸、邢台）。以上述组团为单位，利用该方法对面积较小的城市组团进一步划分，可将唐山组团并入天津组团，邯郸组团并入石家庄组团，从而得到3个较大的一级城市组团，形成城市经济影响区的初步划分方案。3）逐一确定各个城市组团的中心城市。将每个组团内中心性强度值最大的城市确定为该组团的中心城市，这样确定一级中心城市为北京、天津、石家庄，二级中心城市为唐山、邯郸。

最后，依照经济影响区划分原则，对初步形成的基于加权Voronoi图的城市经济影响区划分方案进行调整。需要在保持区县行政区划完整性、影响区内自然条件基本一致的同时，充分考虑区县之间的交通通达度、产业结构的互补性及可持续发展潜力等多种因素，对京津冀地区的城市经济影响区初步划分方案进行调整（图2），将研究区域划分为3个城市群、13个城市经济影响区，划分结果见表2。

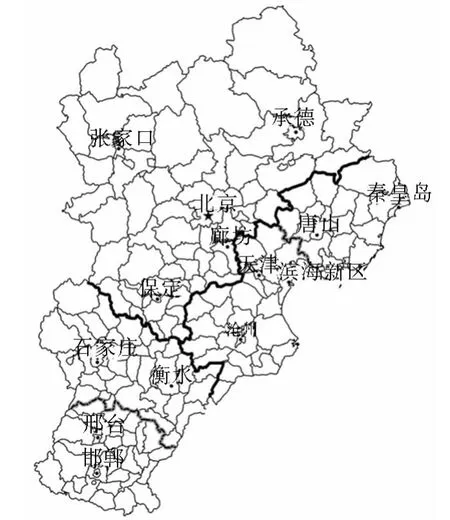
图2 城市经济影响区划分方案Fig.2 The zoning plan of urban economic regions

研究京津冀地区的城市影响范围，并对城市经济影响区进行划分，有利于辨识三地在区域发展中的关系。北京作为区域重要中心城市，需要明晰其能服务的最大区域范围，突破省界承担起带动京津冀地区整体发展的任务。天津是区域内最大的沿海开放城市，应当明确其与腹地间的相互关系，充分利用经济腹地的优势促进自身发展，同时有效带动腹地经济快速增长。经济相对落后的河北应当有效利用京津两地的功能分散完成相关产业对接，吸纳高新技术及人才，充分利用环绕京津的区位优势，加快河北社会经济发展速度。

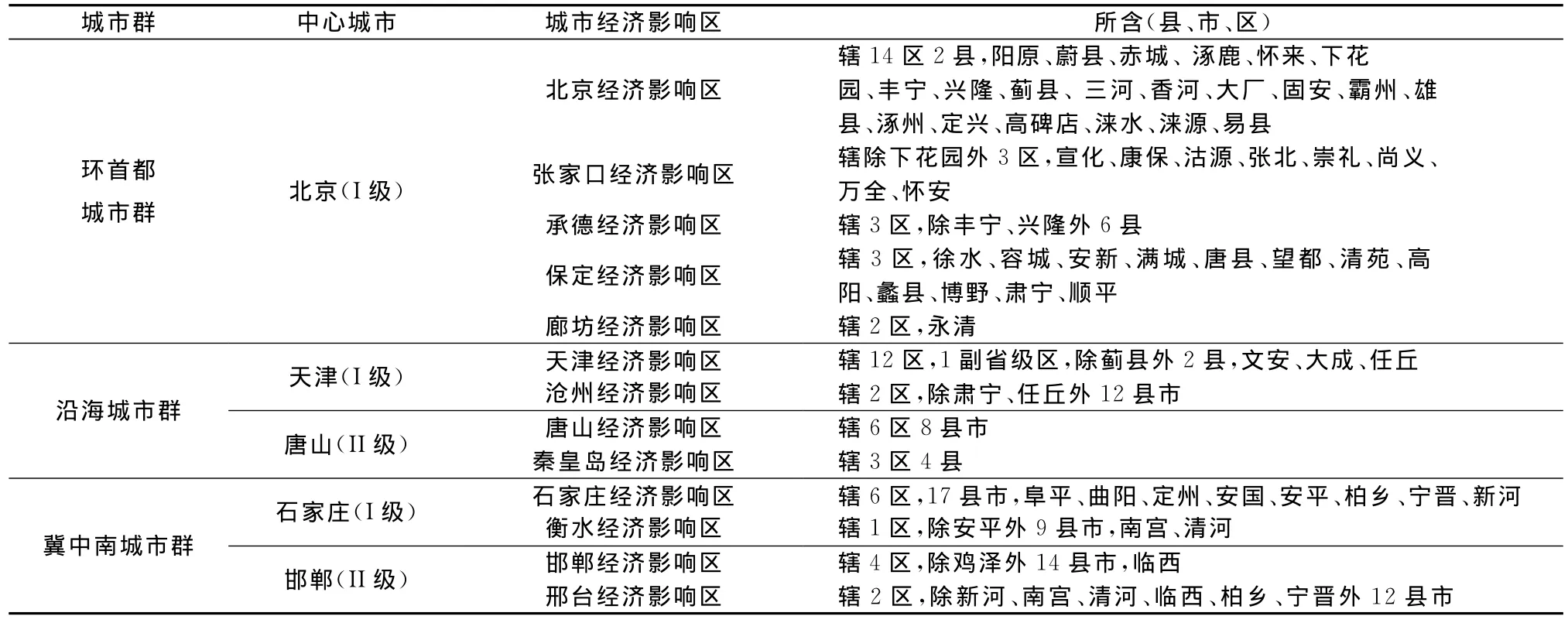
表2 城市经济影响区划分方案Table 2 The plan of urban economic region dividing

4 结论与讨论

用上述方法确定的城市影响范围是由综合实力和区位条件共同决定的，其大小并不完全是城市综合实力的体现。例如城市综合实力最弱的衡水市，由于和周边城市的综合实力差距较小且距离较远，所以拥有较大的城市影响范围；城市综合实力排第7位的廊坊市由于夹在京津之间而拥有最小的影响范围。与其他利用Voronoi图确定中心城市并划分经济影响区的方法相比，利用基于断裂点理论的加权Voronoi图确定区域中心城市，符合基于断裂点理论进行的推论，即在界定和生成城市影响范围时，以城市中心性强度值的平方根为速度向周围扩张能更好地模拟现实情况。实验证明，在对拥有特大城市的局部区域进行城市经济影响区划分时，这种方法更为合适。

基于断裂点理论的加权Voronoi图方法仍然处于发展阶段，有待完善。在界定城市空间影响范围时，它没有充分考虑现实社会中的自然、文化等因素的影响。此外，由众多行政区划以及各种自然、社会、经济要素形成的空间体系是一个复杂的系统，不应忽略周边地区对研究区域的影响。本文研究的是京津冀地区的城市影响范围，在交通与通信越发方便的今天，需要考虑环渤海经济圈对所研究区域的影响，甚至是更大范围地区的影响。以上问题有待在研究中解决，从而使理论得到完善。

［1］顾朝林.中国城市地理［M］.北京：商务印书馆，2004.

［2］许学强，周一星，宁越敏.城市地理学［M］.北京：高等教育出版社，2009.

［3］谢顺平，冯学制，王结臣，等.基于网络加权Voronoi图分析的南京商业中心辐射域研究［J］.地理学报，2009，64（12）：1467－1476.

［4］王新生，刘纪远，庄大方，等.Voronoi图用于确定城市经济影响区域的空间组织［J］.华中师范大学学报（自然科学版），2003，37（2）：256－260.

［5］ OKABE A，SUZOKI A.Location optimization problems solved through Voronoi diagrams［J］.European Journal of Operational Research，1997（98）：445－456.

［6］ OKABE A.Spatial Tessellation：Concept Sand Applications of Voronoi Diagrams（2nd edition）［M］.Chichester：John Wiley，2000.1－671.

［7］王新生，李全，郭庆胜，等.Voronoi图的扩展、生成及其应用于界定城市空间影响范围［J］.华中师范大学学报（自然科学版），2002，36（1）：107－111.

［8］李圣权，胡鹏，闫卫阳.基于加权Voronoi图的城市影响范围划分［J］.武汉大学学报（工学版），2004，37（1）：94－97.

［9］闫卫阳，郭庆胜，李圣权.基于加权Voronoi图的城市经济区划分方法探讨［J］.华中师范大学学报（自然科学版），2003，37（4）：567－571.

［10］张哲，薛惠锋.基于加权Voronoi图的宝鸡地区城市影响区的划分［J］.计算机仿真，2008，25（6）：261－264.

［11］范熙伟.加权Voronoi图矢量生成算法研究及其实现［D］.西安：西北大学，2011.

［12］张有会.线段加权的 Voronoi图［J］.计算机学报，1995，18（11）：822－829.