特高压交流输电线路铁塔质量计算

杨博，李陶波，杨茂亭，王爱华，马芳

(1. 山东电力工程咨询院有限公司，济南市 250013；2. 山东理工大学，山东省淄博市 255049)

特高压交流输电线路铁塔质量计算

杨博1，李陶波1，杨茂亭2，王爱华1，马芳1

(1. 山东电力工程咨询院有限公司，济南市 250013；2. 山东理工大学，山东省淄博市 255049)

在新建工程的可研和初步设计阶段，从新的设计条件出发推算铁塔质量，可以帮助完成杆塔选型和规划、路径比选、杆塔优化排位等，对提高概算准确性、节省工程造价具有重要意义。为此在特高压直流输电线路铁塔质量分析计算的基础上，对荷载更大、塔头布置形式多样化的特高压交流输电线路铁塔质量进行深入研究，并推广至500 kV超高压交流输电线路领域。采用“1 000 kV浙福线工程”及“500 kV铁塔通用设计”中不同塔型、呼高所对应的质量数据样本，建立回归分析数学模型，使用Matlab软件得到质量计算关系式。将计算结果与实际铁塔质量作比较，进一步验证了该方法及公式的准确性和适用性。对于重覆冰区线路，则应考虑导地线脱冰跳跃时产生不平衡张力的影响，修正和补充质量计算关系式。

特高压交流；超高压；回归分析；铁塔质量(塔重)；荷载；重覆冰区

0 引 言

铁塔质量(或称塔重)指标是输电线路优化设计首要考虑的因素，需要随时调用，但准确地计算不同新塔型及呼高铁塔质量的工作量很大，且也多在施工图设计阶段才能完成，无法用于工程设计的前期阶段；若采用常规力矩关系式[1]计算质量，变量过多，操作繁琐，误差也大。文献[2]使用回归分析方法，对特高压直流铁塔通用设计的质量数据样本进行分析和计算，得到了质量计算关系式，由该式得到的质量计算结果与通用设计质量作比较，准确度高，简便实用[2]。

与特高压直流±800 kV线路相比，特高压交流1 000 kV线路铁塔荷载更大、塔头布置形式更加多样化，其特点在于：(1)直流线路导线为两极，每极导线六分裂，交流线路单回路为三相导线、双回路为六相导线，每相导线八分裂。(2)直流线路采用导线水平排列T字型铁塔；交流线路的单回路直线塔采用导线水平排列酒杯型塔、三角排列猫头型塔，耐张塔采用三角排列干字型塔；交流双回路直线或耐张塔均采用导线垂直排列伞形塔。

另一方面，线路经过重覆冰区，在导地线脱冰跳跃时产生不平衡张力的影响下，铁塔质量计算关系式也需要作相应修正和补充，否则误差较大。

综上，本文在特高压直流线路铁塔质量分析和计算的基础上，深入研究特高压交流线路铁塔质量的计算方法，并推广至500 kV超高压交流线路领域检验该方法。以“浙北—福州1 000 kV交流线路工程(下称浙福线)”及“500 kV铁塔通用设计”[3]为依托，采用回归分析方法[4-6]，借助Matlab软件[7-10]分析铁塔质量与呼高、荷载[11-14]等变量之间的规律性；根据不同导地线、气象区(包括重覆冰区)、地形、海拔高度、单双回路、塔头布置的各种塔型质量数据样本，整理归纳出质量计算关系式，并将计算结果与实际铁塔质量进行比较，进一步验证该方法的正确性和适用性，并作相应的补充。

1 回归分析原理

(1)最小二乘法计算参数估计值。令y=f(x,θ)，求参数估计值θ，使得实际值与真值的误差平方和Q达到最小值，即：

(1)

(2)显著性检验。R2可决系数为

(2)

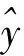
2 1 000 kV输电线路铁塔质量计算分析

2.1 数据样本的选取

由于目前1 000 kV线路铁塔尚没有制定通用设计，因此以浙福线塔型为样本进行算例分析。分别选用系列1单回路和系列13双回路塔型，系列13双回路塔型为浙福线套用1 000 kV“皖电东送”工程的塔型，更具有适用性。

系列1单回路设计条件：导线型号为8×JL/G1A—500/45，地线型号为2×JLB20A—170，设计最大风速为27 m/s，覆冰厚度为15 mm，海拔高度为500 m以下。该系列直线塔采用导线IVI串水平排列酒杯塔，耐张塔采用三角排列干字型塔，直线塔采用7塔方案，耐张塔采用20°分档的4塔方案，Ⅳ型塔档位取60°～90°。

系列13双回路设计条件：导线型号为8×JL/G1A—630/45，地线型号为2×JLB20A—185，设计最大风速为27 m/s，覆冰厚度为10 mm，海拔高度为500 m以下。该系列直线塔采用导线I串垂直排列伞形塔，直线塔采用7塔方案，耐张塔采用10°分档的7塔方案，Ⅶ型塔档位取60°～90°。

2.2 铁塔质量与呼高的关系

铁塔呼高越高，质量越大。指数模型拟合非线性离散样本时精度高，收敛性、稳定性更好，因此运用Matlab对可确定铁塔质量W与呼高h的回归指数模型曲线如式(3)所示。

W=aebh

(3)

图1所示为单、双回路主力塔型Ⅳ型直线塔铁塔质量对呼高的指数关系，单回路直线塔呼高指边(中)相呼高，双回路直线塔呼高指上相呼高，2层间距和取40 m。使用式(3)拟合质量时平均误差不大于2.4%。由表1可知，95%置信区间下进行参数估计，可决系数R2非常接近1，关系式合理。

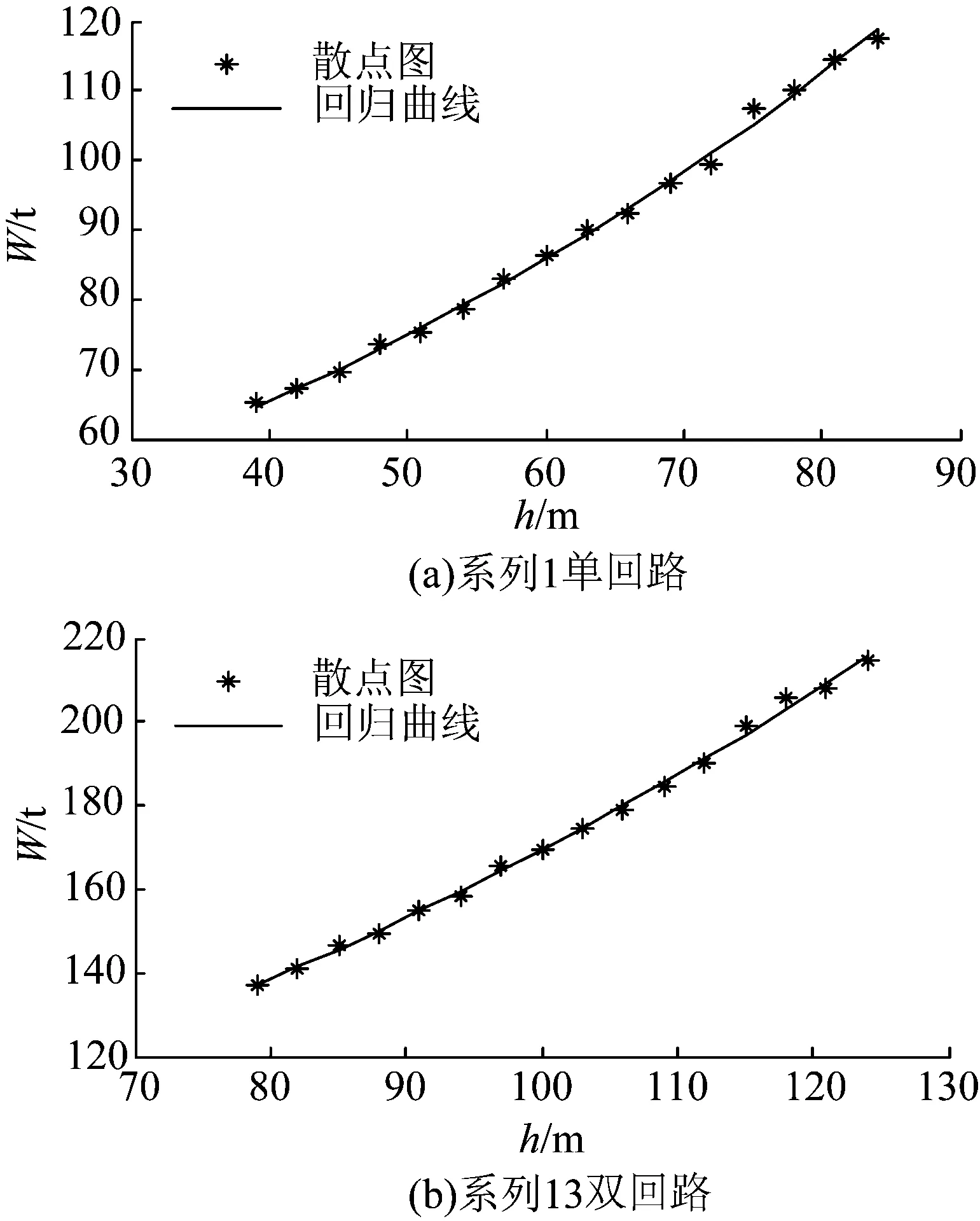
图1 单、双回路直线塔质量与呼高回归曲线

单回路和双回路b值的范围分别为0.012 3～0.014 2和0.010 1～0.012 5，铁塔级间(3 m为1级)单回路比值为e0.012 3×3=1.038～e0.014 2×3=1.043，双回路比值为e0.010 1×3=1.031～e0.012 5×3=1.038。可见b值基本相同，a值则随塔型的不同而变化。若只用指数关系来拟合，虽然可满足精度要求，但需对每种型塔都作分析计算，而不适用于该系列各种塔型，其通用性差，计算工作量大。塔型质量差异的另一个主要因素是荷载差异，因此下面需要引入荷载进行质量计算。

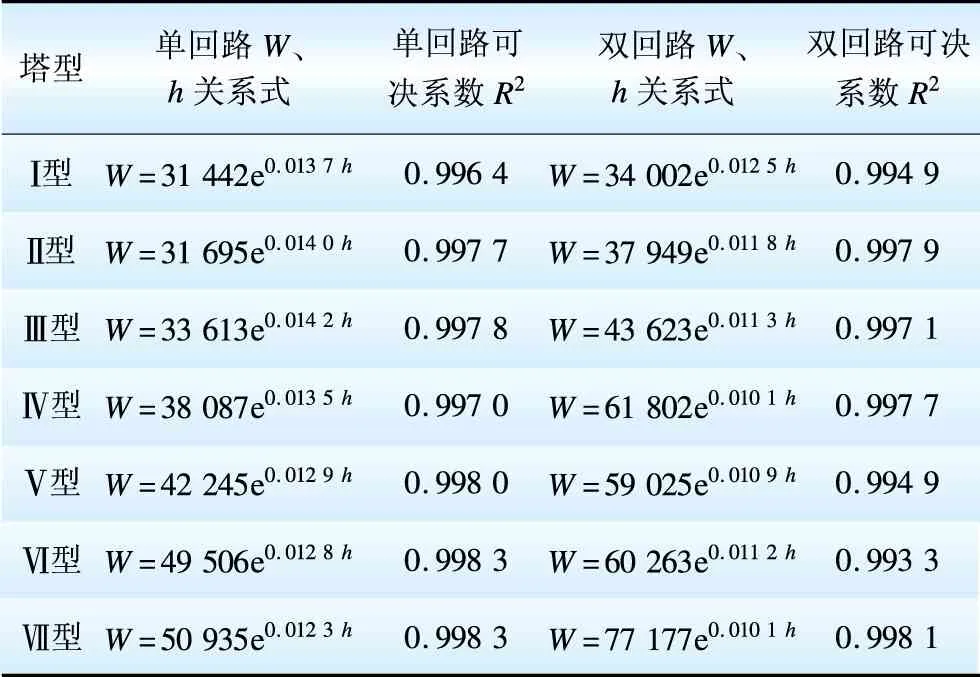
表1 直线塔质量与呼高关系式

2.3 铁塔质量与荷载的关系

铁塔设计荷载越大，质量越大。当单回路边(中)相呼高取值为66 m，双回路2层间距和取40 m，上相呼高为106 m，对质量W、导地线最大风工况下水平荷载fh、覆冰工况下垂直荷载fv进行回归分析，得到铁塔质量与荷载回归线性曲线，如图2所示，关系式如下：

W=β0+β1fh+β2fv

(4)

系列1单回路直线塔回归关系式可以表示为：W=58 893+2.43fh-0.87fv；系列13双回路回归关系式可以表示为：W=46 739+0.93fh+0.21fv。使用上述2式拟合质量时，结果与真值平均误差不大于10.1%，95%置信区间下进行参数估计，可决系数R2非常接近1，关系式合理。多项式拟合非线性样本时，误差虽略大，但通用性很好。

2.4 铁塔质量计算关系式

综合式(3)铁塔质量与呼高的指数关系式和式(4)铁塔质量与荷载的线性关系式，得到质量计算关系式：

W=(β0+β1fh+β2fv)ebh

(5)

对于浙福线系列1单回路和系列13双回路直线塔施工图质量样本数据，采用回归分析方法，使用Matlab软件分析计算得到质量计算关系式见表2。

图3给出了采用表2计算关系式，由铁塔呼高和荷载计算系列1、系列13直线塔的质量与实际质量的对比情况，由图3可知，对系列1单回路直线塔各呼高的计算质量误差范围在7%以内，3%以内误差占54.2%，加权平均误差为3.4%；对系列13双回路直线塔各上相呼高的计算质量误差范围在5%以内，3%以内误差占70.5%，加权平均误差为2.4%。系列1计算误差大于系列13的主要原因在于前者覆冰厚度为15 mm，属中冰区，而后者为10 mm，属轻冰区，由于脱冰跳跃产生纵向不平衡张力的影响，使得前者15 mm中冰区计算精度略差，下面将研究重覆冰区铁塔质量计算关系式。

图2 单双回路直线塔质量与荷载的回归曲线

表2 单双回路直线塔质量关系式

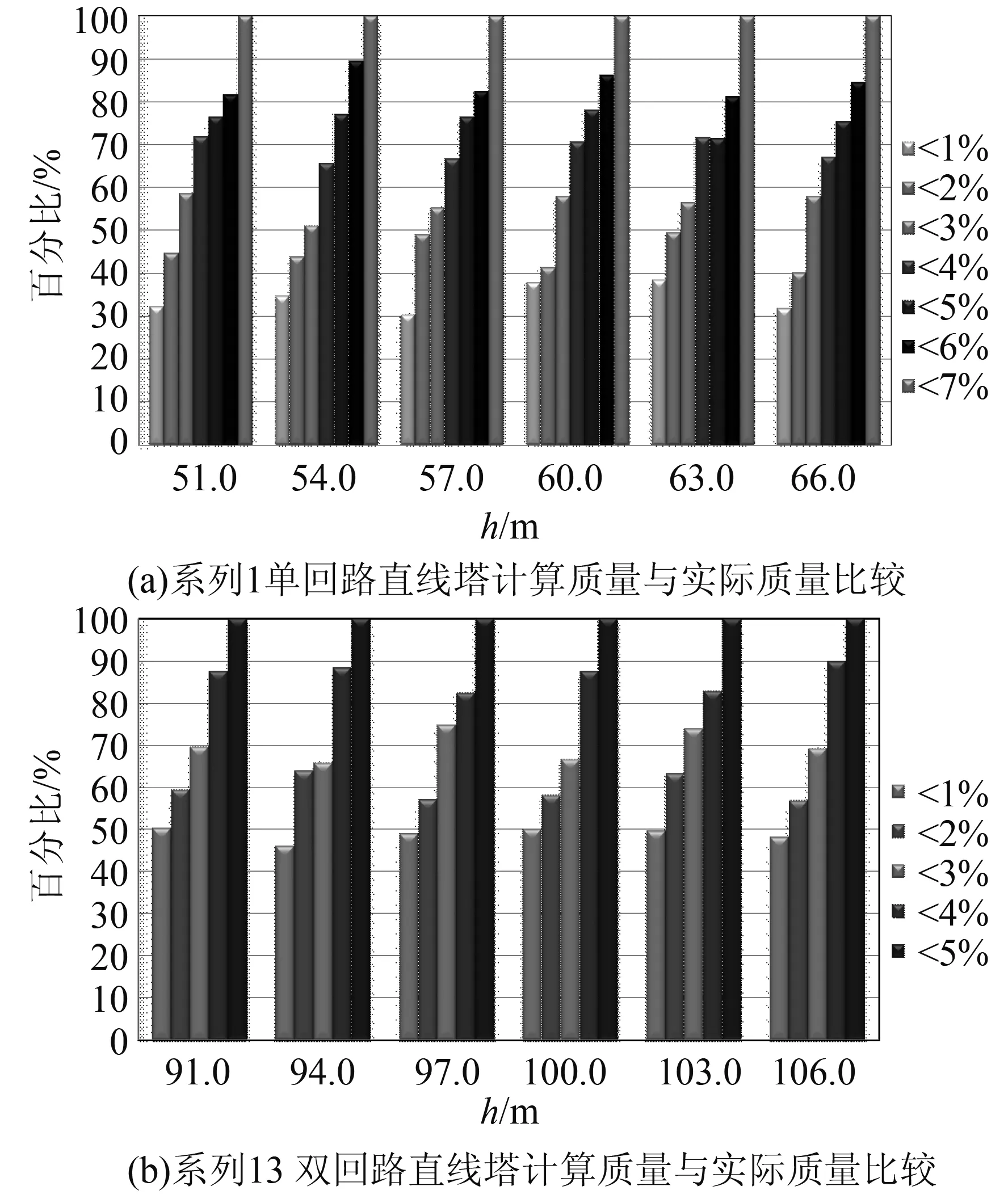
图3 单双回路直线塔计算质量与实际质量比较

2.5 重覆冰区铁塔质量计算关系式

重覆冰区包括中冰区和重冰区，即覆冰厚度大于10 mm的地区[15]。重覆冰区特高压线路，导线截面大，分裂根数多，覆冰重量大，脱冰跳跃产生的不平衡张力更大，由此产生垂直于铁塔横担方向的纵向荷载ft对直线塔质量影响很大，其质量计算模型关系式为

W=(β0+β1fh+β2fv+β3ft)ebh

(6)

浙福线重冰区线路均在山区，由于山区施工困难，只能采用单回路角钢塔，无法采用双回路钢管塔，因此根据重覆冰区线路相关设计规范[15]中不平衡张力取值，给出中、重冰区单回路直线塔质量计算关系式见表3。

图4给出了在考虑和不考虑不平衡张力纵向荷载ft下，推算10 mm轻冰区至30 mm重冰区直线塔质量与实际质量对比的误差情况。由图4可见，由10 mm轻冰区至30 mm重冰区，不平衡张力对铁塔质量的影响越来越大，绝对误差范围和加权平均误差明显增加。因此，10 mm轻冰区无影响，15 mm以上中、重冰区需考虑不平衡张力计算铁塔质量。

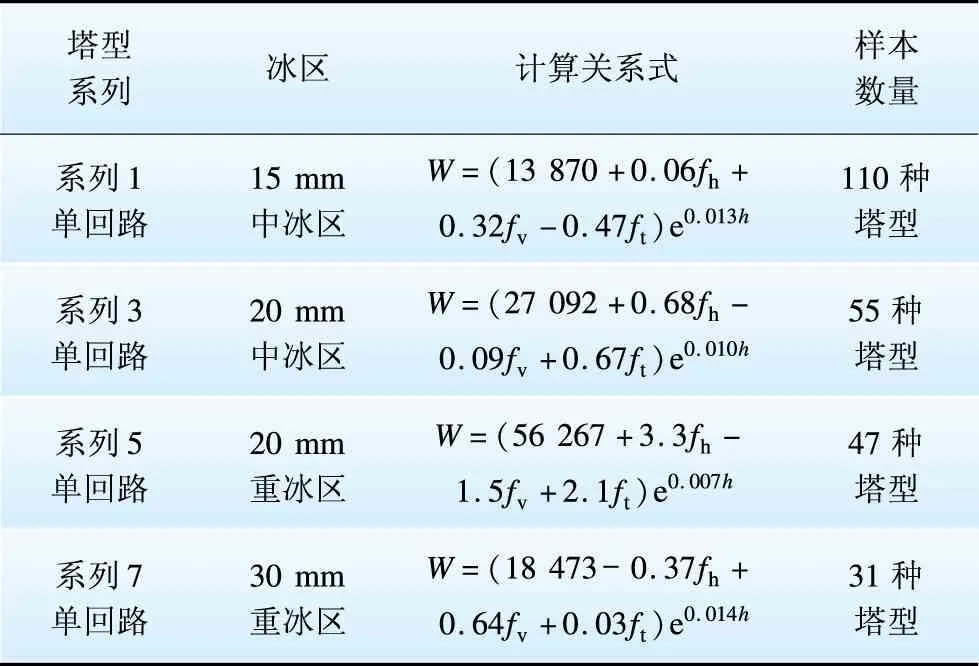
表3 重覆冰区直线塔质量计算关系式

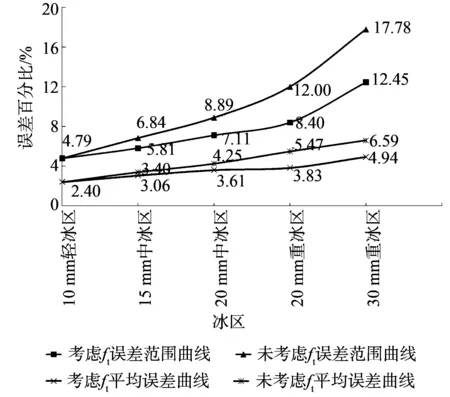
图4 重覆冰区计算误差对比曲线

2.6 转角塔(耐张塔)质量计算关系式

本文中转角塔主要是指耐张塔，由于转角塔的角度力可分解成水平荷载增加fh和垂直纵向荷载增加ft，因此转角角度力对铁塔质量影响很大[1-2]，其质量计算关系式仍可表示为式(6)。重覆冰区转角塔(耐张塔)不平衡张力按照重覆冰区线路相关设计规范[15]取值，并加入纵向荷载ft进行计算；由于不平衡张力远小于角度力，因此其对铁塔质量的影响较小。转角塔质量计算关系式见表4。

表4 转角塔质量计算关系式

图5给出了由转角塔呼高和荷载计算系列1、系列13转角塔质量与实际质量的对比情况。由图5可见，对系列1转角塔各呼高的计算质量误差范围在8%以内，5%以内误差占75.6%，加权平均误差为3.1%；对系列13转角塔各上相呼高的计算质量误差范围在9%以内，5%以内误差占62.6%，加权平均误差为4.14%。

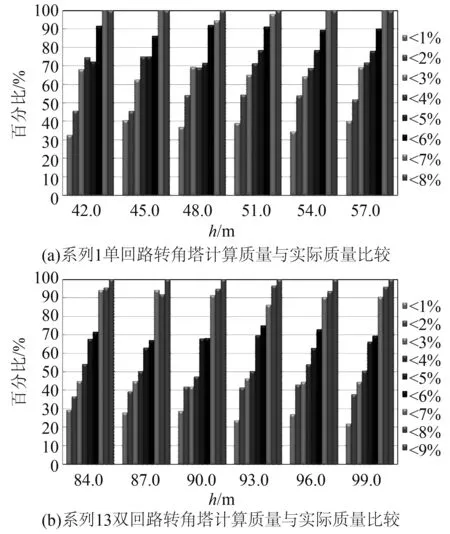
图5 单双回路转角塔计算质量与实际质量比较

3 500 kV输电线路铁塔质量计算分析

下面进一步检验回归分析关系式在计算500 kV超高压交流线路铁塔时的适用性。以“500 kV输电线路通用设计”[3]中子模块5E3为样本进行算例分析，5E3双回路设计条件：导线型号为4×JL/G1A-630/45，地线型号为2×JLB-150，设计最大风速为29 m/s，覆冰厚度为10 mm，海拔高度在1 000 m以下。该模块分平地和山区2个系列直线塔。平地悬垂串按V型布置，山区悬垂串按I型布置，转角塔采用20°分档的4塔方案，4型塔档位取60°～90°。采用式(5)和(6)分别对模块直线塔和转角塔的样本数据进行分析计算，得到质量计算关系式见表5。

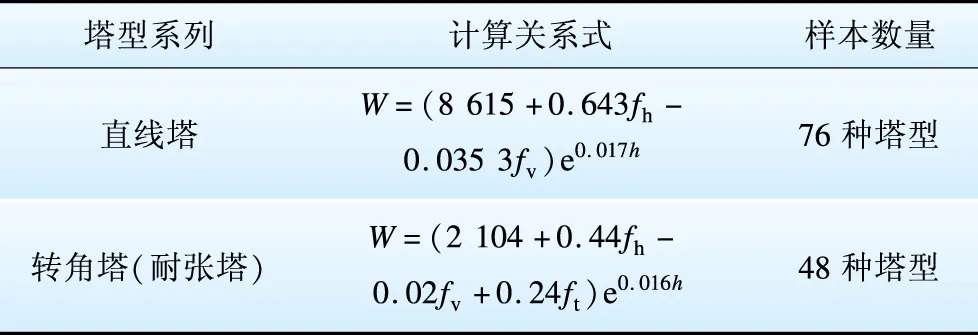
表5 5E3模块质量计算关系式

图6给出了采用表5计算关系式，由呼高和荷载计算5E3模块铁塔质量与通用设计质量对比的情况。由图6可见，对于双回直线塔各上相呼高，2层间距和取23 m时，计算质量误差范围在5%以内，3%以内误差占81.1%，加权平均误差为2.0%；双回转角塔各上相呼高，2层间距和取22.5 m，计算质量误差范围在7%以内，5%以内误差占85.9%，加权平均误差为3.1%。可见，回归分析关系式也可推广用于计算500 kV交流线路的铁塔质量。

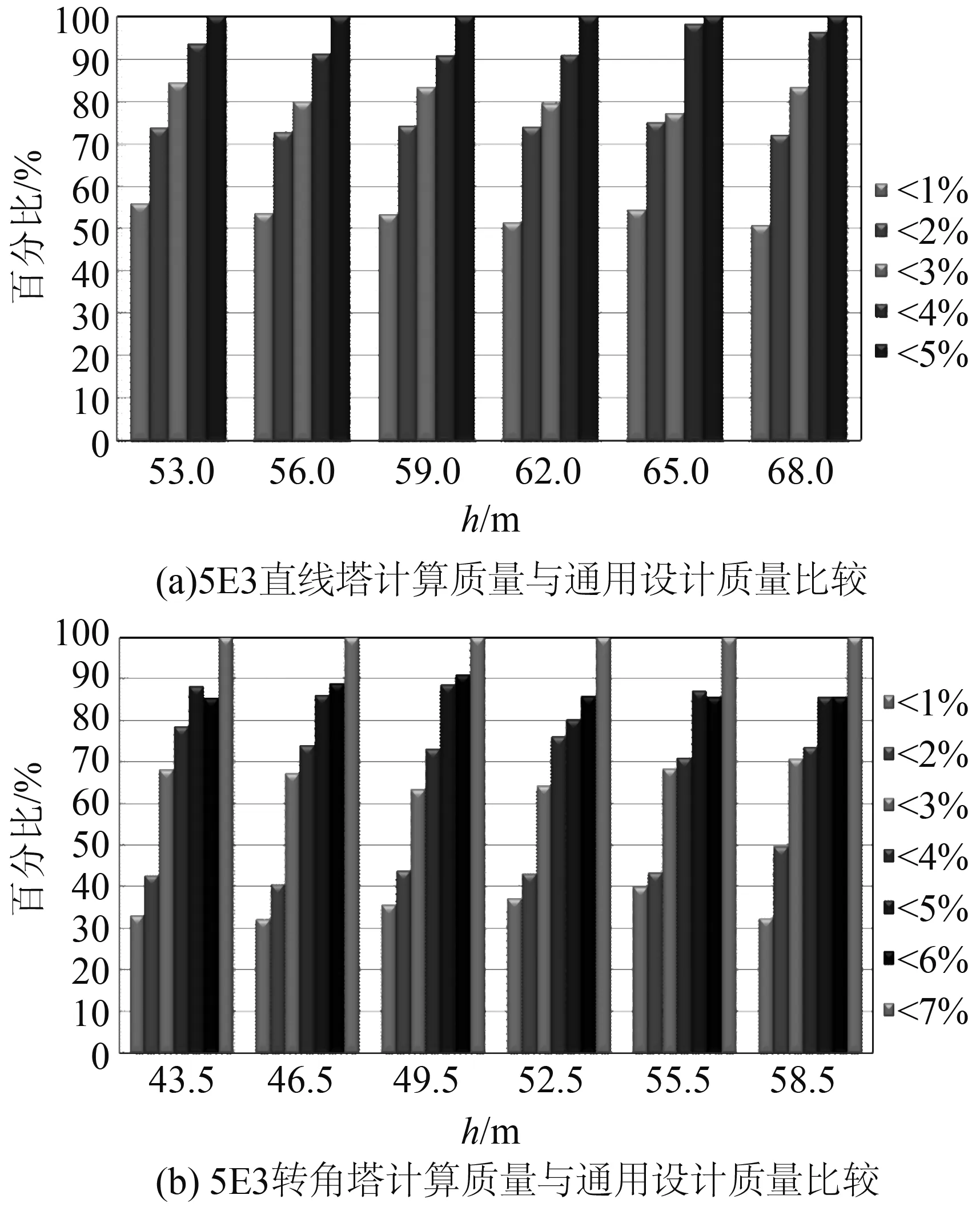
图6 5E3模块铁塔计算质量与通用设计质量比较

4 结 论

本文以“浙福线实际施工图”及“500 kV铁塔通用设计”为依托，采用回归分析方法，借助Matlab软件分析铁塔质量与呼高、荷载等变量之间的规律性；根据不同导地线、气象区(包括重覆冰区)、地形、海拔高度、单双回路、塔头布置的各种塔型质量数据样本，整理归纳出质量计算关系式，并将计算结果与实际质量进行比较，其误差小，精度高。

除呼高和荷载等主要因素外，影响铁塔质量的其他设计因素还包括：山地用长短腿与平丘用平腿、塔脚板与插入式连接方式、 kV值、串型、绝缘配置决定的不同串长、海拔高度引起的不同间隙值、电磁环境决定的不同导线相间尺寸等。长短腿与平腿、间隙值对铁塔质量略有影响，其他因素或影响很小，或不作为控制因素，均可忽略不计。采用计算关系式，由设计条件通过计算铁塔呼高和荷载来计算铁塔质量，简便实用，准确度较高，值得进一步推广应用。

[1]肖洪伟，肖兵，李力，等.输电线路铁塔设计荷载与质量的关系式分析[J].电力建设，2006，27(9)：4-6.

[2]林清海，杨博，陈鹏，等.基于非线性回归分析的特高压直流线路铁塔质量计算[J].电力建设，2013，34(5)：35-39.

[3]刘振亚.国家电网公司输变电工程通用设计500 kV输电线路分册[M].北京：中国电力出版社，2011.

[4]龙永红.概率论与数理统计[M].北京：高等教育出版社，2004：215-267.

[5]Madsen K，Nielsen H B，Tingleff O，et al.Methods for non-linear least squares problems[R]. Denmark：Technical University of Denmark，2004.

[6]徐萃薇，孙绳武.计算方法引论[M].北京：高等教育出版社，2002：62-85.

[7]张德丰.MATLAB概率与数理统计分析[M].北京：机械工业出版社，2010：233-260.

[8]唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现代化，2008，154(6)：15-19.

[9]Mathews J H，Fink K D.数值方法(MATLAB版)[M].北京：电子工业出版社，2005：195-215.

[10]苏金明，张莲花，刘波，等. MATLAB工具箱应用[M].北京：电子工业出版社，2004：489-512.

[11]孙昕，于刚，梁政平，等.GB 50665—2011 1 000 kV架空输电线路设计规范[S].北京：中国计划出版社，2011：23-30[12]于刚，梁政平，张鹏飞，等.GB 50545—2010 110 kV～750 kV架空输电线路设计规范[S].北京：中国计划出版社，2010：27-30.

[13]张殿生，倪宗德，张洞明，等.电力工程高压送电线路设计手册[M].北京：中国电力出版社，1999：166-206.

[14]邵天晓.架空送电线路的电线力学计算[M].2版.北京：中国电力出版社，2003.

[15]于刚，梁政平，王永刚，等.DL/T 5440—2009 重覆冰架空输电线路设计技术规程[S].北京：中国电力出版社，2009：20-21.

(编辑：张媛媛)

TowerWeightCalculationforUHVACTransmissionLine

YANG Bo1，LI Taobo1，YANG Maoting2，WANG Aihua1，MA Fang1

(1. Shandong Electric Power Engineering Consulting Institute Co., Ltd., Jinan 250013, China;2. Shandong University of Technology, Zibo 255049, Shandong Province, China)

At the stage of feasibility study and preliminary design for a new construction, tower weight can be correctly calculated under new design conditions, which may contribute to tower type selection and planning, path scheme comparison, optimum pole position and so on; it is significant for increasing the accuracy of financial estimation and decreasing construction cost. Therefore, on the basis of the calculation and analysis of tower weight in UHV DC transmission line, this paper intensively studied the tower weight in UHV AC transmission line which had heavier load and varied tower head forms, as well as the tower weight in 500 kV EHV transmission line. Taking the towers with different types and weights in “1 000 kV Zhefu transmission line” and “500 kV tower universal design” as the data sample, the mathematical model based on regression analysis was established, and the mathematical relationship were obtained in simulation software Matlab. The accuracy and feasibility of this method was validated through the comparison between calculation results and actual weight. As for medium & heavy icing areas, the calculation formulas should be revised and complemented by considering the influence of unbalanced tension of ice-shedding.

UHV AC; EHV; regression analysis; tower weight; load; heavy icing areas

TM 753

： A

： 1000-7229(2014)06-0106-06

10.3969/j.issn.1000-7229.2014.06.020

2014-02-20

：2014-03-21

杨博(1980)，男，硕士，工程师，主要从事架空输电线路的设计和研究工作，E-mail：yangbo@sdepci.com；

李陶波(1984)，男，硕士，工程师，主要从事架空输电线路的设计和研究工作，E-mail：litaobo@sdepci.com.cn。