双馈风力发电机组对电力系统稳定性的影响

武小梅，文福拴，刘国祥，欧英龙

(1.华南理工大学电力学院，广州市 510641; 2.广东工业大学自动化学院，广州市 510006;3.浙江大学电气工程学院，杭州市 310027; 4.广东电网公司湛江供电局，广东省湛江市 524005)

双馈风力发电机组对电力系统稳定性的影响

武小梅1,2，文福拴3，刘国祥2，欧英龙4

(1.华南理工大学电力学院，广州市 510641; 2.广东工业大学自动化学院，广州市 510006;3.浙江大学电气工程学院，杭州市 310027; 4.广东电网公司湛江供电局，广东省湛江市 524005)

随着双馈感应风力发电机组(doubly-fed induction generators，DFIG)装机容量在电力系统中所占比重的不断增加,其与电力网络之间的相互影响日渐增大。采用DIgSILENT软件包对含有DFIG的电力系统的暂态稳定性进行了研究,并从Crowbar保护控制与电力网络之间相互影响的角度探讨了DFIG的Crowbar投切策略。首先研究了单台DFIG的稳定性,然后以IEEE 30节点系统为例分析了在系统的同一节点分别接入DFIG型风电场和同步发电机组时系统的暂态稳定性;最后,从电力系统功角稳定性角度研究了Crowbar的最佳退出时间。结果表明,含DFIG型风电场的电力系统因短路电流降低使得继电保护范围缩小。

双馈感应发电机； 暂态稳定；Crowbar；DIgSILENT软件包

0 引 言

风力发电是最有前途的绿色能源之一,随着双馈感应风力发电机(doubly-fed induction generator, DFIG)装机容量在电力系统中所占比重的逐步增长,其与电力网络之间的相互影响趋于增大。因此,大型风电场(如 MW级双馈型风电场)对电力系统稳定性的影响不容忽视。DFIG由于具有有功功率和无功功率独立调节、励磁变频器所需容量小等优点,在风力发电系统中得到广泛应用。目前，针对DFIG自身抵御电压扰动能力较弱,实现低电压穿越比较困难的缺点,广泛采用了Crowbar硬件保护电路来保证DFIG的故障穿越能力。文献[1]采用PSCAD验证了Crowbar电路能够提高DFIG的低电压穿越能力。文献[2]从DFIG功角动态行为角度分析其对系统稳定性的影响。文献[3]认为与传统鼠笼式风力发电机相比,DFIG具有更好的暂态稳定性。文献[4]以美国西部电网WSCC 3机9节点简化系统为例, 研究了在某些特定故障条件下,双馈型风电场并网后对电力系统暂态稳定性产生的影响。文献[5]提出通过计算特征值对惯性常数的灵敏度,来判断DFIG对系统影响的性质。文献[6]用时域仿真法证实DFIG和常规同步发电机组并列后,再经远距离输电线接入大系统后不会恶化系统稳定性。文献[7]采用Matlab对交流励磁风力发电机组的稳定性做了仿真分析,结果表明DFIG风电场能改善电力系统稳定性。文献[8]以新英格兰39节点系统为例,考察了DFIG高渗透功率比例(40%)对电力系统暂态稳定和频率稳定的影响,研究表明:当故障发生在离风电接入点较近位置时,由于DFIG的Crowbar动作,风电在有功功率大量减少的同时吸收大量无功功率,会对暂态稳定性产生不利影响；当故障发生在离同步电机较近位置时,暂态稳定性有所改善。现有文献的研究表明,在双馈机组对电力系统稳定性影响方面尚没有一致的结论,原因在于不同文献所采用的双馈机组数学模型、参数不同,控制策略和控制参数也有差异。但是,这些文献都反映了系统总机械惯性降低和频率响应变差的问题。

本文从DFIG自身稳定性出发研究其对同步发电机组的影响,并且以IEEE30节点系统为例,研究了DFIG对电力系统暂态稳定和频率稳定的影响,最后从功角稳定的角度考察了Crowbar的最佳退出时间。

1 双馈风力发电机暂态模型及控制策略

在国内外现有的风电并网运行导则中,多数要求风电机组必须具备低电压穿越 (low voltage ride through, LVRT)能力。Crowbar保护电路退出时间对双馈风电机组的LVRT能力有很大的影响[9-12]。文献[9-11]都是针对单台DFIG的暂态响应来分析Crowbar的退出时间的。文献[9]指出Crowbar电路投入时间不应太长;文献[10-11]则指出Crowbar在短路故障切除之前退出运行,且退出运行的时刻尽可能接近短路故障切除时刻;文献[12]建议Crowbar投入后应在故障清除后1～2个周波内切除;文献[13]则提出采用无功判定法检测短路故障切除时间,实现故障切除后立刻退出Crowbar电路的策略。

假定定子和转子三相绕组对称且不考虑0轴分量, 则旋转d-q坐标系下DFIG的数学模型可作如下描述[14]。

磁链方程:

ψsd=Lsisd+Lmird

(1)

ψsq=Lsisq+Lmirq

(2)

ψrd=Lrird+Lmisd

(3)

ψrq=Lrirq+Lmisq

(4)

式中:ψ、i、L为绕组的磁链、电流、电感;下角标s表示定子,r表示转子，m表示互感。

电压方程:

(5)

(6)

(7)

(8)

式中:U为绕组的电压；s为电机的转差率；ω为坐标系旋转角速度；Rs、Rr分别为定、转子的电阻。

电磁转矩方程和运动方程:

Te=npLm(isqird-isdirq)

(9)

(10)

式中:Te为电磁转矩;np为电机的极对数;ωr为转子旋转角速度;TL为风力机提供的驱动转矩;J为风力机的转动惯量。定子有功功率和无功功率分别为

(11)

(12)

DFIG的变流器控制系统用于实现转子侧变流器控制和系统侧变流器控制。DFIG的变流器通常采用双环双PI控制，转子侧变流器的功率外环生成快速电流内环控制的电流参考值(d轴、q轴分量),电流内环控制转子电流,以实现有功功率和无功功率的控制。系统侧的变流器控制也采用双环双PI控制,直流电压外环同样产生其电流内环控制所需的电流参考值,而内环电流控制的d轴分量可实现转子与系统的无功交换控制,q轴分量可控制直流电压环节的电压处于设定值附近。

2 双馈风力发电机稳定性分析

DFIG稳定性指单台DFIG机组接入无穷大系统时的稳定性问题。DFIG异步运行,其转子转速可以通过改变交流励磁电源的频率进行调节,具有广泛的稳定运行范围,其在任一滑差的运行点上具有与传统同步发电机相同的功角特性方程[15]：

(13)

式中:E为发电机内电势,U为无穷大母线电压,XΣ为E到U的转移电抗。同步发电机的摇摆方程为关于功角的非线性二阶微分方程:

(14)

式中:T为发电机组的惯性时间常数;D为阻尼系数;PT为原动机输出的机械功率。DFIG由于机电解耦, 其转子运动方程是关于转速的一阶微分方程：

(15)

式中:Pw为风力机输出机械功率;ωg为风机的角速度。由于DFIG的功角和转速不存在积分关系,即 dδ/dt≠ωg,故不存在类似于同步发电机的动力学失稳问题。但是,由于DFIG采用了双闭环励磁调节,再加上DFIG的广义Park方程是非线性高阶微分方程[16],因此，存在电磁暂态下的动力学稳定性问题。

为了说明上述观点,在DIgSILENT软件中搭建2 MW DFIG接于无穷大系统的模型, 并经0.69 kV/20 kV和20 kV/110 kV 2台升压变压器接入110 kV无穷大系统,如图1所示。

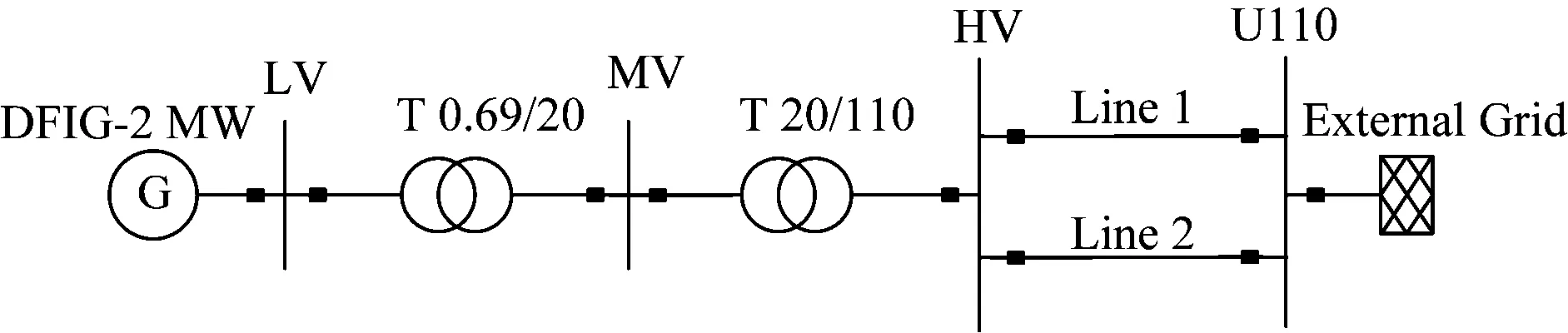
图1 接入DFIG的单机无穷大系统

双馈发电机参数如下:极对数np=2;额定有功容量和额定无功容量分别为2 MW和0.25 Mvar;定子额定电压为0.69 kV;额定频率f=50 Hz；定子侧采用Δ接法,以发电机额定容量为基准，定子电阻为0.005 9 pu,定子漏抗为0.079 0 pu;转子侧采用Y接法,转子电阻为0.006 2 pu,转子漏抗为0.112 0 pu;互感电抗为3.9 pu。在t=2 s时Line2线路上发生三相短路故障,2.6 s 后故障清除且线路重合闸重合成功,故障发生时风速保持恒定。

图2是故障前后的DFIG定子有功功率和无功功率响应曲线。由图可知,故障导致定子有功功率和无功功率发生剧烈振荡,当故障清除后经过大约1.3 s 后定子有功功率和无功功率又恢复到初始值,系统最终恢复了稳定。由图3可知,遭受扰动后的DFIG在机械转矩不变的条件下,其转速发生大范围波动,但没有出现动力学失稳现象。

因此,DFIG自身没有机电暂态失稳现象,也不存在其与系统中的同步发电机之间失步问题。此外,研究发现,当DFIG的定、转子绕组的电阻减小时,电磁模式阻尼变小,可能出现电磁暂态失稳现象。

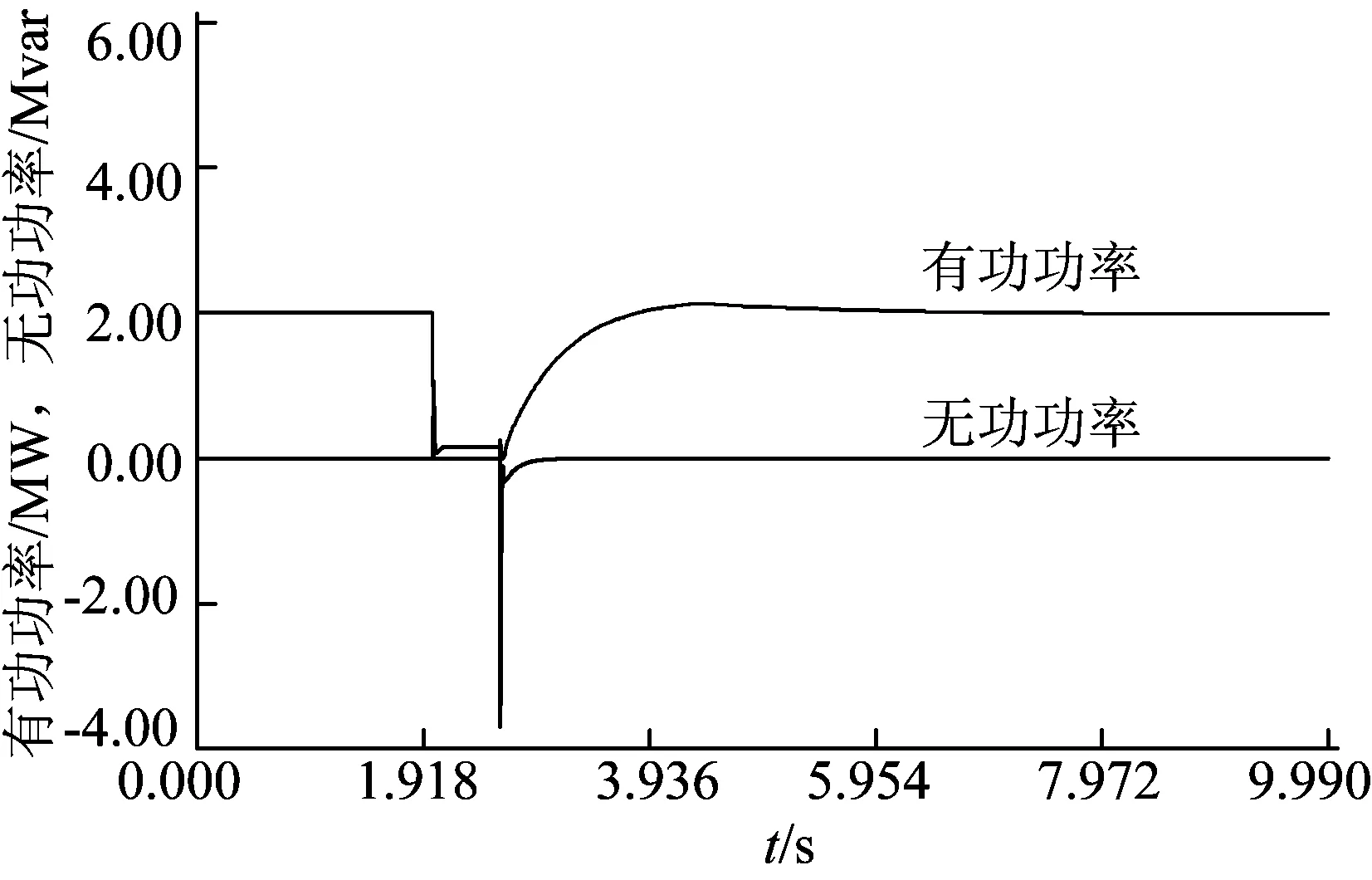
图2 DFIG定子有功功率和无功功率暂态响应波形

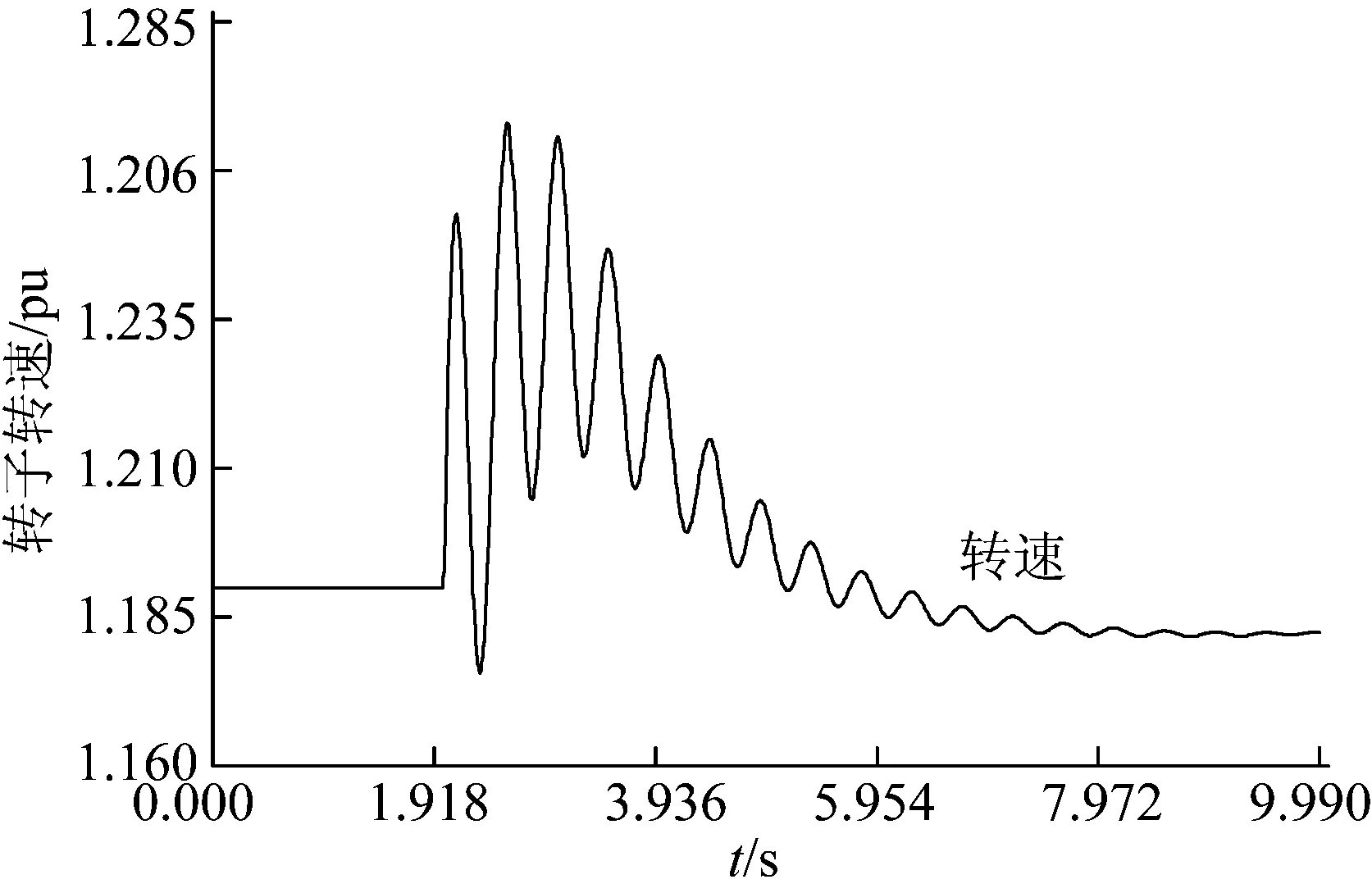
图3 DFIG转子转速的暂态响应波形

3 并列运行的DFIG对系统运行稳定性的影响

3.1 DFIG对系统短路容量的影响

电力系统暂态稳定是指系统遭受大扰动后,能从原来的运行状态不失同步地过渡到新的稳定运行状态的能力。风力发电机组作为一种电源,在系统发生短路故障后,也会向故障点输送短路电流。短路容量主要用来校验开关的切断能力,若断路器在短路时遮断容量不够,会引起断路器的爆炸。

图4为一个简单电力系统,在进行等值网络变换后,可求出系统的总阻抗XΣ*。当发生三相短路时,短路容量计算公式为

(16)

(17)

式中:Uav为短路处正常工作电压的平均值;IK为流过断路器的短路电流有效值；SB为基准功率；UB为基准电压。如果同步发电机组G2被风机替换,则从20 kV侧等效电路来看系统中总阻抗将变大,因为从风机出口电压0.69 kV折算到20 kV侧时其阻抗需乘以K2=(V20/V0.69)2,此时风机和相应的内部集电线路相当于一个很大的限流电抗,短路电流就会变小,因此断路器的遮断容量就需要重新整定。

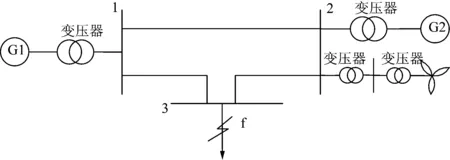
图4 简单电力系统的单线图

在DIgSILENT软件环境中搭建IEEE 30节点系统, 其参数及接线图见文献[17]。在IEEE 30节点系统中,发电机G1为平衡节点,假设该系统中G1、G2、G13分别为常规火电机组,系统的基准容量为100 MVA;G5、G8、G11分别接双馈型风电场,风电机组采用恒功率因数控制,定子出口额定电压为0.69 kV,其穿透功率为27.3%;系统中同步发电机模型采用计及交直轴次暂态电抗、交直轴暂态电抗的六阶模型,并考虑了励磁调节系统、调速系统的作用;负荷模型采用恒阻抗模型,负荷水平为283.4 MW。定义无风电接入的原系统为系统①，接入风电后为系统②,分别进行三相短路电流计算,结果如表1所示。

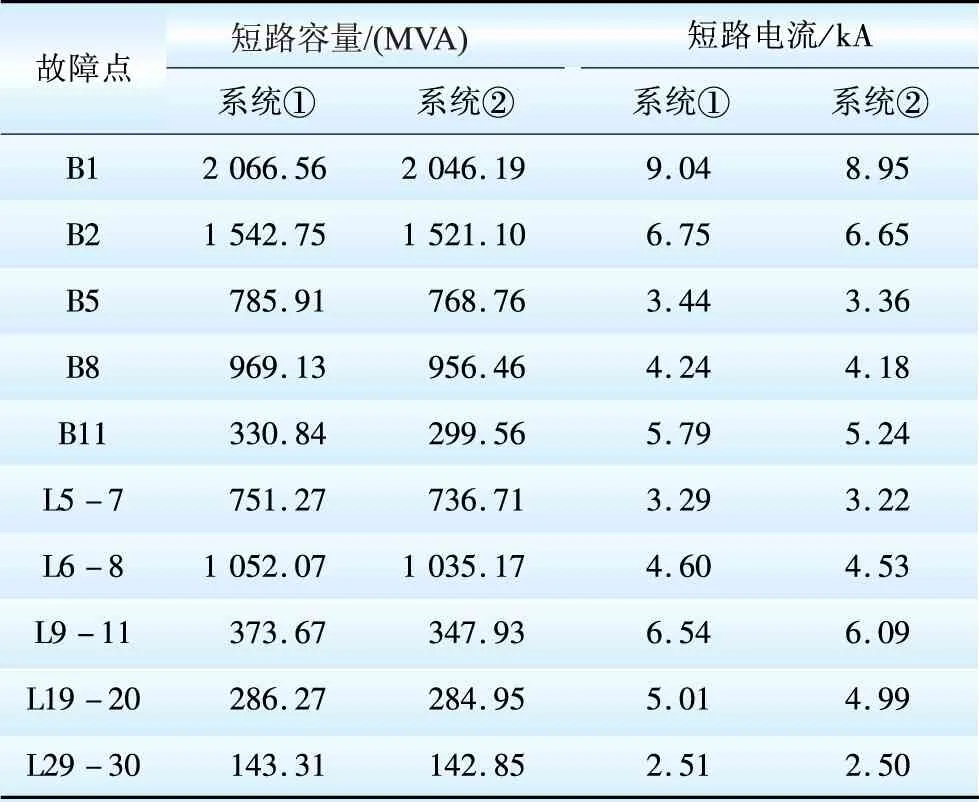
表1 2个系统发生三相短路时短路电流计算结果比较

从短路电流计算结果可知:系统接入风机后,短路容量和短路电流都降低,不会出现断路器在短路时遮断容量不足的问题,但是系统原来的保护定值已不能满足要求,所以需对系统原保护定值进行重新核算。如果按照之前设定的保护定值运行,则在系统发生短路后,由于线路上流过的短路电流随着大容量风电场的接入而减小很多,这使得保护范围缩小,这样线路上就会出现保护拒动,从而对电力系统稳定性产生不利影响。可以采用自适应继电保护解决风电引起的电网保护问题,因为这种保护能够根据系统运行方式和故障状态的变化而实时改变保护性能、特性或定值[18]。

3.2 DFIG对系统频率的影响

随着大量风力发电接入系统,对系统稳定性可能产生影响。可以从系统发生扰动和风电场发生扰动2个方面进行频率稳定性分析。对于系统发生扰动情形采用时域仿真法,针对IEEE 30节点系统①和系统②分析风电与系统之间的相互影响。

在仿真时,设置时间t=20 s时,同步发电机G13发生故障退出运行,假定仿真过程中风速不发生变化,仿真结果如图5、6所示。图5为系统频率响应特性曲线,图6为系统频率偏差曲线。

由图5、6的仿真结果可知,在系统发生有功功率缺额时,系统①和系统②的频率最后分别稳定在49.862 Hz和49.829 Hz,其频率偏差分别为-0.138 Hz和-0.171 Hz;在系统发生有功功率缺额而导致的频率下降过程中,同步发电机组能提供频率支持作用,即在其调速系统作用下能提供持续的有功出力,从而能够很好地维持频率稳定。对于DFIG而言,其控制系统使其发电机转速与系统频率完全解耦控制,在系统频率变化时,风电机组不能及时响应,因此会导致整个系统惯量降低,所以当系统中的双馈机组穿透功率较大,系统有功功率缺额较大时,不利于系统的频率稳定。

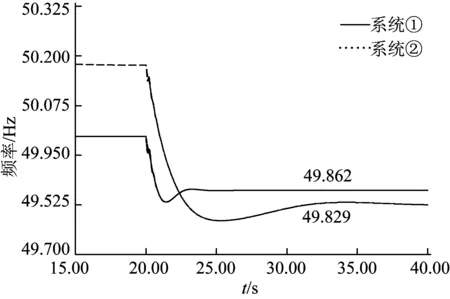
图5 系统频率响应特性曲线

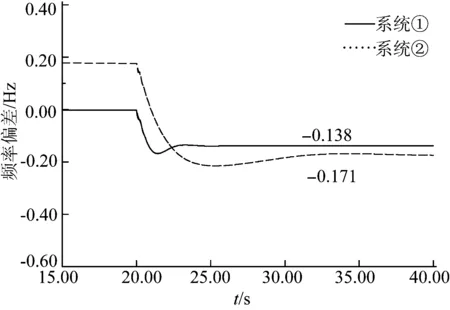
图6 系统频率偏差曲线

3.3 Crowbar保护退出时间对系统稳定的影响

低电压穿越能力是风电并网要求的核心内容之一,Crowbar保护是针对DFIG特别设计的,用来保护转子侧变流器,防止其出现过电流而损坏。当转子电流超出设定的阈值时,投入Crowbar电路,为转子过电流提供一条通道,即阻塞变流器以取得保护效果。

这里以IEEE 30节点系统②为例,从Crowbar的不同退出时间与系统的交互影响角度进行分析。给定8号母线在1 s时发生三相短路故障,1.3 s时故障切除; 故障发生后,8号母线所接DFIG的Crowbar保护电路立刻投入,这里分析Crowbar分别在下面3种工况下对同步发电机的功角特性、有功功率、励磁电压的影响:(1)故障发生时投入, 故障清除前切除;(2)故障发生时投入,故障清除后立即切除;(3)故障发生时投入,故障清除后继续运行一段时间再切除。下面分别给出系统频率曲线(图7)和G2的功角特性、有功功率、励磁电压的波动曲线(分别见图8、9、10)，及故障清除后Crowbar继续运行一段时间G2的功角特性波动曲线(图11)。

由图7～10可知, Crowbar在故障清除前切除和故障清除后立即切除这2种情况下其各曲线的波动情况基本一致, 且都比Crowbar在故障清除后继续运行一段时间再切除波动范围大。例如, 图7中Crowbar在故障清除前切除, 系统频率最后稳定在49.819 Hz; Crowbar在故障清除后立即退出, 系统频率最后稳定在49.822 Hz; 故障清除后继续运行一段时间再切除, 频率最后稳定在49.889 Hz。

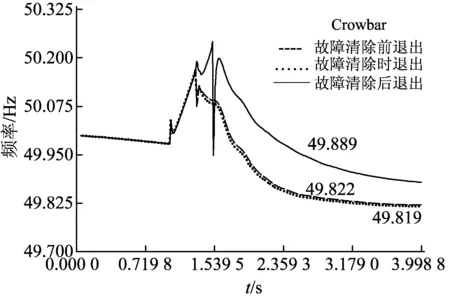
图7 在不同的Crowbar退出时间下频率响应特性曲线

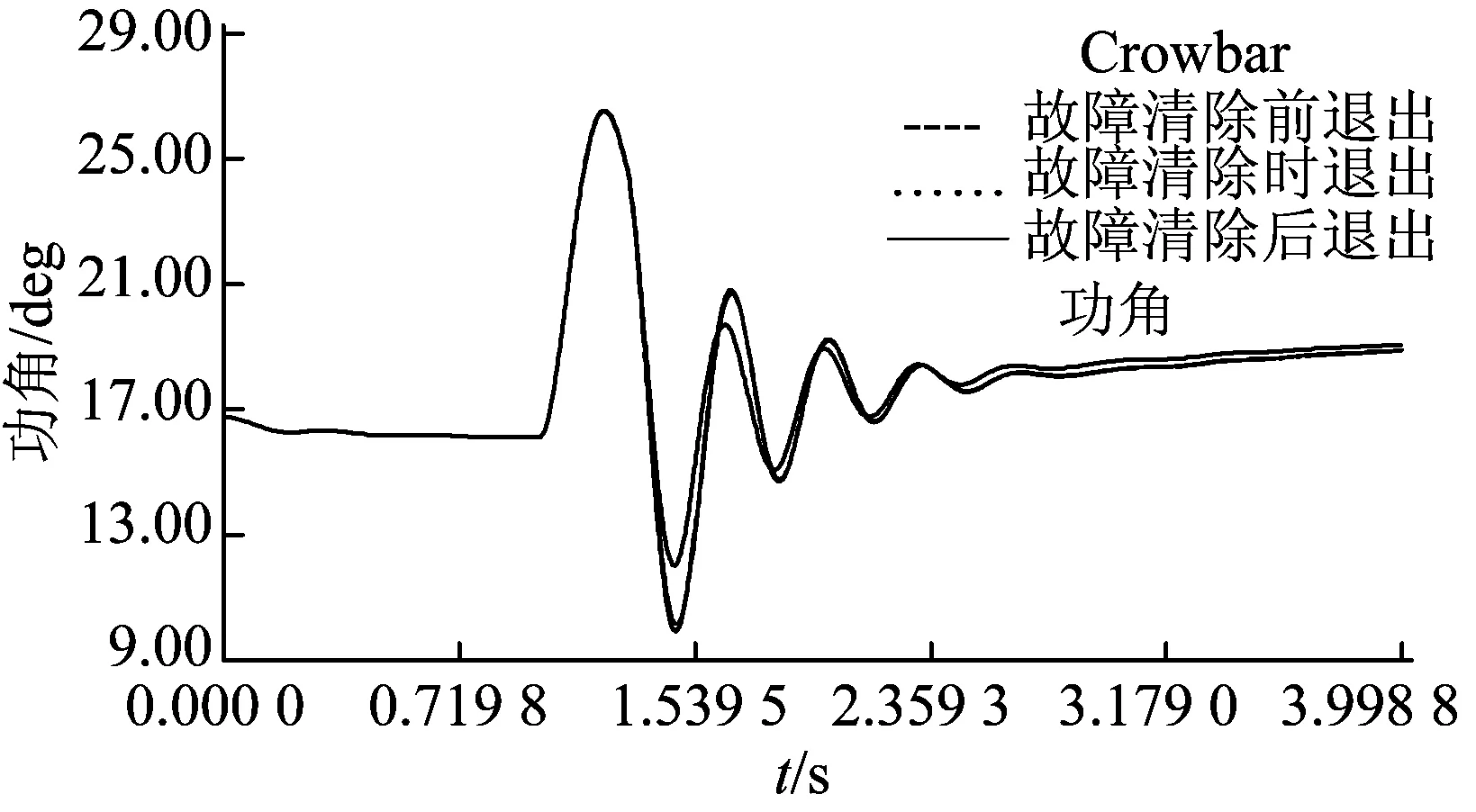
图8 在不同的Crowbar退出时间下G2的功角波动曲线

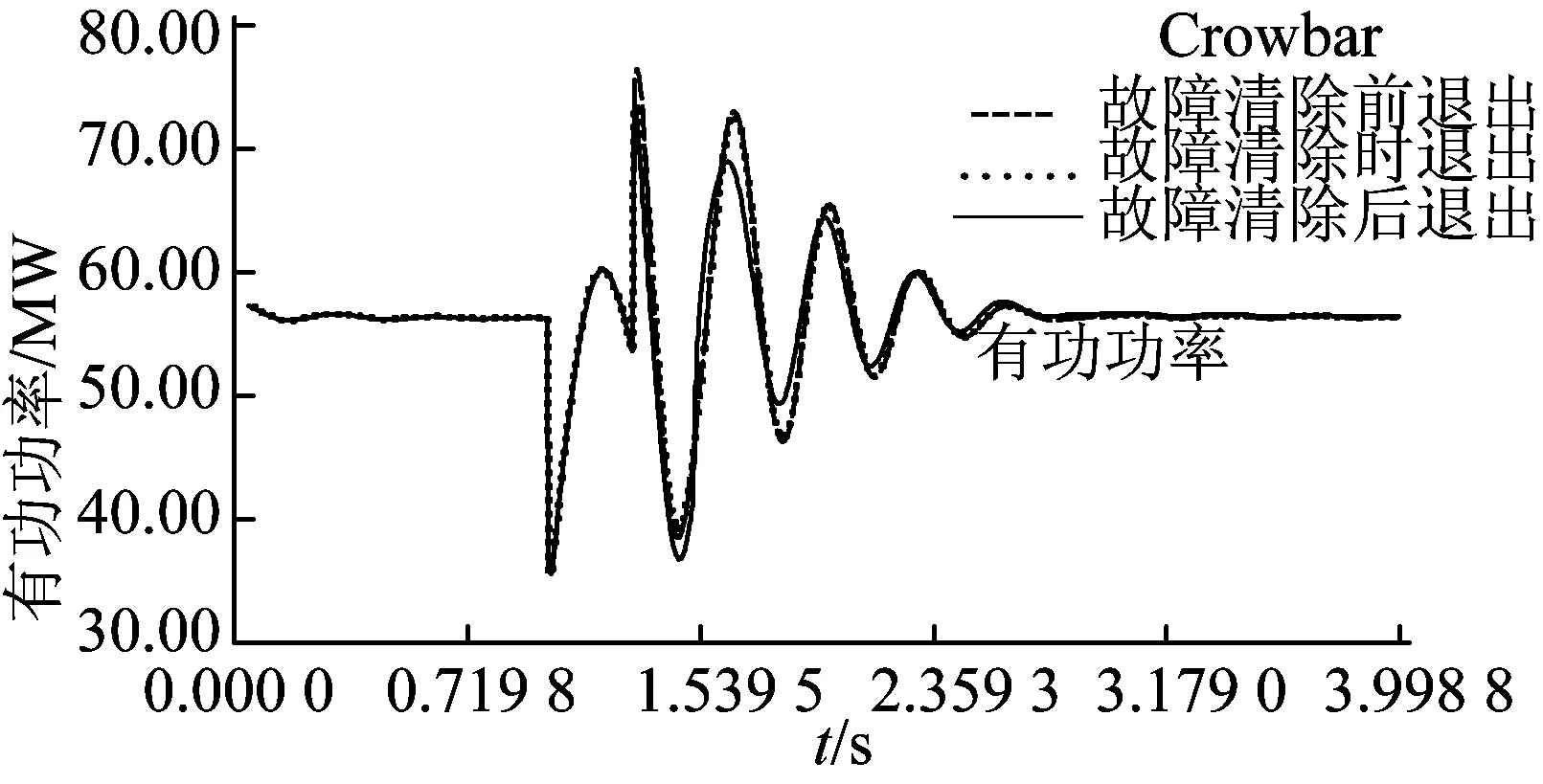
图9 在不同的Crowbar退出时间下G2的有功功率波动曲线

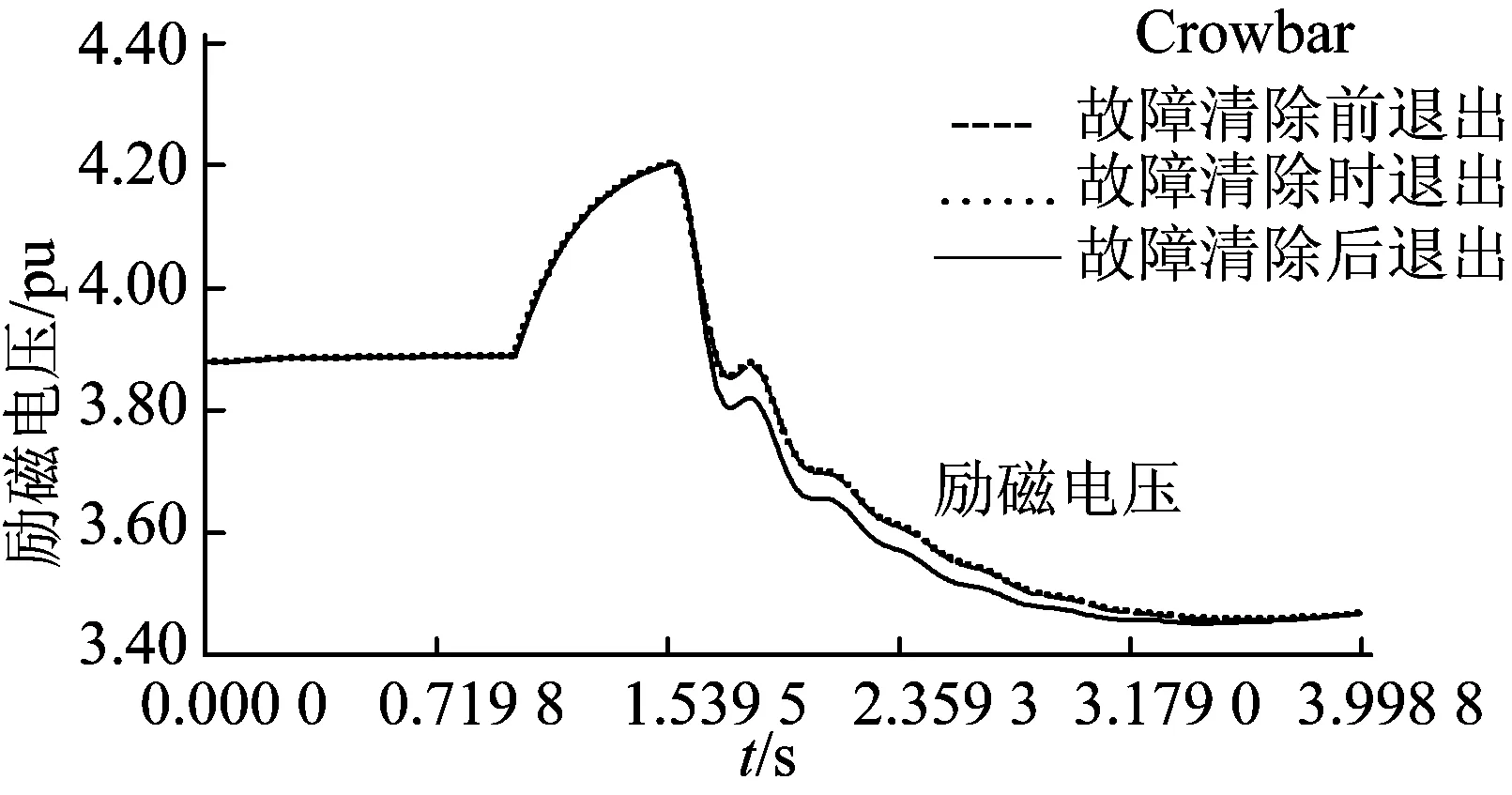
图10 在不同的Crowbar退出时间下G2的励磁电压波动曲线

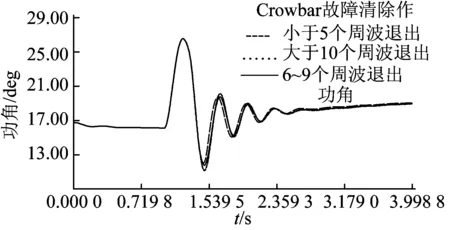
图11 故障后在不同的Crowbar退出时间情形下G2的功角波动曲线

由图8可知, Crowbar在故障清除后继续运行一段时间再切除时, 功角波动范围较小。由图11可知, Crowbar在故障清除后6～9个周波再切除时, 功角波动范围最小。

4 结 论

本文研究了DFIG对电力系统暂态稳定性、频率稳定性的影响以及Crowbar保护不同退出时间对系统稳定性的影响, 并以IEEE 30节点系统为例做了仿真分析, 得到如下结论:

(1)对于DFIG单机接无穷大系统, 仿真结果表明, DFIG自身没有机电暂态失稳现象, 也不存在DFIG与同步发电机的失步问题。

(2)含DFIG的电力系统短路电流计算结果表明, 由于DFIG引起短路电流减小, 从而使得继电保护范围缩小，线路上会出现保护装置拒动, 对系统稳定性产生不利影响。

(3)在DIgSILENT中建立了含有DFIG的30节点系统模型, 其中风电穿透功率达到27.3%。当系统中的DFIG穿透功率较大, 系统有功功率缺额较大时, 不利于系统的频率稳定。最后, 从功角稳定性角度验证了Crowbar在故障清除后继续运行6～9个周波再切除效果最佳。

[1]LIMA F K A. Rotor voltage dynamics in the doubly fed induction generator during grid faults[J]. IEEE Transactions on Power Electronics, 2010, 25(1), 118-130.

[2]郝正航, 余贻鑫. 双馈风力发电机组对电力系统稳定性影响[J].电力系统保护与控制, 2011, 39(3): 7-11.

[3]赵清声, 王志新. 双馈风力发电机组系统接入与稳定运行仿真[J]. 电网技术, 2007, 31(22): 69-74.

[4]石立宝, 戴世强. 大规模双馈型风电场并网的系统暂态稳定仿真[J]. 电力系统及其自动化学报, 2009,11(4): 1-6.

[5]Gautam D, Vittal V, Harbour T. Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems[J]. IEEE Trans on Power Systems, 2009, 24(3): 1426-1434.

[6]Muljadi E, Butterfield C P, Parsons B, et al. Effect of variable speed wind turbine generator on stability of a weak grid[J]. IEEE Trans on Energy Conversion, 2008, 22(1): 29-35.

[7]闫广新,吐尔逊,晁勤.交流励磁双馈风力发电机组的稳定性仿真分析[J].继电器,2007,35(14):7-9.

[8]Meega H L, Flynn D. Impact on transient and frequency stability for a power system at very high wind penetration[C]//IEEE Power and Energy Society General Meeting, Minneapolis:IEEE,2010: 1-6.

[9]姜传,肖湘宁.应用撬棒电路的双馈型风力发电机低电压穿越分析[J].电网与清洁能源,2012,28(1):80-83.

[10]张靠社,王媛,胡德海.基于Crowbar保护的双馈感应发电机组的低电压穿越研究[J].电网与清洁能源,2011,27(10): 66-70.

[11]朱晓东,石磊,陈宁,等.考虑Crowbar 阻值和退出时间的双馈风电机组低电压穿越[J].电力系统自动化,2010,34(18): 84-89.

[12]徐殿国,王伟,陈宁.基于撬棒保护的双馈电机风电场低电压穿越动态特性分析[J].中国电机工程学报,2010,30(22):29-36.

[13]李鸿儒,金炜东,胡立锦,等.基于无功判定法的Crowbar 保护电路退出控制[J].电力系统保护与控制,2012,40(15):99-103.

[14]贺益康,胡家兵,徐烈.并网双馈异步风力发电机运行控制[M].北京:中国电力出版社,2011.

[15]陈树勇,陈会员,唐晓骏,等.风火打捆外送系统暂态稳定切机控制[J].电网技术,2013,37(2):514-519.

[16]高景德,王祥珩,李发海.交流电机及其系统的分析[M].北京:清华大学出版社, 2005.

[17]刘明波,谢敏,赵维兴.大电网最优潮流计算[M].北京:科学出版社,2010.

[18]沈冰,何奔腾,张武军.新型自适应距离继电器[J].电力系统自动化,2007,31(7):39-44.

(编辑：张小飞)

ImpactofDoubly-FedInductionGeneratoronPowerSystemStability

WU Xiaomei1,2, WEN Fushuan3, LIU Guoxiang2, OU Yinglong4

(1. School of Electric Power, South China University of Technology, Guangzhou 510641, China;2. Faculty of Automation, Guangdong University of Technology, Guangzhou 510006, China;3. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China;4. Zhanjiang Power Supply Bureau, Guangdong Power Grid Corporation, Zhanjiang 524005, Guodong Province, China)

With continuous increase of installed capacity of doubly-fed induction generators (DFIG)in power systems, the interaction between DFIG and power system is becoming more significant. This paper studied the transient stability of power system containing DFIG with using software package DIgSILENT, and discussed the switching strategy of Crowbar for DFIGs through investigating the interactions between the Crowbar protection/control and the power system. First, the stability of a single DFIG was investigated. Then, taking IEEE 30-bus system as example, the transient stability of a scenario with a DFIG wind farm or a synchronous generator respectively connected to a same bus was analyzed. Finally, the optimal exit time of Crowbar was studied form the aspect of power angle stability. The results show that the short-circuit current of the power system containing DFIG wind farm is reduced, so the range of the protective relay can be decreased.

doubly-fed induction generator; transient stability; crowbar; software package DIgSILENT

国家高技术研究发展计划(863计划)资助项目(2011AA05A105)；广东省电力节能与新能源技术重点实验室资助项目(ZDSYS200701)；广东电网公司2012年科技项目(K-GD2012-218)。

TM 315

： A

： 1000-7229(2014)06-0007-06

10.3969/j.issn.1000-7229.2014.06.002

2013-12-14

：2014-03-21

武小梅 (1972), 女, 博士, 副教授, 主要研究方向为电力系统运行分析与控制以及新能源发电，E-mail: eexiaomei@126.com;

文福拴 (1965), 男, 特聘教授, 博士生导师, 主要研究方向为电力系统故障诊断与系统恢复、电力经济与电力市场、智能电网与电动汽车，E-mail: fushuan.wen@gmail.com。