微电网中分布式电源简化模型

马川，刘迎澍

(天津大学电气与自动化工程学院，天津市 300072)

微电网中分布式电源简化模型

马川，刘迎澍

(天津大学电气与自动化工程学院，天津市 300072)

基于当前微电网研究领域热点，在某些不考虑具体设备暂态过程的仿真研究中，为缩短建模时间和仿真时间，滤除仿真结果中的谐波干扰，针对分布式电源详细模型的本质特点，对其组成部分原动机和逆变器分别进行简化，提出相应的简化模型。在光伏并网的仿真场景下，建立整体仿真模型，将详细模型与简化模型进行对比可知：简化模型不仅在稳态时达到了与详细模型相同的结果，而且暂态响应优于详细模型，达到了预期的对简化模型的要求。

微电网；分布式电源；简化模型；光伏并网

0 引 言

当前环境问题日益加重，雾霾天气严重威胁着人们健康。雾霾产生的主要原因就是化石能源的使用消耗，包括煤的燃烧，汽车尾气等。清洁能源的使用可以大大减少对化石能源的依赖，减轻对环境的破坏，很长时间以来成为能源领域研究的重要课题。如今，利用可再生能源发电的技术日趋成熟，但是对可再生能源发出的电能进行安全可靠和有效的使用，仍是一个亟待解决的问题。可再生能源发电，包括光伏电池、风力发电等，具有对环境条件很强的依赖性，输出电能受环境条件影响很大，包括温度、光照、风速等等，造成了其输出电能的不稳定性和不可预测性。针对这个问题，微电网的概念被提出，随之众多学者对其进行了广泛的研究，目的在于解决分布式电源，主要是可再生能源的使用[1-2]。

微电网系统的仿真研究是微电网研究领域的一个重要方面，是实现验证微电网控制方式、实施能量管理策略、演算优化算法等目标的重要手段。文献[3-5]通过建立微电网中各组件的详细模型，对各种控制策略进行了仿真研究，得到微电网的暂态和稳态反应结果。在仿真过程中，模型的建立至关重要，影响到仿真过程的顺利进行以及结果的准确性与可靠性。一般来说，模型包括详细模型和简化模型。详细模型虽然反映了不同分布式电源具体的特点，包括稳态阶段和暂态阶段，但是详细模型不仅建模繁琐，仿真时间长，模型冗繁，易于出错，而且不同模块组合时需要考虑兼容性问题。重要的是，在不考虑具体设备暂态过程仿真研究时，由于微电网中大量电力电子设备的使用，大量谐波的引入影响了对仿真目标的实现和观测。文献[6]指出，分布式电源、电力电子变流装置及相应的控制器建模是微电网系统仿真研究必须面对的重要问题，但是在含大量分布式电源和电力电子变流装置的微电网系统仿真研究中，针对不同的研究目的和应用场合，并不是总需要对所有研究对象都采用详细模型。这时，在一定条件下建立的简化模型就可以满足系统仿真的需要。

本文在对分布式电源构成分析的基础上，分别建立其构成模块原动机和逆变器的简化模型，为了验证其可行性和优越性，在光伏并网的仿真环境下，将简化模型和详细模型作仿真对比。

1 分布式电源简化模型

1.1 分布式电源构成

微电网中的分布式电源可以分为两类：一类是基于同步发电机或是异步发电机的分布式电源，如微型燃气轮机等；另一类是基于逆变器功率变换接口的分布式电源，如光伏电池、燃料电池等等[7]。微电网中的储能装置如果采用逆变器接口，也可以将其归为第二类。本文研究的分布式电源为第二类，即逆变器接口型分布式电源。

逆变器接口型分布式电源包括2个部分：原动机部分和逆变器部分，示意图如图1所示。

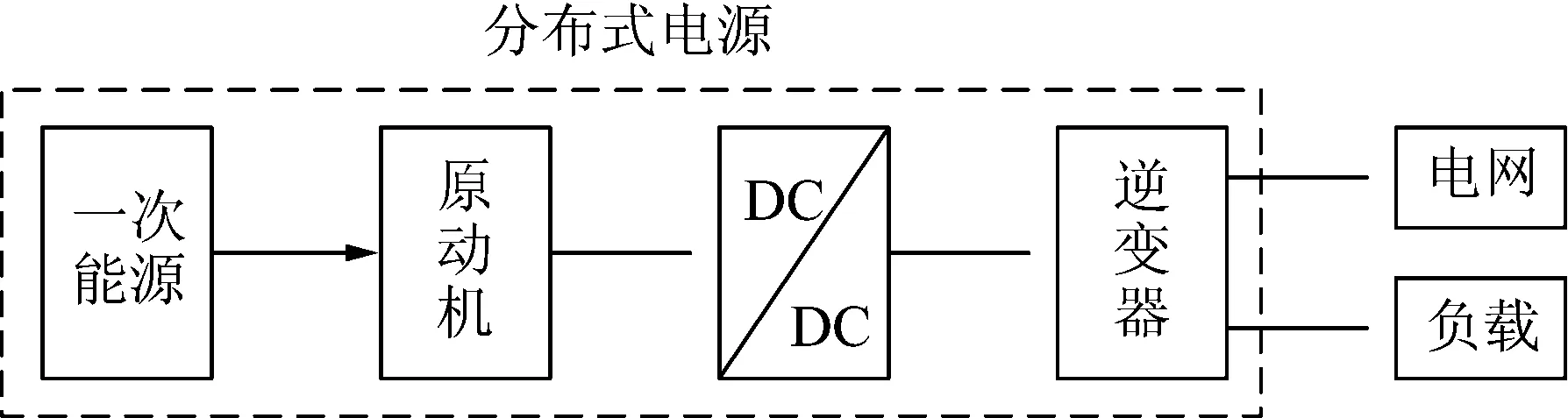
图1 分布式电源构成示意图

原动机部分的作用是将一次能源，如光能等，转化为二次能源，即电能，相应的应用实例为光伏电池等。原动机输出的电能不能够直接并网或是用于负载，还需要经过一系列的电力电子装置，最终变换成电压和功率为额定值的交流电。这里的电力电子变换装置包括DC/DC变换器和DC/AC变换器，前者一般为boost斩波电路，主要是由于原动机输出的直流电压较低，不能满足直流交流变换器对输入电压的要求，需要通过boost斩波电路升压。后者通常称为逆变器。本文研究分布式电源简化模型时，将DC/DC变换器和原动机视为同一部分，作用是为逆变器提供满足输入电压要求的直流电源，将逆变器视为另一独立部分，作用是将原动机部分输出的直流电变换为负载可用的交流电。

当研究电力系统问题时，相对于分布式电源的内部特性，研究人员更关心它们的外部输出特性，这是本文研究分布式电源简化模型的基础。本文建立的分布式电源简化模型也包括2个部分：原动机简化模型和逆变器简化模型。

1.2 原动机简化模型

1.2.1 原动机输出特性分析

在分析分布式电源特性以及研究微电网整体系统时，可以近似使用直流源代替原动机输出，即将直流源作为分布式电源的输出源。直流源包括电压源和电流源两种。传统微电网对分布式电源控制策略仿真研究时，逆变器直流侧通常接电压源，原因如下：

(1)一般地，微电网中分布式电源的直流侧会并联储能装置，这样其直流侧的电压基本保持恒定；

(2)经过逆变器逆变的分布式电源的原动机与逆变器之间的电容可以在暂态时提供系统所需要的电能，用以维持分布式电源的输出电压，起到功率缓冲作用，而且对于分布式电源来说，环境条件如光照、温度、风速等对其输出影响较大，在暂态反应的微小时间段内输出电压可以认为是不变的，其影响可以不予考虑。

然而，这里将电压源作为原动机的简化模型是有条件限制的，即原动机的输出侧需并联储能装置[8]，用以维持电压稳定，前提是在储能装置充放电允许范围内可弥补原动机产生功率和逆变器输出功率的差额，这对储能装置的容量也有一定的要求。多个小功率分布式电源组成微电网时，储能装置的配置对成本影响很大。同时在仿真实验过程中，电压源作为原动机不能反映分布式电源的功率源特性。

所谓功率源特性是指，在微电网系统中，分布式电源原动机在不同环境条件的影响下，可输出的最大功率是一定的，为了效率最大化，通过控制电力电子装置，使得分布式电源实时追踪最大功率点，获得最大功率输出，本质上原动机可以等效为一个功率源，即在环境条件不变的情况下输出功率为定值。

总结得出微电网中分布式电源逆变器直流侧原动机的输出特性:输出端电压稳定，无突变；输出功率可控。

分布式电源原动机简化模型建立的原则是功率等效原则，即简化模型模拟分布式电源的功率输出，任意时刻输出的功率与实际电源相等即可，忽略电能的具体产生过程和接口直流功率变换器的变流过程。

1.2.2 原动机简化模型

基于分布式电源原动机最大功率输出的功率源输出特性，原动机简化模型建立的原则为功率等效原则，即简化模型模拟原动机的功率输出，任意时刻输出的功率与实际电源相等即可，忽略电能的具体产生过程和电源接口变换器的功率变换过程。

若要电压源满足功率源特性须改变输出端电压从而改变输出功率，而一般的逆变器要求直流侧电压稳定，故电压源不适合。本文提出基于受控电流源作为原动机输出源的简化模型，示意图如图2所示。

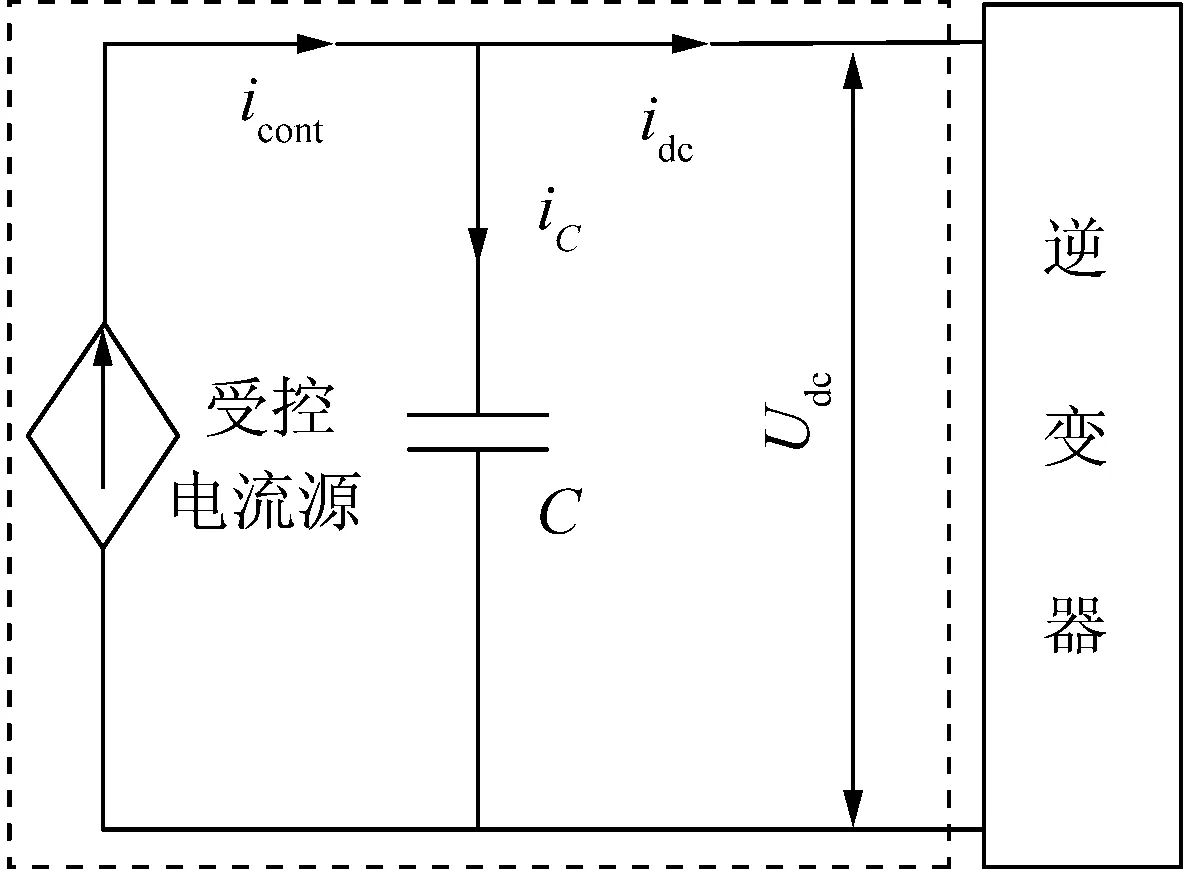
图2 原动机简化模型示意图

图中，虚线框内部分为原动机简化模型，该简化模型由一个受控电流源和一个稳压电容组成。其中，受控电流源根据反馈控制环节控制输出电流从而控制输出功率在指定值，电容的作用是稳定输出端电压，使其不发生突变。

受控电流源通过改变输出电流icont来改变输出功率，若原动机简化模型输出小于指定值，icont增加，假定此时输出侧电流idc不变，电容上流过电流iC，输出端直流电压Udc增加，导致idc增大，原动机简化模型增大到指定值；反之亦然。

这样，本文提出的原动机简化模型完全可以满足前文所分析的原动机输出特性，即输出电压稳定，无突变且输出功率可控。

1.2.3 原动机简化模型控制

图2中原动机简化模型输出功率为

Pdc=Udcidc

(1)

根据节点电流方程，有：

icont=idc+iC

(2)

替换idc，有：

(3)

式中：Pdc为控制输出功率；icont为控制输入电流；Udc为扰动输入电压。

根据上述动态方程构建控制系统动态结构图如图3所示[9]。

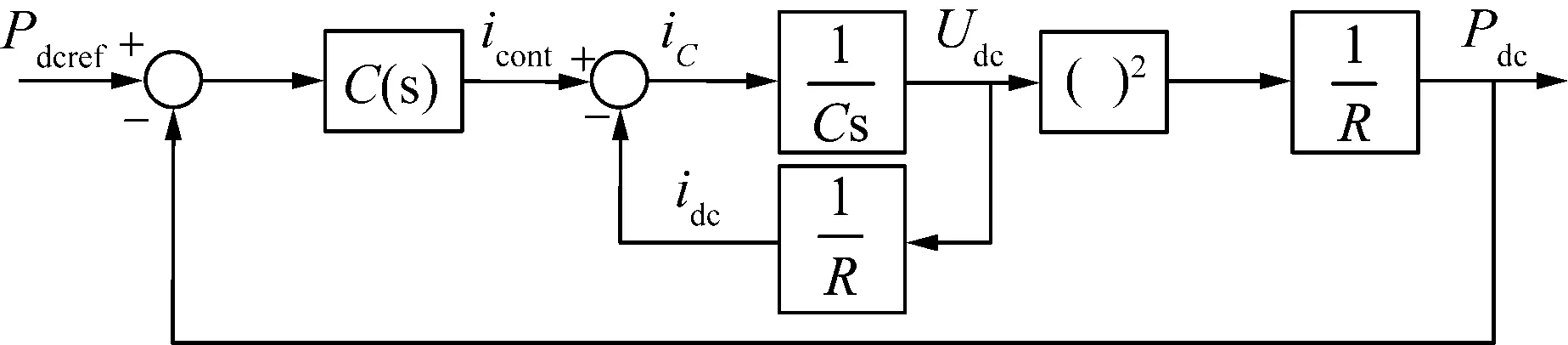
图3 原动机简化模型控制系统动态结构图

这里，逆变器的输入阻抗简化为电阻R表示。控制补偿器C(s)参数可以根据系统开环传递函数在时域和频域整定，这里不展开讨论。

1.3 逆变器简化模型

分布式电源逆变器的作用是将原动机产生的直流电变换成负载可用的交流电。通常其详细模型采用三相桥式电路，如图4所示。

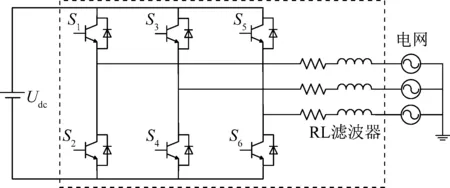
图4 逆变器详细模型电路图

上图中虚线框内为逆变器详细模型电路，由3组桥式开关管反并联二极管组成，输出侧接RL滤波器。开关管由SPWM控制产生的开关信号控制通断，将输入侧直流电逆变成交流电，输入电网或供给负载。

由开关电路构成的逆变器详细模型在仿真过程中，不仅减小了仿真步长，增加了仿真时间，而且引入大量的开关谐波，此时，需要构建逆变器的简化模型取而代之。由于三相逆变器可以由3个单相逆变器组成，为了简化讨论，本文以单相为例说明简化过程。

首先建立逆变器基于开关函数的数学模型。单相半桥逆变电路如图5所示[10]。

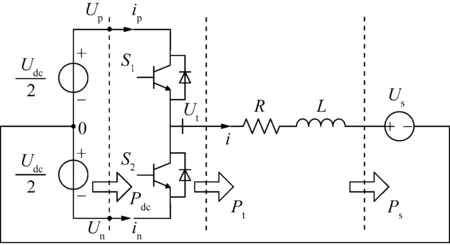
图5 单相半桥逆变电路图

图中，选择直流电压中点为零点电压，那么：

(4)

开关管开关函数定义如下

(5)

而且：

(6)

逆变器输出侧电压：

(7)

这里将逆变单路作理想化处理，即不考虑线损和开关阻抗，从而忽略了线路压降和开关管压降。

相应的电流表示为

(8)

(9)

传输功率计算如下：

(10)

(11)

(12)

逆变电路交流侧状态方程如下：

(13)

下面由上述模型推导逆变器的平均值模型。

由于Ut(t)是周期函数，可以对其进行傅里叶分解：

(14)

式中：

(15)

(16)

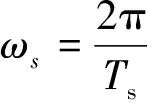
将式(14)代入式(13)可得：

(17)

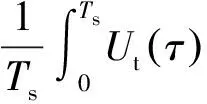
(18)

(19)

这里：

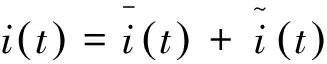
(20)

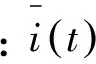
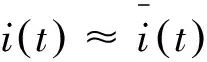
(21)

这里，取平均值定义为

(22)

平均值模型本质上就是忽略开关函数模型的周期分量，保留直流分量。开关函数模型里，周期函数主要是开关函数，将其写成平均值形式如下：

(23)

(24)

式中：d为SPWM占空比，为表述简便，令：

m=2d-1

(25)

将开关函数模型中相应变量以平均值模型表达如下：

(26)

(27)

(28)

(29)

(30)

根据单相逆变电路的平均值模型，建立等效电路见图6。

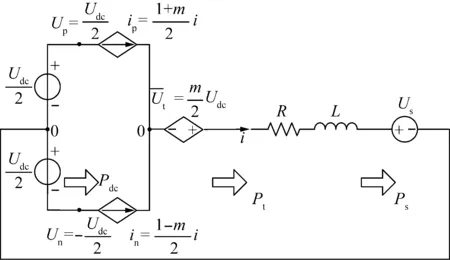
图6 单相半桥逆变器平均值模型等效电路

上述等效电路是对逆变器详细模型即开关电路的简化，在数学模型上它忽略了相应变量的周期分量，在电路表现形式上用受控电压源和电流源取代了高频脉冲控制的开关管。这样，平均值模型既可以表现逆变器的动态特性，又不包括高频分量即开关谐波，达到了本文预期的简化目的。三相逆变电路可以由上述单相逆变电路组合而成，本文不再赘述。

2 分布式电源简化模型仿真验证

前文详细介绍了逆变器接口型分布式电源原动机简化模型和逆变器简化模型，二者组合便是分布式电源整体的简化模型。为了验证前文建立的分布式电源简化模型的可行性和优越性，这里建立光伏并网系统的实际仿真背景[11-13]，将分布式电源的详细模型与简化模型的仿真结果进行对比，仿真示意图如7所示。

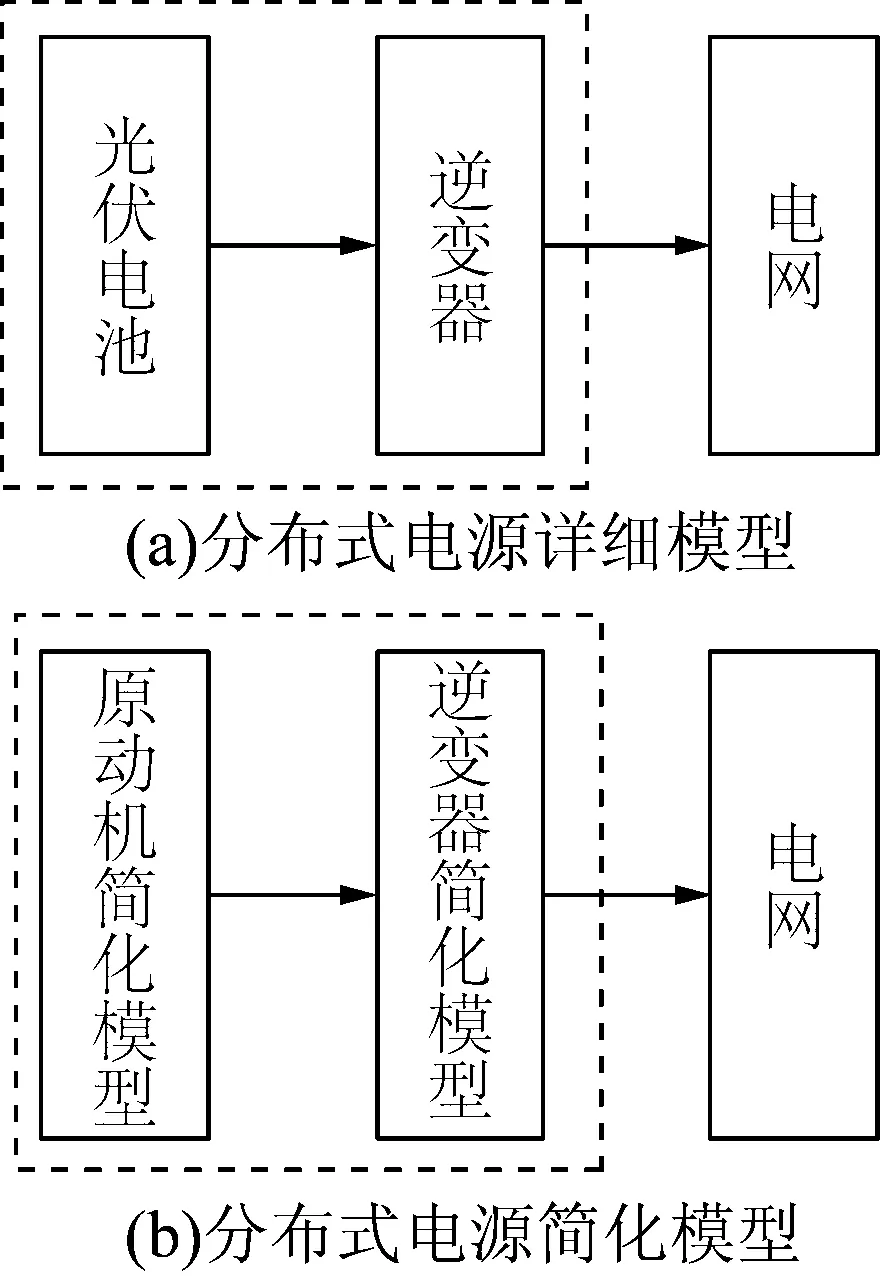
图7 光伏并网仿真模型示意图

这里，光伏电池额定功率设定为100 kW，接有具有MPPT控制算法的DC/DC功率变换器[14]，随时追踪最大功率点以保证最大功率输出。相应地分布式电源简化模型设置与详细模型相同的输出参数。

仿真过程中设计光照强度在仿真过程中产生突变，在0.1 s时光照强度由1 000 W/m2下降到600 W/m2,光伏电池输出功率改变，这样可以将详细模型与简化模型的暂态和稳态性能进行对比。

2种模型仿真结果对比如图8～12所示。从仿真结果对比图可以看出，分布式电源简化模型在稳态时得到了与详细模型相同的仿真结果。 由图8、9、10可以看出，光伏电池在光照发生突变时，由于MPPT算法需要重新追踪最大功率工作点，暂态时间较长，并且影响到后面逆变器的输出功率和直流侧电压的稳定；而原动机简化模型在环境条件改变时可以快速稳定在新的工作状态，略去了详细模型具体的最大功

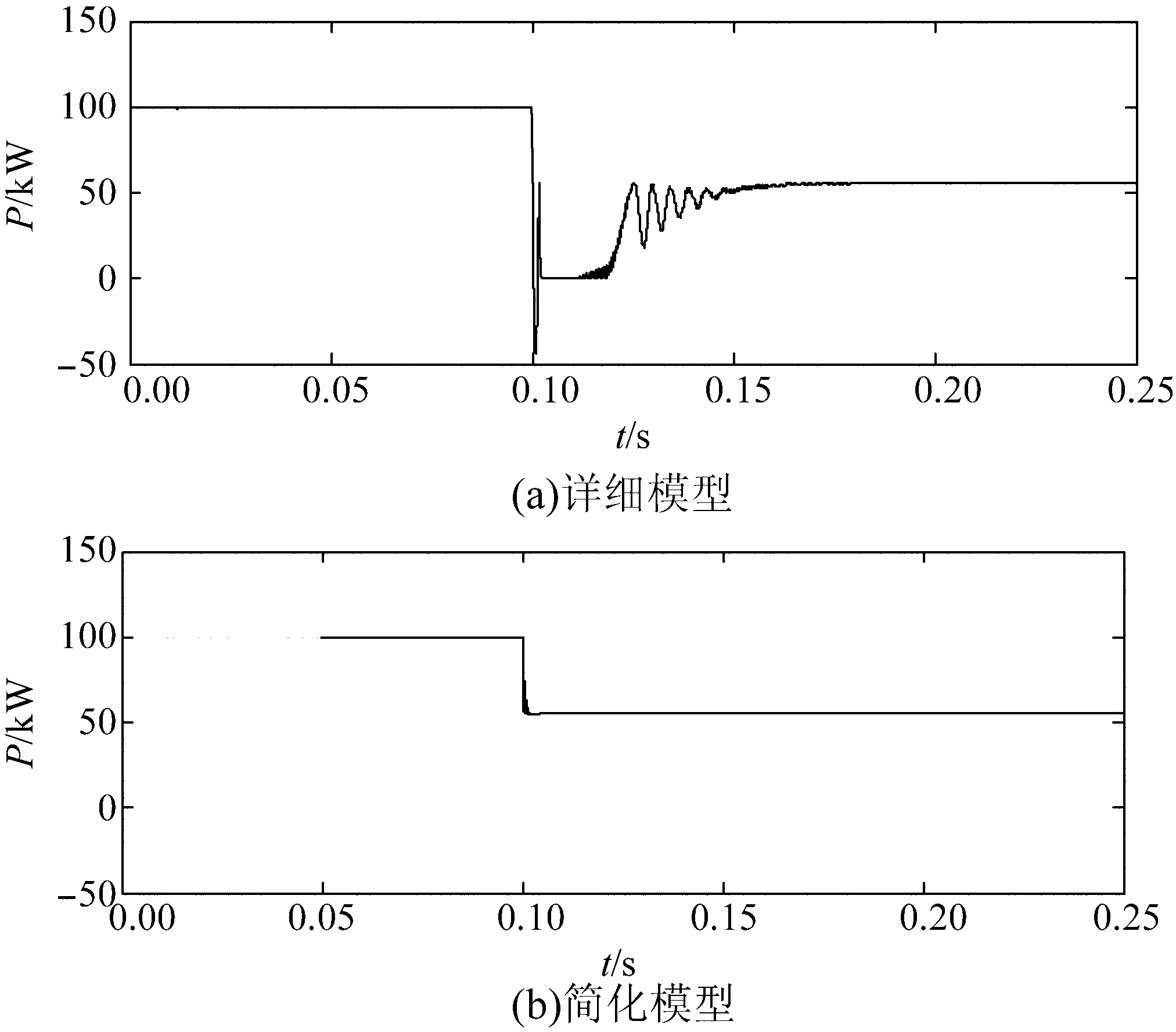
图8 光伏电池输出功率曲线

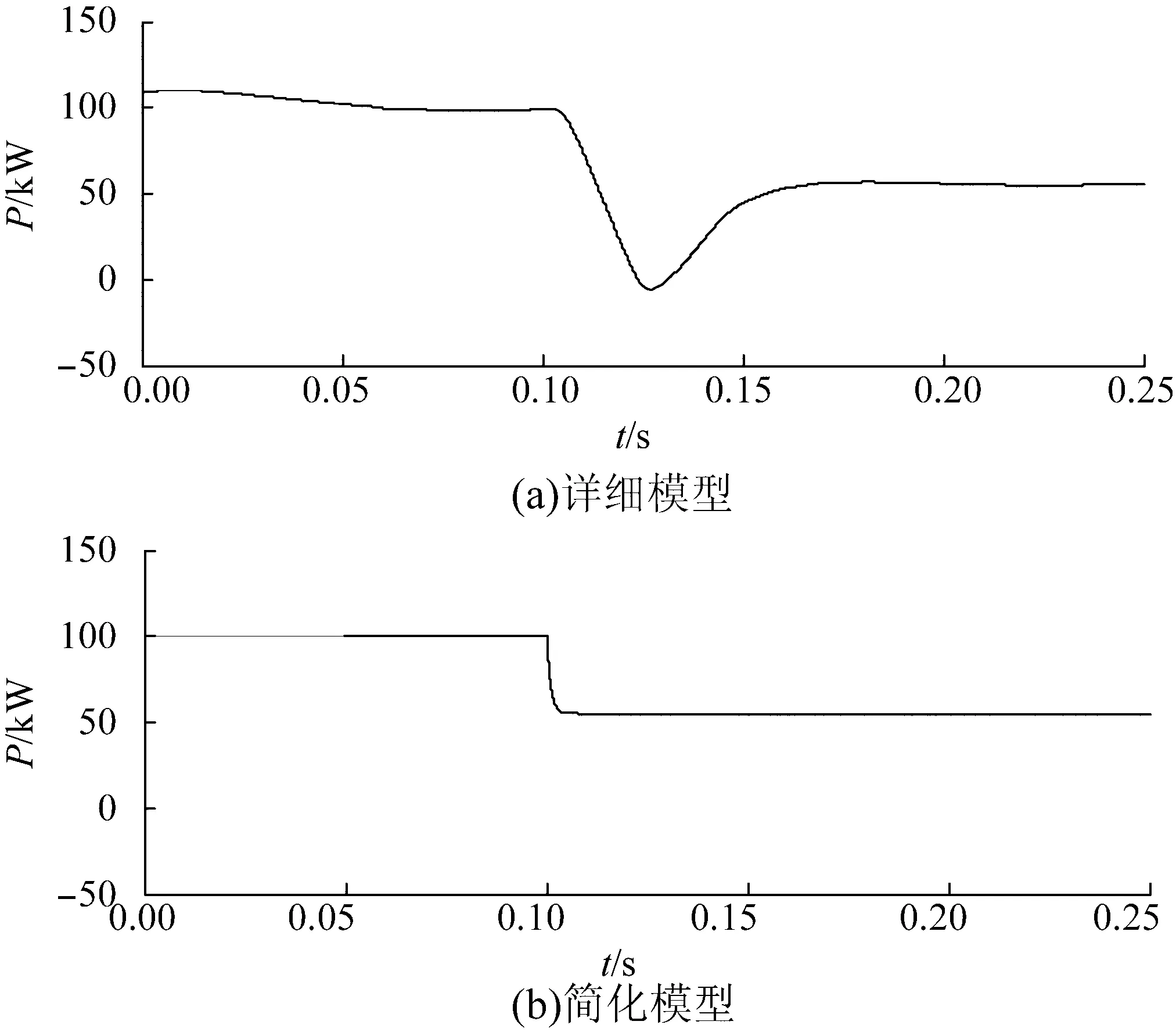
图9 逆变器输出功率曲线

图10 直流侧电压曲线

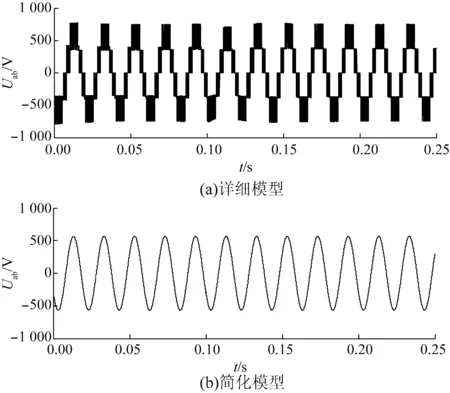
图11 逆变器输出侧线电压曲线

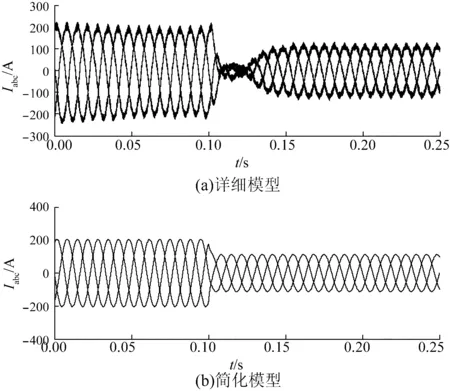
图12 逆变器输出侧三相电流曲线

率追踪时间。由图11、12可以看出，逆变器详细模型输出侧电流电压波形包含了大量的开关谐波，导致波形严重失真，不利于对仿真结果的观察；而逆变器简化模型由于采用平均值模型，滤除了开关谐波，使得输出电压电流波形比较接近理想的正弦波。从仿真结果的对比可以看出，分布式电源的简化模型达到了预期的效果，相较于详细模型优势明显，在某些不需要考虑具体模型暂态反应的仿真环境中，可以达到使用要求。

3 结 论

本文基于逆变器接口型分布式电源的构成，在对详细模型分析的基础上，分别建立了原动机和逆变器的简化模型，设定了光伏并网的具体仿真环境，将分布式电源的详细模型和简化模型作了仿真对比。对比结果表明，简化模型具有可行性和优越性。

[1] 杨新法，苏剑，吕志鹏，等. 微电网技术综述[J]. 中国电机工程学报，2014，34(1)：57-70.

[2] 黄伟，孙昶辉，吴子平，等．含分布式发电系统的微网技术研究综述[J]．电网技术，2009，33(9)：14-18.

[3] 郭力, 王成山. 含多种分布式电源的微网动态仿真[J]. 电力系统自动化, 2009，1(33)：82-86.

[4] 王成山，高菲，李鹏，等. 低压微网控制策略研究[J]. 中国电机工程学报，2012，32(25)：2-8.

[5] 鞠平，蔡昌春，曹相芹. 基于物理背景的微网总体模型[J]. 电力自动化设备，2010，30(3)：7-11.

[6] 马亚辉，李欣然，徐振华. 微网稳定性仿真系统开发中的若干问题研究[J]. 电工技术学报，2013，29(9)：145-154.

[7] 韩奕，张东霞. 含逆变型分布式电源的微网故障特征分析[J]. 电网技术，2011，35(10)：147-152.

[8] Wang D，Peng F Z. Smart Gateway: A DG-based residential electric power supply system[J]. IEEE Transactions on Smart Grid，2012，3(4)：2232-2239.

[9] 王建辉，顾树生. 自动控制原理[M]. 北京: 冶金工业出版社，2005.

[10] Amirnaser Y，Reza I. Voltage-sourced converters in power system[M]. John Wiley & Sons，Inc.，IEEE Press，2012.

[11] 韩学栋，王海华，李剑锋. 小型分布式光伏发电系统设计[J]. 电力建设，2014,35(1)：104-108.

[12] 周念成，闫立伟，王强钢. 光伏发电在微电网中接入及动态特性研究[J]. 电力系统保护与控制，2010，38(14)：119-127.

[13] 于群，曹娜. MATLAB/Simulink电力系统建模与仿真[M]. 北京:机械工业出版社，2011.

[14] 赵庆平，姜恩华，朱 旋. 基于MATLAB的光伏电池最大功率点跟踪研究[J]. 吉林师范大学学报：自然科学版，2013(2)：26-29.

(编辑：张媛媛)

SimplifiedModelforDistributedPowerinMicrogrid

MA Chuan,LIU Yingshu

(Electrical and Automation Engineering Institute of Tianjin University, Tianjin 300072, China)

As microgrid becomes the current research hotpot in the filed of electricity, the specific device’s transient process is not be considered in some simulation studies. In accordance with a detailed model’s essential characteristics of a distributed power, this paper simplifies its components, namely prime mover and inverter, separately and proposes the corresponded simplified models, in order to shorten modeling time and simulation time and eliminate harmonic interference in simulation results. In the simulation background of photovoltaic grid-connected, through the establishment of an overall model of photovoltaic grid-connected, this paper makes a comparison between the detailed model and the simplified model, confirming that the simplified model not only gets the same results in the steady state with the detailed model, but also represents a better transient performance than the detailed model, which achieves the desired requirements for the simplified model.

microgrid; distributed power; simplified model; photovoltaic grid-connected

TM 743

： A

： 1000-7229(2014)06-0044-06

10.3969/j.issn.1000-7229.2014.06.009

2014-04-29

：2014-05-08

马川(1989)，男，硕士研究生，主要从事微网、智能电网方面的研究工作，E-mail：machuan01@126.com；

刘迎澍(1971)，男，博士，副教授，主要从事智能电网、基于Web的信息与控制技术、嵌入式系统及应用等方面的研究工作。