基于改进粒子群算法的微网动态经济调度算法

宁阳天，李相俊，麻秀范，闫鹤鸣，惠东

(1.华北电力大学电气与电子工程学院，北京市 102206；2.中国电力科学研究院电工与新材料研究所，北京市 100192)

基于改进粒子群算法的微网动态经济调度算法

宁阳天1，李相俊2，麻秀范1，闫鹤鸣1，惠东2

(1.华北电力大学电气与电子工程学院，北京市 102206；2.中国电力科学研究院电工与新材料研究所，北京市 100192)

对微网并网运行模式下的动态经济调度进行了研究，建立了优化微网内分布式电源出力的数学模型，同时考虑对主网向微网输入功率的优化。数学模型以最小化微网内总用电成本为目标，目标中将从主网中的购电成本视为用电成本的一部分，在考虑微网内功率平衡以及分布式电源出力大小和爬坡限制的约束条件下，对目标函数进行优化。解决平衡约束时，采用潮流计算的方法，将公共连接点视为潮流计算中的平衡节点，可根据网内出力和负荷平衡情况适时进行调节。求解数学模型时，采用粒子群算法，并对粒子群算法进行改进，在其中加入自适应措施，以解决非凸、高维、非线性的优化问题。典型算例验证表明，所提出的微网动态经济调度模型合理，求解算法具有很好的实用价值。

微网；并网运行；动态经济调度；粒子群算法；自适应

0 引 言

电力系统经济调度(economic dispatch，ED)是电力系统运行与控制的重要研究内容，其本质是研究在满足系统能量平衡和运行极限约束前提下，以经济性最优为目标的约束最优化问题[1]。ED主要用于在考虑包括负荷平衡在内的各种约束条件下，发电成本的最小化，即以发电成本最小为目标函数。ED只考虑一个时点的发电成本最小化，当考虑机组的前后时段的出力约束时，原有的经济调度研究即发展为动态经济调度(dynamic economic dispatch，DED)，从另一个角度来说经济调度包括了静态经济调度(只考虑一个时点)和动态经济调度。DED的研究有利于减少发电成本，节约能耗，提高电力系统运行的经济性与可靠性。同时随着电力市场的发展，DED也可用到电力市场的机组功率分配中[2-5]。

微网作为电力系统的一部分，也需要进行动态经济调度。微网是分布式电源(distributed generation，DG)系统和负荷组成的微型电力网，微网提供了把分布式电源和大电网有效结合起来的方法。微网中的分布式电源包括微型燃气轮机、燃料电池、光伏电池、风力发电、生物质能发电等，其运行方式分为并网运行和独立运行[6-7]，本文仅考虑并网运行的情况。并网运行时，大电网作为微网的重要支撑，可以保证微网内负荷的可靠供电，在分布式电源无法供给微网内负荷时，由大电网通过公共连接点(point of common coupling，PCC)向微网内负荷供电。

由于存在着众多的约束条件，DED属于非凸、高维度、非线性、不可导的优化问题。DED的研究由来已久，各类相应模型与算法十分丰富，算法主要可分为传统算法和智能算法两大类，随着计算机技术的发展，在解决DED问题时，智能算法越来越受到重视。智能算法中的粒子群算法[8-12]、遗传算法[13-16]、进化算法[17-18]、蚁群算法[19]、模拟退火算法[20]都在DED中得到了广泛的应用。与其他智能算法相比，粒子群算法的概念更容易理解，操作起来也更加简单，在动态经济调度中获得了广泛的应用。但粒子群算法在计算过程中存在一定的盲目性，计算时间较长，也容易陷入局部最优。

本文在计算微网内负荷平衡时采用潮流计算中设置平衡节点的方法，求解目标函数时，基于粒子群算法提出了改进措施，加入自适应算法，以增强求解过程寻优的目的性、加快寻优速度、避免陷入局部最优。

1 DED数学模型

1.1 目标函数

电力系统动态经济调度目标是在满足各个约束条件之下，合理分配各机组各时段的出力，在调度期间内系统内的发电成本最小[1]。故目标函数为

(1)

微网中，不同的分布式电源其成本函数的形式不同，如柴油机组为二次成本函数，如下式[14]：

(2)

式中：ai、bi和ci为燃料成本系数。

燃料电池、微型燃气轮机成本函数如下：

(3)

式中：Cfi为燃料成本系数；Cri为运营维护成本系数[14]。

1.2 约束条件

(1)功率平衡约束：

(4)

式中：PPCC,t为PCC点在t时刻的输入功率；Pj,t为网内第j个节点在t时刻的有功负荷，j=1,2,…,m；Ploss,t为t时刻的网损，即微网内要保证分布式电源出力与PCC输入功率之和始终等于各节点负荷与网损之和。

(2)机组出力大小约束。任何机组的运行都必须在其出力上下限范围之内，因此必须满足：

Pmin i≤Pi,t≤Pmax i

(5)

式中：Pmax i、Pmin i分别为第台发电机出力的上限与下限约束。

(3)机组爬坡约束：

(6)

2 改进粒子群算法

粒子群算法是一种模拟社会行为的随机全局优化算法，最早由Keunedy和Ebethart于1995年提出[8]。为适应不同问题的需要，粒子群算法往往加以改进。文献[9]引入优化顺序法，克服粒子寻优的盲目性，从而提高了运算速度。文献[10]采用粒子群算法与非线性原—对偶内点算法结合，得到粒子群—内点混合优化策略，与二者单独运行时相比，在运算速度和精度上都有优势。文献[11]针对平衡约束条件、机组组合状态和冗余机组问题分别提出了循环处理策略、优先启停策略和机会停机策略。

2.1 粒子群算法基本数学模型

在粒子群算法中，所求解问题的可能解用粒子表示，粒子群中每个粒子都是问题的可能解，而粒子则代表了搜索空间的位置，同时每个粒子又可根据目标函数确定一个适应值，通过比较适应值的大小，不断优化粒子的位置。优化过程中，还有一个十分重要的因素就是粒子的速度，在每次迭代中通过速度不断改变粒子的位置，以期获得更好的粒子位置，即更优的解。迭代的基本公式如下：

(7)

pk+1,h=pk,h+vk+1,h

(8)

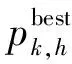
在第1次进行迭代时需要生成粒子群初始位置和初始速度，对于粒子位置中的每个元素都表示某机组、某时刻的出力，对于第i行第t列的元素Pi,t根据下式形成初始值：

(9)

(10)

式中r为0到1的随机数。

最基本的粒子算法中，约束因子K和惯性因子ω的值均为1。在实践中，往往采用自适应的方法对ω进行调整，即

(11)

式中：通常ωmax取0.9；ωmin取0.4；k为迭代次数；kmax为迭代最大次数。

通常

(12)

式中φ=c1+c2，φ>4。

2.2 粒子群算法的改进

由于动态经济调度问题属于高维度、强约束问题，在对粒子位置进行初始化和调整时都容易出现越限问题。因此每次迭代时都根据约束条件对粒子位置进行调整，调整步骤如下：

(1)根据上下限约束对机组出力进行调整，机组越上限时，则将其出力限定在上限，机组越下限时，则将其出力限定在下限。

(2)根据爬坡约束对机组出力进行调整，机组向上爬坡时，若越限，则将机组出力限定在向上爬坡的上限；机组向下爬坡时，若越限，则将机组出力限定在向下爬坡的下限。

(3)根据调整后的机组出力，重新进行潮流计算，确定PCC点的出力状况。

粒子群算法中，随着迭代次数的增加，可能会陷入局部最优，此时粒子的速度也会随之减小，故需要对粒子速度进行调整，即

v1=v0+Δv

(13)

式中，v0、v1分别为调整前后的粒子速度，Δv为调整的速度量，调整时采用自适应算法，自适应算法公式如下：

(14)

式中：vini为粒子群算法中所设置的初始速度；r3为-0.1到0.1的随机数；r4为-0.01到0.01的随机数，对于随机数r3、r4可以根据实际需用设定，而λ则根据下式计算：

(15)

3 算例分析

3.1 算法流程

(1)输入机组、微网负荷等相关参数与数据。

(2)生成粒子的初始位置与速度。

(3)计算每个粒子的适应值，以此确定局部最优值和全局最优值。

(4)根据式(7)、(8)对粒子位置进行迭代。

(5)采用改进的粒子群算法调整粒子位置。

(6)根据式(13)～(15)对粒子速度进行调整。

(7)判断是否达到最大迭代次数且前后再次迭代结果变化率小于所设定的精度，若不满足判断条件，转到(3)继续迭代，若满足判断条件，输出最终的粒子位置，即最后优化的结果。

3.2 算例数据

本文算例采用文献[19]中17节点的微网系统，其结构参数与负荷数据如表1所示，表中最后一列为某一典型日的负荷，表示末节点的最大负荷，其各个节点负荷的功率因数均为0.85。工业负荷、商业负荷、居民负荷的日负荷比例曲线图(与该日最大负荷的百分比)如图1所示。微网内分布式电源参数采用文献[7,12]的分布式电源的相关参数，并进行了一定的修正，如表2所示，微网中连接有分布式电源的节点为5、6、7、8、9、12，机组1、2为柴油机组，机组3、4为燃料电池，机组5、6为微型燃气轮机。微网从主网的购入电量电费为0.5元/(kW·h)。

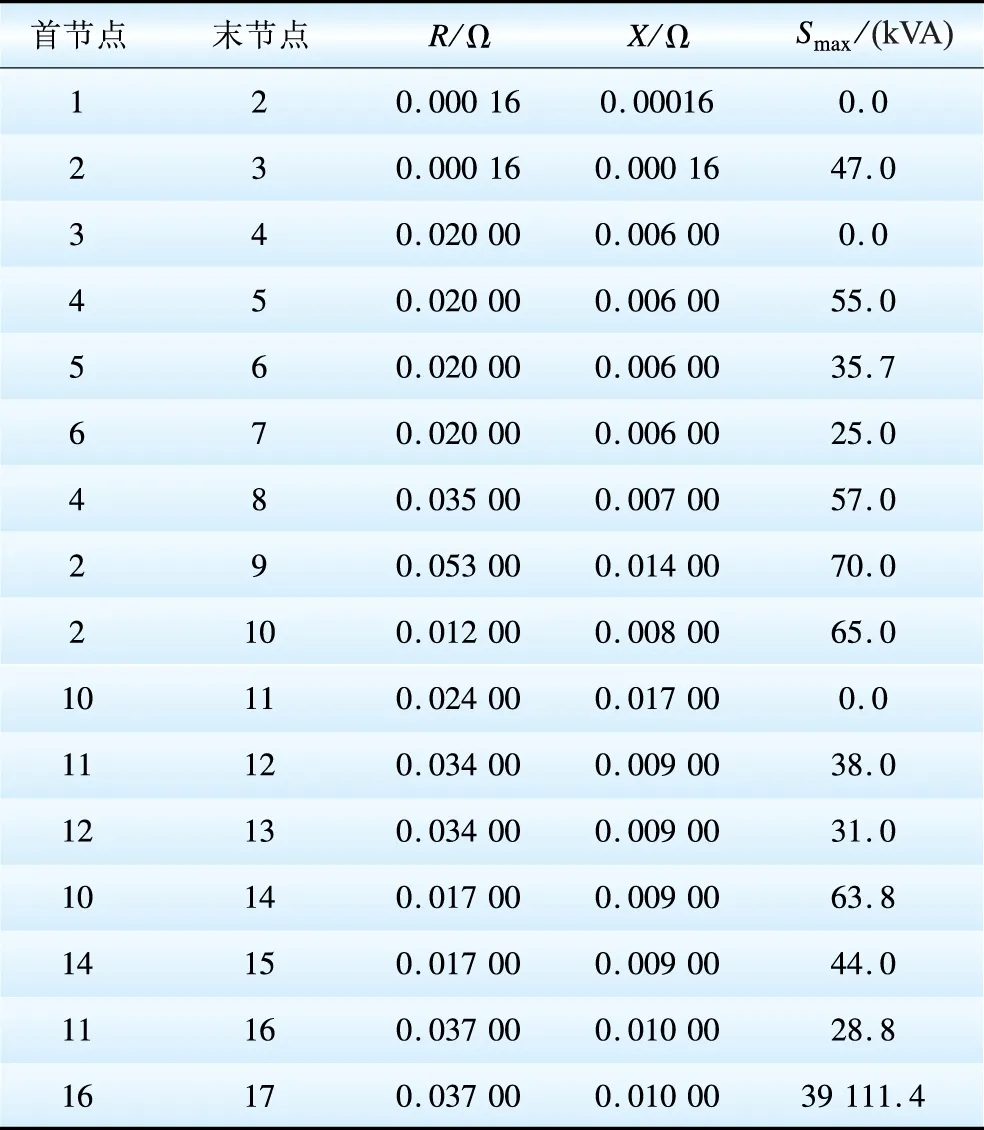
表1 微网参数

图1 三类日负荷曲线

3.3 算例结果

在本文的计算中，粒子群算法参数如下：惯性因子ωmax=0.9，ωmin=0.4，学习因子c1=c2=2.05迭代次数上限为2 000次。

表3为分布式电源24 h优化出力结果以及PCC点向微网供给的功率。计算得到总费用为9 845.5元。

图2给出了考虑自适应算法(实线所示)和未考虑自适应算法(虚线所示)的优化过程，图中横轴表示迭代次数，纵轴表示每次迭代的全局最优值。从图2可以看出，加入提高粒子速度的自适应法则后，求解速度优势明显，在迭代到第500次附近时收敛效果出现明显的区别，最优值下降的速度更快，有效地解决了求解过程中陷入局部最优的问题。最后两者在1000次附近都实现了收敛，但加入自适应算法的收敛结果更好，而未加入自适应算法的最后优化结果为9 923.6元，发电成本要比加入自适应算法的结果多78.1元，高出0.79%。说明改进后的粒子群算法，能够较好地解决微网并网时的动态经济调度问题，提高了求解速度，并可得到更好的优化结果。

表2 分布式电源参数

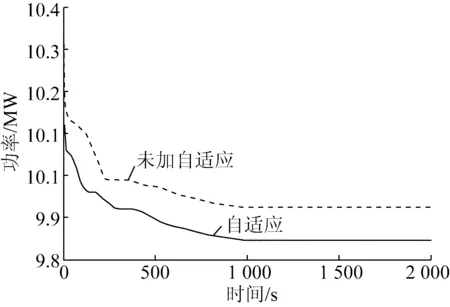
图2 算法迭代过程对比

4 结 论

本文在考虑分布式电源出力、爬坡限制的前提下，通过与大电网的配合，满足了微网内负荷的需求，采用考虑自适应的改进粒子群算法对目标函数进行求解，对典型的微网模型进行了求解。得到以下结论：

(1)该方法优化了分布式电源1天的出力计划，得到了各时点PCC向微网负荷提供的功率。

表3机组及PCC点出力数据

Tab.3OutputdataofunitandPCCkW

(2)通过根据约束条件对粒子位置进行调整和加入粒子速度调整的自适应法则对粒子群算法进行改进，避免了粒子群算法陷入局部最优，可有效地解决该非凸、高维度、非线性、不可导的优化问题，提高求解速度。

(3)基于微网17节点算例验证了本文提出的改进粒子群算法，有效地提高了运算的速度并得到了更好的优化结果。

[1]周玮，孙辉，顾宏，等.含风电场的电力系统经济调度研究综述[J].电力系统保护与控制，2011，39(24)：148-154.

[2]Li X，Yamashiro S，Wu L，et al.Generation scheduling in deregulated power market taking into account transmission loss allocation[J].IET Generation，Transmission & Distribution，2010，4(7)：883-892.

[3]Li X，Yamashiro S，Wu L，et al.Optimization of DC power flow by

transmission loss allocation method[C]//Power and Energy Engineering Conference.Wuhan China：IEEE，2009：1-6.

[4]Li X，Yamashiro S.Generation scheduling and economic estimation of power systems including bilateral contracts[J].Electrical Engineering in Japan，2007，158(2)：20-30.

[5]Li X，Yamashiro S.Unit commitment taking into account reactive power[J].Electrical Engineering in Japan，2008，162(3)：17-26.

[6]Li X，Song Y J，Han S B.Frequency control in micro-grid power system combined with electrolyzer system and fuzzy PI controller[J].Journal of Power Sources，2008，180(1)：468-475.

[7]李振动.微网的经济调度研究[D].北京：华北电力大学，2012.

[8]吴杰康，韩军锋，刘蔚，等.基于反捕食粒子群算法的电力系统经济调度方法[J].电网技术，2010，34(6)：59-63.

[9]张燕.含风电场的电力系统动态经济调度[D].北京：华北电力大学，2011.

[10]周玮.含风电场的电力系统动态经济调度问题研究[D].大连：大连理工大学，2010.

[11]王召旭.含风电场的电力系统动态经济调度的研究[D].北京：华北电力大学，2011.

[12]苗雨阳，卢锦玲，朱国栋.基于改进多目标粒子群算法的微电网并网优化调度[J].电力科学与工程，2012，28(7)：15-20.

[13]邢维建.遗传算法在电力系统经济调度中的应用研究[D].保定：华北电力大学，2005.

[14]刘小平，丁明，张颖媛，等.微网系统的动态经济调度[J].中国电机工程学报，2011，31(31)：77-84.

[15]Yalcinoz T，Altun H，Uzam M.Economic dispatch solution using a genetic algorithm based on arithmetic crossover[C]//Power tech proceedings，2001 IEEE Porto：IEEE，2001，2：4 pp.vol.2.

[16]孙元章，吴俊，李国杰，等.基于风速预测和随机规划的含风电场电力系统动态经济调度[J].中国电机工程学报，2009，29(4)：41-47.

[17]夏澎.基于差分进化算法的含风电场电力系统动态经济调度[D].北京：华北电力大学，2010.

[18]夏澍，周明，李庚银.含大规模风电场的电力系统动态经济调度[J].电力系统保护与控制，2011，39(13)：71-77.

[19]艾欣，崔明勇，雷之力.基于混沌蚁群算法的微网环保经济调度[J].华北电力大学学报，2009，36(5)：1-6.

[20]Chen C L.Simulated annealing-based optimal wind-thermal coordination scheduling[J].The Institution of Engineering and Technology，2007，1(3)：447-455.

(编辑：蒋毅恒)

MicrogridDynamicEconomicDispatchBasedonImprovedParticleSwarmOptimization

NING Yangtian1, LI Xiangjun2, MA Xiufan1, YAN Heming1, HUI Dong2

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China;2.Electrical Engineering and New Material Department, China Electric Power Research Institute, Beijing 100192, China)

This paper studied the dynamic economic dispatch of microgrid operation with grid mode, and established a microgrid optimization mathematical model of distributed generation output, simultaneously taking into account the power input from main grid optimization. The mathematical model objective was to minimize the total electric cost in microgrid, in which the purchase cost from the main grid was treated as part of the electric cost. With considering the power balance within the microgrid, the distributed generation output and the ramp constraint conditions, the objective function was optimized. The power flow calculation was used to solve power balance constraint, in which the point of common coupling was treated as the slack bus, and the adjustments could be done timely according to the balance situation between output and load in microgrid. This paper used particle swarm optimization (PSO)to solve the mathematical model, and improved PSO with adding self-adaptation measure to solve non-convex, high-dimensional, nonlinear optimization problems. Typical numerical example shows that the proposed model for microgrid dynamic economic dispatch is reasonable and the algorithm has good practical value.

microgird; operation with grid; dynamic economic dispatch; particle swarm optimization; self-adaptation

国家自然科学基金项目(51107126)；国家电网公司科技项目(DG71-12-002)。

TM 73

： A

： 1000-7229(2014)06-0026-05

10.3969/j.issn.1000-7229.2014.06.006

2014-02-24

：2014-03-06

宁阳天(1990)，男，硕士研究生，研究方向为电力经济、电力系统运行与控制，E-mail：nsunsky1990@126.com；

李相俊(1979)，男，博士，高级工程师，研究方向为电池储能系统控制、新能源与分布式发电、电力系统运行与控制；

麻秀范(1970)，女，博士，副教授，主要研究方向为电力经济，电力系统规划与运行；

闫鹤鸣(1986)，女，硕士，研究方向为电力经济；

惠东(1968)，男，博士，教授级高级工程师，主要研究方向为大规模储能系统、新能源与分布式发电技术。