一个不等式的证明方法探讨

景慧丽， 杨宝珍， 刘 华， 屈 娜

(第二炮兵工程大学 理学院，西安 710025)

不等式的证明是高等数学课程的重要组成部分，由于不等式的证明没有固定模式，证明方法因题而异，灵活多变[1，2]，所以，不等式的证明也是学员感到最困惑的问题之一.就某校期末考试题中的一道不等式的证明进行探讨，提出3种证明方法，进而培养学员的发散思维.

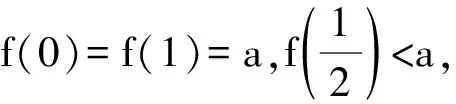
证法1 利用泰勒(Taylor)公式证明

从而有

(1)

(2)

式(1)(2)相加得

所以

因此

f″(ξ1)+f″(ξ2)>0

取f ″(ξ)=max{f ″(ξ1)，f ″(ξ2)}，显然ξ∈(0，1)，且满足f ″(ξ)>0.

注1 一般地，含有二阶及二阶以上的导数的不等式，常用带有拉格朗日型余项的泰勒公式来证明.

注2 要利用泰勒公式来证明不等式，就要对函数f(x)在一点x0处进行泰勒展开，这就需要恰当地选择x0.选择x0没有一般规律可循，但通常选用区间的端点、中间点、函数的极值点、导数为零的点或信息给的比较多的点(如函数在该的值或一阶导数的值已给出等)等特殊点作为x0[1].

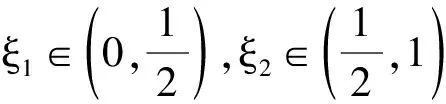
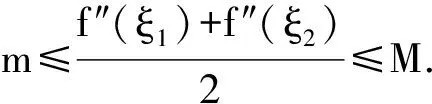
上述证明方法不正确的原因是：题目中只说f(x)在[0，1]上二阶可导，即只说明f ″(x)存在，没说明f ″(x)在[0，1]上连续，所以不能用闭区间上连续函数的最值定理和介值定理.只有当函数满足在闭区间上连续时才存在最值定理和介值定理.若题目中只给出闭区间，没说明函数连续；或只给出函数连续，而不是闭区间，则函数未必存在最值.所以应用定理时一定要满足定理成立的条件，而不能随心所欲.

证法2 利用拉格朗日(Lagrange)中值定理证明.

因为函数f(x)在区间[0，1]上二阶可导，所以f ′(x)在[ξ1，ξ2]⊂[0，1]上也满足拉格朗日中值定理的条件，由拉格朗日中值定理知至少存在一点ξ∈(ξ1，ξ2)⊂(0，1)，使得

注4 方法2是对函数f(x)及f ′(x)分别利用拉格朗日中值定理证明的，实际上，拉格朗日中值定理是泰勒中值定理的特殊情形，泰勒中值定理是拉格朗日中值定理的推广.因此，可以说方法2本质上用的也是泰勒公式.

证法3 利用反证法证明.

假设不存在ξ∈(0，1)，使f ″(ξ)>0，那么对任意的x∈(0，1)，都有f ″(x)≤0.下面分3种情况讨论：

情况1 若f ″(x)≡0，则f ′(x)≡C，其中C为某个常数.

情况2 若f ″(x)<0，则f ′(x)单调递减.

情况3 若对区间(0，1)中的x，既有满足f ″(x)=0的点，也有满足f ″(x)<0的点，则f ′(x)在单区间(0，1)中单调不增.

显然这与情况1，2及3都矛盾，故假设不成立，因此原结论成立.

注5 尽管方法3用的反证法，但其关键和核心是用拉格朗日中值定理来否定假设的.

注6 反证法其独特的证题方法和思维方式对培养学员逻辑思维能力(特别是逆向思维能力)和创造性思维能力有着重大的意义，是锻炼学员思维的多样性、敏捷性、灵活性的极好素材.

由上述证明可以看出，对一道题目的解法往往有不同的思路，知识点之间表面上看是相互独立的，实际上它们具有一定的联系. 其实，高等数学课程中许多知识体系都是相关联的，在高等数学课程教学中，教员应坚持经常性地向学员灌输知识体系中的相互关系，使学员体会知识的产生和过程的发展，深刻理解和掌握数学的基本思想和方法，从而提高学员的学习兴趣，加深对知识的理解.

总之，高等数学课程中很多题目都可以用多种思路和方法来求，教员在应用这类一题多解的题目组织教学时，必须以学员为本，鼓励学员积极参与教学活动，敢于标新立异，勇于提出问题，开展交流和讨论，这样才有利于学员突破思维的局限性，培养学员的发散思维和综合能力.

参考文献：

[1] 吴忠祥.工科数学分析基础教学辅导书(上)[M].北京：高等教育出版社，2006

[2] 曾静.不等式证明的三种方法[J].重庆工商大学：自然科学版，2013，30(7)：16-18