基于定子电流的MRAS转速估计方案

张笠君， 阮 毅， 吴晓新， 柳 巍

(上海大学 机电工程与自动化学院，上海 200072)

0 引 言

无速度传感器矢量控制需要准确估算转速和磁链信息。目前，应用较广的有模型参考自适应系统(Model Reference Adaptive System，MRAS)、Kalman滤波、人工神经网络等[1-2]。基于MRAS的转速估算发展到现在可以分成：(1)基于转子磁链误差的MRAS转速估算方案，也是目前最常用的一种MRAS转速估算方案，称为传统MRAS转速估算[2-3]；(2)基于反电动势的MRAS转速估算方案，将计算的反电动势和测量的反电动势的误差进行比较，得到转速误差[4]；(3)基于定子电流误差的MARS转速估算方案。通过定子电流模型计算出定子电流，与测量的定子电流进行比较，得到转速误差信号[5]。

文献[2-3]将电压模型作为参考模型，电流模型作为可调模型，为传统的MRAS转速估算方案。该方案结构并不复杂 、计算较简单，但是电压模型中存在纯积分环节，会产生积分误差和饱和，影响转子磁链输出。文献[3]提出了一种改进方法，用高通滤波器替换纯积分环节，再补偿一个转子磁链误差，可以抑制积分漂移。文献[4]是基于反电动势的MRAS转速估算方案。该方案提高了系统的鲁棒性，但是同样使用电压模型作为参考模型，在计算转子磁链时，由于定子电阻压降作用明显，测量误差淹没了反电动势，使得观测精度较低。

本文在基于传统MRAS的基础上，将参考模型改为感应电机本身，即通过感应电机的定子电流构造转速辨识模型。这种方法对电机参数依赖比较小、动态响应快，不含纯积分环节。通过MATLAB/Simulink对传统MRAS转速估算方案和本方案进行仿真。比较结果表明，本文介绍的这种方法具有较高的转速辨识精度和动态响应。

1 传统MRAS转速估算方案

传统的模型参考自适应是将电压模型作为参考模型，电流模型作为可调模型，在电流模型中有转速信号，通过自适应律使可调模型与参考模型的输出宏偏差尽可能小，使计算的转速尽可能接近于实际的转速[5-6]。传统的MRAS原理如图1所示。

图1 传统MRAS原理图

电压模型方程为[2]

(1)

电流模型方程为[2]

(2)

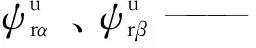
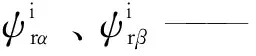
Lr——转子电感；

Lm——互感；

Ls——定子电感；

usα、usβ——两相定子电压；

isα、isβ——两相定子电流；

Rs——定子电阻；

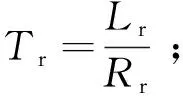
ωr——转子角频率。

根据Popov 超稳定理论，按MRAS 参数的结构，速度估算子模块将估算转速取为比例积分形式。自适应律为

(3)

2 基于定子电流的转速估算方案

由式(1)可知，电压模型并不是一个最理想的参考模型，尤其是在低速的时候，定子电阻压降不可忽略，造成转速估算不准确。

因此提出了基于定子电流的MRAS转速估算方案。该方案是将电机本身作为参考模型，通过测量的电机实际电流与通过定子电流模型计算得出的电流偏差εis，经过自适应律调节，使偏差εis尽可能小，即计算出的电流与测得的电流尽可能接近，转速就尽可能接近于实际转速。没有纯积分环节，转子磁链计算不需要定子电阻参数，因此在中低速时辨识精度也较高。

根据异步电机在α、β坐标系中的状态方程得定子电流计算式[7]：

(4)

估算电流为

(5)

将实际定子电流减去估算电流得电流误差为

(6)

(7)

由式(7)得

(8)

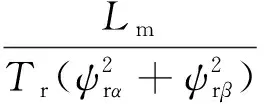
(9)

由式(2)、式(6)、式(9)得到基于定子电流的MRAS转速估算原理图如图2所示。

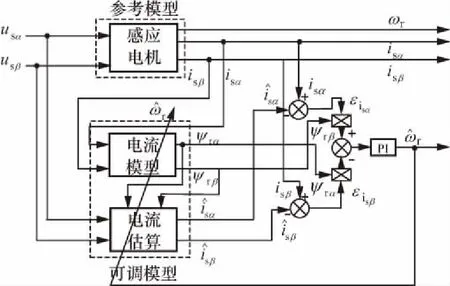
图2 基于定子电流的MRAS转速估计原理图

3 基于定子电流的MRAS转速估算矢量控制模型

速度反馈信号由MRAS速度辨识模块输出，采用电气系统模块库和Simulink模块可以建立仿真模型，其系统框图如图3所示。

图3 基于定子电流的MRAS转速估算矢量控制系统框图

4 与传统方案仿真结果比较及分析

为验证上述速度估算法的正确性及可行性，在MATLAB /Simulink 下建立了无传感器矢量控制仿真系统，并进行仿真。同时与传统的MRAS转速估算方案进行比较。仿真采用的异步电机额定参数：PN=3 kW、fN=50Hz、np=2、UN=380 V、Rs=2.22 Ω、Rr=3.108 Ω、Lm=0.232 4 H、Ls=Lr=0.008 3 H、J=0.142 5 kg·m2。

仿真时空载起动，在系统运行到t=1 s时，突加一个阶跃负载转矩，大小为10 N·m。加载响应仿真结果如图4所示。图4(a)为转速波形，图4(b)为转矩波形，图4(c)为实际转速与估算转速误差波形。

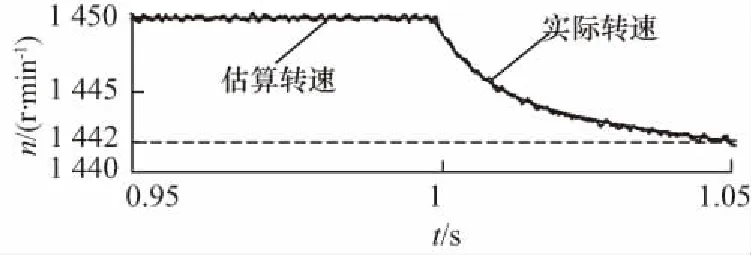
(a) 转速波形

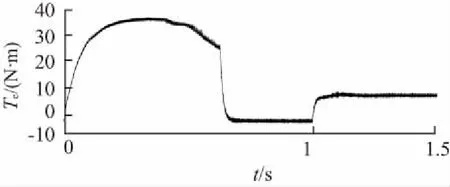
(b) 转矩波形

(c) 实际转速与估算转速误差图4 加载响应仿真结果

由图4可知，给定转速为1 450 r/min，加载之后，实际转速下降至1 442 r/min，偏差εn=0.5%，略微下降，实际转速与估算转速误差为Δn=1.2 r/min。说明系统在加载之后还能够保持稳定。

两种方案的动态响应如图5所示。电机从给定转速1 200 r/min起动，1 s之后给定突加到1 450 r/min的动态响应曲线。

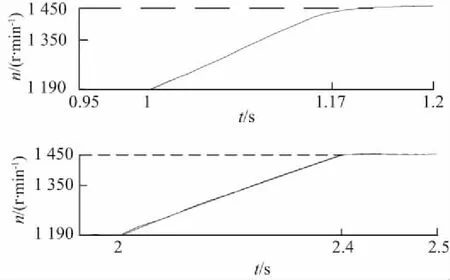
(a) 转速波形

(b) 实际转速与估计转速误差图5 动态响应

图5(a)是基于定子电流的MRAS转速估算仿真图。图5(b)是基于传统的MRAS转速估算仿真图。定子电流MRAS转速从1 200 r/min上升到1 450 r/min，所用时间为0.17 s，稳态误差Δn=0.04 r/min；传统MRAS上升时间为0.4 s，稳态误差Δn=4 r/min。从上述数据可以看出，高速时两种估算方法的误差都不是很大，但本文介绍的方法误差更小，响应更快。

转速200 r/min时，两种方案的仿真结果如图6所示。

从图6可看出，在转速为200 r/min的中低速阶段，定子电流方案的实际转速与估算转速误差Δn=3 r/min，而传统方案的实际转速与估算转速误差Δn=50 r/min，误差很大，并且稳态时转速不稳定。说明本文介绍的基于定子电流方案在中低速阶段估算准确，误差小，稳定性好。

(a)定子电流方案实际转速与估计转速误差

(b)传统方案实际转速与估计转速误差图6 转速为200 r/min时，两种估算方案实际转速与估算转速误差

5 结 语

本文根据定子电流和转子磁链方程在两相坐标系上推导出了异步电动机MRAS转速辨识方法，利用电流偏差和磁链幅值进行转速偏差的计算，系统鲁棒性强，且结构简单。仿真试验结果表明系统速度估计准确、稳定性好、收敛速度快、对给定信号的跟踪能力强，能够满足现代交流调速的高性能要求。

【参考文献】

[1] KOWALSKA T O，DYBKOWSKI M． Stator-current-based MRAS estimator for a wide range speed-sensorless induction-motor drive[J]．IEEE Trans Ind Electron，2010，57( 2) : 1296-1308．

[2] SCHAUDER C. Adaptive speed identification for vector control of induction motors without rotational transducers[J]. IEEE Trans Ind Appl, 1992，28(5):1054-1061.

[3] 陈名辉，阮毅，宗剑,等. 无速度传感器在矿用电机车矢量控制系统中的应用[J]．电机与控制应用，2012,39(2)：17-20.

[4] PENG F Z, FUKAO T. Robust speed identification for speed-sensorless vector control of induction motors[J]. IEEE Trans Ind Appl, 1994,30(5):1234-1240.

[5] 祝龙记，王宾. 基于MRAS矢量控制系统的仿真研究[J]．电工技术学报，2005,20(1)：60-65.

[6] 张毅，阮毅，张毅鸣,等. 基于dsPIC6010 的牵引型变频器控制系统设计[J]． 电机与控制应用，2009( 2) : 3-6．

[7] 刘福才，陈龙，韩会山. 基于定子电流的MRAS矢量控制系统转速辨识[J]．控制工程，2007(7):189-191.