永磁同步伺服电机二自由度控制*

李 明， 程启明， 陈 根， 王鹤霖， 邓 亮

(上海电力学院 自动化工程学院， 上海 200090)

0 引 言

随着我国工业化进程不断加快，伺服驱动系统在越来越多的场合得到了应用。永磁同步电机具有高能量转换效率、高功率密度、刚性结构、快升速和高转速惯性比等优点。随着高性能永磁材料的发展及永磁材料价格的下降，永磁同步电机调速系统也越来越受到了人们的重视[1-2]。

传统的伺服电机控制通常采用常规PID控制。虽然该控制手段在工业上已经趋于成熟，但存在其固有的缺陷。常规PID控制不能独立地对输出的响应特性和负载扰动进行补偿[3-4]。

为了解决常规PID控制器存在的缺陷和问题，改善系统的控制性能，国内外学者进行了广泛的研究，提出了多种控制方法，包括自适应逆推控制、鲁棒控制、滑模变结构控制等非线性控制方法，以及基于人工智能的神经网络、模糊控制、遗传算法等新型智能控制方法。在交流传动伺服系统中，针对永磁同步电动机这一多输入、强耦合的非线性系统，这些控制方法存在计算量过大、模型难建立和控制参数无法选取等问题，导致在工程中很难得到实际应用[5-6]。

二自由度控制的核心思想就是在常规PID控制的基础上，将PID控制器分解为两个独立的变量，分别对给定信号和外界扰动进行控制，从而使系统的跟随特性和抗干扰特性同时达到最优。二自由度控制系统已在工业过程控制领域得到了较为广泛地应用[7-10]。

总之，大数据就像是一场数据革命，它为各行各业做出了巨大贡献。然而它面临的挑战也是十分严峻的，我们只有把握机遇，积极应对这些挑战，才能让大数据为我们所用。大数据运用有助于引领高校教育创新变革，提升教学、科研、管理服务水平和质量，我们应该进一步加大大数据在高校教育的应用研究。

本文将二自由度控制方法引入到伺服传动控制系统中，以解决PID控制方法存在的问题，期望获得更好的调速性能，分析了二自由度控制器的数学模型及其数字化实现，并将二自由度算法引入永磁同步伺服电机的矢量控制系统，最后通过软件仿真与实际工程应用验证所述控制方案的有效性和可行性。

1 常规PID控制器与二自由度控制器

1.1 常规PID控制器

PID控制作为一项经典控制理论，在工业生产中得到了广泛应用。目前，绝大多数工业控制器都采用了PID控制器或其改进型。PID控制器具有结构简单、易实现、鲁棒性强等优点。常规PID控制器结构如图1所示。它由比例P、积分I和微分D组成，其算式为

(1)

式中：e——偏差信号；

Kp——比例；

Ki——积分；

Kd——微分系数。

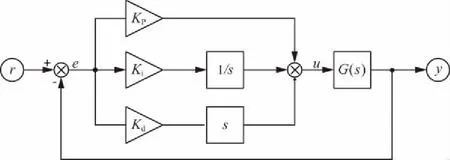
图1 常规PID控制器结构图

在实际工程中，PID控制器通常通过数字化芯片软件编程实现。为了在软件中模拟PID控制器的功能，需要对式(1)进行数字化处理。本文选取增量式PID算法，其基本算式为

(2)

(3)

式中：Ts——采样周期；

Td——微分时间常数。

整理得

(4)

虽然PID控制器有很多优点，但是常规PID控制器只能设置一组控制参数，是一种一自由度控制器。若要获得较好的跟随特性，则干扰抑制能力通常较差；若要获得较好的干扰抑制特性，则跟随特性则相对较差，两者不能同时兼顾。因此，通常情况下PID控制器的参数整定采用折中处理[2]。这种方法虽然能够满足一般控制系统的要求，但对于交流伺服传动系统而言，跟随性能和控制精度是决定控制器好坏的最关键因素，而采用折中处理的PID控制器并不能实现良好的控制性能。此外，反馈控制的控制信号总是滞后于干扰信号，如果干扰不断施加，则不可避免地存在稳态位置跟踪误差，从而影响了系统最终的控制性能。

1.2 二自由度控制器模型

二自由度控制器的结构主要包括前馈型、滤波型、反馈补偿型和回路补偿型。本文选取最常用的前馈型二自由度模型进行说明，其控制系统的结构如图2所示。图中，F1(s)、F2(s)分别表示反馈控制器和前馈控制器；d为干扰信号。二自由度控制系统由输入信号的前馈通道F2(s)和按误差控制的反馈通道F1(s)组成。其中，前馈通道F2(s)主要完成对给定信号的跟踪；反馈通道F1(s)作为主通道则实现对由扰动和模型误差产生的偏差进行补偿。

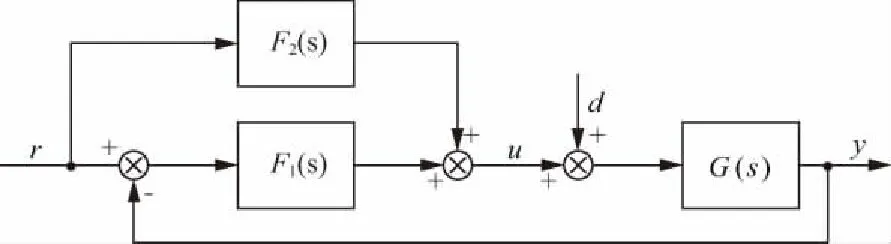
图2 前馈型二自由系统控制结构

图2中，控制器输量为

u=(F1+F2)r-F1y

(5)

令

F2=αΚp+βΚds，Fr=F1+F2,Fy=F1

(6)

式中：α、β为比例系数。

可得前馈型二自由度控制器的数学模型为

(7)

取

b=1+α，c=1+β

(8)

可得

(9)

根据式(9)可得前馈二自由度控制器的结构，如图3所示。

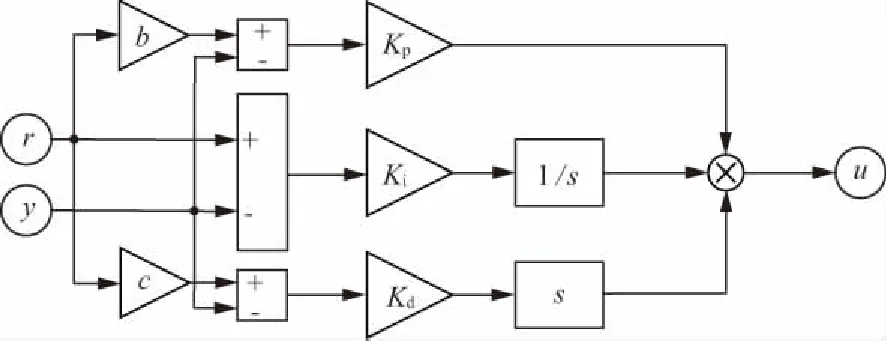
图3 前馈型二自由度控制器结构图

由此推出，输出值y到给定值r、扰动值d到输出值y的传递函数分别为

(10)

(11)

若想得到良好的跟踪特性，则需要同时定Kp、Ki、Kd、b和c的参数；若想获得良好的扰动抑制特性，只需整定Kp、Ki、Kd的参数即可。为了同时获得较好的跟踪特性和干扰抑制特性，可以按干扰抑制特性最优的原则先整定Kp、Ki、Kd的参数，然后再通过调整b、c的值获得较好跟随特性。

将(9)式数字化处理可得到

Δu(k)=bKp[e(k)-e(k-1)]+Kie(k)+

cKd[e(k)+e(k-2)-2e(k-1)]

(12)

整理得

(13)

式(13)即为增量式二自由度PID算法。

1.3 两种控制方法仿真比较

为了测试图4的前馈型二自由度控制器控制性能，本文选取一个理想直流电机模型作为被控对象。其基本参数如下：电枢电阻2 Ω，电枢电感0.5 H，转动惯量0.02 kg·m2；一般PID控制器的参数：Kp=0.2，Ki=1.0，Kd=0.06；前馈型二自由度控制器的参数：Kp=0.2，Ki=1.0，Kd=0.06，b=1.05，c=1.05。可分别得到常规PID、前馈型二自由度两组控制器的n-t响应曲线，如图4所示。

图4 直流电机的n-t响应曲线

由图4可知，采用二自由度控制器，可以在不改变系统干扰抑制特性的前提下，获得比常规PID控制器更好的跟随性能。

2 基于二自由度控制的永磁同步伺服电机矢量控制系统结构

永磁同步电动机本身为一多输入、强耦合的非线性系统，为了使调速系统具备优良的动、静态性能，且能够自动适应外界参数的变化，就需要选择良好的控制策略，以提高系统的快速性、稳定性和鲁棒性。

目前，永磁同步伺服调速系统通常采用矢量控制策略。矢量控制的基本思想是在普通的三相交流电动机上设法模拟直流电动机转矩控制的规律，在磁场定向坐标上，将电流矢量分解成产生磁通的励磁电流分量和产生转矩的转矩电流分量，并使两分量相互垂直，彼此独立，然后分别进行调节，获得像直流电机一样良好的动态特性。

本文选取id=0(id为d轴电流)的矢量控制算法。该控制方法简单易于实现，没有涉及电枢反应的去磁问题，且在表贴式永磁同步电机系统中，id=0的磁场定向控制等于最大转矩电流比控制，具有电流利用率高、转矩控制特性好、实现电机转矩的线性控制便利等特点。基于id=0矢量控制策略的位置伺服控制系统结构如图5所示。

图5 永磁同步伺服电机矢量控制系统结构

图5中，APR、ASR和ACR 分别表示位置控制器、速度控制器和电流控制器。其中，位置环和速度环构成机械外环，电流环为内环。机械外环中转子的位置信号由编码器获得，速度信号可以通过位置信号差分获得；电流内环中三相电流通过电流传感器获得。机械外环接收外部给定的位置和速度信号，与电机编码器反馈的转角和速度信号比较，经过速度控制器 ASR 生成转矩电流指令；电流内环接收电流指令，与电流传感器反馈的三相电流矢量变换得到的d、q轴反馈电流比较，经过电流控制器 ACR 生成d、q轴电压指令，再进行dq-abc的坐标系变换得到三相电压指令，驱动永磁电机PMSM。

在常规矢量控制中，APR、ASR和ACR为PID控制器。本文依照式(13),将APR、ASR和ACR的PID控制器修改为前馈型二自由度控制器，从而在矢量控制中引入了二自由度控制。

3 永磁同步伺服电机二自由度控制的软件仿真验证与实际应用

3.1 软件仿真验证

与直流电机单闭环调速系统不同，永磁同步伺服电机调速系统需要采用图5所述的三环控制。其中：外环为位置环，中环为速度环，内环为电流环。电流环还包括d、q轴两路电流id、iq控制，故通常需要整定4组控制器参数。在MATLAB/Simulink中，搭建永磁同步伺服电机二自由度控制仿真图，如图6所示。

仿真中，永磁同步电机参数如下：极对数4，定子电阻0.091 8 Ω，电枢电感0.975 mH，转动惯量0.003 945 kg·m2，转子磁场系数0.168 8 Wb。为了对比本文控制效果，4个PID控制器分别采用PID控制和二自由度控制两种控制方法。当采用常规PID控制时，对4个PID控制器的参数设置。位置环APR：Kp=350、Ki=150、Kd=40。速度环ASR：Kp=0.165、Ki=0.2。电流环ACR的d轴Kp=0.15、Ki=0.1。电流环ACR的q轴Kp=0.1、Ki=0.1。当采用二自由度控制时，常规PID参数不变，仅改变各环的b、c的值。它们取：位置环b=1.04、c=1.01，速度环b=1.2、c=1.05，电流环q轴b=1.05、c=1.01，电流环d轴b=1.0、c=1.0。

在给定位置参考信号为正弦波信号时验证控制器对正弦信号的跟随性能，并与采用普通PID控制的矢量控制系统进行对比，其θ-t输出特性曲线如图7所示。

图6 永磁同步伺服电机二自由度控制仿真结构

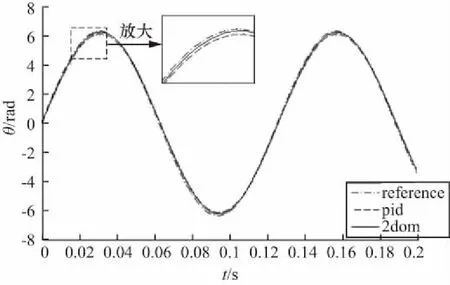
图7 永磁同步伺服调速系统对正弦信号的θ-t响应曲线

由图7可见，在永磁同步伺服控制系统中，引入二自由度控制，可以获得比常规PID控制更好的跟随性能。采用前馈型二自由度控制器，系统的干扰抑制特性只受Kp、Ki、Kd参数的影响，而跟随特性同时受Kp、Ki、Kd、b、c的影响。如果按照干扰抑制特性最优整定Kp、Ki、Kd参数，即可使系统获得良好的干扰抑制特性；同时通过调整b、c的参数，可以使系统在不改变干扰抑制特性的前提下，兼顾良好的跟随特性。因此，将二自由度控制引入永磁同步伺服电机矢量控制系统，可以使系统获得更好的调速性能。

3.2 实际应用

为了使二自由度控制器在实际工程中得到应用，本文给出了二自由度伺服控制器的设计方案。选取DSP TMS320F28335作为核心控制芯片，其指令周期为6.67 ns，主频150 MHz，具有高性能的浮点运算单元，以便于实现伺服电机的高速数字化控制。永磁同步伺服控制器的二自由度控制系统硬件结构如图8所示。

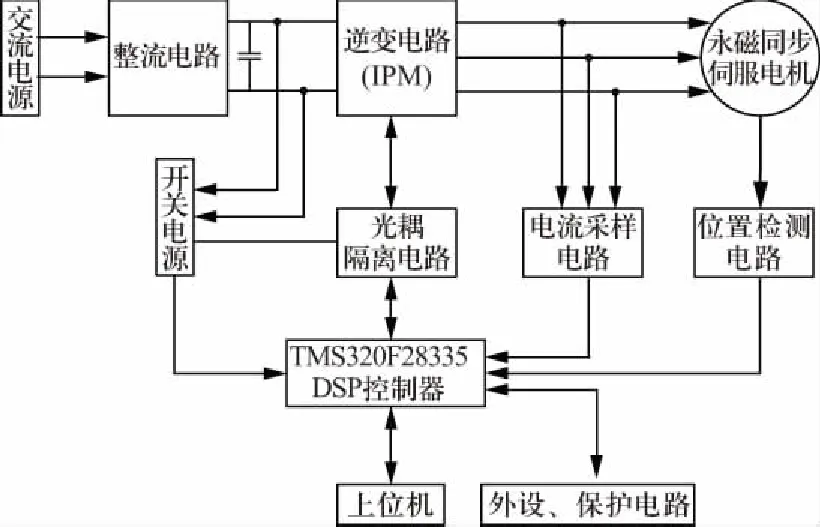
图8 永磁同步伺服控制器的二自由度控制系统硬件结构

永磁同步伺服电机二自由度控制的软件算法流程如图9所示。其位置、速度与电流控制器设计参见式(13)。

图9 永磁同步伺服控制器的二自由度控制系统软件流程

依据所述方案，本文设计了永磁同步伺服控制系统的试验平台。经试验验证，该系统的控制精度和响应速度较常规控制方法有所增强，能够更加平稳流畅地运行。

4 结 语

在永磁同步伺服控制系统中，引入二自由度控制，只需进行简单的改进，即可获得更好的控制性能。这样，与指令相关的前馈调整和与外部振动有关的反馈调整可以独立进行，从而可以缩短稳定时间和降低振动，对于实现加工制造业中电子零部件安装机器的高速化，提高金属加工机器的加工精度，具有重要意义。

【参考文献】

[1] 谢玉春. 交流永磁同步电机伺服系统控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.

[2] 薛薇. 永磁同步电机调速系统的模糊自抗扰控制[J]. 电机与控制应用, 2013, 40(8): 57-60.

[3] 黄友锐, 曲立国. PID控制器参数整定与实现[M]. 北京: 科学出版社, 2010.

[4] MINORU S, TOSHIMI S, KOJI I, et al.Two degree of freedomcontrol system for motioncontrol of a flexible stacker Ccrane[C]∥SICE Annual Conference,2008：3272-3277.

[5] 郑伟峰. 交流伺服系统无时滞反馈高响应驱动控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[6] ALFARO V M, VILANOVA R, ARRIETA O. Two degree of freedom PI/PID tuningapproach for smooth control on cascade control systems[C]∥Proceedings of the 47th IEEE Conference on Decision and Control, 2008:9-11.

[7] 张井岗.二自由度控制[M].北京:电子工业出版社,2012.

[8] 舒鑫东, 庄圣贤, 关晓明, 等. 交流永磁同步电机二自由度控制[J].电气传动,2009,39(12):54-56.

[9] 赵希梅, 郭庆鼎, 孙宜标. 永磁直线同步伺服电机的零相位二自由度H∞鲁棒跟踪控制[J].电工技术学报, 2004,19(10):34-37.

[10] TAWORN B, N S，N N. Two degree of freedom simple servo Aadaptivecontrol for SCARA Robot[C]∥International Conference on Control, Automation and Systems, KINTEX, Gyeonggi-do, Korea,2010:480-484.