关于Diophantine方程x3+64=273y2的整数解*

廖 军

(文山学院 数学学院，云南 文山 663000)

方程

x3±64=Dy2(x，y∈N，D>0，且无平方因子)

(1)

是一类重要的Diophantine方程，其整数解只有为数不多的学者研究过.目前的主要结论有：1994年，李复中[1]给出D只含一个6k+1形素数因子时不定方程x3±64=3Dy2在一些条件下无非平凡解的充分条件；同年，张海燕、李复中[2]给出D不能被3或6k+1形的素数整除且D≠k+2时，不定方程x3±64=Dy2无非平凡解的充分性条件；2008年，赵天[3]给出了不定方程x3±26=3Dy2(D=7，13，19，31)的所有整数解；2012年，张攀[4]给出了10个不定方程x3±64=py2(p=7，13，19，37，43)的所有整数解；牛芳芳、罗明[5]给出了不定方程x3-64=31y2的所有解；赵天[6]给出了不定方程x3+64=21y2的所有解.此处主要讨论Diophantine方程x3+64=273y2的解的情况.

引理1[7]不定方程x3+1=273y2仅有整数解(-1，0).

定理1 Diophantine方程

x3+64=273y2

(2)

仅有整数解(-4，0).

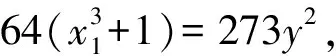
当x<≢0(mod 2)时，y<≢0(mod 2)，因为x3+64=(x+4)(x2-4x+16)，所以gcd(x+4，x2-4x+16)=1或3，从而由方程(2)可以得出下列8种可能的情形：

情形①：x+4=273a2，x2-4x+16=b2，gcd(a，b)=1，y=ab.

情形②：x+4=a2，x2-4x+16=273b2，gcd(a，b)=1，y=ab.

情形③：x+4=91a2，x2-4x+16=3b2，gcd(a，b)=1，y=ab.

情形④：x+4=3a2，x2-4x+16=91b2，gcd(a，b)=1，y=ab.

情形⑤：x+4=819a2，x2-4x+16=3b2，gcd(a，b)=3，y=3ab.

情形⑥：x+4=3a2，x2-4x+16=819b2，gcd(a，b)=3，y=3ab.

情形⑦：x+4=273a2，x2-4x+16=9b2，gcd(a，b)=3，y=3ab.

情形⑧：x+4=9a2，x2-4x+16=273b2，gcd(a，b)=3，y=3ab.

下面分别讨论方程(2)在这8种情形下的所有解的情况.

情形①，由第2式可得x=0或4，代入到第1式，可知x=0或4均不适合此式.因此在该情形下方程(2)无整数解.

情形②，因为x<≢0(mod 2)，所以a≡1(mod 2)，b≡1(mod 2)，则有a2≡1(mod 8)，b2≡1(mod 8)，由第1式得x=a2-4≡-3≡5(mod 8)，代入第2式得x2-4x+16≡21≡5(mod 8)，又因为b2≡1(mod 8)，所以273b2≡1(mod 8)，故5≡x2-4x+16=273b2≡1(mod 8)，矛盾.因此在该情形下方程(2)无整数解.

情形③，因为x<≢0(mod 2)，所以a≡1(mod 2)，b≡1(mod 2)，则有a2≡1(mod 8)，91a2≡3(mod 8)，由第1式得x=91a2-4≡-1≡7(mod 8)，代入第2式得x2-4x+16≡37≡5(mod 8)，又由于b≡1(mod 2)，则有b2≡1(mod 8)，3b2≡3(mod 8)，故有5≡x2-4x+16=3b2≡3(mod 8)，矛盾.因此在该情形下方程(2)无整数解.

情形④，因为x<≢0(mod 2)，所以a≡1(mod 2)，b≡1(mod 2)，则有a2≡1(mod 8)，b2≡1(mod 8)，由第1式得x=3a2-4≡-1≡7(mod 8)，代入第2式得x2-4x+16≡37≡5(mod 8)，又因为b2≡1(mod 8)，所以91b2≡3(mod 8)，故5≡x2-4x+16=91b2≡3(mod 8)，矛盾.因此在该情形下方程(2)无整数解.

情形⑤，因为x<≢0(mod 2)，所以a≡1(mod 2)，b≡1(mod 2)，则有a2≡1(mod 8)，819a2≡3(mod 8)，由第1式得x=819a2-4≡-1≡7(mod 8)，代入第2式得x2-4x+16≡37≡5(mod 8)，又由于b≡1(mod 2)，则有b2≡1(mod 8)，9b2≡1(mod 8)，故5≡x2-4x+16=9b2≡1(mod 8)，矛盾.因此该情形下方程(2)无整数解.

情形⑥，因为x<≢0(mod 2)，所以a≡1(mod 2)，b≡1(mod 2)，则有a2≡1(mod 8)，9a2≡1(mod 8)，由第1式得x=9a2-4≡-3≡5(mod 8)，代入第2式得x2-4x+16≡13≡5(mod 8)，又由于b≡1(mod 2)，则有b2≡1(mod 8)，819b2≡3(mod 8)，故5≡x2-4x+16=819b2≡3(mod 8)，矛盾.因此在该情形下不定方程(2)无整数解.

情形⑦，因为x<≢0(mod 2)，所以a≡1(mod 2)，b≡1(mod 2)，则有a2≡1(mod 8)，273a2≡1(mod 8)，由第1式得x=273a2-4≡-3≡5(mod 8)，代入第2式得x2-4x+16≡21≡5(mod 8)，又因为b≡1(mod 2)，则有b2≡1(mod 8)，9b2≡1(mod 8)，故有5≡x2-4x+16=9b2≡1(mod 8)，矛盾.因此在该情形下方程(2)无整数解.

情形⑧，因为x<≢0(mod 2)，所以a≡1(mod 2)，b≡1(mod 2)，则有a2≡1(mod 8)，b2≡1(mod 8)，由第1式得x=9a2-4≡-3≡5(mod 8)，代入第2式得x2-4x+16≡21≡5(mod 8)，又因为b2≡1(mod 8)，所以273b2≡1(mod 8)，故5≡x2-4x+16=273b2≡1(mod 8)，矛盾.因此在该情形下方程(2)无整数解.

从以上8种情形的讨论，可知Diophantine方程(2)无x<≢0(mod 2)的整数解.

综上所述，Diophantine方程(2)有仅有整数解(-4，0).

参考文献：

[1] 李复中.关于丢番图方程x3±64=3Dy2[J].东北师范大学报：自然科学版，1994(2)：16-17

[2] 张海燕，李复中.关于丢番图方程x3±64=Dy2[J].哈尔滨科学技术大学学报：1994，18(3)：107-109

[3] 赵天.关于不定方程x3±23n=3Dy2解的讨论[D].重庆：重庆师范大学，2008

[4] 张攀.关于不定方程x3±64=py2的研究[D].陕西：西北大学，2012

[5] 牛芳芳，罗明.关于不定方程x3-64=31y2[J].重庆文理学院学报：自然科学版，2012，31(2)：32-34

[6] 赵天.关于不定方程x3+64=21y2[J].重庆工商大学学报：自然科学版，2008，25(1)：9-12

[7] 曹玉书，郭庆俭.关于丢番图方程x3±1=3Dy2[J].黑龙江大学学报：自然科学版，1989(4)：68-71