基于可拓理论的教学质量综合评价*
2014-08-08刘小英
刘小英, 张 健
(攀枝花学院 a.数学与计算机学院;b.交通与汽车工程学院,四川 攀枝花 617000)
教学质量评价是指在全面考察教学质量的众多指标情况下,运用有效的技术手段,对教学价值做出判断[1]。目前,许多学者进行深入研究,提出了许多评价方法,例如最大熵神经网络、支持向量机算法、模糊综合评判法、BP神经网络等方法,都取得了一定的成效[2-5]。影响教学质量评价的因素众多,它是一个多层次、多指标的非线性问题,各大高校均有自己的教学质量评价指标体系,但各指标及权重均由专家经验主观确定,使教学质量评价的准确性受到影响,由于教学过程的不确定性,需要合理确定教学质量评价指标,并利用科学的方法确定评价指标权重,采用适合的决策方法做出正确的评价。
建立在关联函数计算基础上的可拓优度评价是最简单有效的评价方法之一[6]。在合理确定教学质量评价指标的基础上,采用层次分析法确定各指标的权重,采集评价数据,最后应用可拓方法对教学质量做以评价,为决策提供参考。
1 评价指标体系确定
构建合理的教学质量评价指标体系是正确对教学质量进行评价的先决条件,采用文献分析法和专家访谈法[7]结合相关高校的教学质量评教指标体系,构建的教学质量评价体系如表1所示。
2 层次分析法确定权重
对教学质量进行评价过程中,各指标权重的确定尤为重要,将会影响评价结果是否可靠。层次分析法(AHP法)是将与决策有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析,利用数学的逻辑推理,尽量剔除主观成分,使权重尽量符合客观实际[8,9]。首先对准则层各项指标通过两两比较构造判断矩阵,计算矩阵最大特征根λmax,并求出关于最大特征根的特征向量进行归一化处理后,即可得到各指标权重ω。

表1 教学质量评价指标体系
根据层次分析理论,结合教学质量评价实际,共分4个层次。教学质量为目标层A,一级指标为准则层B,二级指标为子准则层C,待评教师为方案层P。
经调研督导专家意见,认为经过多年教学,对于一名老教师来说,任教经验及对一门学科熟悉程度都应该达到一定水平,而目前高校新近教师都为高学历,科研能力较强弥补了经验少的不足,因此教师素质在教学质量重要因素中应该排在末尾,而教学态度比其略微重要。对于课堂教学质量来说,教学内容又比教学态度重要,而好的方法才能吸引学生注意,有助于学生吸收知识,所以教学方法又比教学内容重要。教学质量高的体现是学生的获得的知识和能力的提高,因此教学效果应该是教学质量评价中最重要的指标。综上所述,一级指标中教师素质、教学态度,教学内容、教学方法、教学效果重要性依次增加,对准则层(一级指标)进行比较构造两两判断矩阵,并得各一级指标权重为
ωA=(0.033 3,0.063 4,0.128 9,0.261 5,0.512 8)
同理构造子准则层判断矩阵,并计算出子准则层中各二级指标权重得
ωB1=(0.56,0.27,0.11,0.06);ωB2=(0.75,0.25);ωB3=(0.64,0.26,0.10);
ωB4=(0.75,0.25);ωB5=(0.61,0.27,0.12).
3 教学质量可拓综合评价
3.1 可拓学基础
3.1.1 物 元[10]
以物Om为对象,Cm为特征,Om关于Cm的量值Vm构成的有序三元组,作为描述事物的基本元,称为一维物元。一物具有多个特征,与一维物元相仿,可以定义为多维物元,记为
(1)
3.1.2 右侧距及关联函数
在应用优度评价法对教学质量进行评价时,督导专家然后根据实践经验对待评教师的各项指标进行打分,学生则根据个人所感对教师进行打分。分值越高证明老师某项教学效果越好,因此在涉及关联函数计算时,符合可拓理论右侧距情况。
(2)
为x与区间X0关于x0的右侧距。
(2) 关联函数及关联度计算。设X0=〈a,b〉,X=〈c,d〉,x0∈〈a,b〉,X0⊂X,最优点在x0处时的关联函数为
(3)
式(3)中,D(x,X0,X)称为位值,计算方法为
(4)

图1 评价基本流程
3.1.3 优度计算
优度是应用关联函数确定待评价对象关于衡量指标符合要求的程度,某评价等级优度值越高,证明待评案例更加符合该评价等级。优度计算公式可表示为
(5)
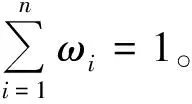
3.2 评价基本流程
应用可拓理论对教学质量进行评价基本流程如图1所示。
3.3 教学质量指标等级划分
抽取3名讲课较优秀教师参评,即P={P1,P2,P3}。经过首次评价后,根据表1中各指标进行打分。各评价特征值都被划分成优、良、中3个等级,然后划分其经典域,同一评价指标的经典域量值范围相同,并根据每个评价指标可能达到的量值确定节域。经典域为待评案例各特征的量域,节域为特征所允许的量域[11]。为方便起见,每项二级指标均已百分制计算,由督导专家打分后取平均值。教学质量衡量指标体系详见表4。
表4 教学质量指标评分一览表
3.4 建立物元模型
根据教学质量指标评分具体情况,优、良、中各等级对应的经典域分别为〈90,100〉,〈80,90〉,〈70,80〉,每个评价等级的各项指标经典域相同,节域为〈50,100〉。根据式(1),则可确定评价方案经典域物元模型M0、节域物元模型M分别为
有3名参评教师,所以待评物元模型为
3.5 计算关联函数
根据式(2)、(3)、(4)计算得出二级指标关联函数计算结果如表5所示。
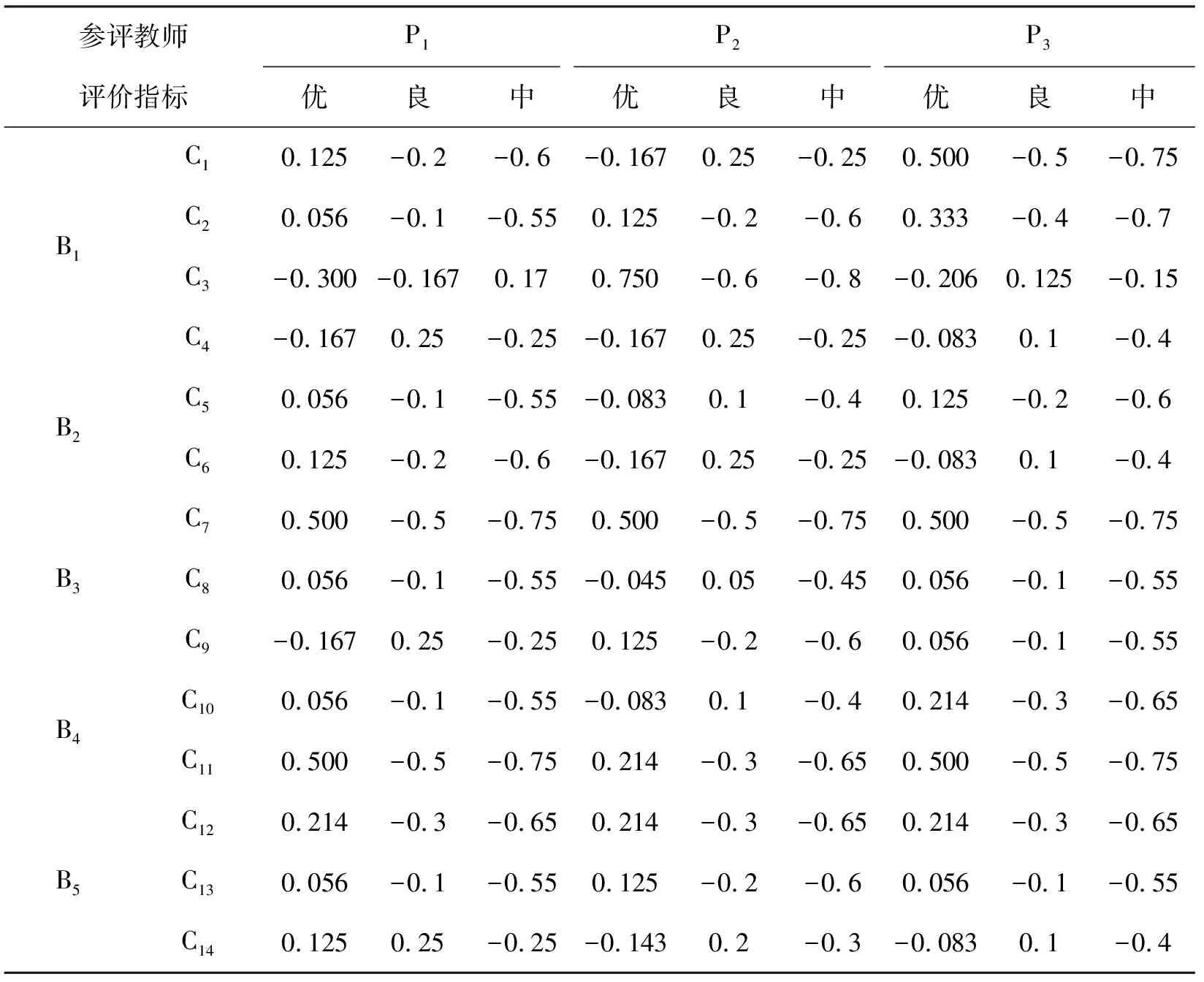
表5 二级指标关联函数计算结果
3.6 计算优度
根据前文中应用层次分析法所得各二级指标和一级指标权重,根据式(5)计算待评案例得第二层次、第一层次可拓优度评价结果如表6所示。

表6 可拓优度评价结果
3.7 教学质量评价分析
(1) 由表6中可拓优度评价结果可知,参评3名教师3个等级的优度值大小排序均是优>良>中,因此3名教师的总体评价结果均为优秀,与实际情况相符。
(2) 参评教师隶属度为优的优度值顺序由大到小排序为P1>P3>P2,因此3名教师的互相比较结果很容易得出来了。在具体应用评价结果时,在选择评价课程任课教师时,P1,P3较有竞争优势,在现在许多高校里实施的竞争上岗和承担课程准入制度有较大的实用价值。
(3) 从单项指标打分可以看出,教师P2科研能力非常强,但是根据层次分析法得出的权重比较重视教学效果,因此可以看出侧重点不同将对评价结果有一定影响。
实际选择的3名参评教师1名为副教授、攀枝花学院教学带头人,1名为副教授、博士,1名为讲师,分析的结果与实际情况相符,证明此方法有较好的可信度。
4 结 语
将可拓理论和层次分析法相结合对教学质量进行评价,可以发挥方法各自优势,进而保证评价结果的准确与公正。高校教学质量评价是一项较复杂的系统工程,在使用此方法的过程中,高校决策者应根据学校特点确定评价指标体系并重构判断矩阵,保证评价结果的科学性和有效性。
参考文献:
[1] 魏正元,颜克胜,苏盈盈.基于最大熵NN的教学质量评价模型及仿真[J].计算机仿真,2013,30(5):284-287
[2] 叶勇.基于云模型的课堂教学质量数据挖掘[J].计算机仿真,2012,29(8):373-376
[3] 李波.支持向量机在高校教学质量评价中的应用研究[J].计算机仿真, 2011,28(10):402-405
[4] 吴虹.基于模糊综合评判法的高校教师教学质量评价体系的构建[J]. 统计与决策,2010(3):166-168
[5] 孙晓玲,王宁,梁艳.应用BP神经网络的教学评价模型及仿真[J]. 计算机仿真,2010,27(11):314-318
[6] 张健,张敬东,刘小英.基于可拓工程分析法的机械设计方案决策[J]. 现代制造工程,2013(7):104-109
[7] 郑延福.高校教学质量评价指标的确定[J].统计与决策,2011(2):165-167
[8] 王化吉,宗长富,管欣,等.基于模糊层次分析法的汽车操纵稳定性主观评价指标权重确定方法[J].机械工程学报,2011,47(24):83-90
[9] 王 俊,谢晓佳. 基于层次分析法及可拓理论的露天采石场安全评价[J].重庆工商大学学报:自然科学版,2013,30(6):61-68
[10] 杨春燕,蔡文.可拓工程[M].北京:科学出版社,2007
[11] 焦爱胜,易湘斌,严慧萍.机械加工工艺方案的可拓评价研究[J].机械科学与技术,2009,28(11):1482-1485
