关于不定方程x2+64=y11的解的讨论
2014-08-08安晓峰
安 晓 峰
(重庆师范大学 数学学院,重庆 401331)
A,B∈N,A无平方因子,关于不定方程Ax2+B=yn(其中x,y∈N,n≡1(mod2),n>1) 的解的讨论是数论中的一类重要课题.近来文献[1-5]用代数数论的方法证明了几种不同方程的整数解,而A=1,B=64,n=11的情况未曾讨论.为此,利用代数数论的方法证明了不定方程x2+64=y11无整数解.
定理1 不定方程
x2+64=y11,x,y∈Z
(1)
无整数解.
证明先假设x≡1(mod2),在Z[i]中,式(1)可以写成(x+8i)(x-8i)=y11,x,y∈Z.
设δ=([x+8i],[x-8i]),由δ|([2x],[16i]),知δ只能取[1],[1+i],[2],因x≡1(mod2),知x+8i≡1(mod2),所以δ≠[2];如果δ=[1+i],则N(1+i)|N(x+8i),即2|x2+64,但这与x≡1(mod2)矛盾,因此δ=[1].
由Z[i]唯一分解性得到x+8i=(a+bi)11,x,a,b∈Z,因而有
x=a11-55a9b2+330a7b4-462a5b6+165a3b8-11ab10
(2)
8=b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10)
(3)
因此b=±1,±2,±4,±8.
当b=±1时,由式(3)可得
11a2(a8-15a6+42a4-3a2+5)=9,-7
(4)
式(4)要成立,要满足11|9,11|-7,矛盾.
当b=±2时,由式(3)可得
4(±1+28)=11a10-165a8·22+462a6·24-330a4·26+55a2·28
(5)
即得
4(165a8+28±1)=11a2(a8+42a4·24-30a2·26+5·28)
(6)
式(6)要成立,需满足11|165a8+28±1,矛盾.
当b=±4时,由式(3)可得
2(±1+219)=11a10-165a8·42+462a6·44-330a4·46+55a2·48
即
2(±1+219-180 224 0a2)=11a2(a8-15a6·42+42a4·44-30a2·48)
(7)
式(7)要成立,需满足11|±1+219-180 224 0a2,矛盾.
当b=8时,由式(3)得
1=11a10-165a8·82+462a6·84-330a4·86+55a2·88-810
即
810+1=11a2(a8-15a6·82+42a4·84-30a2·86+5·88)
(8)
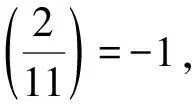
当b=-8时,由式(3)得-1=11a10-165a8·82+462a6·84-330a4·86+55a2·88-810,即a10-15a8·82+42a6·84-30a4·86+5a2·88=97 612 893,从而有
a2(a8-15a4·82+42a6·84-30a2·86+5·88)=32×7×31×151×331
(9)
式(9)要成立,需满足a=±1,±3,而当a=±1时,a10-15a4·82+42a6·84-30a2·86+5·88≠97 612 893,此时无整数解.同理,当a=±3时也无整数解.所以当x≡1(mod2)时,式(1)无整数解.
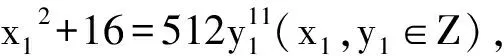
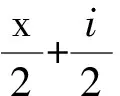
当μ=[1]时,i(i-1)10=25一定只能整除[x2+i]或[x2-i]中的一个,但x2为奇数,从而不成立,所以25不能整除[x2+i]或[x2-i],故μ≠[1],所以μ=[1-i].因此式(1)可化为
由Z[i]是唯一分解环,可令x2+i=(1+i)5(a+bi)11(a,b∈Z),可得
(10)
(11)
显然式(11)不成立,故此种情况,式(11)无整数解.
综上讨论结果,不定方程x2+64=y11,x,y∈Z无整数解.
参考文献:
[1] 高媛媛,郭金保. 关于不定方程x2+64=y5[J].延安大学学报:自然科学版,2010,29(1):6-7
[2] 张杰. 关于不定方程x2+64=y7的解的讨论[J].重庆工商大学学报:自然科学版,2012,29(3):27-28
[3] 高丽,马勇刚. 关于不定方程x2+16=y7[J].西南民族大学学报:自然科学版,2008,34(1):27-29
[4] 李娜. 关于不定方程x2+4=y7[J].科学技术与工程,2011,23(11):5613-5614
[5] 李中恢,张四保. 关于不定方程x2+16=y11[J].海南大学学报:自然科学版,27(3):216-218
