6 MV医用加速器电子对效应的蒙特卡罗模拟研究

孔 栋，顾思毅，倪 婕，孙 亮,*

(1.苏州大学医学部 放射医学与防护学院，江苏 苏州 215123；2.苏州大学附属第一医院，江苏 苏州 215006)

对于肿瘤的放疗，尤其是深部肿瘤的放疗，当前主要利用医用直线加速器所产生的X射线。X射线产生的主要原理是高速运动的电子从原子核附近掠过时，在原子核库仑场作用下，电子运动方向和速度发生变化，其一部分动能转变为连续能谱的X射线[1]。加速器中经过均整器和准直器等修正后的X射线作用于人体，可使肿瘤部位得到足够高的剂量，从而治疗肿瘤。X射线在到达人体前与机头各部件及周围空气介质发生了多种相互作用，其中电子对效应[1]在一定程度上改变了X射线射野内的能谱分布和注量率，并增加了射野中电子和正电子的注量率，很多学者致力于污染电子的产生规律[2-4]和减少其到达人体皮肤表面方法[5-8]的研究，但很少有人关注电子对效应在其中的作用。关于加速器射束中正电子的存在文献[9-11]中已有报道，且付廷岩[11]通过Geant4模拟得到了医用直线加速器射束的相空间文件，并分析给出了射束中正电子的能谱分布。正电子在能量耗尽后会与介质中的电子结合发生湮没辐射[12]，释放出两个能量为0.511 MeV的湮没光子，张翼等[13]利用轫致辐射X射线与物质发生电子对效应所产生的正电子的湮没辐射对样品进行了分析，其通过湮没辐射光子研究电子对效应的思想对本研究有重要启发。在放疗和辐射防护中应对电子对效应加以考虑，但目前国内外很少有针对医用电子直线加速器开展这方面的研究，因此，本文应用蒙特卡罗程序包Geant4[14]对6 MV医用加速器中电子对效应进行研究。

1 实验

1.1 实验设备

SIEMENS Primus Plus加速器；IBA三维水箱；计算机操作系统为32位Win7，CPU为Intel(R) Core(TM)i7-2600，主频为3.4 GHz；编译环境为Visual Studio 2010；Geant4程序(版本号9.6)。

1.2 模型建立与参数设定

依据医院和生产厂家提供的信息，编程构建源皮距(SSD)为100 cm，射野依次为5 cm×5 cm、10 cm×10 cm、15 cm×15 cm、20 cm×20 cm的加速器机头模型。本模型结构主要包括靶、初级准直器、均整器、监控电离室、反射镜、上准直器、下准直器、光野十字线等。图1所示为构建的10 cm×10 cm射野的加速器机头模型，其他与此类似，不同之处主要在于次级准直器开口的大小。在靶后、均整器前、均整器后、反射镜后、下准直器后及SSD处6个层面记录粒子的相空间文件，各层面位置如图1所示。所构建加速器各部件的详细情况列于表1。

图1 加速器机头模型

本文中采用的初始电子是在半径为1 mm的圆内垂直均匀入射的单能电子。为选择合适的初始电子能量及保证所构建加速器机头模型的正确性，在另一程序中构建了30 cm×30 cm×30.5 cm的水模，在水模中心轴不同深度处及10 cm深度处y轴上设置体素，以记录相应体素的剂量值，从而计算相应的百分深度剂量(PDD)和离轴比(OAR)，通过与测量值进行比较，以调整模型的相关参数。依据水模中能量沉积特点，不同位置处体素大小设置也不同，对于10 cm×10 cm射野，体素设置如图2所示，体素大小列于表2。

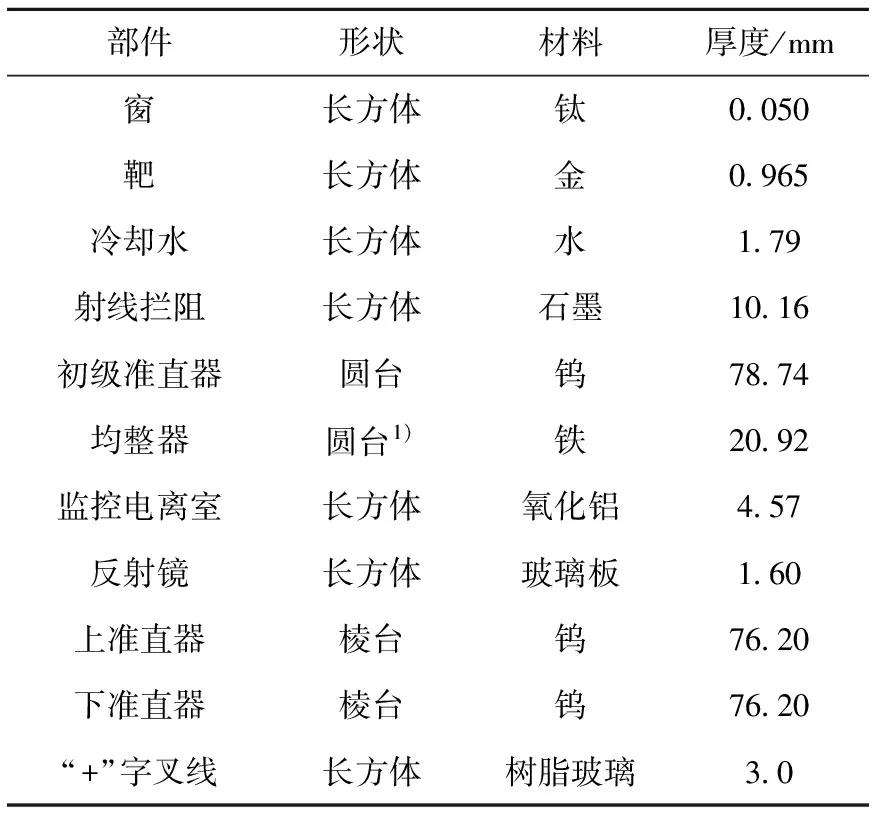
表1 Geant4中加速器机头各部件情况

注：1) 本文中均整器是由8层圆台叠加而成，其材料应为不锈钢，但因成分不明，所以用铁代替

a——沿x轴方向视图；b——沿z轴方向视图

表2 水模中体素大小

1.3 蒙特卡罗模拟

物理过程考虑了光子、电子和正电子3种粒子，光子考虑了光电效应、康普顿散射、电子对效应、瑞利散射过程；电子和正电子考虑了多重散射、电离、轫致辐射及正电子湮没等。本文中所有物理过程均设为Penelope模型，3种粒子截止范围均设为1 mm。

在SSD为100 cm，射野为10 cm×10 cm下，分别获取了初始电子能量为5.8～6.5 MeV时SSD水平的相空间文件，以此作为粒子源，通过坐标转换将其置于水模表面，模拟水模中的剂量分布，通过与测量的PDD比较，选择合适的入射电子束能量，使两者相差小于2%。获得合适的能量值后，通过调整各部件参数，尤其是均整器的参数，使模拟与测量的OAR相差小于2%。除剂量较小处外，水模中各点剂量统计相对偏差均控制在1%以内。

本文针对上述4个常用的射野分别进行模拟，每次模拟分8组，每组运行电子数为2.25×108。各组分别记录靶后、均整器前、均整器后、反射镜后、下准直器后、SSD处6个层面的粒子相空间信息，生成相应的相空间文件，随后将相同射野下各组相同层面相空间文件融合，得到该射野6个层面总的相空间文件，后续的分析均基于这些相空间文件。

2 结果和讨论

2.1 模拟值与测量值的比较

图3示出SSD为100 cm，射野为10 cm×10 cm时6 MV X射线PDD和OAR模拟值与测量值的比较，测量值由IBA三维水箱测得。考虑到表面污染电子的影响[15-16]，模拟PDD和OAR时以中心轴10 cm深度处剂量作为归一点[17-18]。从图3a可看出，模拟与测量的PDD值符合很好，超过最大剂量深度的区域，它们之间最大相对偏差小于2%，因此，选定的初始电子束能量6.2 MeV是合理的；由图3b可见，距中心轴-5.5 cm～+5.5 cm内，模拟与测量的OAR值最大相对偏差小于2%，因此，本文中加速器模型的构建是合理的，模拟结果可信。引起上述差异的原因有：加速器机头模型构建不够精细，一些细节问题尚需完善；Geant4模拟过程中会产生一定的统计误差；水模周围环境设置与测量时不一致；使用三维水箱测量中会有误差。

2.2 电子对效应的产生

图4为SSD水平不同射野在30 cm×30 cm范围内所得粒子的能谱情况，某射野下的相对注量指对应射野下该能量区间的入射粒子数相对于总入射粒子数的百分比。统计不同能量区间的粒子数时，能量间隔为0.01 MeV，各样点能量为所在区间的中间值。能量在0.1～5.0 MeV之间的各区间，粒子数相对偏差小于1%。由图4可看出，对于不同的射野，0.51～0.52 MeV区间均是峰值区间。加速器中X射线的产生是由于轫致辐射，轫致辐射谱是连续的[1]，已知湮没光子能量为0.511 MeV，据此可知这些点的出现是由于发生了湮没辐射。表3列出图4中能谱峰值区间的模拟结果及其插值结果，表4列出相空间文件中电子和正电子的相对注量。由图4和表3可看出，射野面积越小，峰值越突出，其与插值间的偏差越大，即湮没光子越多，因此电子对效应越多；由表4可知，射野面积越小，则该射野下射束中电子和正电子的相对注量越大，可推断此时的湮没辐射应更多。

图3 模拟与测量的PDD(a)和OAR(b)的比较

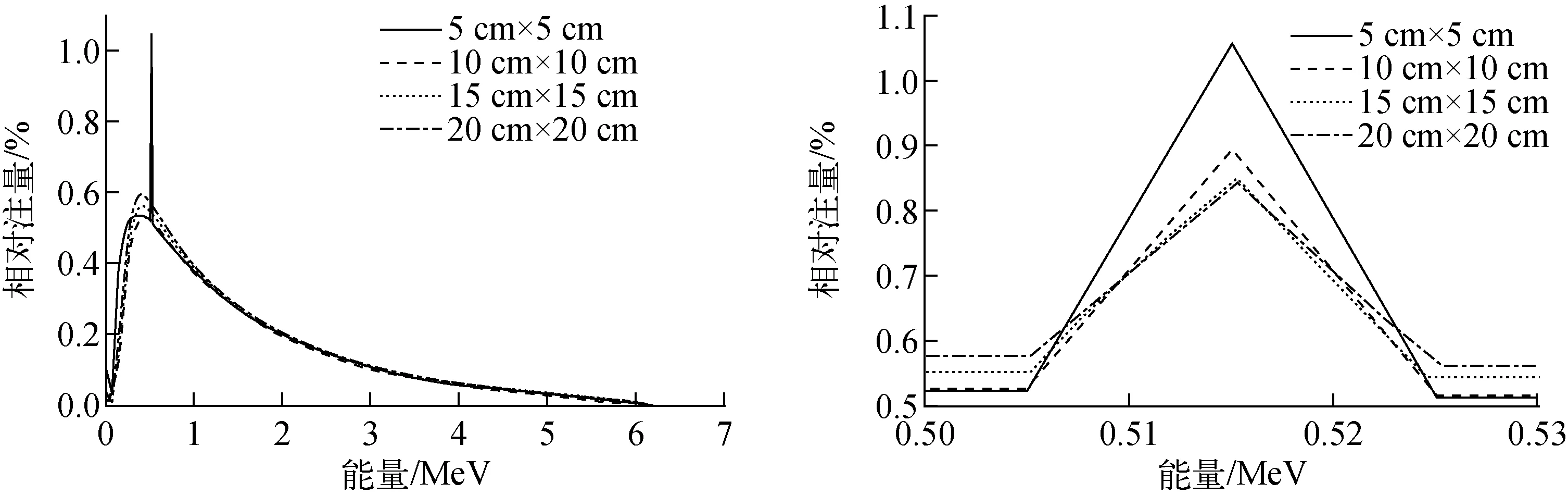
图4 SSD水平不同射野的能谱

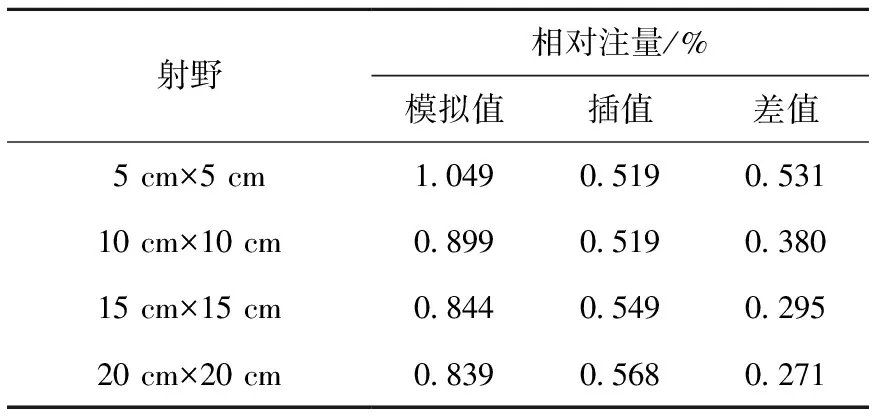
表3 不同射野峰值区间模拟及插值相对注量

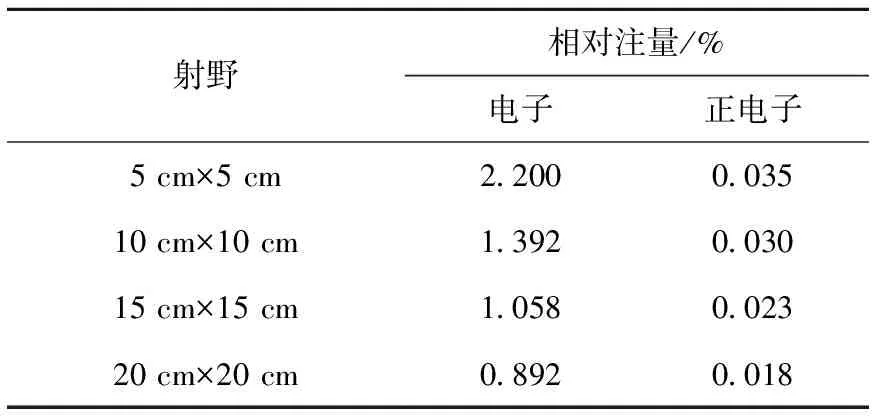
表4 不同射野电子和正电子相对注量

图5为10 cm×10 cm射野下去除各层面相空间文件中反散射粒子后所得的不同层面的能谱，能量间隔及能量在0.1～5.0 MeV范围内各区间粒子数的偏差与图4相同。由图5可见，在各层面均会出现峰值区间。由图5a可知，电子打靶产生X射线后，X射线与靶通过电子对效应产生正电子，这些正电子与靶介质相互作用能量很快耗尽，并与附近原子核外电子相互作用产生湮没辐射；图5c较图5b峰值区间粒子相对注量略高，可知射线在通过均整器过程中会发生一定的湮没辐射；图5e峰值区间粒子相对注量较图5d高很多，可知射线在通过次级准直器(包括上准直器和下准直器)时会发生较多的湮没辐射；图5f为射线束通过加速器机头各部件及环境介质后最终到达SSD处的情况，在该过程中能量较低的粒子相对注量有所减小，峰值区间的粒子相对注量下降十分明显，这一方面是由于低能粒子易于与周围介质发生相互作用从而发生散射，另一方面是由于峰值主要源于湮没辐射，这部分光子的方向本身非常分散，因此其到达SSD水平记录层面的数量明显减少。

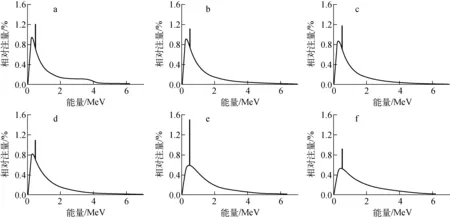
a——靶后；b——均整器前；c——均整器后；d——反射镜后；e——下准直器后；f——SSD处

2.3 电子对效应的影响

MV级X射线最大能量沉积点一般在皮肤下数厘米[19]，如本文中的6 MV X射线在水模中最大能量沉积点深度为1.6 cm，但由于污染电子的存在增加了皮肤剂量，很多学者致力于去除放疗中污染电子的研究[5,8,20-21]。电子对效应中正、负电子的能量分配和角分布满足相同的规律[1]，因此可假定由电子对效应产生的正电子和负电子到达SSD处记录层面的注量、能量及角分布是相同的，由表4可知，对于不同射野，正电子约占电子总量的2%，因此电子对效应使污染电子增加了约4%，采取一定措施减少电子对效应的发生可在一定程度上减少污染电子，同时去除污染电子的一系列方法，如对射束增加偏转电磁场[20]、在病人体表放置氮气袋[21]等，也可减少电子对效应的影响。

低能光子也是造成皮肤剂量过高的一个原因。电子对效应减少了射束中高能光子的量，而随后的正电子湮没辐射生成了低能光子(0.511 MeV)，使低能光子相对注量增加，从而降低了光子的平均能量。表5列出了不同射野下SSD层面光子平均能量的模拟值及去除湮没光子后的值。由表5可看出，在不考虑湮没光子时，平均能量提高了约0.2%，考虑到所去除的湮没光子最初是由更高能量的光子转化而来的，减少电子对效应的发生将进一步提高光子的平均能量。图3a中虚线是由SSD水平相空间文件中0.50～0.52 MeV区间光子造成的水模中PDD的分布，可看出，该能量段光子剂量主要沉积在浅表层，约在0.5 cm处达到最大值，之后迅速下降，这种特点导致了其对皮肤剂量尤其是浅表层剂量贡献较大，对深部肿瘤贡献不足。

表5 SSD层面不同射野模拟值及去除湮没光子后光子平均能量比对

图6为10 cm×10 cm射野SSD处相空间文件记录的多种粒子角分布，其中总粒子角分布考虑了所有光子和电子。由图6可见，0.5～0.52 MeV光子角分布较总的粒子角分布分散，图3b中虚线所示为这些光子在水模中10 cm深度处所致的OAR，其在射野内的波动性是由于统计粒子数较少，误差较大所致，射野外则一致性地高于测量值和模拟值。至于正电子，其角分布更加的分散。因此电子对效应增加了射野外的剂量，这增加了放疗中靶区周围正常组织的危险性，在病人体表靶区周围放置超过0.5 cm厚的组织替代物可有效减少电子对效应引起的射野外剂量。

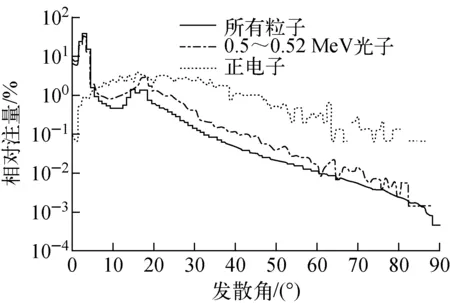
图6 粒子角分布

3 结论

本文以正电子和湮没光子作为指标探讨了电子对效应的产生及其影响。随着射野面积的减小，电子对效应的产生会增多；加速器机头多个部件会影响电子对效应的产生，其中次级准直器的影响显著。由于电子对效应的产生，X射线平均能量轻微降低，X射线变软，粒子角分布更加发散，污染电子增加了约4%。

参考文献：

[1] 胡逸民. 肿瘤放射物理学[M]. 北京：原子能出版社，1999.

[2] BIGGS P J, RUSSELL M D. An investigation into the presence of secondary electrons in megavoltage photon beams[J]. Phys Med Biol, 1983, 28(9): 1 033-1 043.

[3] NILSSON B. Electron contamination from different materials in high energy photon beams[J]. Phys Med Biol, 1985, 30(2): 139-151.

[4] MARTIN J B, TSANG C, PETER K N, et al. Simulation and measurement of air generated electron contamination in radiotherapy[J]. Radiation Measurements, 2000, 32: 105-111.

[5] LI X A, ROGERS D W O. Reducing electron contamination for photon beam-quality specification[J]. Medical Physics, 1994, 21(6): 791-797.

[6] BUTSON M J, WONG T P, LAW A, et al. Magnetic repulsion of linear accelerator contaminates[J]. Medical Physics, 1996, 23(6): 953-955.

[7] MARTIN J B, TSANG C, PETER Y, et al. Evaluation of a radiotherapy electron contamination deflecting system[J]. Radiation Measurements, 2000, 32: 101-104.

[8] WU J M, YEH S A, HSIAO K Y, et al. Far infrared for decreasing surface radiation dose of phantom with EBT film dosimetry[J]. Nuclear Instruments and Methods in Physics Research A, 2011, 652(1): 701-704.

[9] 陈朝斌，黄群英，吴宜灿，等. 蒙特卡罗方法在放疗计划中的应用[J]. 核技术，2006，29(1)：22-28.

CHEN Chaobin, HUANG Qunying, WU Yican, et al. Application of Monte Carlo techniques in radiation treatment planning[J]. Nuclear Techniques, 2006, 29(1): 22-28(in Chinese).

[10] 程品晶，王宇，凌球. 医用直线加速器治疗头的蒙特卡罗模拟[J]. 核电子学与探测技术，2009，29(1)：105-107.

CHENG Pinjing, WANG Yu, LING Qiu. Monte Carlo simulation for the therapy head of a medical linac[J]. Nuclear Electronics & Detection Technology, 2009, 29(1): 105-107(in Chinese).

[11] 付廷岩. 放射治疗中的剂量研究[D]. 兰州：兰州大学，2013.

[12] 卢希庭. 原子核物理[M]. 北京：原子能出版社，2000.

[13] 张翼，杨祎罡，李元景，等. 利用轫致辐射X射线进行正电子分析的研究[J]. 核电子学与探测技术，2011，31(4)：373-377.

ZHANG Yi, YANG Yigang, LI Yuanjing, et al. A new method of positron analysis with bremsstrahlung-induced X-ray[J]. Nuclear Electronics & Detection Technology, 2011, 31(4): 373-377(in Chinese).

[14] Geant4 Collaboration. Geant4 user’s guide for application developers[R]. [S.l.]: [s.n.], 2012.

[15] CHETTY I J, CURRAN B, CYGLER J E, et al. Report of the AAPM task group No. 105: Issues associated with clinical implementation of Monte Carlo based photon and electron external beam treatment planning[J]. Med Phys, 2007, 34(12): 4 818-4 853.

[16] ABDEL-RAHMAN W, SEUNTJENS J P, VERHAEGEN F, et al. Validation of Monte Carlo calculated surface doses for megavoltage photon beams[J]. Med Phys, 2005, 32(1): 286-298.

[17] 时颖华，周凌宏，刘迎军，等. 6 MV医用电子直线加速器的蒙特卡罗模拟[J]. 中华放射医学与防护杂志，2011，31(2)：220-224.

SHI Yinghua, ZHOU Linghong, LIU Yingjun, et al. Monte Carlo simulation of 6 MV medical electron linear accelerator[J]. Chinese Journal of Radiological Medicine Protection, 2011, 31(2): 220-224(in Chinese).

[18] 林辉，吴东升，李国丽，等. Varian 2300C直线加速器6 MV-X线的蒙特卡罗模拟[J]. 原子核物理评论，2008，25(3): 254-258.

LIN Hui, WU Dongsheng, LI Guoli, et al. Simulating Varian 2300C 6 MV-X beam by Monte Carlo code[J]. Nuclear Physics Review, 2008, 25(3): 254-258(in Chinese).

[19] GOLDSCHMIDT H, BRENEMAN J C, BRENEMAN D L. Ionizing radiation therapy in dermatology[J]. Journal of American of Dermatology, 1994, 30(2): 157-182.

[20] LING C C, SCHELL M C, RUSTGI S N. Magnetic analysis of the radiation components of a 10 MeV photon beam[J]. Medical Physics, 1982, 9(1): 20-26.

[21] YORKE E D, LING C C, RUSTGI S. Air-generated electron contamination of 4 and 10 MeV photon beams: A comparison of theory and experiment[J]. Physics in Medicine and Biology, 1985, 30(12): 1 305-1 314.