断电停机过渡过程中核主泵气液两相流动特性研究

王秀礼，王 鹏，袁寿其，朱荣生，付 强

(江苏大学 流体机械工程技术研究中心，江苏 镇江 212013)

核主泵与普通泵的最大区别在于强调压力边界的完整性和在特殊工况下的可运行性，故对核主泵的可靠性和安全性提出很高的要求。一回路的管路任何一处出现破裂导致失水事故时，管路内冷却剂的流失会导致压力发生变化，高焓冷却剂迅速变成蒸汽和水的混合物，这种两相混合物会严重影响核主泵的性能，影响泵送冷却剂到反应堆堆芯的能力。尤其是在全厂断电或核主泵电源切断，主泵转速下滑及冷却剂流量减少时，气液两相混合物会进一步导致堆芯传热恶化，燃料棒温度升高，冷却剂温度和压力也随之上升，严重影响核主泵安全可靠运行。

国内外不同研究者采用数值模拟或试验方法对核主泵的变工况进行了大量研究。Ornahen等[1]采用数值模拟与试验测量的方式模拟了核主泵紧急启动的整个过程，并确认其启动程序完全符合核电站的安全规程。Gao等[2]对核主泵在停机过程中的瞬态过程进行了数值模拟和试验研究。刘夏杰等[3]针对核主泵断电惰转过程中的瞬态水力特性进行了试验研究。Araya[4]对核主泵发生断电事故后在3种不同转动惯量下的瞬态特性进行了定量研究，研究结果表明较大的泵转动惯量可减轻事故的后果，有利于改善反应堆的安全性。Tsukamoto等[5-6]对水泵快速启动和停机瞬态过程进行试验研究和数值计算，分析了瞬态过程的性能和稳态性能的区别。Lefebvre等[7]在一闭式试验台上进行了启动试验，启动时间约为0.6 s，通过控制全过程流量的方式测试启动过程的转速和扬程。傅天清等[8]以试验研究为基础，论述了在失压工况下泵的瞬变工况、泵上下游管系内的瞬变流动特性及系统上游压头和管系长度对失控工况系统特性的影响。黎义斌等[9-10]针对一离心泵内部流场进行数值计算，在分析变工况离心泵内部流场的基础上，提出离心泵径向力数值预测的数学模型。

本文采用数值模拟与试验验证相结合的方法，研究核主泵在断电停机过渡过程中不同含气量对核主泵内部流动特性的影响。

1 数值模拟

1.1 计算模型

计算模型为AP1000核反应堆冷却剂泵。输送介质为清水，叶片数为5、导叶片数为11，蜗壳为环形结构。核主泵的性能参数列于表1。

表1 核主泵性能参数

1.2 网格划分及无关性验证

采用三维造型软件PROE生成计算区域，利用CFX前处理网格划分软件ICEM-CFD划分网格，整个计算区域均使用六面体结构化网格，计算区域包括进口水段、叶轮、蜗壳、导叶和出水段。计算区域及网格划分如图1所示。

网格无关性检查通过改变网格的尺度来实现，计算过程中逐步减少网格尺度。为确定网格数、网格疏密程度对实际计算的影响，选取8种网格数进行模拟，给出计算扬程与实际扬程的比值H′(无量纲扬程)随网格数变化的规律，结果如图2所示。由图2可知，核主泵的无量纲扬程随网格数的增加而趋于平稳，故最终确定网格数为1 282 188。

图2 网格数与扬程的关系

1.3 边界条件

以稳态计算结果作为非稳态计算的初始条件，非定常数值模拟总时间设为11 s，为了保证结果的可靠性，在定常计算的基础上先运行1 s后再监测内部流动规律，出口条件为给定压力，通过改变进口速度与转速进行模拟。

1.4 湍流模型

采用欧拉-欧拉两相流模型对核主泵在断电停机过渡过程中的气相及液相进行描述。为简化研究，本文中的两相流模型满足以下假设：1) 液相为连续不可压缩，气相为离散不可压缩，各相的物理特性均为常数；2) 核主泵中的流动为非定常流动，且主相为液相，第2相为气相；3) 假设气相为圆球形，不考虑气相的重力，且在整个过程中气相为球形，不考虑相变。

2 计算结果与分析

2.1 叶轮内部气体体积分数的分布

图3示出核主泵内部气相的变化。从图3可看出，在正常工况下(t/T=0，其中t为每个相发生的时间，T为总时间)核主泵内部的气体体积分数Cg分布较均匀，仅由哥氏力对流体的作用导致在叶轮工作面及导叶背面出现差异。在t/T=0.1时，由于流量的减少与转速的降低，液体受到叶片的夹持程度开始减弱，导致在叶轮背面附近产生旋涡。旋涡的存在使气相区域变大且相应的气体体积分数增加，与之相对应的是导叶与泵体内的气体体积分数相应降低。随着旋涡的增加与移动，叶片背面附近积聚的气相区域及气体体积分数也相应经历逐渐增大的过渡过程(t/T=0.2～0.5)。在此过渡过程中，由于旋涡的差异性，导致叶轮气相区域与气体体积分数也具有明显的差异性，最终使得泵体内的气体体积分数也具有明显的不均匀性。同时，由于流量减少至一定程度后，在泵体出口出现一较大旋涡，从而导致泵体出口处聚集大量气相区域。随着流量和转速的进一步减少和降低，叶轮进行转换能量的能力减弱，同时，由于叶轮内相应气体含量比例的增加，叶轮只能带动气体旋转，而气体单位体积的质量很小，产生的离心力不大，无法排出叶轮内部的气体。故随着t/T的增加，叶轮内的气体含量增大，泵体内的含气量明显减小。

图3 停机过渡过程中气相的变化

图4示出叶轮内的气体体积分数Cg随流量的变化。由图4可看出，随着流量的减少，不同含气量对应叶轮内气体体积分数的变化曲线不同。流量减少至设计工况的0.35倍(0.35Q′)时，含气量为10%的叶轮内气体体积分数先达到最大值后呈离散状回旋下降。流量减少至0.28Q′时，含气量为20%的叶轮内的气体体积分数达到最大值并开始呈离散状波动下降。而含气量为30%时，叶轮内的气体体积分数随流量的减少而增加，仅在小流量工况下出现回旋波动。

图4 叶轮流道内气体体积分数随流量的变化

图5示出核主泵叶轮圆周方向气体体积分数Cg的变化。从图5可看出，叶轮周向气体体积分数从t/T=0起开始增加，在t/T=0.5左右达到最大值后开始下降。此变化趋势与图2的变化趋势一致。从图5中还可看出，t/T较小时叶轮周向的气体体积分数分布不均匀，随着t/T的增加，叶轮周向气体体积分数开始趋于周期规律性。

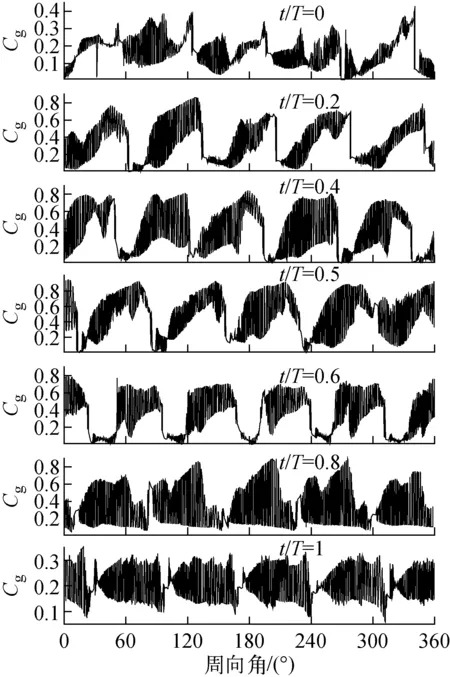
图5 叶轮周向气体体积分数的变化

2.2 各监测点气体体积分数的变化

为分析断电停机过渡过程中气液两相流动特性，在叶轮流道内设置4个监测点，如图6所示，各监测点均位于叶轮流道中间位置。

图6 叶轮内各监测点示意图

图7示出各监测点对应的气体体积分数随流量的变化。由图7可知，不同含气量在断电停机过渡过程中对不同监测点的气体体积分数的变化影响不同。不同含气量下，监测点Y1的气体体积分数的变化完全不同。含气量为10%和20%时，Y2的气体体积分数的变化趋势一致，但明显区别于含气量为30%时的变化趋势。不同含气量对Y3和Y4的气体体积分数的影响不大，其差异仅表现在脉动幅度与气体体积分数大小略有差别。故在断电停机过渡过程中，气体体积分数在靠近叶片进口处受到的影响较大。当含气量为10%时，从设计工况Q′减少至0.55Q′的过渡过程中，由于旋涡的存在，Y1出现较大的波动幅度。随着转速与流量的陡降，Y1处的气体体积分数出现陡降后又回旋波动式急剧上升，最终在小流量区域回旋波动。Y2～Y4的气体体积分数的变化趋势与扬程的类似，随着流量的减少，呈现近似指数函数关系下降并在小流量附近出现迂回波动。

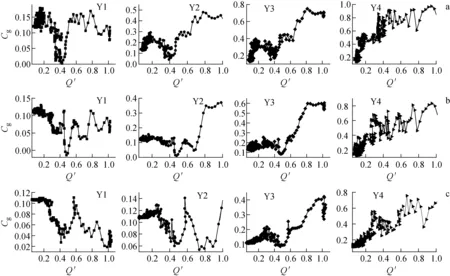
含气量：a——10%；b——20%；c——30%

2.3 各监测点流速的变化

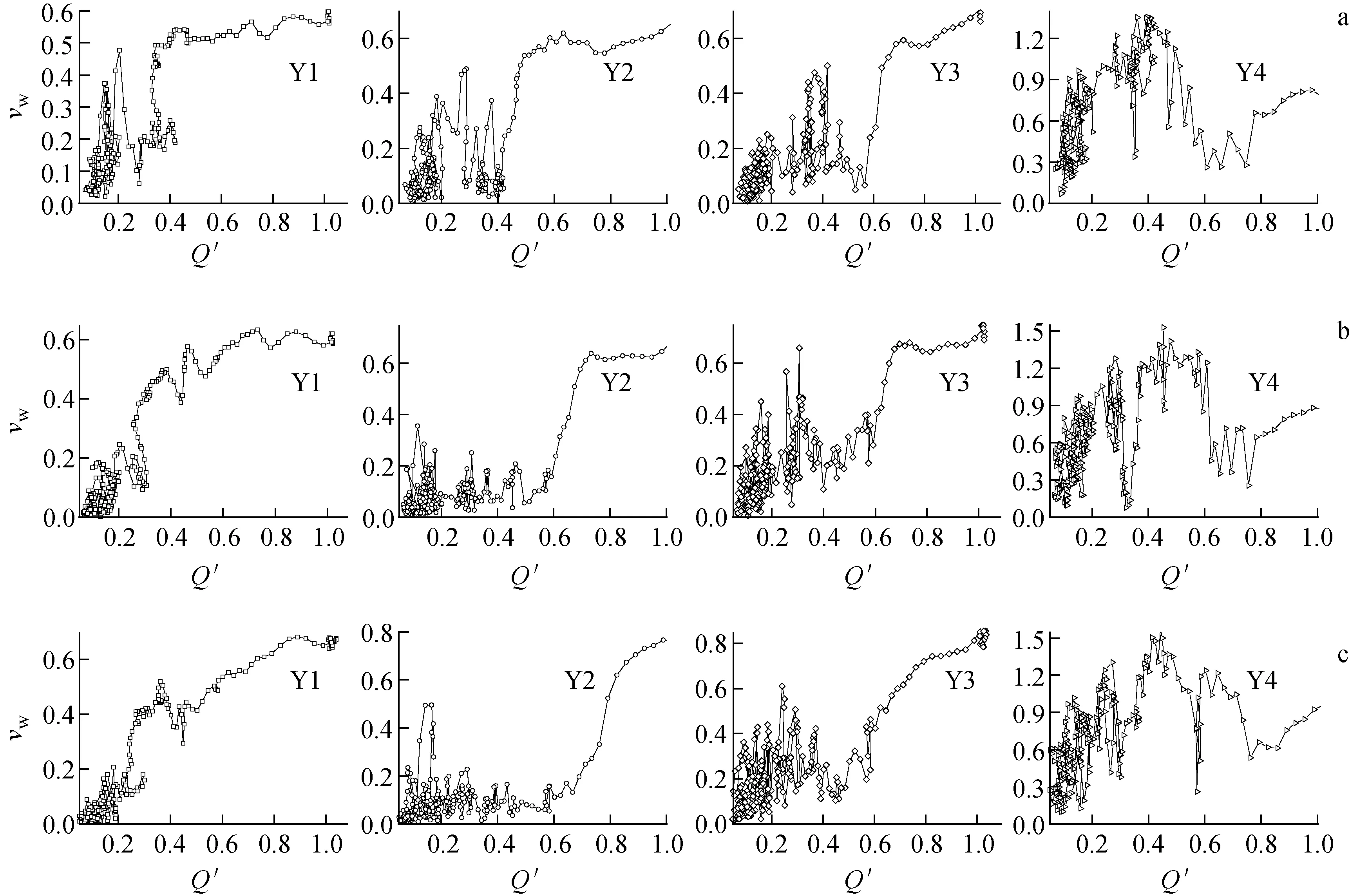
图8示出不同含气量工况下液体流速随流量的变化。图中vw为监测流速与设计工况下叶轮出口处流速的比值，为无量纲。在含气量为10%时，随流量的增加，流速先增加，再陡降，再急剧增加，其余3个监测点的流速变化规律类似，仅在小流量时出现波动。其原因在于，随着流量的减少，在叶轮出口附近出现旋涡，进而影响Y4处流速的变化。随着流量的进一步减少，旋涡开始向叶轮进口方向移动。对比图8可知，各监测点的流速在叶轮出口处出现陡降。当含气量为20%时，随着流量的减少，Y2和Y4处的流速出现急剧下降并无规律波动。造成这种现象的原因是Y4处的急剧波动主要是由于流量的减少而产生的旋涡造成。Y2处的急剧波动主要是由于随着流量的减少在叶轮进口附近聚集大量的气相而造成。当含气量增加至30%时，各监测点的流速并未出现急剧下降的趋势，除因旋涡造成的波动外，各监测流速均呈线性下降趋势。综合对比可知，在断电停机过渡过程中，含气量的变化对叶轮流道内的流速影响较大。

2.4 叶轮径向力的变化

断电停机过程中，气液两相的存在会对叶轮径向力产生影响。径向力变化会对核主泵主轴产生较大扰度，会使轴因疲劳而破坏，甚至使密封环和轴套发生研磨而损坏。故在断电停机过渡过程中，对核主泵叶轮的径向力研究十分必要。

含气量：a——10%；b——20%；c——30%

图9示出含气量对叶轮径向力Fr的影响。叶轮的径向力主要受到核主泵内部的动态循环分量(流速和压力等)的影响。在设计工况下，核主泵泵体内介质流速和流出叶轮与导叶的流速(方向和大小)基本上是一致的，从叶轮流出的介质能平顺地通过导叶而流入泵体，使叶轮周围介质的速度和压力分布较为均匀，叶轮、导叶及泵体内几乎无动态循环分量。因此，在设计工况下，核主泵叶轮主要受到泵体出口因素的影响产生向下的径向力。但在气液相工况下，气相的存在会改变核主泵内的流速和压力分布，从而改变叶轮的径向力。从图9可看出，含气量为10%时，流量减少及含气量对动态循环分量的影响导致叶轮的径向力分布非常不均匀。这主要由两方面原因造成：1) 断电停机工况下，泵体内介质流速减慢的同时叶轮出口处流速却增加，导致从叶轮内流出的介质不能平顺地与泵体内介质相汇合，而是撞击在泵体内的介质上，撞击的结果使流出叶轮介质的流速下降，与泵体内的流速相同，同时，部分动能通过撞击传给泵体内的介质，使得泵体内介质的压力增高；2) 由于气相在核主泵的各水力部件(叶轮、导叶、泵体)内的分布并不均匀，导致每个水力部件内均存在较大的动态循环分量，严重影响核主泵叶轮的径向力。最大不平衡径向力有正有负，随着含气量的增加，叶轮内的气体体积分数急剧增加而近乎完全被气相所占据，故叶轮内径向力的不平衡程度开始减弱，叶轮最大不平衡径向力变为以负值为主。

含气量：a——10%；b——20%；c——30%

2.5 叶轮流道内气体体积分数的变化

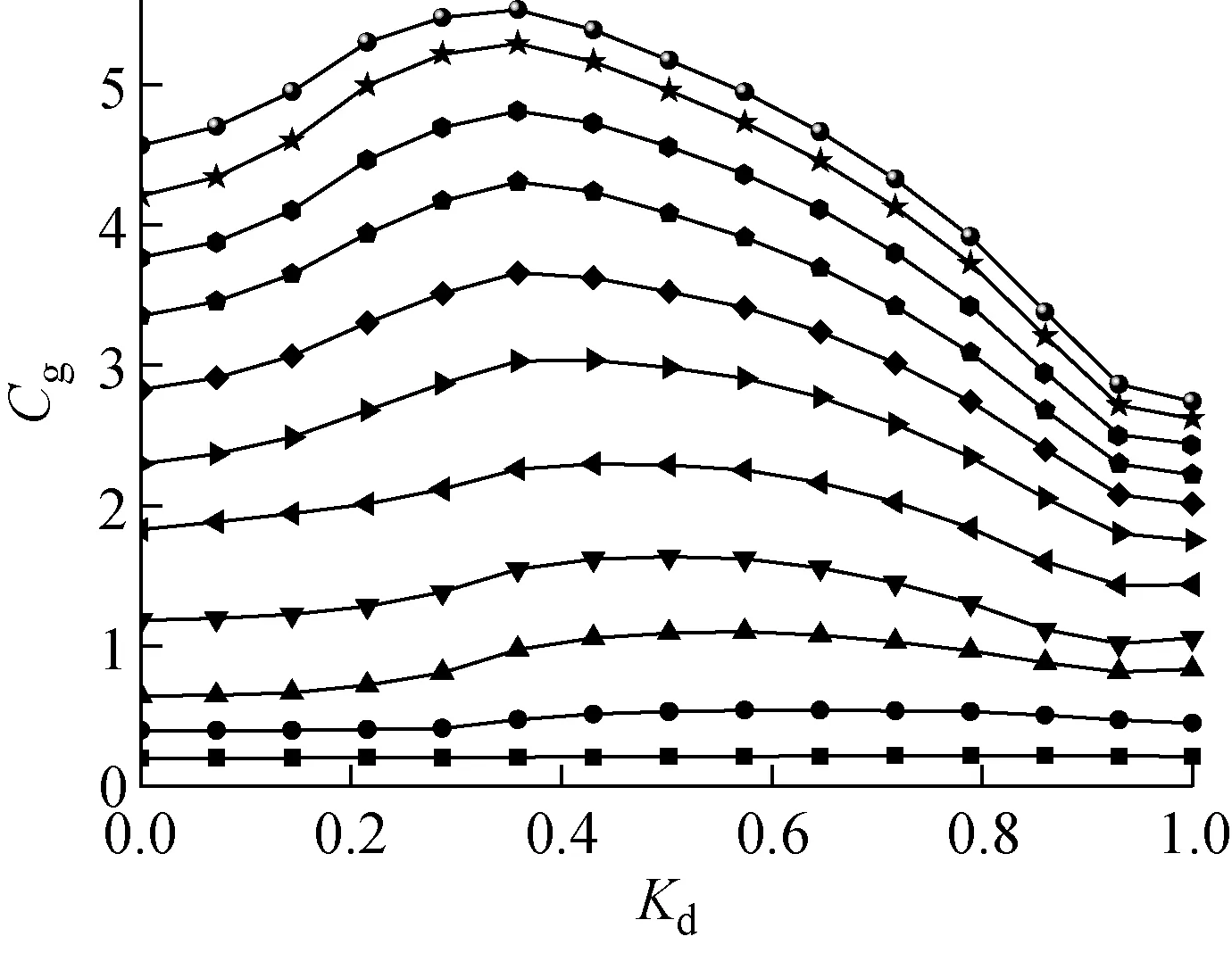
图10示出叶轮进口至出口(从左到右)间的气体体积分数Cg随相对位置Kd和时间t/T的变化。从图10可看出，在t/T=0时，气体体积分数无明显变化。随着时间的增加，气体体积分数增大。在t/T=0.5之前，气体体积分数的变化梯度随时间的增加而增大；在t/T=0.5之后，其变化梯度随时间的增加而减小。在气体体积分数增大的过程中，其出现的位置也开始向进口方向移动。

2.6 试验验证

为验证断电停机过渡过程中不同含气量对核主泵内部流动特性的影响，按照相似换算法将原机进行缩小并制造成样机在闭式试验台上进行试验。不同含气量时流量-扬程曲线的测量和数值模拟结果示于图11。由图11可见：相同含气量时，随着流量的减少，相对应的扬程有所下降；不同含气量所对应的流量-扬程曲线不同，含气量越大对应的流量-扬程曲线峰值越小。由图11还可见，试验结果与数值模拟结果相差不大，故建立的数值模型和计算方法可信，可用数值模拟方法对核主泵断电停机过渡过程进行气液两相瞬态流动特性分析。

从下至上，t/T分别为0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1

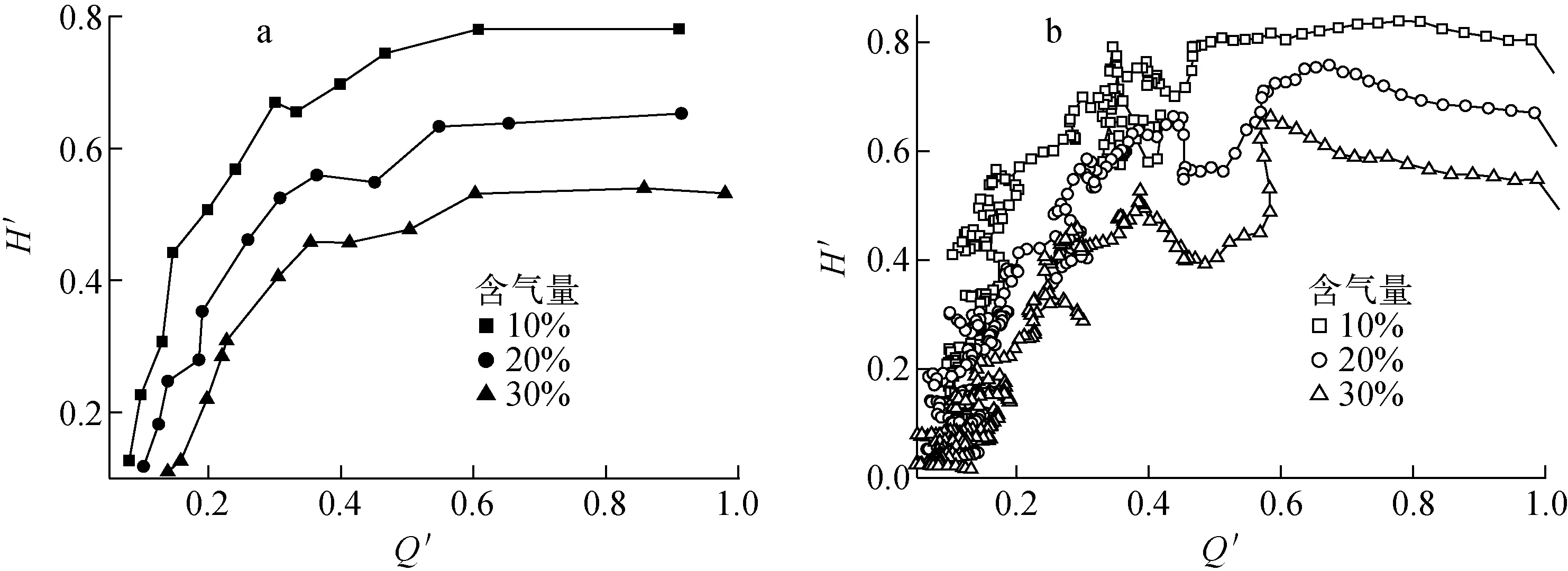
a——试验结果；b——数值模拟结果

3 结论

1) 在断电停机过渡过程中，叶轮背面附近产生旋涡，旋涡的存在使气相区域变大且相应的气体体积分数增加。随着流量的减少和转速的降低，叶轮进行转换能量的能力减弱，导致叶轮和导叶内存在大量的气相，而泵体内的气体体积分数分布由内向外逐渐增大。

2) 不同含气量对应叶轮内气体体积分数的变化不同。含气量为10%和20%时叶轮内气体体积分数先达到最大值后开始呈离散状回旋下降。而含气量为30%时，叶轮内的气体体积分数随流量的减少而增加，并未出现下降趋势，仅在小流量工况下出现回旋波动。

3) 含气量为10%时，由于叶轮出口附近出现旋涡影响其出口处的流速，旋涡向叶轮进口方向移动进而影响整个叶轮流速的变化。含气量为20%时，不仅叶轮出口处的流速受旋涡影响出现急剧波动，靠近叶片进口处受气相的影响也开始出现急剧波动。当含气量增加至30%时，叶轮流道内的流速在含气量为20%的基础上发生不同程度的变化。故在断电停机过渡过程中，含气量的变化对叶轮流道内的流速影响较大。

4) 含气量对动态循环分量的影响导致叶轮径向力的变化非常不均匀。随着含气量的增加，由于叶轮内的气体体积分数急剧增加而近乎完全被气相所占据，故叶轮的径向力不平衡程度开始减弱，其最大不平衡径向力由正负值不等转变为以负值为主。

参考文献：

[1] ORNAHEN P, GUBINA F. Simulations and field tests of a reactor coolant pump emergency start-up by means of remote gas units[J]. Transactions on Energy Conversion, 1992, 7(4): 691-697.

[2] GAO Hong, GAO Feng. Transient flow analysis in reactor coolant pump systems during flow coastdown period[J]. Nuclear Engineering and Design, 2011, 241(2): 509-514.

[3] 刘夏杰，刘军生，王德忠，等. 断电事故对核主泵安全特性影响的试验研究[J]. 原子能科学技术，2009，43(5)：448-451.

LIU Xiajie, LIU Junsheng, WANG Dezhong, et al. Test study on safety features of station blackout accident for nuclear main pump[J]. Atomic Energy Science and Technology, 2009, 43(5): 448-451(in Chinese).

[4] ARAYA F. Transient analysis for design of primary coolant pump adopted to passive safety reactor JPSR[J]. Journal of Nuclear Science and Technology, 1995, 32(10): 1 039-1 046.

[5] TSUKAMOTO H, OHASHI H. Transient characteristics of a centrifugal pump during starting period[J]. ASME Journal of Fluid Engineering, 1982, 104(1): 6-13.

[6] TSUKAMOTO H, MATSUNAGA S, YONEDA H, et al. Transient characteristics of a centrifugal pump during stopping period[J]. ASME Journal of Fluid Engineering, 1986, 108(4): 392-399.

[7] LEFEBVRE P, BARKER W. Centrifugal pump performance during transient operation[J]. ASME Journal of Fluid Engineering, 1995, 117(2): 123-128.

[8] 傅天清，刘云芳，阎庆绂. 带负荷启动工况下泵系统的瞬变特性研究[J]. 太原理工大学学报，2003，34(4)：443-446.

FU Tianqing, LIU Yunfang, YAN Qingfu. Study of transient characteristics in pump system when start with load[J]. Journal of Taiyuan University of Technology, 2003, 34(4): 443-446(in Chinese).

[9] 黎义斌，赵伟国，王秀勇，等. 离心泵变工况流场分析及数值模拟[J]. 兰州理工大学学报，2007，33(6)：43-46.

LI Yibin, ZHAO Weiguo, WANG Xiuyong, et al. Analysis and numeric simulation of off-design flow field in centrifugal pump[J]. Journal of Lanzhou University of Technology, 2007, 33(6): 43-46(in Chinese).

[10] 刘占生，刘全忠，王洪杰. 离心泵变工况流场及叶轮流体激振力研究[J]. 哈尔滨工程大学学报，2008，29(12)：1 304-1 308.

LIU Zhansheng, LIU Quanzhong, WANG Hongjie. Analysis of off-design flow fields in centrifugal pumps and hydrodynamic forces on impellers[J]. Journal of Harbin Engineering University, 2008, 29(12): 1 304-1 308(in Chinese).