严重事故IVR下反应堆压力容器耦合传热数值模拟分析

姚彦贵，施 杨，蒋 兴，贺寅彪

(上海核工程研究设计院，上海 200233)

先进轻水堆(即第三代)核电厂AP1000设计遵循“ALWR-URD”，提高了核电厂安全指标的要求，将堆芯熔化物堆内包容(IVR)作为重要的缓解严重事故的安全措施之一。IVR是当发生堆芯融化初期，冷却水通过RPV外的金属保温层底部的注入RPV和金属保温层之间通道内，冷却RPV外壁，通过沸腾换热带走RPV下封头内熔融物产生的衰变热，从而使熔融物包容在RPV内，起到缓解事故的作用。因此堆腔注水将RPV传递的热量充分带走，保持在水沸腾换热的临界热负荷以内，是保证RPV压力边界结构完整性的必要条件。而防止RPV随时间的蠕变失效则是保证RPV压力边界完整性的充要条件。RPV主要存在如下两个问题：1) 堆腔注水是否保证RPV的有效冷却与堆内熔融物热量释放；2) 是否能保证防止RPV的高温蠕变失效[1-5]。而开展严重事故IVR下RPV结构完整性分析的主要输入是RPV内外壁的温度分布和RPV壁发生熔融后的剩余壁厚。

近年来，Sehgal等[6-7]、美国SNL的Pilch等[8]、法国CEA的Devos等[9]对RPV进行了一系列的缩比实验研究。但缩比实验并不能完全模拟RPV内外的自然对流情况，且实验代价昂贵。德国Willschutz采用有限元方法对RPV进行温度场和应力场分析，并与FOREVER实验数据对比；但该计算基于给定RPV壁面边界条件进行，无法模拟RPV内外流体流动换热情况。本文采用流-固-热耦合的方式，对RPV内熔融物、RPV壁面及RPV外部气液两相流进行耦合数值分析，以获得耦合情况下的温度场、流场及RPV熔化情况，为RPV在IVR下的结构完整性分析提供重要依据。

1 数学物理模型

IVR-RPV耦合现象属于气液两相流-固体-熔融物耦合换热流动，在该过程中包含自然对流沸腾换热及固体熔化、局部熔融物冷凝等问题，为使计算可行，需进行相应的简化假设：1) RPV外部堆腔冷却水为核态沸腾；2) RPV内部熔融物为两层结构；3) 熔融物底层为氧化层，上层为金属层；4) 熔融物上部空间空气为理想气体；5) RPV内壁的熔融过程通过迭代计算完成，即第一步假设RPV壁厚完整情况下计算RPV的内壁温度分布，通过计算获得的内壁温度分布，判断如果大于RPV熔点温度，表示该部分已熔化，这样在第二步中重新建模，并将熔化的部分挖掉，这样反复迭代几次，直到RPV内壁温度低于熔点温度。

本文采用CFD通用商业软件STAR-CCM+进行耦合传热数值模拟计算，计算区域模型如图1所示，分析计算所需数学物理模型如下。

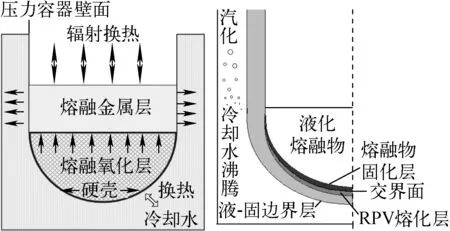
图1 模拟计算区域示意图

1.1 流体域控制方程

计算区域的流体域包括RPV外部两相流水隙、熔融物、RPV熔化层及熔融物顶部空气区域。流体域控制方程包含质量、动量、能量守恒方程：

ρα·(rαραUα

(1)

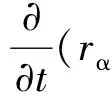
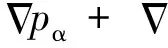
(2)

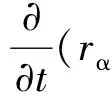
(3)

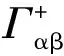
1.2 固体域控制方程

固体域导热方程如下：

λ

(4)

其中：cV为比定容热容；T为温度；t为时间；λ为导热系数。

1.3 相间动量交换模型

在气液两相流动过程中，任一α相会受到其他相作用力，包括相间拽力和相间非拽力，可表示为：

(5)

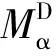
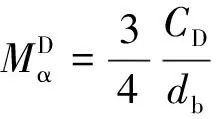
(6)

式中：db为气泡平均直径，m；CD取决于气泡雷诺数Reb，本文采用Ishii-Zuber[10]关系式计算；ρf为流体密度；Ug和Uf为气相和液相速度。

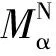
(7)

式中：FTD为湍流耗散力；CTD为湍流耗散力系数；Ccd为相间拽力动量传递系数，由Burns等[11]的经验关系式计算；vtc为修正系数；σtc为时间常数。

1.4 相间热量交换模型

相间传热采用双热阻模型，液相与界面间的传热为：

qls=hls(Ts-Tl)

(8)

其中：Ts为交界面温度；Tl为液相温度；hls为界面传热系数，采用Ranz-Marshall[12]经验关系式计算。

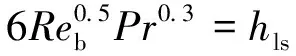
0≤Reb≤200

(9)

在气相侧，采用零热阻模型，其hα为无穷大，等效于交界面温度，即气相饱和温度。

1.5 相间质量交换模型

采用Rohsenow模型[13]计算蒸发率，沸腾壁面热流密度为：

(10)

其中：μl为液相动力黏度；hlat为汽化潜热；ρl、ρv分别为液相、气相密度；g为重力加速度；σ为表面张力；cpl为液相比定压热容；Tw、Tsat分别为壁面和饱和温度；Cqw为经验系数；Prl为液相普朗特数。

壁面核化点的蒸发率为：

(11)

其中，Cew为经验系数，表示壁面热流用于蒸发的份额。

2 网格划分及边界条件

2.1 网格划分

考虑到计算区域几何对称性，分析采用二维轴对称模型，为了模拟冷却水的自然循环，模型中建立水槽，并形成一定的水位，水位形成的压头为冷却水的入口压力，如图2所示。考察对象为RPV的熔化，因此对近壁面区域进行网格加密，对外水槽区域加粗。为了进行独立解验证，共采用3套网格划分方案，经独立解分析，确定最终选用的网格数量为64 023，网格示意图如图3所示。

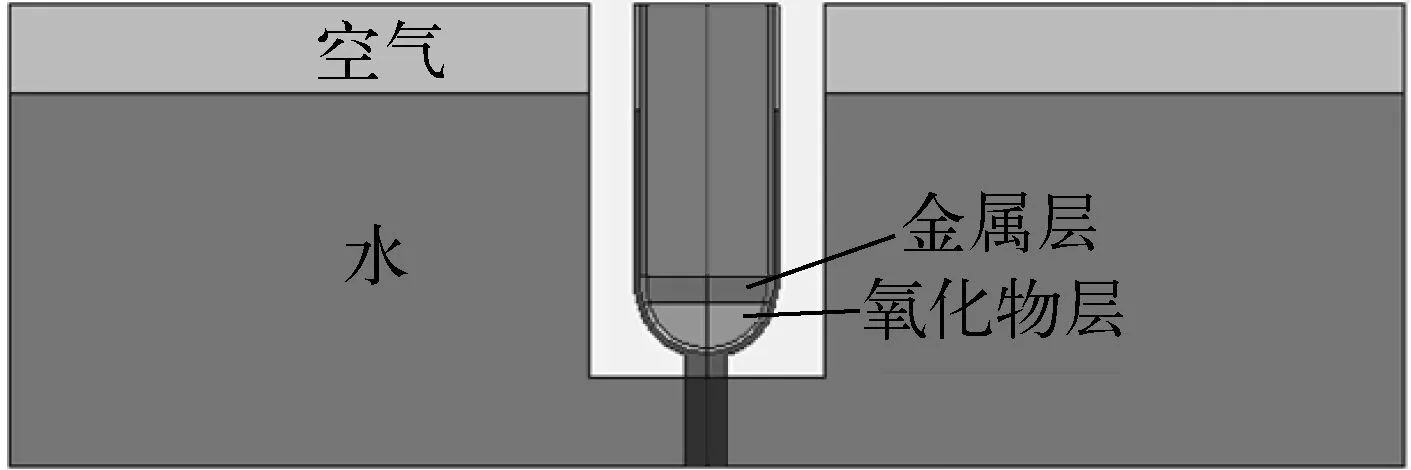
图2 分析模型

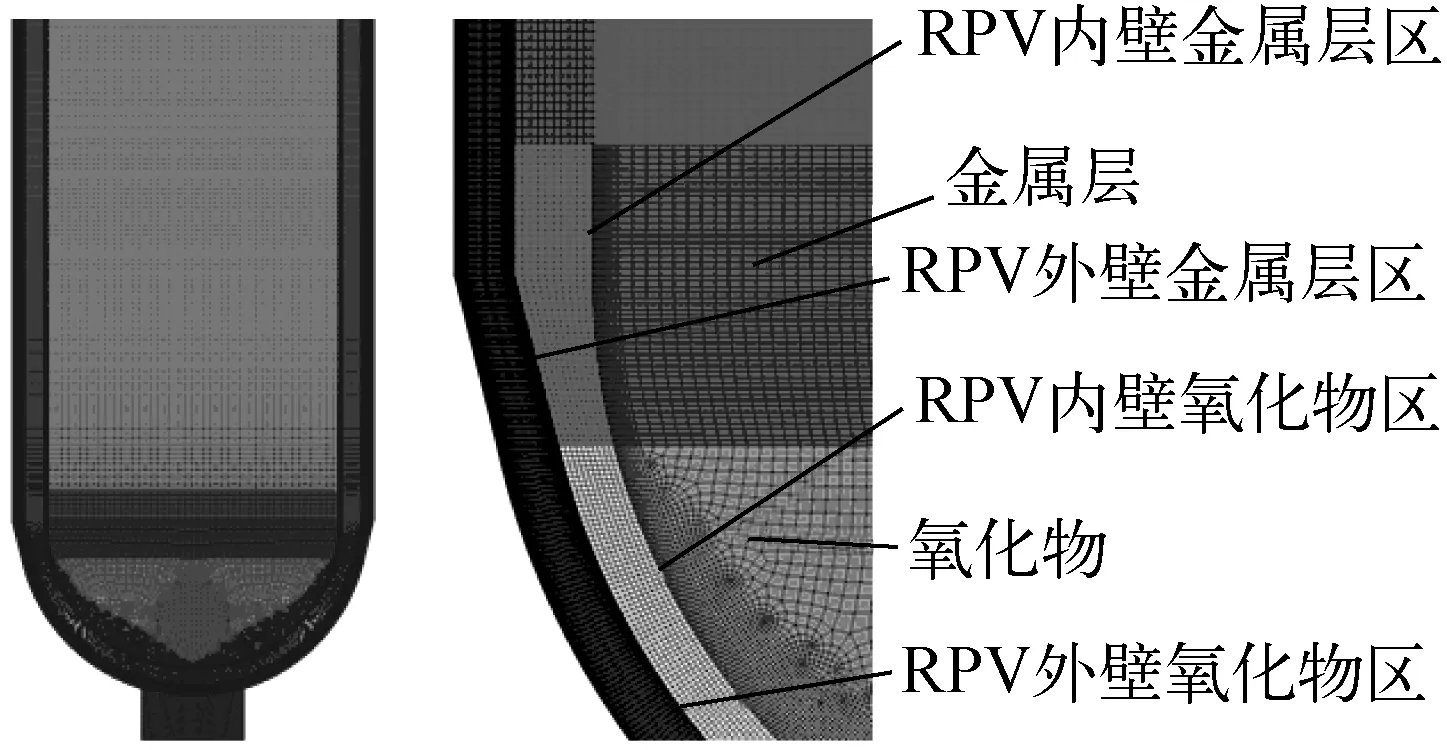
图3 分析模型网格示意图

2.2 边界条件

为确定偏微分方程的解，需设定合适的边界条件，本文依据物理背景，给定边界条件如下：

1) 气液两相流与外壁面边界：绝热、无滑移壁面；

2) 其他液体与固体交界面：热耦合无滑移壁面，热流密度由程序自动计算；

3) 氧化层：给定体积热源；

4) 水隙顶部边界：自由液面；

5) 金属层上表面：辐射换热；

6) 空气顶部边界：压力入口边界。

2.3 物理模型

计算所采用的物理模型有：1) 二维轴对称计算；2) 隐式非定常；3) 多相流模型，包括欧拉多相流模型、VOF方法和沸腾模型；4) 分离式求解；5) 重力模型；6) 湍流模型，即Realizable K-Epsilon模型。

计算需考虑VOF模型的沸腾模型，因此采用多相流的自由界面模型(VOF方法)，并考虑重力影响。同时本次VOF计算需采用非稳态计算，最终计算至液膜达到稳定。

2.4 介质物性

表1列出沸腾相关物性参数，表2列出凝固熔化相关物性参数。

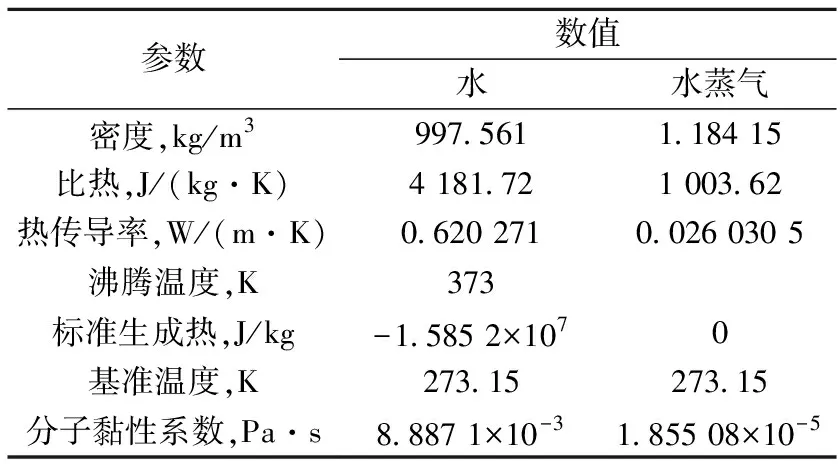
表1 沸腾相关物性参数

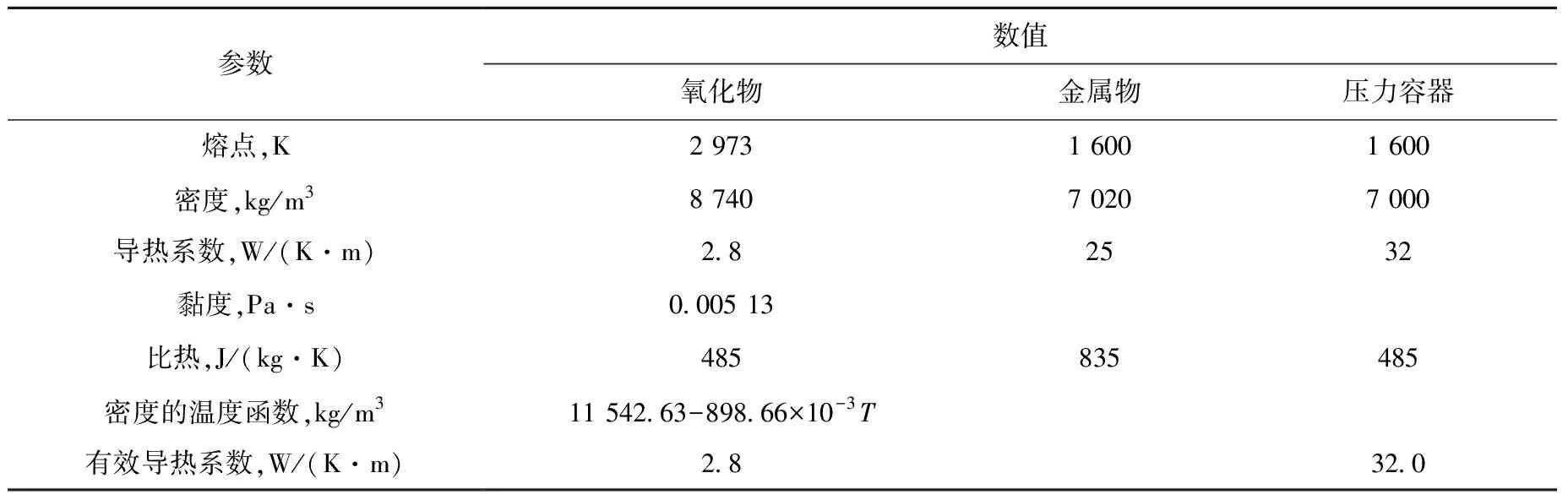
表2 凝固熔化相关物性参数

3 模拟结果与分析

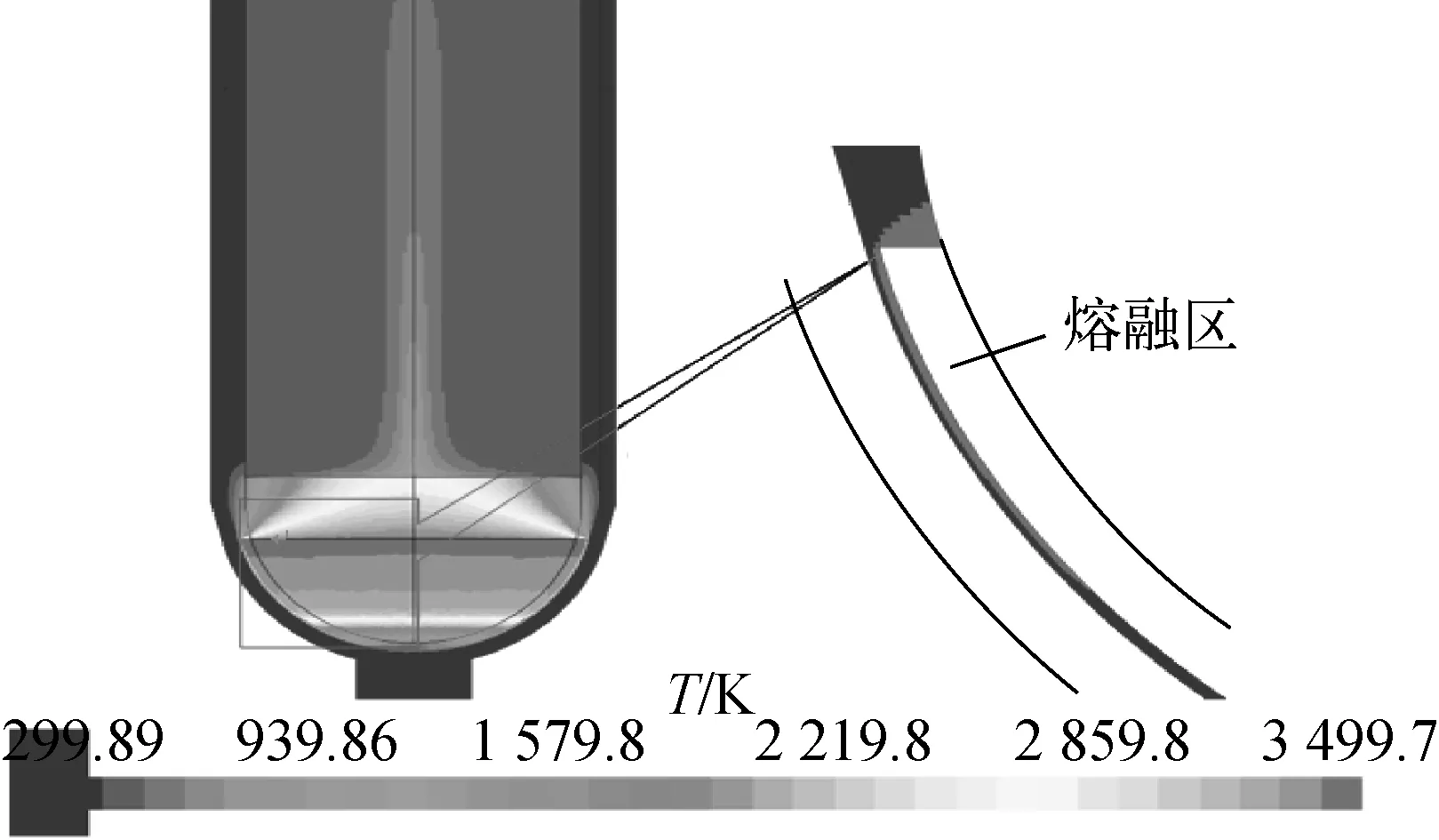
图4 温度分布

图4为温度分布云图，可见氧化物区域温度较高，且靠近金属层处温度最高，达到3 500 K左右，靠近底部温度逐渐降低，温度分布出现明显的热分层现象。右图为根据温度分布预测的RPV壁熔解区域，RPV壁材料为SA508 G3钢，其熔点为1 600 K，根据温度分布只要高于1 600 K就会熔解。从图中可知，靠近金属层处还会出现熔解现象，与金属层接触的只有靠近氧化物层的底部出现熔融现象。

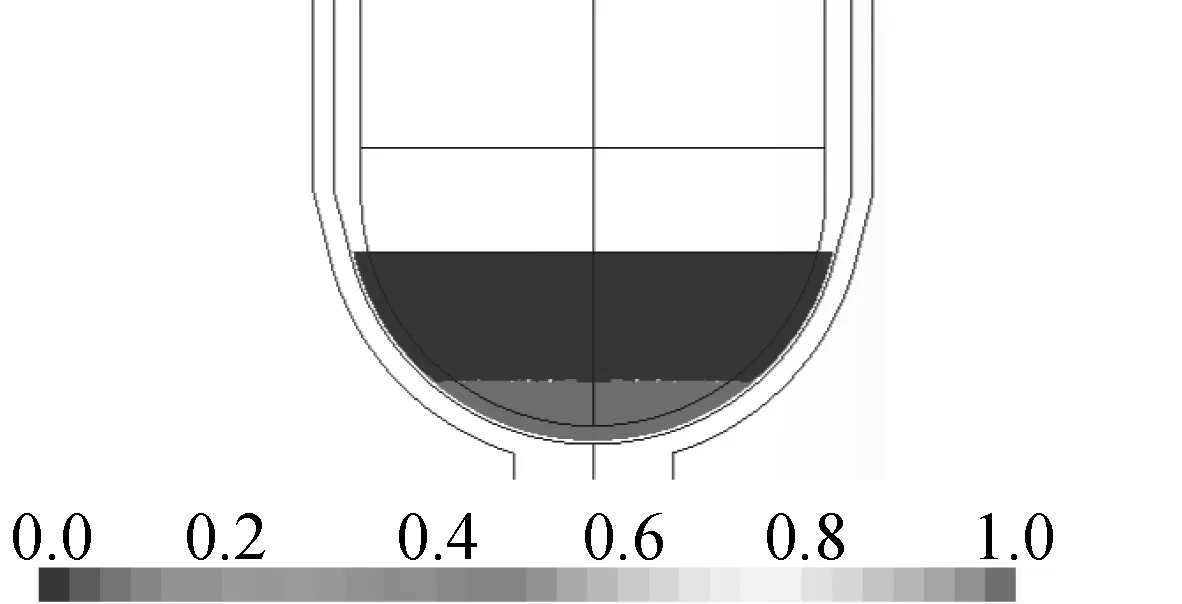
图5 固体体积分率分布

图5为熔融物区域固体体积份额分布，可看出，除底部出现大量凝固外，在RPV交界面上也有一薄层凝固层。这是因为在RPV内壁面上，虽然此时RPV被加热甚至熔化，但是该处温度仍远低于熔融物熔化温度(凝固温度)，由于热交换的作用，靠近RPV内壁面的熔融物温度降低到凝固点之下，从而产生一层凝固层。

图6为速度矢量分布，可知空气域存在由中心上升、壁面附近下降的自然对流，而沸腾域存在周期性运动，1个周期内存在向上或向下的运动。熔池内熔融物也发生自然对流，熔融物沿RPV内壁面向下流动。图7为底部水槽进口流量随时间的变化，可知进入沸腾区域的水发生周期性的变化，这主要是由于流道内两相流阻力的不稳定，与恒定的驱动压头之间的不断平衡造成的。

图6 速度矢量分布

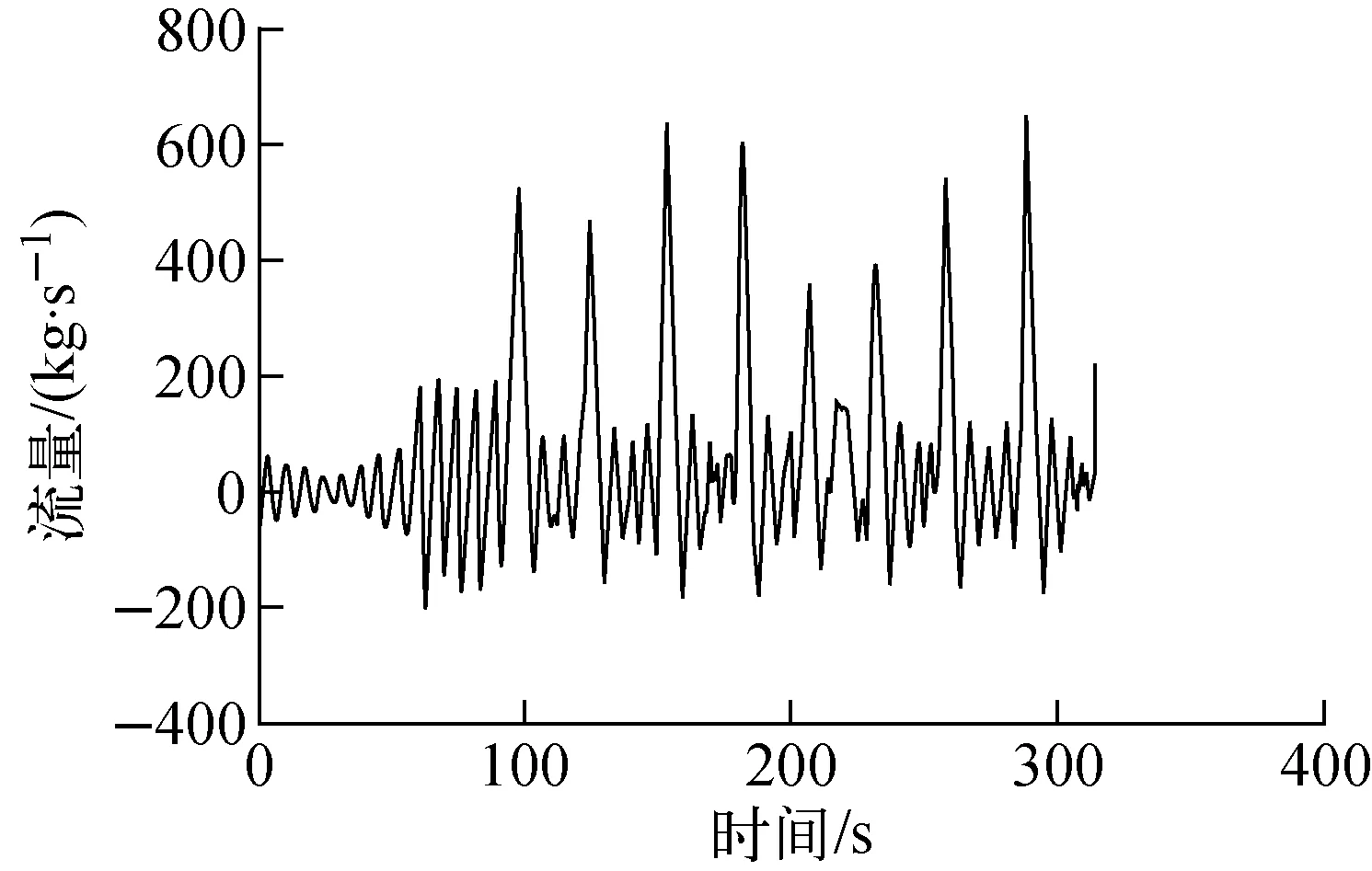
图7 进口水流量随时间的变化

图8为RPV内外壁面温度及热流密度分布，x坐标为中心轴向坐标，中心轴为从RPV底部到金属层上表面，模型中从RPV到金属层上表面共2.5 m。从图8可知，在氧化物层与RPV壁交界的中心高度热流密度出现峰值，且一直到金属层交界处，壁面热流密度达2 200 kW/m2，这也是金属层导热系数高的原因，因此氧化物层传给金属层的热迅速向RPV壁方向传递。从RPV内壁面温度分布可知，内壁面温度高于熔点，因此与氧化物层交界处发生熔融现象。

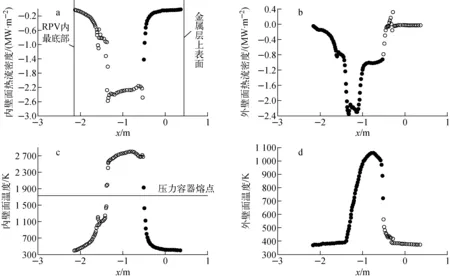
a,c:——RPV内壁氧化物区，——RPV内壁金属层区；b,d:——RPV外壁氧化物区，——RPV外壁金属层区

4 结论

本文采用大型CFD分析软件STAR-CCM+，对严重事故IVR下RPV内熔融物和堆外冷却水沸腾换热进行了耦合数值模拟分析，通过耦合分析模拟了严重事故下RPV的温度分布。为严重事故IVR下RPV结构完整性分析提供了依据，并得到以下结论：

1) IVR情况下，熔融物内部会形成热分层，在熔融物底部与RPV内壁面交界处发生凝固现象；

2) RPV外部的冷却水会形成波动性的气液两相流；

3) RPV内壁面部分材料被熔化，RPV壁面未被熔穿，仍保留一定的壁厚；

4) 在极限热源条件下，RPV熔融后壁厚最薄处达10 mm，壁面热流密度最高达2 200 kW/m2。

本文工作开展过程中得到了艾迪捷信息科技(上海)有限公司软件技术人员的大力支持，在此对李晶博士、江兴贤和韩海博士表示衷心的感谢。

参考文献：

[1] SEHGAL B R, THEERTHAN A, GIRI A, et al. Assessment of reactor vessel integrity (ARVI)[J]. Nuclear Engineering and Design, 2003, 221(1-3): 23-53.

[2] 姚伟达，谢永诚，贺寅彪，等. 第三代非能动型与第四代超临界先进轻水型核电厂中典型的力学问题[C]∥第14届全国反应堆结构力学会议论文集. 桂林：中国力学学会，2006.

[3] ASME boiler and pressure vessel code: Rules for construction of nuclear facility components[S]. New York, USA: ASME, 2004.

[4] 武志玮，宁冬，姚伟达. 严重事故下反应堆压力容器材料高温蠕变研究进展[J]. 核安全，2011(2)：20-24.

WU Zhiwei, NING Dong, YAO Weida. Research progress on high-temperature creep behavior of reactor pressure vessel[J]. Nuclear Safety, 2011(2): 20-24(in Chinese).

[5] 姚彦贵，宁冬，武志玮，等. 假想堆芯熔化严重事故下反应堆压力容器完整性的研究进展与建议[J]. 核技术，2013，36(4)：040615-1-040615-5.

YAO Yangui, NING Dong, WU Zhiwei, et al. Research progress and recommendations on reactor pressure vessel integrity under hypothetical core melt down accident[J]. Nuclear Techniques, 2013, 36(4): 040615-1-040615-5(in Chinese).

[6] SEHGAL B R, NOURGALIEV R R, DINH T N. Characterization of heat transfer processes in a melt pool convection and vessel-creep experiment[J]. Nuclear Engineering and Design, 2002, 211(2-3): 173-187.

[7] WILLSCHÜTZ H G, ALTSTADT E, SEHGAL B R, et al. Coupled thermal structural analysis of LWR vessel creep failure experiments[J]. Nuclear Engineering and Design, 2001, 208(3): 265-282.

[8] PILCH M M, LUDWIGSEN J S, CHU T Y, et al. Creep failure of a reactor pressure vessel lower head under severe accident conditions[C]∥ASME/JSME Joint Pressure Vessel and Piping (PVP) Conference. San Diego, CA: ASME, 1998.

[9] DEVOS J, SAINTE C C, POETTE C, et al. CEA programme to model the failure of the lower head in severe accidents[J]. Nuclear Engineering and Design, 1999, 191(1): 3-15.

[10] ISHII M, ZUBER N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows[J]. AIChE J, 1979, 25: 843-855.

[11] BURNS A D, FRANK T, HAMILL I, et al. The FAVRE averaged drag model for turbulent dispersion in Eulerian multi-phase flows[C]∥5th International Conference on Multiphase Flow, ICMF-2004. Yokohama, Japan: JSME, 2004.

[12] RANZ W E, MARSHALL W R. Evaporation form drops[J]. Chem Eng Prog, 1952, 48(3): 141-147.

[13] ROHSENOW W M. A method of correlation heat transfer data for surface boiling of liquid[J]. Trans ASME, 1952, 74: 969-978.