液体燃料熔盐堆三维稳态分析程序开发

周建军，张大林，秋穗正，苏光辉，田文喜，巫英伟

(西安交通大学 核科学与技术学院，陕西 西安 710049)

1 物理模型

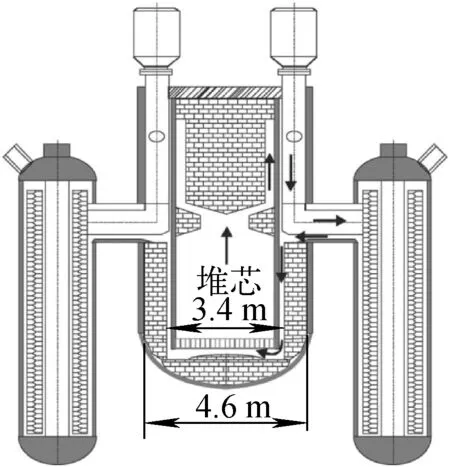
图1 MOSART堆芯结构

MOSART堆是一种先进的概念设计熔盐堆，它在放射性废物的有效焚化以及降解长寿命废料毒性和燃料闭式循环等方面均有很大的优势，最早由俄罗斯RRC-KI研究中心的Ignatiev等[7]提出。图1示出MOSART堆芯结构的概念设计。为了计算模拟的方便，本文将堆芯结构进行简化，仅考虑堆芯分流板以上到堆芯出口的部分，简化后的堆芯模型如图2所示，堆芯直径为1.9 m，在壁面附近有0.2 m厚的石墨反射层，采用锥形出口，燃料盐从下部进入，从上部流出，MOSART堆的主要熔盐物性和堆芯参数列于表1。

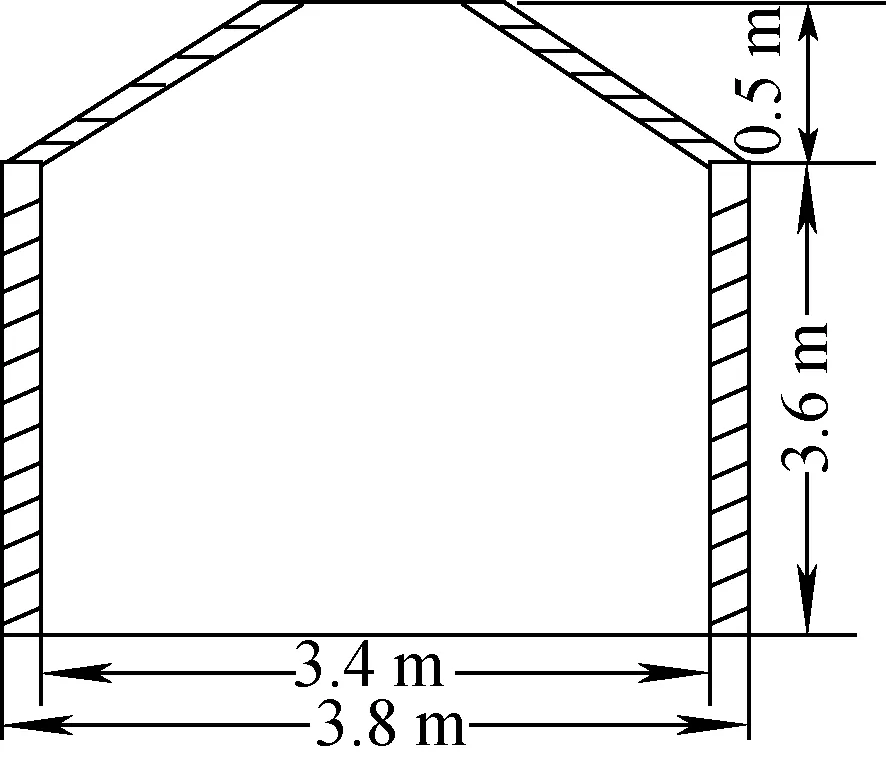
图2 堆芯结构

表1 MOSART堆芯初始设计参数

2 数学模型

2.1 中子物理模型

熔盐堆是一种液体反应堆，燃料盐溶解于氟化盐中在一回路循环，燃料处于流动状态。这与固体反应堆相比有很大差距，在进行物理计算时须考虑流动的影响。因此，为得到适用于液体堆的物理控制方程，本文从最原始的粒子守恒来进行推导，最终得到考虑了流动影响的中子扩散方程：

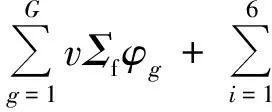
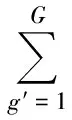
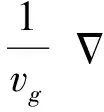
(1)

对于缓发中子先驱核同样可用这种方法得到，缓发中子先驱核守恒方程可表示为：

(2)

由于在石墨反射层中无流动特性和增殖特性。因此，可得到石墨反射层内的中子扩散方程和缓发中子方程：

(3)

Ci=0

(4)

式中：χp为瞬发中子能谱；χd为缓发中子能谱；φ为中子通量密度，cm-2·s-1；λ为缓发中子衰变常量，s-1；C为缓发中子先驱核浓度，cm-3；D为扩散系数，cm；Σf为宏观裂变截面，cm-1；Σs为宏观散射截面，cm-1；v为中子速度。其中，方程中的6群缓发中子份额和缓发中子衰变常量列于表2。

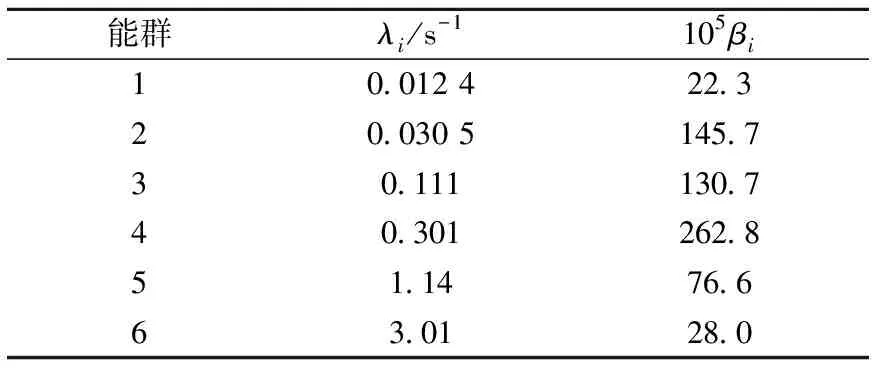
表2 缓发中子份额和衰变常量

2.2 流动和换热模型

稳态情况下熔盐在堆芯内的平均流速为0.5 m/s，文献[8]分析表明，稳态情况下堆芯内的Re将超过100 000，堆芯内的流动为湍流流动，本文选用标准k-ε湍流模型来模拟，控制方程如下。

质量守恒方程：

(5)

动量守恒方程：

μ

(6)

式中：uj为速度张量形式；Sui为广义源项的张量形式；μ为流体的动力黏性系数。

能量守恒方程：

(7)

式中，ST为源项，本文是堆芯的平均功率，包括快中子、慢中子及缓发中子产生的热量。

湍流控制方程：

(8)

式中：φ为广义变量，表示k或ε；Г为广义扩散系数；S为源项。对于k方程和ε方程，广义扩散系数可分别表示为：

Γk=η+ηt/σk

(9)

Γε=η+ηt/σε

(10)

式中：η为黏性系数；ηt为湍流黏性系数；湍流模型系数σk=1.0，σε=1.3。初始k可取初始动能的5%来计算，而ε可通过下式计算：

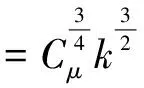
(11)

式中：Cμ为湍流模型中的经验系数，一般取0.09；l为湍流长度尺度。

3 数值计算方法

中子扩散方程、缓发中子先驱核方程和流动传热方程均可化为式(12)的模型方程，模型统一后各变量所对应的参数列于表3。

div(ρUφ)=div(Γgradφ)+S

(12)

需编制程序对方程进行数值求解。首先对方程进行离散，为保证方程的守恒性，采用有限容积积分法[9]对控制方程进行离散。图3为三维坐标网格系统下的控制容积P，对其积分可得到控制方程的离散方程。

有限容积法的三维计算控制容积如图3所示，对控制方程可采用控制容积积分法进行离散，三维坐标下的控制方程离散格式可写为：

表3 物理模型中的广义变量

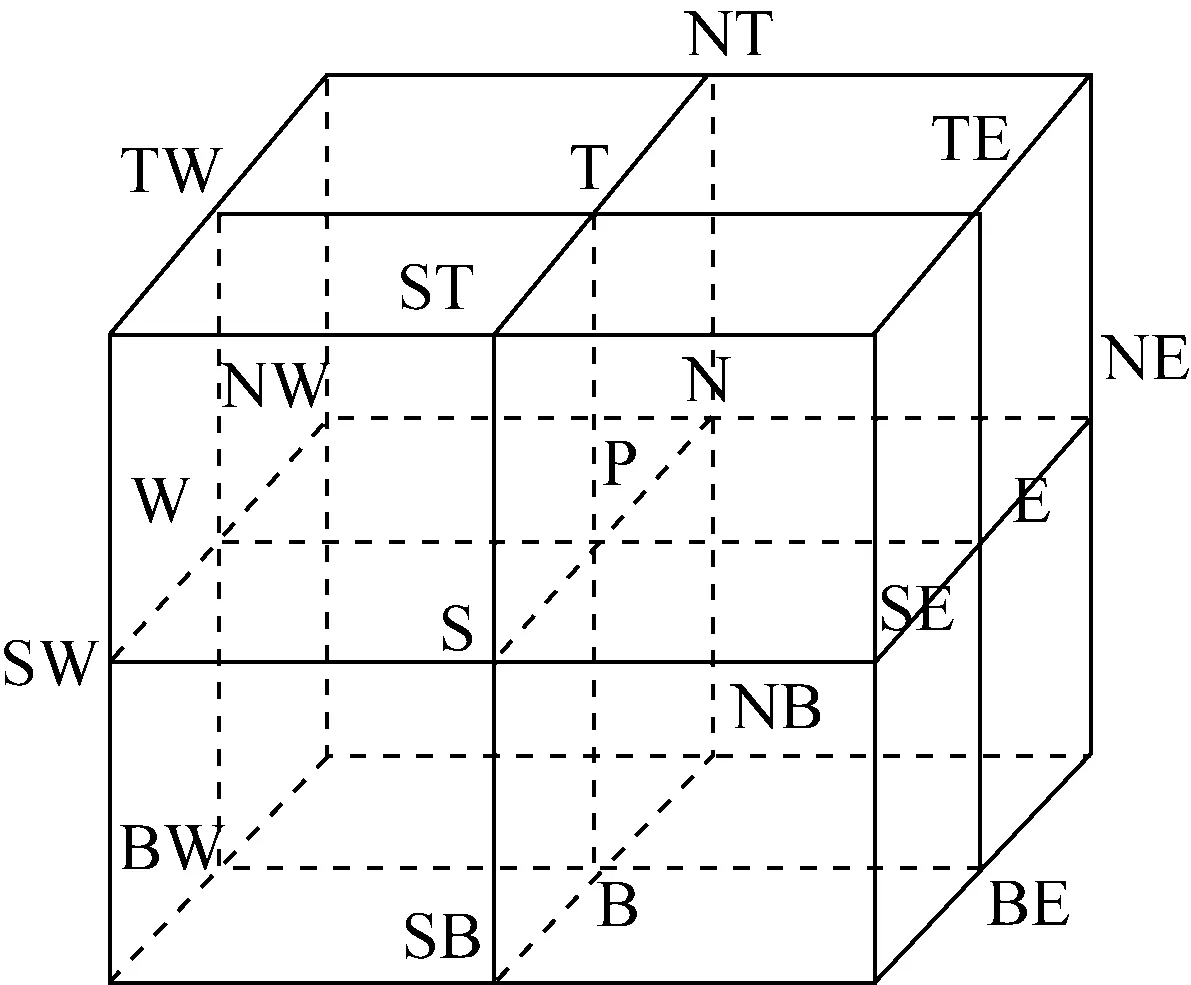
图3 控制容积

aPφP=aEφE+aWφW+aNφN+

aSφS+aBφB+aTφT+b

(13)

其中：

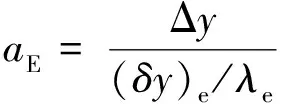
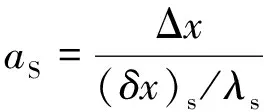
aP=aE+aW+aN+aS+aB+aT-SPΔV,

b=ScΔV

式中：下标W、S、E、N、B、T为节点；w、s、e、n、b、t为界面。

在离散方程中，界面上的当量扩散系数De、Dw、Dn、Ds、Db、Dt按调和平均计算。得到的方程组为5对角方程组，采用TDMA算法并辅以块修正方法求解。耦合计算流程示于图4。

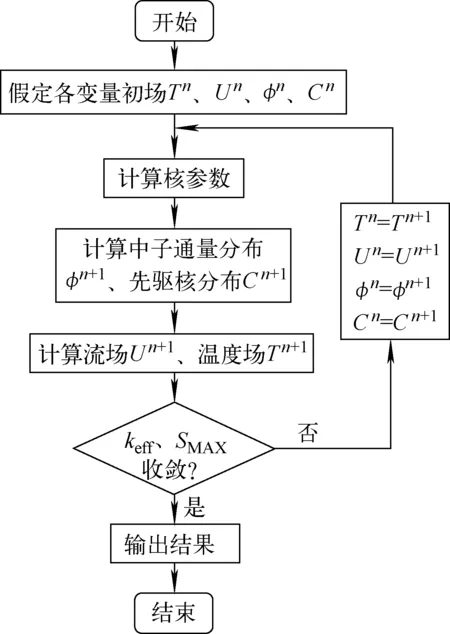
图4 耦合计算流程

4 程序验证及计算结果分析

4.1 程序验证

由于本文开发的是一三维物理热工耦合程序，而这种应用于熔盐堆的成熟的三维耦合程序和基准题尚很少见，但本文的程序既可考虑缓发和流动也可不考虑缓发和流动，因此对于程序的验证可从中子物理模型验证和流动传热模型验证分别进行。中子物理模型可用常见的三维基准题——Small LWR Core来验证[10]，计算结果列于表4，而对于流动传热模型可利用研究较多的三维自然对流模型来验证，计算值与实验值[11]的对比结果如图5所示。

表4 中子物理基准题验证结果

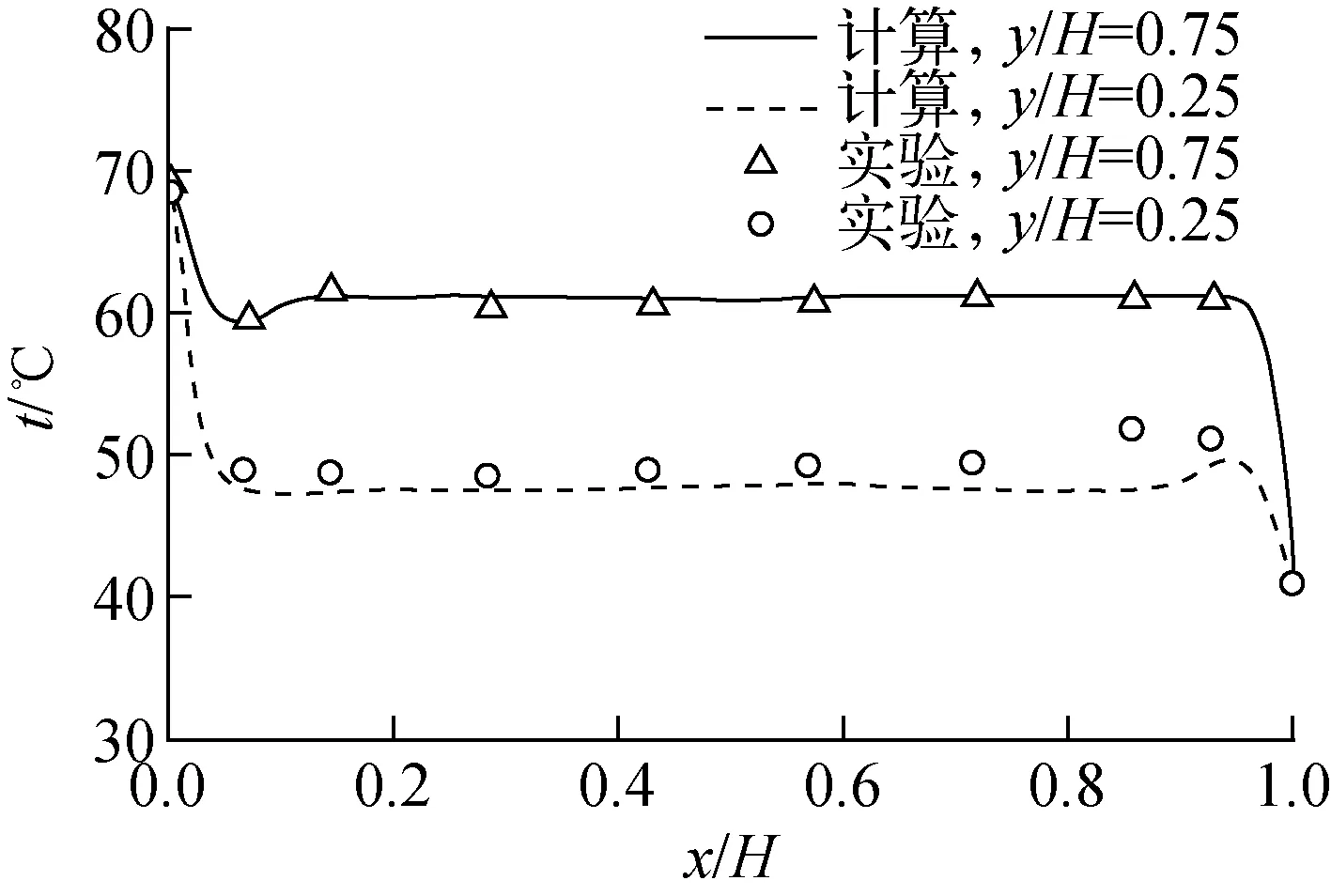
图5 温度随无量纲长度的分布

通过与三维基准题对比可发现，中子物理模型的计算结果与基准题的计算结果符合较好，证明了本文中采用的中子物理型的准确性。另外，通过计算三维自然对流并与文献中的实验结果进行对比发现，除个别点有一定的误差外，本文中的计算结果与实验值符合较好，这也证明了本文中采用的流动传热模型的准确性，从而也验证了开发的三维耦合程序的准确性。

4.2 计算结果分析

以快谱熔盐堆MOSART作为研究对象，分析了在稳态情况下入口速度效应对堆芯物理热工特性的影响，得到入口速度分别为0.1、0.4、0.5 m/s时的快中子分布、热中子分布、缓发中子分布及堆芯内的温度在高度方向的中截面沿径向分布。

1) 堆芯快中子

不同入口流速下快中子在堆芯高度方向中截面处沿径向分布曲线如图6所示。

图6 快中子分布

从图6可看出，作为一个均匀液体堆，MOSART堆的快中子通量密度在堆芯内的分布比较对称，最大值处于堆芯中心位置，流速对于快中子的分布影响不大。

2) 堆芯热中子

在不同入口速度下沿堆芯高度方向中截面处的热中子径向分布曲线如图7所示。由图7可见，热中子的分布在靠近堆芯壁面处有一增大的区域，这主要是因石墨反射层会使热中子裂变截面升高而造成的1个突变。通过对比快中子和慢中子的通量密度分布可看到，在本文研究的对象MOSART堆中快中子通量密度要较热中子通量密度高约1个数量级，因此，说明MOSART是1个快谱反应堆。且入口流速对于热中子在堆芯内部的分布影响也很小。

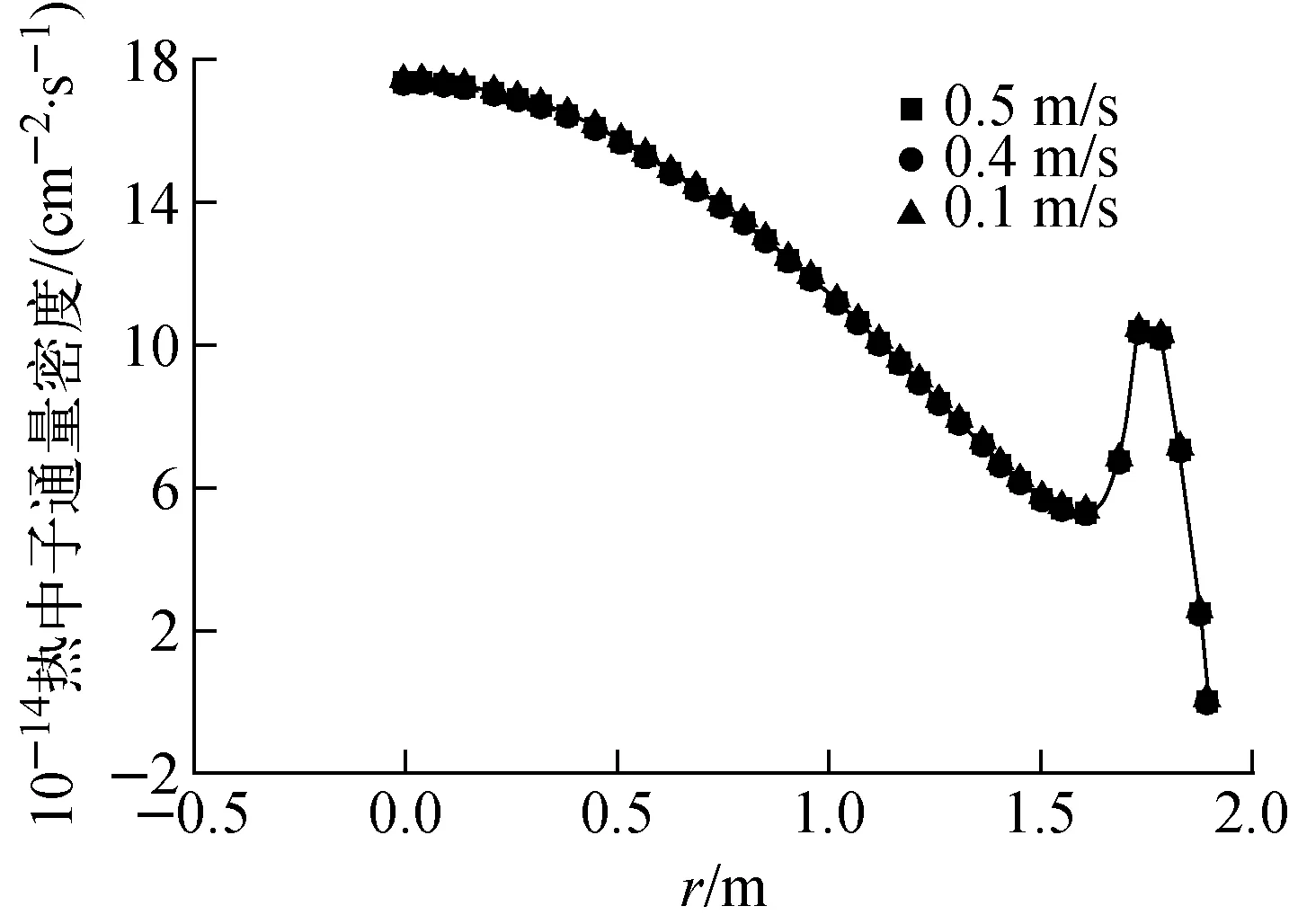
图7 热中子分布

3) 堆芯缓发中子先驱核

对于液体燃料熔盐反应堆，流动对缓发中子先驱核的分布有很大影响，因此研究不同流速下缓发中子先驱核的堆芯分布对分析堆芯物理特性是非常有意义的，在两种不同流速下6组缓发中子先驱核沿径向分布曲线如图8所示。

6组缓发中子先驱核分布表明，燃料盐的流动作用，使缓发中子先驱核沿流动方向整体向下游移动，峰值不像固体燃料反应堆中的会出现在堆芯的中心。缓发中子先驱核向下游移动的程度反映了流动对其影响程度，比较6组缓发中子先驱核浓度的分布可看出，缓发中子先驱核的衰变常量越小，流动对其影响越大。

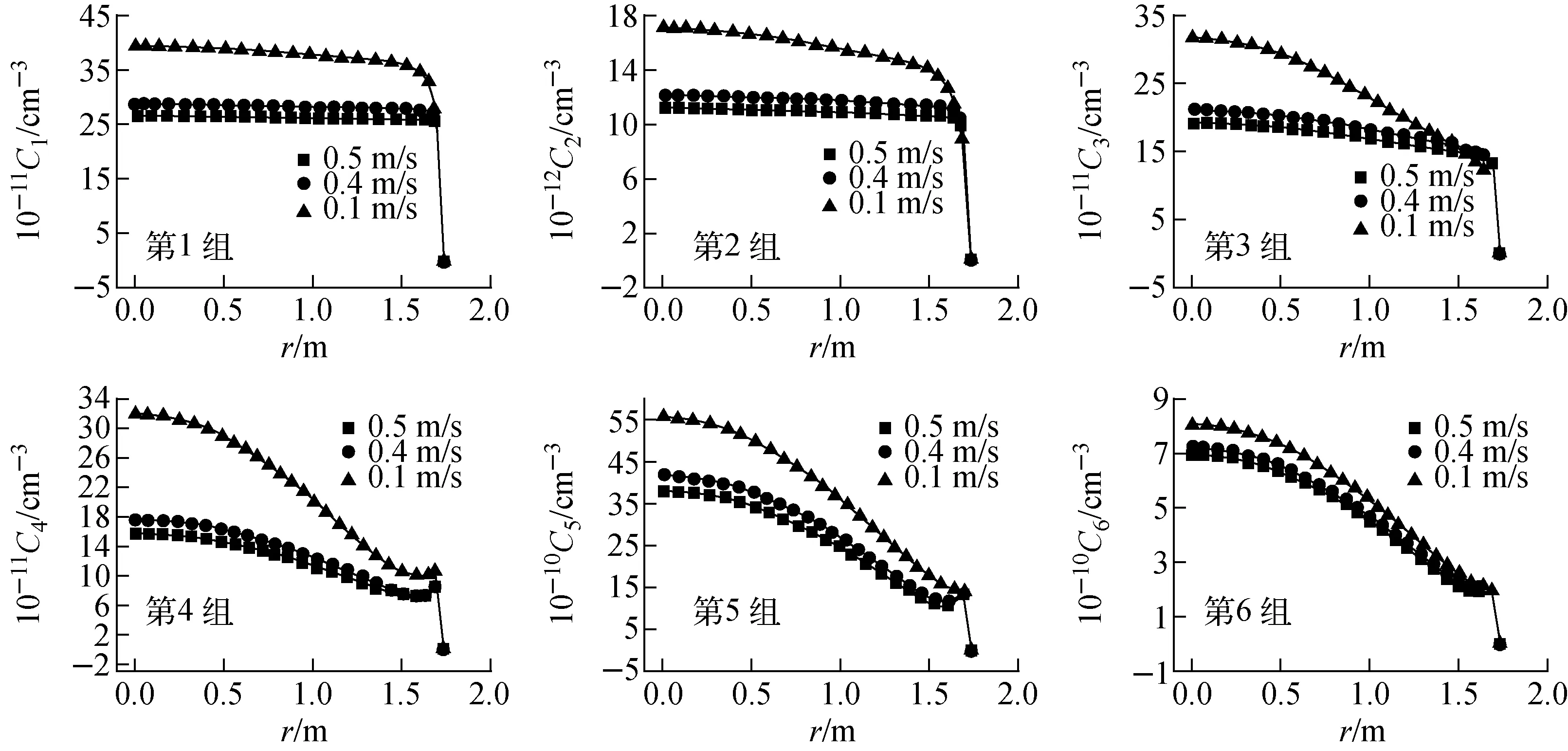
图8 缓发中子先驱核分布

4) 堆芯温度

当入口速度为0.1、0.4和0.5 m/s时，不同流速下堆芯内高度方向中截面沿轴向温度分布曲线如图9所示。

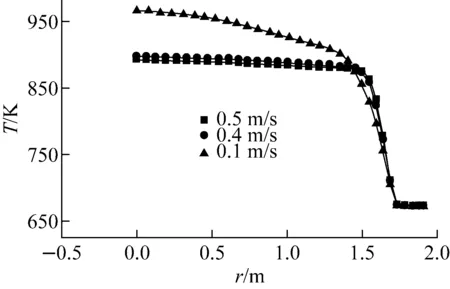
图9 温度分布

从图9可看出，流速对于堆芯内的温度分布影响较大，特别是在堆芯中间位置这种影响更明显，当流速较小时，堆芯中心线处的温度较其他区域的温度要高，但当流速较大时整个堆芯除了壁面附近的区域之外的其他区域温度分布相对比较均匀。

5 结论

本文以MOSART堆型作为研究对象，建立了适用于液体燃料熔盐反应堆的中子扩散方程，并结合流动传热方程，采用有限容积法对方程进行离散，编制了符合液体反应堆的三维耦合稳态分析程序，通过与中子物理和流动换热基准题的对比，验证了本程序的正确性。最后，利用本程序分析了MOSART堆芯的稳态特性，通过分析入口流速对堆芯物理热工特性的影响，可看出入口流速的变化对热中子和快中子的分布影响较小，而对于缓发中子的分布和堆芯内温度的分布影响较大。

参考文献：

[2] 张大林,秋穗正,刘长亮,等. 新概念熔盐堆堆芯稳态热工水力计算[J]. 工程热物理学报,2008,29(6):979-982.

ZHANG Dalin, QIU Suizheng, LIU Changliang, et al. Steady thermal-hydranlic analysis for the core of a new concept molten salt reactor[J]. Journal of Engineering Thermophysics, 2008, 29(6): 979-982(in Chinese).

[3] 张大林,秋穗正,刘长亮,等. 新概念熔盐堆物理计算方法研究及程序设计[J]. 原子能科学技术,2008,42(12):1 104-1 108.

ZHANG Dalin, QIU Suizheng, LIU Changliang, et al. Nuclear calculation and program development for moltensalt reactor[J]. At Energy Sci Technol, 2008, 42(12): 1 104-1 108(in Chinese).

[4] ZHANG D L, QIU S Z, SU G H, et al. Development of a steady state analysis code for a molten salt reactor[J]. Ann Nucl Energy, 2009, 36(5): 590-603.

[5] ZHANG D L, QIU S Z, SU G H, et al. Analysis on the neutron kinetics for a molten salt reactor[J]. Prog Nucl Energy, 2009, 51(4-5): 624-636.

[6] YAMAJI B, CSOM G, ASZDI A. Three-dimensional numerical investigation of a molten salt reactor concept with the code CFX-5.5[C]∥Nuclear Energy for New Europe 2002. Kranjska Gora: [s.n.], 2002.

[7] IGNATIEV V, FEYNBERG O, GNIDOI I, et al. Progress in development of Li, Be, Na/F molten salt actinide recycler & transmuter concept[C]∥Proceedings of ICAPP 2007. Nice, France: [s.n.], 2007.

[8] YAMAMOTO T, MITACHI K, SUZUKI T. Steady state analysis of small molten salt reactor: Effect of fuel salt flow on reactor characteristics[J]. JSME International Journal B: Fluids and Thermal Engineering, 2005, 48(3): 610-617.

[9] 陶文铨. 数值传热学[M]. 西安:西安交通大学出版社,2001.

[10] TAKEDA T, IKEDA H. 3D neutron transport benchmarks[J]. J Nucl Sci Technol, 1991, 28(7): 656-669.